Abstract
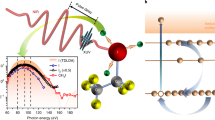
In photoelectron spectroscopy, the ionized electron wavefunction carries information about the structure of the bound orbital and the ionic potential as well as about the photoionization dynamics. However, retrieving the quantum phase information has been a long-standing challenge. Here, we transfer the electron phase retrieval problem into an optical one by measuring the time-reversed process of photoionization—photo-recombination—in attosecond pulse generation. We demonstrate all-optical interferometry of two independent phase-locked attosecond light sources. This measurement enables us to directly determine the phase shift associated with electron scattering in simple quantum systems such as helium and neon, over a large energy range. Moreover, the strong-field nature of attosecond pulse generation resolves the dipole phase around the Cooper minimum in argon through a single scattering angle. This method may enable the probing of complex orbital phases in molecular systems as well as electron correlations through resonances subject to strong laser fields.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Becker, U. Complete photoionisation experiments. J. Electron. Spectrosc. Relat. Phenom. 96, 105–115 (1998).
Motoki, S. et al. Complete photoionization experiment in the region of the 2σg → σu shape resonance of the N2 molecule. J. Phys. B 35, 3801–3819 (2002).
Marceau, C. et al. Molecular frame reconstruction using time-domain photoionization interferometry. Phys. Rev. Lett. 119, 083401 (2017).
Villeneuve, D. M., Hockett, P., Vrakking, M. J. J. & Niikura, H. Coherent imaging of an attosecond electron wave packet. Science 356, 1150–1153 (2017).
Paul, P. M. et al. Observation of a train of attosecond pulses from high harmonic generation. Science 292, 1689–1692 (2001).
Mairesse, Y. et al. Attosecond synchronization of high-harmonic soft X-rays. Science 302, 1540–1543 (2003).
Schultze, M. et al. Delay in photoemission. Science 328, 1658–1662 (2010).
Klünder, K. et al. Probing single-photon ionization on the attosecond time scale. Phys. Rev. Lett. 106, 143002 (2011).
Månsson, E. P. et al. Double ionization probed on the attosecond timescale. Nat. Phys. 10, 207–211 (2014).
Guénot, D. et al. Measurements of relative photoemission time delays in noble gas atoms. J. Phys. B 47, 245602 (2014).
Sabbar, M. et al. Resonance effects in photoemission time delays. Phys. Rev. Lett. 115, 133001 (2015).
Haessler, S. et al. Phase-resolved attosecond near-threshold photoionization of molecular nitrogen. Phys. Rev. A 80, 011404 (2009).
Cavalieri, A. L. et al. Attosecond spectroscopy in condensed matter. Nature 449, 1029–1032 (2007).
Wigner, E. P. Lower limit for the energy derivative of the scattering phase shift. Phys. Rev. 98, 145–147 (1955).
Dahlström, J. M., L'Huillier, A. & Maquet, A. Introduction to attosecond delays in photoionization. J. Phys. B 45, 183001 (2012).
Corkum, P. B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 71, 1994–1997 (1993).
Young, L. et al. X-ray microprobe of orbital alignment in strong-field ionized atoms. Phys. Rev. Lett. 97, 083601 (2006).
Hockett, P. Angle-resolved RABBITT: theory and numerics. J. Phys. B 50, 154002 (2017).
Shafir, D., Mairesse, Y., Villeneuve, D. M., Corkum, P. B. & Dudovich, N. Atomic wavefunctions probed through strong-field light–matter interaction. Nat. Phys. 5, 412–416 (2009).
Zerne, R. et al. Phase-locked high-order harmonic sources. Phys. Rev. Lett. 79, 1006–1009 (1997).
Kovačev, M. et al. Extreme ultraviolet Fourier-transform spectroscopy with high order harmonics. Phys. Rev. Lett. 95, 223903 (2005).
Corsi, C., Pirri, A., Sali, E., Tortora, A. & Bellini, M. Direct interferometric measurement of the atomic dipole phase in high-order harmonic generation. Phys. Rev. Lett. 97, 023901 (2006).
Bertrand, J. B., Wörner, H. J., Salières, P., Villeneuve, D. M. & Corkum, P. B. Linked attosecond phase interferometry for molecular frame measurements. Nat. Phys. 9, 174–178 (2013).
Kanai, T., Takahashi, E. J., Nabekawa, Y. & Midorikawa, K. Destructive interference during high harmonic generation in mixed gases. Phys. Rev. Lett. 98, 153904 (2007).
Jansen, G. S. M., Rudolf, D., Freisem, L., Eikema, K. S. E. & Witte, S. Spatially resolved Fourier transform spectroscopy in the extreme ultraviolet. Optica 3, 1122–1125 (2016).
Ott, C. et al. Reconstruction and control of a time-dependent two-electron wave packet. Nature 516, 374–378 (2014).
Lewenstein, M., Balcou, P., Ivanov, M. Y., L’Huillier, A. & Corkum, P. B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 49, 2117–2132 (1994).
Varjú, K. et al. Frequency chirp of harmonic and attosecond pulses. J. Mod. Opt. 52, 379–394 (2005).
Shafir, D. et al. Resolving the time when an electron exits a tunnelling barrier. Nature 485, 343–346 (2012).
Le, A.-T., Morishita, T. & Lin, C. D. Extraction of the species-dependent dipole amplitude and phase from high-order harmonic spectra in rare-gas atoms. Phys. Rev. A 78, 023814 (2008).
Jin, C., Le, A.-T. & Lin, C. D. Medium propagation effects in high-order harmonic generation of Ar and N2. Phys. Rev. A 83, 023411 (2011).
Frolov, M. V., Manakov, N. L., Sarantseva, T. S. & Starace, A. F. Analytic confirmation that the factorized formula for harmonic generation involves the exact photorecombination cross section. Phys. Rev. A 83, 043416 (2011).
Ammosov, M., Delone, N. & Krainov, V. Tunnel ionization of complex atoms and atomic ions in an electromagnetic field. Sov. Phys. JETP 64, 1191–1194 (1986).
Bransden, B. H. & Joachain, C. J. Physics of Atoms and Molecules 2nd edn (Prentice-Hall, Harlow, UK, 2003).
Fano, U. Propensity rules: an analytical approach. Phys. Rev. A. 32, 617–618 (1985).
Cooper, J. W. Photoionization from outer atomic subshells. A model study. Phys. Rev. 128, 681–693 (1962).
Wörner, H. J., Niikura, H., Bertrand, J. B., Corkum, P. B. & Villeneuve, D. M. Observation of electronic structure minima in high-harmonic generation. Phys. Rev. Lett. 102, 103901 (2009).
Higuet, J. et al. High-order harmonic spectroscopy of the Cooper minimum in argon: experimental and theoretical study. Phys. Rev. A 83, 053401 (2011).
Kheifets, A. S. Time delay in valence-shell photoionization of noble-gas atoms. Phys. Rev. A 87, 063404 (2013).
Schoun, S. B. et al. Attosecond pulse shaping around a Cooper minimum. Phys. Rev. Lett. 112, 153001 (2014).
Beutler, H. Über Absorptionsserien von Argon, Krypton und Xenon, zu Termen zwischen den beiden Ionisierungsgrenzen 2 P 3 2/0 und 2 P 1 2/0. Z. Phys. 93, 177–196 (1935).
Kotur, M. et al. Spectral phase measurement of a Fano resonance using tunable attosecond pulses. Nat. Commun. 7, 10566 (2016).
Cirelli, C. et al. Anisotropic photoemission time delays close to a Fano resonance. Nat. Commun. 9, 955 (2018).
Wang, H. et al. Attosecond time-resolved autoionization of argon. Phys. Rev. Lett. 105, 143002 (2010).
Kaldun, A. et al. Observing the ultrafast buildup of a Fano resonance in the time domain. Science 354, 738–741 (2016).
Langer, B. et al. Angular distribution of the Ne 2s → np autoionization resonances: experimental and theoretical study. J. Phys. B 30, 593–607 (1997).
Berrah, N. et al. Angular-distribution parameters and R-matrix calculations of Ar 3s−1→np resonances. J. Phys. B 29, 5351–5365 (1996).
X-ray Form Factor, Attenuation, and Scattering Tables (NIST, 2016); https://www.nist.gov/pml/x-ray-form-factor-attenuation-and-scattering-tables
Pabst, S. & Santra, R. Spin-orbit effects in atomic high-harmonic generation. J. Phys. B 47, 124026 (2014).
Torlina, L. & Smirnova, O. Coulomb time delays in high harmonic generation. New J. Phys. 19, 023012 (2017).
Schmidt, M. W. et al. General atomic and molecular electronic structure system. J. Comput. Chem. 14, 1347–1363 (1993).
Dunning, T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023 (1989).
Slater, J. C. & Johnson, K. H. Self-consistent-field xα cluster method for polyatomic molecules and solids. Phys. Rev. B 5, 844–853 (1972).
Schwarz, K. Optimization of the statistical exchange parameter σ for the free atoms H through Nb. Phys. Rev. B 5, 2466–2468 (1972).
Latter, R. Atomic energy levels for the Thomas-Fermi and Thomas-Fermi-Dirac potential. Phys. Rev. 99, 510–519 (1955).
Abramowitz, M. & Stegun, I. A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (US Government Printing Office, Washington, D.C., 1964).
Acknowledgements
We thank S. Patchkovskii, C. Ott and A. Harth for discussions. N.D. is the incumbent of the Robin Chemers Neustein Professorial Chair. N.D. acknowledges the Minerva Foundation, the Israeli Science Foundation, the Crown Center of Photonics and the European Research Council for financial support. M.K. acknowledges financial support by the Minerva Foundation and the Koshland Foundation. B.P., A.C., B.F. and Y.M. acknowledge financial support from the French National Research Agency through grant ANR-14-CE32-0014 MISFITS.
Author information
Authors and Affiliations
Contributions
N.D. and M.K. supervised the study. D.A. and M.K. designed and built the experimental setup. D.A., M.K. and O.K. carried out the measurements and analysed the data. B.P., A.C. and B.F. conceived and performed the theoretical calculations. D.A., M.K., N.D., B.P., B.F. and Y.M. interpreted the experimental and theoretical results. B.D.B. supported the operation of the laser system. All authors discussed the results and contributed to the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures.
Rights and permissions
About this article
Cite this article
Azoury, D., Kneller, O., Rozen, S. et al. Electronic wavefunctions probed by all-optical attosecond interferometry. Nature Photon 13, 54–59 (2019). https://doi.org/10.1038/s41566-018-0303-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-018-0303-4
This article is cited by
-
A look under the tunnelling barrier via attosecond-gated interferometry
Nature Photonics (2022)
-
Direct measurement of Coulomb-laser coupling
Scientific Reports (2021)
-
Spatial molecular interferometry via multidimensional high-harmonic spectroscopy
Nature Photonics (2020)