Abstract
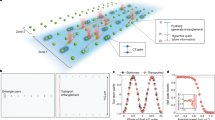
Quantum walks are powerful kernels in quantum computing protocols, and possess strong capabilities in speeding up various simulation and optimization tasks. One striking example is provided by quantum walkers evolving on glued trees1, which demonstrate faster hitting performances than classical random walks. However, their experimental implementation is challenging, as this involves highly complex arrangements of an exponentially increasing number of nodes. Here, we propose an alternative structure with a polynomially increasing number of nodes. We successfully map such graphs on quantum photonic chips using femtosecond-laser direct writing techniques in a geometrically scalable fashion. We experimentally demonstrate quantum fast hitting by implementing two-dimensional quantum walks on graphs with up to 160 nodes and a depth of eight layers, achieving a linear relationship between the optimal hitting time and the network depth. Our results open up a scalable path towards quantum speed-up in classically intractable complex problems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Childs, A. M., Farhi, E. & Gutmann, S. An example of the difference between quantum and classical random walks. Quantum Inf. Process. 1, 35–43 (2002).
Mohseni, M. et al. Commercialize quantum technologies in five years. Nature 543, 171–174 (2017).
Childs, A. M. & van Dam, W. Quantum algorithms for algebraic problems. Rev. Mod. Phys. 82, 1–52 (2008).
Szegedy, M. in Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science 32–41 (IEEE Computer Society, Washington, 2004).
Childs, A. M. & Goldstone, J. Spatial search by quantum walk. Phys. Rev. A 70, 022314 (2004).
Aaronson, S. & Shi, Y. Quantum lower bounds for the collision and the element distinctness problems. J. ACM 51, 595–605 (2004).
Buhrman, H. & Špalek, R. in Proceedings of the Seventeenth Annual ACM–SIAM Symposium on Discrete Algorithm 880–889 (SIAM, Philadelphia, 2006).
Farhi, E., Goldstone, J. & Gutmann, S. A quantum algorithm for the Hamiltonian NAND tree. Theory Comput. 4, 169–190 (2008).
Douglas, B. L. & Wang, J. B. A classical approach to the graph isomorphism problem using quantum walks. J. Phys. A 41, 075303 (2008).
Bruderer, M. & Plenio, M. B. Decoherence enhances performance of quantum walks applied to graph isomorphism testing. Phys. Rev. A 94, 062317 (2016).
Childs, A. M. et al. in Proceedings of the Thirty-fifth Annual ACM Symposium on Theory of Computing 59–68 (ACM, New York, 2003).
Farhi, E. & Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 58, 915–928 (1998).
Douglas, B. L. & Wang, J. B. Efficient quantum circuit implementation of quantum walks. Phys. Rev. A 79, 052335 (2009).
Carneiro, I. et al. Entanglement in coined quantum walks on regular graphs. New J. Phys. 7, 156 (2005).
Schmitz, H. et al. Quantum walk of a trapped ion in phase space. Phys. Rev. Lett. 103, 090504 (2009).
Karski, M. et al. Quantum walk in position space with single optically trapped atoms. Science 325, 174–177 (2009).
Broome, M. et al. Discrete single-photon quantum walks with tunable decoherence. Phys. Rev. Lett. 104, 153602 (2010).
Sansoni, L. et al. Two-particle bosonic-fermionic quantum walk via integrated photonics. Phys. Rev. Lett. 108, 010502 (2012).
Cardano, F. et al. Quantum walks and wavepacket dynamics on a lattice with twisted photons. Sci. Adv. 1, e1500087 (2015).
Du, J. et al. Experimental implementation of the quantum random-walk algorithm. Phys. Rev. A 67, 042316 (2003).
Perets, H. B. et al. Realization of quantum walks with negligible decoherence in waveguide lattices. Phys. Rev. Lett. 100, 170506 (2008).
Peruzzo, A. et al. Quantum walks of correlated photons. Science 329, 1500–1503 (2010).
Preiss, P. M. et al. Strongly correlated quantum walks in optical lattices. Science 347, 1229–1233 (2015).
Schreiber, A. et al. A 2D quantum walk simulation of two-particle dynamics. Science 336, 55–58 (2012).
Jeong, Y. C., Di Franco, C., Lim, H. T., Kim, M. S. & Kim, Y. H. Experimental realization of a delayed-choice quantum walk. Nat. Commun. 4, 2471 (2013).
Tang, H. et al. Experimental two-dimensional quantum walk on a photonic chip. Sci. Adv. 4, eaat3174 (2018).
Gao, J. et al. Non-classical photon correlation in a two-dimensional photonic lattice. Opt. Express 24, 12607–12616 (2016).
Szameit, A., Dreisow, F., Pertsch, T., Nolte, S. & Tünnermann, A. Control of directional evanescent coupling in fs laser written waveguides. Opt. Express 15, 1579–1587 (2007).
Izaac, J. A. & Wang, J. B. pyctqw: a continuous-time quantum walk simulator on distributed memory computers. Comput. Phys. Commun. 186, 81–92 (2015).
Whitfield, J. D., Rodríguez-Rosario, C. A. & Aspuru-Guzik, A. Quantum stochastic walks: a generalization of classical random walks and quantum walks. Phys. Rev. A 81, 022323 (2010).
Sánchez-Burillo, E., Duch, J., Gómez-Gardenes, J. & Zueco, D. Quantum navigation and ranking in complex networks. Sci. Rep. 2, 605 (2012).
Crespi, A. et al. Integrated multimode interferometers with arbitrary designs for photonic boson sampling. Nat. Photon. 7, 545–549 (2013).
Chaboyer, Z., Meany, T., Helt, L. G., Withford, M. J. & Steel, M. J. Tunable quantum interference in a 3D integrated circuit. Sci. Rep. 5, 9601 (2015).
Feng, Z. et al. Invisibility cloak printed on a photonic chip. Sci. Rep. 6, 28527 (2016).
Darázs, Z., Anishchenko, A., Kiss, T., Blumen, A. & Mülken, O. Transport properties of continuous-time quantum walks on sierpinski fractals. Phys. Rev. E 90, 032113 (2014).
Kim, Y. H. Quantum interference with beamlike type-II spontaneous parametric down-conversion. Phys. Rev. A 68, 013804 (2003).
Sun, K. et al. Mapping and measuring large-scale photonic correlation with single-photon imaging. Preprint at https://arxiv.org/abs/1806.09569 (2018).
Acknowledgements
The authors thank J. D. Whitfield for a very useful conversation on numerical methods for the quantum stochastic walks, and J.-W. Pan for helpful discussions. This research is supported by the National Key R&D Program of China (2017YFA0303700), the National Natural Science Foundation of China (11690033, 61734005, 11761141014, 11374211), the Science and Technology Commission of Shanghai Municipality (STCSM) (15QA1402200, 16JC1400405, 17JC1400403), Shanghai Municipal Education Commission (SMEC) (16SG09, 2017-01-07-00-02-E00049) and the open fund from the State Key Laboratory of High Performance Computing (HPCL) (no. 201511-01). C.D.F. is funded by the Singapore National Research Foundation (Fellowship NRF-NRFF2016-02). M.S.K. is supported by the Samsung Global Research Outreach (GRO) project, the Korea Institute of Science and Technology (KIST) Institutional Program (2E26680-18-P025), the Engineering and Physical Sciences Research Council (EPSRC) (EP/K034480/1) and the Royal Society. X.-M.J. acknowledges support from the National Young 1000 Talents Plan.
Author information
Authors and Affiliations
Contributions
X.-M.J. and M.S.K. conceived and supervised the project. H.T. and X.-M.J. designed the experiment. C.D.F., M.S.K. and T.-S.H. conducted the theoretical work. H.T., Z.-Y.S., J.G., K.S., Z.-Q.J. and X.-M.J. performed the single-photon experiment. H.T., Z.-M.L. and T.-Y.W. analysed the experimental data. Z.F. and Z.-Y.S. conducted chip fabrication. H.T., C.D.F., M.S.K. and X.-M.J. wrote the paper, with input from all the other authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures.
Supplementary Video 1
Quantum fast hitting dynamics.
Rights and permissions
About this article
Cite this article
Tang, H., Di Franco, C., Shi, ZY. et al. Experimental quantum fast hitting on hexagonal graphs. Nature Photon 12, 754–758 (2018). https://doi.org/10.1038/s41566-018-0282-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-018-0282-5
This article is cited by
-
High-efficiency reinforcement learning with hybrid architecture photonic integrated circuit
Nature Communications (2024)
-
Simulating photosynthetic energy transport on a photonic network
npj Quantum Information (2024)
-
A von-Neumann-like photonic processor and its application in studying quantum signature of chaos
Light: Science & Applications (2024)
-
Integrated photonics in quantum technologies
La Rivista del Nuovo Cimento (2023)
-
λ/30 inorganic features achieved by multi-photon 3D lithography
Nature Communications (2022)