Abstract
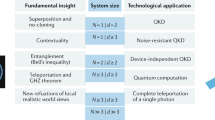
Quantum entanglement is important for emerging quantum technologies such as quantum computation and secure quantum networks. To boost these technologies, a race is currently ongoing to increase the number of particles in multiparticle entangled states, such as Greenberger–Horne–Zeilinger (GHZ) states. An alternative route is to increase the number of entangled quantum levels. Here, we overcome present experimental and technological challenges to create a three-particle GHZ state entangled in three levels for every particle. The resulting qutrit-entangled states are able to carry more information than entangled states of qubits. Our method, inspired by the computer algorithm Melvin, relies on a new multi-port that coherently manipulates several photons simultaneously in higher dimensions. The realization required us to develop a new high-brightness four-photon source entangled in orbital angular momentum. Our results allow qualitatively new refutations of local-realistic world views. We also expect that they will open up pathways for a further boost to quantum technologies.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Shor, P. W. Fault-tolerant quantum computation. In Proc. 37th Conf. Foundations of Computer Science 56–65 (IEEE, 1996).
Hillery, M., Bužek, V. & Berthiaume, A. Quantum secret sharing. Phys. Rev. A 59, 1829–1834 (1999).
Greenberger, D. M., Horne, M. A. & Zeilinger, A. in Bell’s Theorem, Quantum Theory and Conceptions of the Universe (ed. Kafatos, M.) 69–72 (Springer, The Netherlands, 1989).
Greenberger, D. M., Horne, M. A., Shimony, A. & Zeilinger, A. Bell’s theorem without inequalities. Am. J. Phys. 58, 1131–1143 (1990).
Krenn, M., Malik, M., Fickler, R., Lapkiewicz, R. & Zeilinger, A. Automated search for new quantum experiments. Phys. Rev. Lett. 116, 090405 (2016).
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Mermin, N. D. Extreme quantum entanglement in a superposition of macroscopically distinct states. Phys. Rev. Lett. 65, 1838–1840 (1990).
Monz, T. et al. 14-qubit entanglement: creation and coherence. Phys. Rev. Lett. 106, 130506 (2011).
Bouwmeester, D., Pan, J.-W., Daniell, M., Weinfurter, H. & Zeilinger, A. Observation of three-photon Greenberger–Horne–Zeilinger entanglement. Phys. Rev. Lett. 82, 1345–1349 (1999).
Pan, J.-W., Bouwmeester, D., Daniell, M., Weinfurter, H. & Zeilinger, A. Experimental test of quantum nonlocality in three-photon Greenberger–Horne–Zeilinger entanglement. Nature 403, 515 (2000).
Wang, X.-L. et al. Experimental ten-photon entanglement. Phys. Rev. Lett. 117, 210502 (2016).
Kelly, J. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66–69 (2015).
Song, C. et al. 10-qubit entanglement and parallel logic operations with a superconducting circuit. Phys. Rev. Lett. 119, 180511 (2017).
Pan, J.-W. et al. Multiphoton entanglement and interferometry. Rev. Mod. Phys. 84, 777–838 (2012).
Ryu, J., Lee, C., Żukowski, M. & Lee, J. Greenberger–Horne–Zeilinger theorem for N qudits. Phys. Rev. A 88, 042101 (2013).
Ryu, J. et al. Multisetting Greenberger–Horne–Zeilinger theorem. Phys. Rev. A 89, 024103 (2014).
Lawrence, J. Rotational covariance and Greenberger–Horne–Zeilinger theorems for three or more particles of any dimension. Phys. Rev. A 89, 012105 (2014).
Tang, W., Yu, S. & Oh, C. Multisetting Greenberger–Horne–Zeilinger paradoxes. Phys. Rev. A 95, 012131 (2017).
Malik, M. et al. Multi-photon entanglement in high dimensions. Nat. Photon. 10, 248–252 (2016).
Hiesmayr, B., De Dood, M. & Löffler, W. Observation of four-photon orbital angular momentum entanglement. Phys. Rev. Lett. 116, 073601 (2016).
Zhang, Y. et al. Simultaneous entanglement swapping of multiple orbital angular momentum states of light. Nat. Commun. 8, 632 (2017).
Krenn, M., Gu, X. & Zeilinger, A. Quantum experiments and graphs: multiparty states as coherent superpositions of perfect matchings. Phys. Rev. Lett. 119, 240403 (2017).
Gu, X., Erhard, M., Zeilinger, A. & Krenn, M. Quantum experiments and graphs II: computation and state generation with probabilistic sources and linear optics. Preprint at https://arxiv.org/abs/1803.10736 (2018).
Schlederer, F., Krenn, M., Fickler, R., Malik, M. & Zeilinger, A. Cyclic transformation of orbital angular momentum modes. New J. Phys. 18, 043019 (2016).
Babazadeh, A. et al. High-dimensional single-photon quantum gates: concepts and experiments. Phys. Rev. Lett. 119, 180510 (2017).
Krenn, M., Hochrainer, A., Lahiri, M. & Zeilinger, A. Entanglement by path identity. Phys. Rev. Lett. 118, 080401 (2017).
Allen, L., Beijersbergen, M. W., Spreeuw, R. & Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre–Gaussian laser modes. Phys. Rev. A 45, 8185 (1992).
Mair, A., Vaziri, A., Weihs, G. & Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313–316 (2001).
Yao, A. M. & Padgett, M. J. Orbital angular momentum: origins, behavior and applications. Adv. Opt. Photonics 3, 161–204 (2011).
Krenn, M., Malik, M., Erhard, M. & Zeilinger, A. Orbital angular momentum of photons and the entanglement of Laguerre–Gaussian modes. Philos. Trans. R. Soc. A 375, 20150442 (2017).
Hong, C., Ou, Z.-Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Zhang, Y. et al. Engineering two-photon high-dimensional states through quantum interference. Sci. Adv. 2, e1501165 (2016).
Miatto, F. et al. Bounds and optimisation of orbital angular momentum bandwidths within parametric downconversion systems. Eur. Phys. J. D 66, 1–6 (2012).
Leach, J., Padgett, M. J., Barnett, S. M., Franke-Arnold, S. & Courtial, J. Measuring the orbital angular momentum of a single photon. Phys. Rev. Lett. 88, 257901 (2002).
Erhard, M., Malik, M. & Zeilinger, A. A quantum router for high-dimensional entanglement. Quantum Sci. Technol. 2, 014001 (2017).
Huber, M. & de Vicente, J. I. Structure of multidimensional entanglement in multipartite systems. Phys. Rev. Lett. 110, 030501 (2013).
Bavaresco, J. et al. Measurements in two bases are sufficient for certifying high-dimensional entanglement. Nat. Phys. 14, 1032–1037 (2018).
Mirhosseini, M., Malik, M., Shi, Z. & Boyd, R. W. Efficient separation of the orbital angular momentum eigenstates of light. Nat. Commun. 4, 2781 (2013).
Lawrence, J. Mermin inequalities for perfect correlations in many-qutrit systems. Phys. Rev. A 95, 042123 (2017).
Graffitti, F., Kundys, D., Reid, D. T., Brańczyk, A. M. & Fedrizzi, A. Pure down-conversion photons through sub-coherence-length domain engineering. Quantum Sci. Technol. 2, 035001 (2017).
Barreiro, J. T., Wei, T.-C. & Kwiat, P. G. Beating the channel capacity limit for linear photonic superdense coding. Nat. Phys. 4, 282–286 (2008).
Sheridan, L. & Scarani, V. Security proof for quantum key distribution using qudit systems. Phys. Rev. A 82, 030301 (2010).
Bocharov, A., Roetteler, M. & Svore, K. M. Factoring with qutrits: Shor's algorithm on ternary and metaplectic quantum architectures. Phys. Rev. A 96, 012306 (2017).
Acknowledgements
We thank J. Lawrence, M. Huber, C. Brukner, A. Hochrainer, R. Fickler, T. Scheidl, F. Steinlechner and X. Gu for fruitful discussions. This work was supported by the Austrian Academy of Sciences (ÖAW), by the European Research Council (SIQS grant no. 600645 EU-FP7-ICT) and the Austrian Science Fund (FWF) with SFB F40 (FOQUS) and FWF project CoQuS no. W1210-N16. M.M. acknowledges support from the European Commission through a Marie Curie fellowship (OAMGHZ) and the joint Czech–Austrian project MultiQUEST (FWF I3053-N27), and the QuantERA ERA-NET Co-fund (FWF I3553-N36).
Author information
Authors and Affiliations
Contributions
The computer algorithm Melvin inspired an initial practical solution for the experiment. M.E. and M.M. performed the experiment. All authors analysed the data, discussed the results and wrote the manuscript. A.Z. initiated the research and supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures.
Rights and permissions
About this article
Cite this article
Erhard, M., Malik, M., Krenn, M. et al. Experimental Greenberger–Horne–Zeilinger entanglement beyond qubits. Nature Photon 12, 759–764 (2018). https://doi.org/10.1038/s41566-018-0257-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-018-0257-6
This article is cited by
-
Inverse design of high-dimensional quantum optical circuits in a complex medium
Nature Physics (2024)
-
Demonstration of hypergraph-state quantum information processing
Nature Communications (2024)
-
Demonstration of controlled high-dimensional quantum teleportation
Science China Physics, Mechanics & Astronomy (2024)
-
Quantum private comparison protocol via 4D layered states and DQC model
Quantum Information Processing (2024)
-
Classification of data with a qudit, a geometric approach
Quantum Machine Intelligence (2024)