Abstract
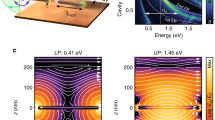
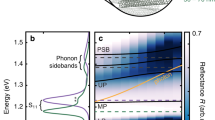
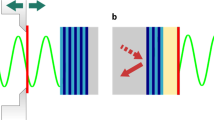
Non-perturbative coupling of photons and excitons produces hybrid particles, exciton–polaritons, which have exhibited a variety of many-body phenomena in various microcavity systems. However, the vacuum Rabi splitting (VRS), which defines the strength of photon–exciton coupling, is usually a single constant for a given system. Here, we have developed a unique architecture in which excitons in an aligned single-chirality carbon nanotube film interact with cavity photons in polarization-dependent manners. The system reveals ultrastrong coupling (VRS up to 329 meV or a coupling-strength-to-transition-energy ratio of 13.3%) for polarization parallel to the nanotube axis, whereas VRS is absent for perpendicular polarization. Between these two extremes, VRS is continuously tunable through polarization rotation with exceptional points separating crossing and anticrossing. The points between exceptional points form equienergy arcs onto which the upper and lower polaritons coalesce. The demonstrated on-demand ultrastrong coupling provides ways to explore topological properties of polaritons and quantum technology applications.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Kimble, H. J. in Cavity Quantum Electrodynamics (ed. Berman, P. R.) 203–266 (Academic Press, Boston, 1994).
Vasanelli, A., Todorov, Y. & Sirtori, C. Ultra-strong light–matter coupling and superradiance using dense electron gases. C. R. Phys. 17, 861–873 (2016).
Günter, G. et al. Sub-cycle switch-on of ultrastrong light–matter interaction. Nature 458, 178–181 (2009).
Törmä, P. & Barnes, W. L. Strong coupling between surface plasmon polaritons and emitters: a review. Rep. Prog. Phys. 78, 013901 (2015).
Zhang, X., Zou, C.-L., Jiang, L. & Tang, H. X. Strongly coupled magnons and cavity microwave photons. Phys. Rev. Lett. 113, 156401 (2014).
Yoshihara, F. et al. Superconducting qubit-oscillator circuit beyond the ultrastrong-coupling regime. Nat. Phys. 13, 44–47 (2017).
Casanova, J., Romero, G., Lizuain, I., Garc¡a-Ripoll, J. J. & Solano, E. Deep strong coupling regime of the Jaynes-Cummings model. Phys. Rev. Lett. 105, 263603 (2010).
Ciuti, C., Bastard, G. & Carusotto, I. Quantum vacuum properties of the intersubband cavity polariton field. Phys. Rev. B 72, 115303 (2005).
Ciuti, C. & Carusotto, I. Input-output theory of cavities in the ultrastrong coupling regime: the case of time-independent cavity parameters. Phys. Rev. A 74, 033811 (2006).
Moore, G. T. Quantum theory of the electromagnetic field in a variable-length one-dimensional cavity. J. Math. Phys. 11, 2679–2691 (1970).
Fulling, S. A. & Davies, P. C. W. Radiation from a moving mirror in two dimensional space-time: Conformal anomaly. Proc. R. Soc. London Ser. A 348, 393–414 (1976).
Kardar, M. & Golestanian, R. The “friction” of vacuum, and other fluctuation-induced forces. Rev. Mod. Phys. 71, 1233–1245 (1999).
Stassi, R., Ridolfo, A., Di Stefano, O., Hartmann, M. J. & Savasta, S. Spontaneous conversion from virtual to real photons in the ultrastrong-coupling regime. Phys. Rev. Lett. 110, 243601 (2013).
Ridolfo, A., Leib, M., Savasta, S. & Hartmann, M. J. Photon blockade in the ultrastrong coupling regime. Phys. Rev. Lett. 109, 193602 (2012).
De Liberato, S. Light–matter decoupling in the deep strong coupling regime: the breakdown of the Purcell effect. Phys. Rev. Lett. 112, 016401 (2014).
Hepp, K. & Lieb, E. H. On the superradiant phase transition for molecules in a quantized radiation field: the Dicke maser model. Ann. Phys. 76, 360–404 (1973).
Wang, Y. K. & Hioe, F. T. Phase transition in the Dicke model of superradiance. Phys. Rev. A 7, 831–836 (1973).
Weisbuch, C., Nishioka, M., Ishikawa, A. & Arakawa, Y. Observation of the coupled exciton–photon mode splitting in a semiconductor quantum microcavity. Phys. Rev. Lett. 69, 3314–3317 (1992).
Lidzey, D. G. et al. Strong exciton–photon coupling in an organic semiconductor microcavity. Nature 395, 53–55 (1998).
Gambino, S. et al. Exploring light–matter interaction phenomena under ultrastrong coupling regime. ACS Photon. 1, 1042–1048 (2014).
Liu, X. et al. Strong light–matter coupling in two-dimensional atomic crystals. Nat. Photon. 9, 30–34 (2015).
Graf, A., Tropf, L., Zakharko, Y., Zaumseil, J. & Gather, M. C. Near-infrared exciton–polaritons in strongly coupled single-walled carbon nanotube microcavities. Nat. Commun. 7, 13078 (2016).
Graf, A. et al. Electrical pumping and tuning of exciton–polaritons in carbon nanotube microcavities. Nat. Mater. 16, 911–917 (2017).
Heiss, W. The physics of exceptional points. J. Phys. A 45, 444016 (2012).
Dembowski, C. et al. Experimental observation of the topological structure of exceptional points. Phys. Rev. Lett. 86, 787–790 (2001).
Choi, Y. et al. Quasieigenstate coalescence in an atom-cavity quantum composite. Phys. Rev. Lett. 104, 153601 (2010).
Zhen, B. et al. Spawning rings of exceptional points out of Dirac cones. Nature 525, 354–358 (2015).
Gao, T. et al. Observation of non-Hermitian degeneracies in a chaotic exciton–polariton billiard. Nature 526, 554–558 (2015).
Peng, B. et al. Chiral modes and directional lasing at exceptional points. Proc. Natl Acad. Sci. USA 113, 6845–6850 (2016).
Peng, B. et al. Loss-induced suppression and revival of lasing. Science 346, 328–332 (2014).
He, X. et al. Wafer-scale monodomain films of spontaneously aligned single-walled carbon nanotubes. Nat. Nanotech. 11, 633–638 (2016).
Komatsu, N. et al. Modulation-doped multiple quantum wells of aligned single-wall carbon nanotubes. Adv. Func. Mater. 27, 1606022 (2017).
Fagan, J. A. et al. Isolation of specific small-diameter single-wall carbon nanotube species via aqueous two-phase extraction. Adv. Mat. 26, 2800–2804 (2014).
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110 (1954).
Zhang, Q. et al. Collective non-perturbative coupling of 2D electrons with high-quality-factor terahertz cavity photons. Nat. Phys. 12, 1005–1011 (2016).
Kéna-Cohen, S., Maier, S. A. & Bradley, D. D. C. Ultrastrongly coupled exciton–polaritons in metal-clad organic semiconductor microcavities. Adv. Opt. Mater. 1, 827–833 (2013).
Brodbeck, S. et al. Experimental verification of the very strong coupling regime in a GaAs quantum well microcavity. Phys. Rev. Lett. 119, 027401 (2017).
Yuen-Zhou, J. et al. Plexciton Dirac points and topological modes. Nat. Commun. 7, 11783 (2016).
Yuen-Zhou, J., Saikin, S. K., Yao, N. Y. & Aspuru-Guzik, A. Topologically protected excitons in porphyrin thin films. Nat. Mater. 13, 1026–1032 (2014).
Riek, C. et al. Direct sampling of electric-field vacuum fluctuations. Science 350, 420–423 (2015).
Benea-Chelmus, I.-C. Subcycle measurement of intensity correlations in the terahertz frequency range. Phys. Rev. A 93, 043812 (2016).
Riek, C. et al. Subcycle quantum electrodynamics. Nature 541, 376–379 (2017).
Acknowledgements
We thank D. Hagenmüller and J. Yuen-Zhou for useful discussion. This work was supported by the Department of Energy Basic Energy Sciences through grant no. DE-FG02-06ER46308 (optical spectroscopy experiments), the National Science Foundation through award no. ECCS-1708315 (device fabrication) and the Robert A. Welch Foundation through grant no. C-1509 (sample preparation). M.B. was supported by JST PRESTO (grant no. JPMJPR1767), KAKENHI (grant no. 26287087) and ImPACT Program of Council for Science, Technology and Innovation (Cabinet Office, Government of Japan).
Author information
Authors and Affiliations
Contributions
W.G. prepared the aligned SWCNT films, fabricated the devices and performed all measurements under the guidance of J.K. X.L. performed the transfer-matrix method simulations. M.B. developed the comprehensive theoretical model to explain the angular dependence of the coupling strength. All authors discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures.
Supplementary Video 1
Dispersion surface video.
Rights and permissions
About this article
Cite this article
Gao, W., Li, X., Bamba, M. et al. Continuous transition between weak and ultrastrong coupling through exceptional points in carbon nanotube microcavity exciton–polaritons. Nature Photon 12, 362–367 (2018). https://doi.org/10.1038/s41566-018-0157-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-018-0157-9
This article is cited by
-
Energy cascades in donor-acceptor exciton-polaritons observed by ultrafast two-dimensional white-light spectroscopy
Nature Communications (2022)
-
Polariton condensates for classical and quantum computing
Nature Reviews Physics (2022)
-
A non-Hermitian optical atomic mirror
Nature Communications (2022)
-
Microcavity-like exciton-polaritons can be the primary photoexcitation in bare organic semiconductors
Nature Communications (2021)
-
Maximal Shannon entropy in the vicinity of an exceptional point in an open microcavity
Scientific Reports (2020)