Abstract
Solid-state spin–photon interfaces that combine single-photon generation and long-lived spin coherence with scalable device integration—ideally under ambient conditions—hold great promise for the implementation of quantum networks and sensors. Despite rapid progress reported across several candidate systems, those possessing quantum coherent single spins at room temperature remain extremely rare. Here we report quantum coherent control under ambient conditions of a single-photon-emitting defect spin in a layered van der Waals material, namely, hexagonal boron nitride. We identify that the carbon-related defect has a spin-triplet electronic ground-state manifold. We demonstrate that the spin coherence is predominantly governed by coupling to only a few proximal nuclei and is prolonged by decoupling protocols. Our results serve to introduce a new platform to realize a room-temperature spin qubit coupled to a multiqubit quantum register or quantum sensor with nanoscale sample proximity.
Similar content being viewed by others
Main
Scalable spin–photon quantum interfaces require single-photon generation with a level structure that enables optical access to the electronic spins1,2,3. These systems are critical for the deployment of applications such as quantum repeaters4,5,6 and quantum sensors7,8,9,10. Ideally, a spin–photon interface should display long-lived spin coherence with efficient and coherent optical transitions in a scalable material platform without requiring stringent operation conditions such as cryogenic temperature or applied magnetic field. Materials that host atomic defects with well-defined optical and spin transitions garner the most attention. Several systems have been studied in detail11,12,13,14,15, but only a few individually addressable defects in diamond and silicon carbide possess quantum coherent spins at room temperature, although with challenging optical properties2,16,17. Realizing the ideal spin–photon interface requires engineering existing candidates for better performance, as well as exploring new material systems3,18.
Layered materials have emerged as a new quantum platform where their natural suitability for large-area growth, deterministic defect creation and hybrid device integration may enable accelerated scalability19,20,21,22,23. Hexagonal boron nitride (hBN) is a wide-bandgap (~6 eV) layered material that hosts a plethora of lattice defects that emit across the visible and near-infrared spectral regions. The first spin signature for hBN defects came from ensembles attributed to a boron vacancy (VB−) with a broad optical emission spectrum centred at ~800 nm (refs. 24,25). These defects have been subject to spin initialization and manipulation, although exclusively on an ensemble level due to their low optical quantum efficiency26,27,28,29. In contrast, defects in the visible spectrum (~600 nm) generate bright, tuneable, single-photon emission of up to 80% into the zero-phonon line at room temperature30,31,32,33,34. Preliminary reports on these optically isolated defects captured spin signatures via optically detected magnetic resonance (ODMR), but these signatures are only present under a finite magnetic field, indicating either a spin-triplet (S = 1) with low zero-field splitting or a spin-half (S = 1/2) system35,36,37.
In this work, we implement room-temperature coherent spin control of individually addressable single-photon-emitting defects in hBN. We reveal a spin-triplet (S = 1) ground-state spin manifold with 1.96 GHz zero-field splitting using angle-resolved magneto-optical measurements. We observe that the principal symmetry axis of the defect lies in the plane of the hBN layers, indicating a low-symmetry chemical structure. Microwave-based Ramsey interferometry reveals an inhomogeneous dephasing time \({T}_{2}^{\,* }\) of ~100 ns. Interestingly, the continuously driven spin Rabi coherence time (TRabi) is prolonged beyond 1 μs at room temperature with no magnetic field. This drive-prolonged coherence time indicates that the electronic spin can be protected from its reversibly decohering environment, the nuclei. We confirm this via standard dynamical decoupling pulse protocols yielding a spin-echo coherence time (TSE) of ~200 ns, which exceeds ~1 μs with ten refocusing pulses. The scaling of the coherence time with the number of decoupling pulses, together with the fine structure of the ODMR signal, suggests hyperfine coupling to only a few inequivalent nitrogen and boron nuclei.
A ground-state electronic spin triplet
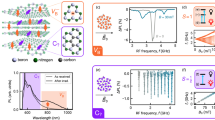
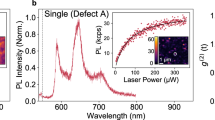
We investigate multilayer hBN that is grown via metal–organic vapour phase epitaxy using a carbon precursor and ammonia38, resulting in single-photon-emitting and spin-active defects that are related to carbon38,39. The flow rate of the carbon precursor determines the defect density in hBN and a 10 μmol min−1 flow rate yields an individually addressable defect density of ~1 defect per μm2. Figure 1a (top-right inset) shows a confocal scan image of the photoluminescence (PL) of the hBN material under 532 nm laser illumination (Supplementary Figs. 1 and 2 and Supplementary Section 1.3). The same material was the subject of a previous investigation that identified emitters displaying single-spin resonance under a magnetic field, assigned to an S > 1/2 system with low zero-field splitting36. To identify the ground-state spin resonances, we measure continuous-wave ODMR, using the protocol presented in Fig. 1a (bottom-right inset). Figure 1a shows an example ODMR spectrum for a single defect in the absence of the applied magnetic field and at room temperature. The ODMR signal displays strikingly strong contrast reaching nearly 50%. Unlike all the previous reports on single-spin-active hBN defects, the spectrum shows two distinct resonances, namely, υ1 = 1.87 GHz and υ2 = 1.99 GHz, in the absence of a magnetic field. We note that some defects also show the previously reported36 ODMR resonance with low zero-field splitting when a magnetic field is applied (Supplementary Figs. 8–10). We confirm that the presence of both resonances cannot be explained by a single-spin model (Supplementary Section 4), indicating the possibility that these two resonances relate to different charge or electronic states of the same defect.
a, An ODMR spectrum of a single defect in hBN measured in the absence of a magnetic field. The top-right inset shows a confocal image of the PL intensity of the hBN device under 532 nm laser illumination. Scale bar, 0–300 kcps. The bottom-right inset shows the measurement sequence. b, ODMR resonance frequencies for a defect, where the magnetic field is applied in the plane of the hBN layers along the defect z axis (θ0 = 0°) (purple circles) and 60° from the z axis (θ0 = 60°) (pink circles). Both measurements are fit with an S = 1 model using equation (1) (purple and pink curves, respectively). The inset defines the orientation of the magnetic field relative to the defect z axis and the hBN layers, identified by θ0. c, Inferred level structure for the defect, displaying a spin-triplet ground state and a spin-singlet metastable state. The green arrows show optical excitation; yellow arrows, PL; black arrows, intersystem crossing; and pink arrows, microwave (MW) drive. d,e, Statistical distribution of the D and E zero-field splitting parameters obtained from 25 defects. f, Spin–lattice relaxation time (T1) measurement of the ground-state spin, measured in the absence of a magnetic field. The inset shows the microwave measurement sequence (not drawn to scale), where r is the reference readout, s is the signal readout and t is the pulse delay. g, Second-order intensity-correlation measurement (g(2)(t)) of a single defect.
The observation of a zero-field resonance unambiguously determines a spin multiplicity of >½, indicating that this spin resonance is distinct from previous reports35,37. We assign the two resonances to the expected transitions of a spin triplet with lifted three-fold degeneracy between the spin sublevels, ruling out higher spin configurations (Supplementary Section 4). An effective-spin Hamiltonian describes the eigenstates of the S = 1 system, which, in the absence of hyperfine coupling, takes the following form:
where S is the spin vector with projection operators Sx, Sy and Sz; ge is the free electron g-factor, μB is the Bohr magneton and B is the magnetic field with magnitude B0. The zero-field transitions are characterized by the parameters D and E, where υ1,2 = (D ± E)/h and h is Planck’s constant. The ODMR spectrum (Fig. 1a) yields D/h = 1.930(10) GHz and E/h = 60(10) MHz. To confirm the S = 1 assignment, we perform vector-magnetic-field-dependent ODMR measurements. Figure 1b displays an example of the dependence of the ODMR transition frequencies as the external magnetic field is applied at θ0 = 0° (dark purple circles) and θ0 = 60° (light pink circles), where θ0 is the angle between B and the defect z axis. We determined that the defect z axis lies in the plane of the hBN layers (Fig. 1b, inset), for all the defects that we study, with a confidence of ~18°, via a series of angular ODMR measurements (Supplementary Figs. 11–14). The purple and pink curves show the simulated transition frequencies between the eigenstates of the S = 1 spin Hamiltonian of equation (1), with D/h = 1.959 GHz and E/h = 59 MHz. The same model effectively captures the appearance of the anticipated |+〉 to |−〉 (where |±〉 = 2−1/2|(+1 ± −1)〉) transition in the high off-axis-field regime. Interestingly, the ODMR contrast is not quenched up to >100 mT magnetic field applied orthogonal to the defect z axis—the highest magnetic-field strengths we access (Supplementary Fig. 16). Figure 1c illustrates the assigned energy-level structure, complete with a ground-state S = 1 system with 1.96 GHz zero-field splitting and a metastable spin-singlet state responsible for off-resonance optical spin initialization16. We measure the ground-state resonance across more than 25 defects across multiple devices and obtain a narrow distribution of D and E values: D/h = 1.971(25) GHz and E/h = 62(10) MHz (Fig. 1d,e). Due to sufficiently large zero-field splitting parameters, each electronic spin resonance can be independently addressed. Therefore, Fig. 1f presents an example measurement of the spin–lattice relaxation (T1) time, where the inset shows the protocol used for pulsed ODMR, including a calibrated sequence of laser, microwave and readout pulses for spin initialization, spin control and spin readout, respectively (Supplementary Figs. 18 and 19). The measured T1 values vary in the range of 35–200 μs, which is long compared with the optically excited-state lifetime of ~5 ns (Supplementary Fig. 4) and that of the previously identified resonance (~9 μs (Supplementary Fig. 20)). We conclude that this resonance arises from a ground-state S = 1 system. Figure 1g shows an example second-order intensity-correlation measurement, g(2)(t), of this defect (Supplementary Figs. 3 and 4 show additional defects).
Spin coherence and protection under ambient conditions
Figure 2a shows example spin Rabi oscillations, where we vary the duration of a resonant microwave pulse and measure the ODMR contrast. The data (purple circles) are fit to a function of the form exp(−τ/TRabi)sin(2πτΩ − φ) (red curve), where φ is the phase offset, Ω is the Rabi drive frequency and TRabi is the lifetime of Rabi oscillations. We confirm that Ω shows a linear dependence on the square root of the microwave power (Supplementary Fig. 21), as expected. Surprisingly, the oscillations persist for over a microsecond (TRabi = 1.20(6) μs), yielding a π-pulse fidelity of 0.96(2) and a quality factor (Q = TRabi/Tπ) of 24(3). However, as highlighted by the example shown in Fig. 2b, TRabi also displays a notable prolongation as a function of Ω—a signature behaviour for a spin-rich environment, observed in other III–V materials40,41. In this regime, the strongly driven spin is effectively decoupled from a slowly evolving nuclear environment akin to motional narrowing42.
a, Rabi oscillations (purple circles) for a single hBN defect measured at high microwave power, fit to a function of the form exp(−t/TRabi)sin(2πtΩ − φ) (orange curve), where φ is the phase offset, Ω is the Rabi frequency and TRabi is the decay lifetime of the Rabi oscillations. The inset shows a zoomed-in view of the data. b, Q factor of the Rabi oscillations as a function of the Rabi frequency, where Q = TRabi/Tπ and Tπ = 1/2Ω. The presented data (purple circles) are calculated using TRabi and Tπ extracted from fits to Rabi measurements using the equation above. The error bars are obtained from the 68% confidence intervals of each fit parameter. The Rabi measurement sequence is drawn above the panel (not drawn to scale), where r is the reference readout, s is the signal readout and t is the pulse duration. c, Ramsey measurements for different values of microwave frequency detuning Δ, from the resonance. The red curves are fit to exp(–\({t}{/}{{T}}_{{2}}^{{\,* }}{}\))sin(2πτΩRamsey − φ). The diagram above the panel shows the microwave measurement sequence (not drawn to scale), where r is the reference readout, s is the signal readout and t is the pulse delay. All the measurements are measured in the absence of a magnetic field.
To obtain the bare inhomogeneous dephasing time (\({{T}}_{{2}}^{{\,* }}\)) for the single defect, we perform microwave-based Ramsey interferometry. Figure 2c presents the Ramsey measurements for five values of detuning Δ between the microwave drive frequency and υ1 transition. Here the red curves are fit to the data using exp(–\({t }{/}{{T}}_{{2}}^{{\,* }}{}\))sin(2πτΩRamsey − φ), where ΩRamsey is the frequency of oscillations arising from Δ. We extract a collective value for \({{T}}_{{2}}^{{\,* }}\) of 106(12) ns, commensurate with the ~10 MHz linewidth of the unsaturated ODMR spectrum.
Figure 3a presents spin coherence measurements using a basic multipulse dynamical decoupling protocol, without phase control or pulse corrections (measurement sequence illustrated in the inset). Here spin-echo measurements (red circles), comprising a single refocusing pulse, Nπ = 1, yields TSE = 228(11) ns and α = 1.81(22) by fitting to exp[−(τ/TSE)α] (red curve). This value is comparable with TSE ≈ 100 ns determined for VB−-defect ensembles in hBN under equivalent conditions26,29. We further prolong the spin coherence time by including additional refocusing pulses. Figure 3a displays a range of measurements (Nπ = 2, 4, 6, 10) plotted in orange-to-blue colour-coded data (circles) and the corresponding fits (curves). The drop in ODMR contrast with increasing Nπ is due to the limited π-pulse fidelity in the multipulse experiment. Figure 3b presents the dependence of the protected spin coherence time TDD as a function of Nπ, reaching 1.08(4) µs with ten refocusing pulses. The inset shows the evolution of α values extracted from Fig. 3a fits as a function of Nπ, staying above 2 for all the values and reaching ~5 for 10 pulses, indicating strong protection. The orange curve (Fig. 3b) is a power-law fit yielding a TDD scaling of \({{N}}_{{\uppi }}^{{0}{.}{71}{(}{4}{)}}\). This scaling exponent falls close to the 0.67 scaling signature expected theoretically for a central electronic spin interacting weakly with a few slowly evolving proximal nuclei43,44.
a, Dynamic decoupling measurements with Nπ refocusing pulses, where each measurement is fit to exp[−(t/TDD)α]. The measurement sequence is shown in the inset, where r is the reference readout, s is the signal readout and t is the pulse delay. b, Spin coherence time TDD (purple triangles) as a function of the number of refocusing pulses Nπ. The orange curve is fit to a power law, \(\sim {{N}_{\uppi }}^{\gamma }\). The data (purple triangles) are extracted from fits to the data shown here. The error bars indicate the 68% confidence interval. All the measurements are performed in the absence of applied magnetic field.
Hyperfine signatures of proximal nuclei
To understand the nature of hyperfine coupling and gain an insight into the chemical structure of the defect, we investigate the υ1 resonance for the presence of spectral fine structure. Figure 4a presents a map of Rabi oscillations as a function of microwave detuning, performed in the absence of applied magnetic field and below saturation, where a multipeak structure is evident. An integrated linecut of this map between 0 and 100 ns reveals two maxima separated by approximately 10 MHz (Fig. 4b). This value is commensurate with the unsaturated ODMR linewidth and the 1/\({T}_{2}^{\,* }\) value. Figure 4c,d presents the unsaturated ODMR spectra and Rabi oscillations, respectively, performed with the magnetic field oriented ~60° with respect to the defect z axis. The unsaturated zero-field ODMR spectrum is narrow and asymmetric with a linewidth of the order of 10 MHz (Fig. 4 and Supplementary Fig. 22). With increasing magnetic field, the ODMR spectrum broadens, and we observe faster dephasing of Rabi oscillations. The purple circles in Fig. 4e show the ODMR spectrum for 3-mT magnetic field orthogonal to the z axis (θ0 = 90°). In this configuration, in contrast to T field applied at 60°, the ODMR spectrum remains narrow and asymmetric as that in the absence of a magnetic field. Figure 4f presents the ODMR spectrum for 20 mT magnetic field applied parallel to the z axis (θ0 = 0°). In this case, the ODMR lineshape is symmetric and structured, indicating a discrete number of overlapping hyperfine resonances (Supplementary Section 4). The orange-shaded curves under the ODMR spectra (Fig. 4e,f) are the ODMR spectra computed for an S = 1 electronic spin coupled to two inequivalent nuclear spins with hyperfine couplings of 13 and 22 MHz (Supplementary Information). These nuclear spins can be of different species (for example, one N and one B), or the same species with different hyperfine couplings (Supplementary Fig. 23). In fact, the computed spectrum (Fig. 4f) corresponds to hyperfine coupling to two 14N atoms. Strikingly, an S = 1 central spin coupled to two inequivalent nuclei is the only model that captures the magnetic-field amplitude and orientation dependence of the ODMR spectrum (Supplementary Fig. 24). These results, together with the in-plane symmetry of the defect, provide valuable insights for theoretical efforts aimed at determining the microscopic structure of this carbon-based spin-triplet defect45,46,47.
a, Rabi oscillations as a function of microwave frequency, measured at low microwave power. b, Linecut of the data in a, integrated over the first 100 ns. The presented data are the mean ± one standard deviation; N = 10. c,d, ODMR spectra and Rabi oscillations measured between 0 and 5 mT oriented at an arbitrary angle to the defect z axis. e, ODMR spectrum measured for 3 mT magnetic field orthogonal to the defect z axis. f, ODMR spectrum measured with 20-mT magnetic field parallel to the defect z axis. The shaded curves in e and f are the computed spectra (Supplementary Section 4).
In the low-field regime, the fine structure of the ODMR spectrum is intricately linked to the low-symmetry character of the defect. For an S = 1 electronic spin, the non-zero transverse zero-field splitting E gives rise to an avoided crossing at zero magnetic field, which may be accompanied by the quenching of a relatively weaker hyperfine interaction. However, if the strength of the hyperfine coupling to neighbouring nuclei is comparable with E/h, then it introduces an asymmetric perturbation to the ODMR spectrum, as observed here. The presence of the avoided crossing effectively results in a clock transition with the corresponding protection of the electronic spin coherence at zero magnetic field. In the low-field regime, when the magnetic field is applied orthogonal to the defect z axis, the clock-transition character of the υ1 line is preserved, whereas a magnetic field applied parallel to the defect z axis brings the system away from the clock-transition point. Therefore, the ODMR spectrum shown in Fig. 4e is reminiscent of the zero-field spectrum of Fig. 4c, whereas the 3 mT spectrum shown in Fig. 4c is considerably broadened, compatible with our identification of a low-symmetry spin-triplet defect. We believe that the confirmation of a low-symmetry structure rules out single-site vacancies, single-atom substituents and carbon tetramers47 as potential chemical structures for this defect (Supplementary Section 4.3). Carbon trimers45,48 and vacancy-substituent complexes49 are low symmetry, but structures that have been theoretically considered to date are not predicted to display S = 1 with ~2 GHz zero-field splitting48,49. Larger carbon defects (namely, C4(cis and trans)) or complexes involving carbon or oxygen50 are potential candidates51, but these structures need to be investigated further.
Identification of a D = 1.96 GHz, S = 1 ground-state spin resonance for defects that simultaneously show a lower-frequency spin resonance, characterized previously on the same material36, indicates that these resonances are related. We conjecture that we identify the true ground state for a class of visible-emitting hBN defects, where previous reports of single-defect ODMR may have focused on the excited state, charge state or an alternative defect type. This is supported by our repeat identification of single defects that show both resonances with comparable contrast values and frequencies that cannot be explained by a single-spin model (Supplementary Sections 2.2 and 4). Alternatively, the identification of two spin resonances on a single defect could point towards complex charge state dynamics, which remains to be explored.
Outlook
An optically addressable S = 1 defect with proximal nuclei displaying quantum coherence at room temperature and zero magnetic field in a layered material offers immense promise for quantum technologies. For quantum networks, this system can offer a feasible scaling of quantum repeater hardware under ambient operation conditions provided the necessary optical quality is delivered via integrated quantum photonics systems. The layered material nature of hBN may facilitate integration into nanostructures for tuning the spin and optical properties via the application of strain and electric fields without compromising quality. The proximal nuclear spins, coupled to the electronic spin, present an opportunity for the realization of long-lived quantum registers for the electronic spin qubit—a critical element for large-scale quantum architectures. For quantum sensing, this defect offers a unique and flexible system capable of nanoscale sensing under ambient conditions. The defects reported here are at most 15 nm away from any surface, highlighting their potential as highly proximal nanoscale sensors. We estimate a minimum detectable d.c. magnetic field of 3 μT Hz–1/2, using 0.77(h/geμB)\({(}{\Delta }{\nu }{/}{C}\sqrt{{R}}{)}\) (ref. 52), where Δν is the linewidth (10 MHz), C is the contrast (30%) and R is the measure of brightness (105 events per second). This estimate is of the same order as that of the well-established nitrogen-vacancy centres in diamond, with the added advantage of a system that is somewhat resilient to surface charge noise. Further, the retention of high ODMR contrast under an off-axis magnetic field offers flexibility on the dynamic range of vector magnetometry measurements.
Methods
Materials preparation
Multilayer hBN was grown by metal–organic vapour phase epitaxy on sapphire36,38,39. Briefly, triethyl boron and ammonia were used as boron and nitrogen sources, respectively, with hydrogen used as the carrier gas. Growth was performed at low pressure (85 mbar) and at a temperature of 1,350 °C, on sapphire substrates. Isolated defects were generated by modifying the flow rate of triethyl boron during growth, a parameter known to control the incorporation of carbon within the resulting hBN sheets39. The resulting material is ~30 nm thick. For confocal PL measurements, the hBN sheets were transferred to SiO2/Si substrates, using a water-assisted self-delamination process to avoid polymer contamination.
Experimental setup
We perform optical measurements at room temperature under ambient conditions using a home-built confocal microscopy setup36. We use a continuous-wave 532 nm laser (Ventus 532, Laser Quantum) that is passed through a 532 nm band-pass filter, onto a scanning mirror and focused on the device using an objective lens with ×100 magnification and a numerical aperture of 0.9. We control the excitation power using an acousto-optic modulator (AA Optoelectronics), with the first-order diffracted beam fibre-coupled into the confocal setup. We remove any residual laser light from the collected emission using two 550 nm long-pass filters (Thorlabs FEL550). The remaining light was sent either into an avalanche photodiode (SPCM-AQRH-14-FC, Excelitas Technologies) for recording photon count traces or to a charge-coupled-device-coupled spectrometer (Acton Spectrograph, Princeton Instruments) via single-mode optical fibres (SM450 and SM600) for PL spectroscopy measurements. We carry out intensity-correlation measurements using a Hanbury Brown and Twiss interferometry setup using a 50:50 fibre beamsplitter (Thorlabs) and a time-to-digital converter (quTAU, qutools) with 81 ps resolution. We used a continuous-wave 405 nm laser (Thorlabs LP405-SF10) via a 405 nm dichroic mirror (Semrock BLP01-405R) to illuminate the sample for charge control.
ODMR
We perform ODMR measurements using the confocal setup described above. A copper coil was placed in front of the hBN sample, with optical access through the coil, to provide an out-of-plane oscillating magnetic field. For continuous-wave ODMR measurements, a 70 Hz square-wave modulation was applied to the microwave amplitude to detect the change in PL counts as a function of microwave frequency. For pulsed ODMR, a calibrated pulse sequence or laser, microwave and readout pulses are used to determine the defect count rate with or without the presence of a spin-flipping microwave pulse. As for continuous-wave ODMR, the ODMR contrast (C) is given by C = Isig – Iref/Iref, where Isig and Iref are the number of counts detected in the signal or reference, respectively. For measurements in the absence of an applied magnetic field, these were not measured in a shielded environment and therefore were susceptible to the Earth’s magnetic field and magnetic components on the optical table (~0.4 mT). For measurements under an applied magnetic field, we use a permanent magnet on a translation stage that can be changed in proximity and orientation relative to the device. We perform pulsed ODMR measurements using a pulse streamer (Swabian 8/2) to control a series of switches (Mini-Circuits ZYSWA-2-50DR+) to modulate the laser power, microwave power and signal readout duration.
Data availability
All data needed to evaluate the conclusions in the paper are present in the Article or its Supplementary Information. All datasets are available from the corresponding authors upon reasonable request.
Code availability
All codes used to generate the figures and analyse the data are available from the corresponding authors upon reasonable request.
References
Awschalom, D. D., Hanson, R., Wrachtrup, J. & Zhou, B. B. Quantum technologies with optically interfaced solid-state spins. Nat. Photon. 12, 516–527 (2018).
Atatüre, M., Englund, D., Vamivakas, N., Lee, S.-Y. & Wrachtrup, J. Material platforms for spin-based photonic quantum technologies. Nat. Rev. Mater. 3, 38–51 (2018).
Wolfowicz, G. et al. Quantum guidelines for solid-state spin defects. Nat. Rev. Mater. 6, 906–925 (2021).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Simon, C. Towards a global quantum network. Nat. Photon. 11, 678–680 (2017).
Pompili, M. et al. Realisation of a multimode quantum network of remote solid-state qubits. Science 372, 259–264 (2021).
Maze, J. et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 455, 644–647 (2008).
Taylor, J. et al. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 4, 810–816 (2008).
Aslam, N. et al. Nanoscale nuclear magnetic resonance with chemical resolution. Science 357, 67–71 (2017).
Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Robledo, L. et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574–578 (2011).
Doherty, M. W. et al. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).
Christle, D. J. et al. Isolated electron spins in silicon carbide with millisecond coherence times. Nat. Mater. 14, 160–163 (2015).
Pla, J. J. et al. High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 496, 334–338 (2013).
Higginbottom, D. B. et al. Optical observation of single spins in silicon. Nature 607, 266–270 (2022).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012).
Widmann, M. et al. Coherent control of single spins in silicon carbide at room temperature. Nat. Mater. 14, 164–168 (2015).
Bassett, L. C., Alkauskas, A., Exarhos, A. L. & Fu, K.-M. Quantum defects by design. Nanophotonics 8, 1867–1888 (2019).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Kim, S. M. et al. Synthesis of large-area multilayer hexagonal boron nitride for high material performance. Nat. Commun. 6, 8662 (2015).
Xia, F., Wang, H., Xiao, D., Dubey, M. & Ramasubramaniam, A. Two-dimensional material nanophotonics. Nat. Photon. 8, 899–907 (2014).
Gale, A. et al. Site-specific fabrication of blue quantum emitters in hexagonal boron nitride. ACS Photonics 9, 2170–2177 (2022).
Elshaari, A. W. et al. Deterministic integration of hBN emitter in silicon nitride photonic waveguide. Adv. Quantum Technol. 4, 2100032 (2021).
Gottscholl, A. et al. Initialization and read-out of intrinsic spin defects in a van der Waals crystal at room temperature. Nat. Mater. 19, 540–545 (2020).
Ivády, V. et al. Ab initio theory of the negatively charged boron vacancy qubit in hexagonal boron nitride. npj Comput. Mater. 6, 41 (2020).
Gottscholl, A. et al. Room temperature coherent control of spin defects in hexagonal boron nitride. Sci. Adv. 7, 14 (2021).
Baber, S. et al. Excited state spectroscopy of boron vacancy defects in hexagonal boron nitride using time-resolved optically detected magnetic resonance. Nano Lett. 22, 461–467 (2021).
Liu, W. et al. Coherent dynamics of multi-spin VB− center in hexagonal boron nitride. Nat. Commun. 13, 5713 (2022).
Ramsay, A. J. et al. Coherence protection of spin qubits in hexagonal boron nitride. Nat. Commun. 14, 461 (2023).
Tran, T. T., Bray, K., Ford, M. J., Toth, M. & Aharonovich, I. Quantum emission from hexagonal boron nitride monolayers. Nat. Nanotechnol. 11, 37–41 (2016).
Jungwirth, N. R. et al. Temperature dependence of wavelengths selectable zero-phonon emission from single defects in hexagonal-boron nitride. Nano Lett. 16, 6052–6057 (2016).
Grosso, G. et al. Tunable and high-purity room temperature single-photon emission from atomic defects in hexagonal boron nitride. Nat. Commun. 8, 705 (2017).
Noh, G. et al. Stark tuning of single-photon emitters in hexagonal boron nitride. Nano Lett. 18, 4710–4715 (2018).
Proscia, N. V. et al. Near-deterministic activation of room temperature quantum emitters in hexagonal boron nitride. Optica 5, 1128–1134 (2018).
Chejanovsky, N. et al. Single-spin resonance in a van der Waals embedded paramagnetic defect. Nat. Mater. 20, 1079–1084 (2021).
Stern, H. L. et al. Room-temperature optically detected magnetic resonance of single defects in hexagonal boron nitride. Nat. Commun. 13, 618 (2022).
Guo, N.-J. et al. Coherent control of an ultrabright single spin in hexagonal boron nitride at room temperature. Nat. Commun. 14, 2893 (2023).
Chugh, D. et al. Flow modulation epitaxy of hexagonal boron nitride. 2D Mater. 5, 045018 (2018).
Mendelson, N. et al. Identifying carbon as the source of visible single-photon emission from hexagonal boron nitride. Nat. Mater. 20, 321–328 (2021).
Bodey, J. H. et al. Optical spin locking of a solid-state qubit. npj Quantum Inf. 5, 95 (2019).
Koppens, F. H. L. et al. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 442, 766–771 (2006).
Bloembergen, N., Purcell, E. M. & Pound, R. V. Relaxation effects in nuclear magnetic resonance. Phys. Rev. 73, 679–715 (1948).
de Lange, G., Wang, Z. H., Ristè, D., Dobrovitski, V. V. & Hanson, R. Universal dynamic decoupling of a single solid-state spin from a spin bath. Science 330, 60–63 (2010).
Medford, J. et al. Scaling of dynamic decoupling for spin qubits. Phys. Rev. Lett. 108, 086802 (2012).
Jara, C. et al. First-principles identification of single-photon emitters based on carbon clusters in hexagonal boron nitride. J. Phys. Chem. A 125, 1325–1335 (2021).
Li, K., Smart, T. J. & Ping, Y. Carbon trimer as a 2 eV single-photon emitter candidate in hexagonal boron nitride: a first-principles study. Phys. Rev. Mater. 6, 4 (2022).
Benedek, Z. et al. Symmetric carbon tetramers forming spin qubits in hexagonal boron nitride. npj Comput. Mater. 9, 187 (2023).
Auberger, P. & Gali, A. Towards ab initio identification of paramagnetic substitutional carbon defects in hexagonal boron nitride acting as quantum bits. Phys. Rev. B 104, 075410 (2021).
Liu, W. et al. Spin-active defects in hexagonal boron nitride. Mater. Quantum. Technol. 2, 032002 (2022).
Li, S. & Gali, A. Identification of an oxygen defect in hexagonal boron nitride. J. Phys. Chem. Lett. 13, 9544–9551 (2022).
Maciaszek, M., Razinkovas, L. & Alkauskas, A. Thermodynamics of carbon point defects in hexagonal boron nitride. Phys. Rev. Mater. 6, 014005 (2022).
Dreau, A. et al. Avoiding power broadening in optically detected magnetic resonance of single NV defects for enhanced d.c. magnetic field sensitivity. Phys. Rev. B 84, 195204 (2011).
Acknowledgements
We thank Y. Ping, V. Ivády, J.-P. Tetienne, L. Zaporski and M. H. Appel for helpful discussions. We acknowledge support from the ERC Advanced Grant PEDESTAL (884745), the Australian Research Council (ARC) through grants CE200100010 and FT220100053, and the Office of Naval Research Global (N62909-22-1-2028). H.L.S. acknowledges a Royal Society fellowship. C.M.G. acknowledges support from the Netherlands Organisation for Scientific Research (NWO 019.221EN.004, Rubicon 2022-1 Science). Q.G. acknowledges financial support from the China Scholarship Council and the Cambridge Commonwealth, European & International Trust. S.E.B., O.F.J.P. and S.A.F. acknowledge funding from the Engineering and Physical Sciences Research Council (EPSRC) Centre for Doctoral Training (CDT) in Nanoscience and Nanotechnology (NanoDTC, grant no. EP/S022953/1). L.F. acknowledges the IDEX international internship scholarship from Paris-Saclay University.
Author information
Authors and Affiliations
Contributions
H.L.S., C.M.G., Q.G. and M.A. conceived the experiments. H.L.S., X.D. and S.E.B. performed the measurements with assistance from O.F.J.P., S.A.F. and L.F. C.L., H.H.T. and I.A. provided the samples. H.L.S. and C.M.G. performed the data analysis and wrote the manuscript. All authors contributed to the discussion of the results and the preparation of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Materials thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections 1–4 and Figs. 1–24.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stern, H.L., M. Gilardoni, C., Gu, Q. et al. A quantum coherent spin in hexagonal boron nitride at ambient conditions. Nat. Mater. 23, 1379–1385 (2024). https://doi.org/10.1038/s41563-024-01887-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-024-01887-z
This article is cited by
-
Low-symmetry vacancy-related spin qubit in hexagonal boron nitride
npj Computational Materials (2024)