Abstract
Quantum materials can display physical phenomena rooted in the geometry of electronic wavefunctions. The corresponding geometric tensor is characterized by an emergent field known as the Berry curvature (BC). Large BCs typically arise when electronic states with different spin, orbital or sublattice quantum numbers hybridize at finite crystal momentum. In all the materials known to date, the BC is triggered by the hybridization of a single type of quantum number. Here we report the discovery of the first material system having both spin- and orbital-sourced BC: LaAlO3/SrTiO3 interfaces grown along the [111] direction. We independently detect these two sources and probe the BC associated to the spin quantum number through the measurements of an anomalous planar Hall effect. The observation of a nonlinear Hall effect with time-reversal symmetry signals large orbital-mediated BC dipoles. The coexistence of different forms of BC enables the combination of spintronic and optoelectronic functionalities in a single material.
Similar content being viewed by others
Main
When moving along closed paths, electrons can accumulate a geometric Berry phase related to the flux of a field, called the Berry curvature (BC), encoding the geometric properties of the electronic wavefunctions. In magnetic materials, the adiabatic motion of electrons around the Fermi surface provides such a Berry phase. It is directly observable since it governs the intrinsic part of the anomalous Hall conductivity1,2. Anomalous Hall effect measurements, therefore, represent a charge transport footprint of the intrinsic geometric structure of electronic wavefunctions. In non-magnetic materials, the BC field is forced to vanish by symmetry when summed over the occupied electronic states. However, local concentrations of positive and negative BC in momentum space are allowed by acentric crystalline arrangements3. This segregation of BC in different regions of momentum space appears whenever electronic states with different internal quantum numbers are coupled to each other by terms that linearly depend on crystalline momentum k. In these regions, the electronic bands typically resemble the dispersion relations of relativistic Dirac or Weyl fermions. The spin–orbit linear-in-k coupling between different spin states shapes the Dirac cones at the surfaces of three-dimensional topological insulators4,5 as well as the Weyl cones of topological semimetals6. Couplings between different atomic orbital and sublattice states, instead, give rise to the (gapped) Dirac cones of transitional metal dichalcogenides and graphene. Conceptually speaking, the appearance of BC beyond this Dirac/Weyl paradigm is entirely allowed. The fundamental conditions for the occurrence of BC only involve the crystalline geometry of a material, with no restrictions on the specific properties of its low-energy electronic excitations. Achieving this challenge is of great interest. First, it could, in principle, result in the coexistence of different mechanisms of BC generation. This could be used, in turn, to endow a single-material system with different BC-mediated effects, for instance, spin and orbital Hall effects. Second, searching for BCs without Dirac or Weyl cones might allow the design of materials with interplay of correlated and topological physics—an unexplored frontier in condensed-matter physics.
Here we reach these two milestones in the two-dimensional electron system (2DES) confined at (111)-oriented oxide interfaces, with a high-temperature trigonal crystalline structure. This model system satisfies the crystalline symmetry properties for a non-vanishing BC. The combination of spin–orbit coupling, orbital degrees of freedom associated with the low-energy t2g electrons, and crystal fields leads to the coexistence of a spin-sourced and orbital-sourced BC. The two sources are independently probed using two different charge transport diagnostic tools. The observation of the BC-mediated anomalous planar Hall effect (APHE)7,8 grants direct access to the spin-sourced BC, whereas nonlinear Hall transport measurements in time-reversal symmetric conditions9,10 detect an orbital-mediated Berry curvature dipole (BCD)—a quantity measured so far only in gapped Dirac systems9,10,11,12,13,14,15,16,17,18,19 and three-dimensional topological semimetals20,21,22,23,24,25. We identify (111)-oriented LaAlO3/SrTiO3 heterointerfaces as an ideal material system because their 2DES features many-body correlations and a two-dimensional superconducting ground state26,27,28,29,30.
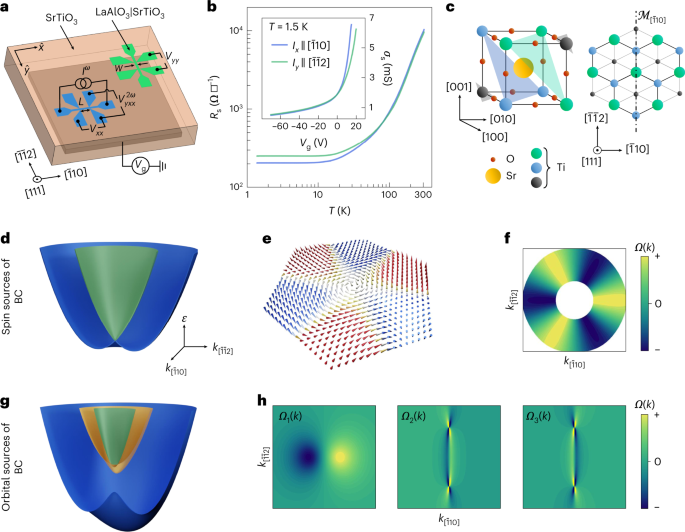
We synthesize (111)-oriented LaAlO3/SrTiO3 heterostructures by pulsed laser deposition (Methods). The samples are lithographically patterned into Hall bars oriented along the two orthogonal principal in-plane crystallographic directions: the \([\bar{1}10]\) and \([\bar{1}\bar{1}2]\) axis (Fig. 1a). The sheet conductance and carrier density of the 2DES are controlled by electrostatic-field effects in a back-gate geometry (Fig. 1b). We source an oscillating current (Iω) with frequency ω/2π along each Hall bar, and concomitantly measure the longitudinal response as well as the first- or second-harmonic transverse voltages in a conventional lock-in detection scheme (Fig. 1a).
a, Schematic of the electrical measurement configurations of two Hall bars, hosting a 2DES, and oriented along the \([\bar{1}10]\) and \([\bar{1}\bar{1}2]\) crystallographic axes. Here W is the width of the channel and L is the distance between the longitudinal voltage probes. Also, Vg stands for the high-voltage source used to tune the 2DES band occupation (Fermi energy) in a back-gate geometry. b, Sheet resistance Rs versus temperature T of the 2DES for the \([\bar{1}10]\) and \([\bar{1}\bar{1}2]\) Hall-bar devices, showing a nearly isotropic metallic character. The inset shows the sheet conductance, \({\sigma }_{{{{\rm{s}}}}}={R}_{{{{\rm{s}}}}}^{-1}\), as a function of back-gate voltage Vg, showing gate tunability of the 2DES at 1.5 K. c, Schematic of SrTiO3 perovskite cubic unit cell displaying the non-equivalent (111) titanium planes (shaded areas) (left). Top view along the [111] crystallographic direction, of the same unit cell, showing only the Ti atoms (right). The dash–dotted line indicates the mirror line \({{{{\mathcal{M}}}}}_{[\bar{1}10]}\). d, Schematic of a single pair of spin-split bands forming a Kramers’ pair at the Γ point up to the Fermi level. e, Each spin band is characterized by a non-trivial spin texture with out-of-plane spin components induced by the effect of trigonal warping. f, Exclusion plot of the BC Ωk over the Fermi surfaces of the two spin sub-bands. g, Schematic of the band structure of spin–orbit-free orbital bands corresponding to t2g electrons subject to a \({{{{\mathcal{C}}}}}_{\mathrm{s}}\) crystal field. At the centre of the BZ, all the levels are split. The orbital Rashba coupling (∝αm) leads to mirror-symmetry-protected crossings. h, Band-resolved BC displaying dipolar hotspots (left) in the lowest-energy band and singular pinch points in the highest-energy bands.
The non-trivial geometric properties of the electronic waves in the 2DES derive entirely from the triangular arrangement of the titanium atoms at the (111)-oriented LaAlO3/SrTiO3 interface (Fig. 1c). Together with the \({{{{\mathcal{M}}}}}_{\bar{1}10}\) mirror-line symmetry, this yields a \({{{{\mathcal{C}}}}}_{3v}\) crystallographic point group symmetry. As a result of this trigonal crystal field and the concomitant presence of spin–orbit coupling, the entire d-orbital manifold of Ti atoms located at the centre of the surface Brillouin zone (BZ) is split into five distinct Kramers’ pairs (Supplementary Note I). The energy bands of the pairs are shifted in momentum due to spin–orbit coupling. In their simplest form, they acquire a parabolic dispersion reminiscent of a Rashba 2DES (Fig. 1d). However, the trigonal crystal field brings about a specific hexagonal warping31,32 that has a twofold effect. First, for each time-reversal related pair of bands, the Fermi lines acquire a hexagonal ‘snowflake’ shape33. Second, and the most important, the spin texture in momentum space acquires a characteristic out-of-plane component34,35, with alternating meron and antimeron wedges respecting the symmetry properties of the crystal (Fig. 1e). This unique spin–momentum locking enables a non-vanishing local BC entirely generated by spin–orbit coupling (Supplementary Note I). The local BC of the spin-split bands of each pair cancel each other at the same crystal momentum. However, there is a region of crystal momenta populated by a single spin band. In this region (namely, the annulus between the two Fermi lines of the system), alternating positive and negative regions of non-vanishing BC are present (Fig. 1f).
Apart from the spin channel, an inherently different source of BC exists. In systems with orbital degrees of freedom, the lack of crystal centrosymmetry yields coupling that are linear in k, and mix different atomic orbital states. These orbital Rashba couplings36 are independent of the presence of spin–orbit coupling. Precisely as its spin counterpart, the orbital Rashba coupling can generate a finite BC37, but only when all the rotational symmetries are broken (Methods and Supplementary Note I). With a reduced \({{{{\mathcal{C}}}}}_{\mathrm{s}}\) symmetry, low-lying t2g orbitals are split into three non-degenerate levels. The corresponding orbital bands then realize a gapped Rashba-like spectrum with protected crossings along the mirror-symmetric lines of the two-dimensional BZ (Fig. 1g). These characteristics result in the appearance of dipolar BC hotspots and singular pinch points (Fig. 1h). Such orbital sources of BC are fully active at the (111) oxide interfaces owing to the reduced low-temperature symmetries. The cubic-to-tetragonal structural phase transition38,39 occurring at 110 K breaks the three-fold rotational symmetry along the [111] direction. In addition, the tetragonal to locally triclinic structural distortions at temperatures below ~70 K together with the ferroelectric instability40 below 50 K are expected to strongly enhance the orbital Rashba strength.
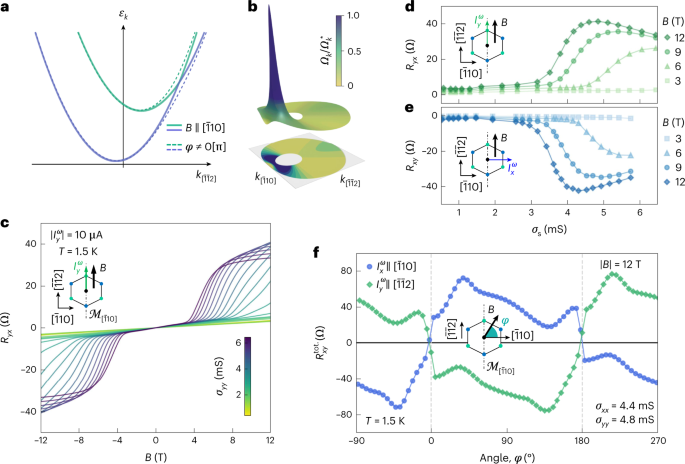
The orbital-sourced BC is expected to be very stiff in response to externally applied in-plane magnetic fields due to the absence of symmetry-protected orbital degeneracies. In contrast, the spin-sourced BC is substantially more susceptible to planar magnetic fields. As shown in Fig. 2a,b, an in-plane magnetic field is capable of generating a BC hotspot within the Fermi surface annulus. This BC hotspot corresponds to a field-induced avoided level crossing between the two spin-split bands that occurs whenever the applied magnetic field breaks the residual crystalline mirror symmetry. The momentum-integrated net BC is then non-zero (Supplementary Note II), and yields a transverse Hall conductance satisfying the antisymmetric property σxyρyx = −1, even in the absence of any Lorentz force. This effect, theoretically predicted elsewhere7,8 and known as the APHE, is different in nature with respect to the conventional planar Hall effect, which is instead related to the anisotropy in the longitudinal magnetoresistance and thus characterized by a symmetric response, namely, σxy(B) = σxy(–B).
a, Schematic of the energy dispersion of the spin-split bands along the mirror line of the BZ \({k}_{[\bar{1}10]}=0\) in the presence of a planar magnetic field. When the latter is oriented along the \([\bar{1}10]\) direction, there is a mirror-symmetry-protected crossing of the spin-split bands that evolves into an anticrossing for the other directions of the magnetic field. Angle φ is defined by the orientation of the magnetic field with respect to the \([\bar{1}10]\) crystallographic direction (schematic shown in the inset of f). b, Sketch of the spin-sourced BC-normalized magnitude \({{{\varOmega }}}_{k}/{{{\varOmega }}}_{k}^{\star }\) when the magnetic field is directed along the \([\bar{1}\bar{1}2]\) direction. When the anticrossing point enters the Fermi surface annulus, the integral of the BC is strongly enhanced and the APHE response reaches its maximum. c, Experimentally measured field-antisymmetric planar Hall resistance \({R}_{{{{{xy}}}}}={V}_{{{{{xy}}}}}^{\omega }/{I}_{{{{{x}}}}}^{\omega }\) at T = 1.5 K, with \({I}_{{{{{y}}}}}^{\omega }\) along \([\bar{1}\bar{1}2]\parallel B\) (schematic in the inset), for different sheet conductance values σyy indicated by the coloured scale bar. d, Corresponding dependence of Ryx versus σyy showing a non-monotonic behaviour for fixed values of B > 3 T, and an onset above a threshold value of σyy. e, Dependence of the field-antisymmetric contribution Rxy versus σxx for \({I}_{{{{{x}}}}}^{\omega }\) along \([\bar{1}10]\perp B\) (Extended Data Fig. 1). f, In-plane angular dependence of the raw total transverse-resistance response \({R}_{{{{{xy}}}}}^{{{{\rm{tot.}}}}}\), that is, not field-(anti)symmetrized, for the two Hall-bar devices at B = 12 T. The planar Hall response obeys the Onsager relation Rxy(B) = Ryx(–B), as evident from the near-identical angular dependence on imposing a ±π translation to either curve. Remarkably, \({R}_{{{{{xy}}}}}^{{{{\rm{tot.}}}}}\) goes to zero at φ = 0° and φ = 180°, that is, when the mirror symmetry is preserved even in the presence of an external magnetic field.
Figure 2c shows the transverse (Hall) resistance measured with a current applied along the \([\bar{1}\bar{1}2]\) crystal direction and with collinear current and magnetic field. This ensures a vanishing symmetric planar Hall effect7. At fields well below 4 T, a small signal increasing linearly with the field strength is detected. This feature can be attributed to an out-of-plane misalignment of the magnetic field smaller than 1.5° (Supplementary Note III). Above a magnetic-field threshold instead, a large transverse Hall signal sharply emerges (Extended Data Fig. 3). At even larger fields, this response saturates. Electrostatic gating is found to decrease the magnetic-field threshold and promotes a non-monotonic evolution of the response amplitude (Fig. 2d,e). The experimental features of this Hall response can be captured by considering a single pair of spin-split bands coupled to the external field by the Zeeman interaction. In this picture, the sudden onset of the transverse response is associated with the appearance of the BC hotspot inside the Fermi surface annulus occurring at a critical magnetic-field strength (Supplementary Note II). Magnetoconductance measurements in the weak antilocalization regime (Extended Data Fig. 4) show that the onset of the transverse Hall signal precisely coincides with the appearance of the spin-sourced BC hotspot (Extended Data Fig. 5). The non-monotonic behaviour of the transverse response as a function of electrostatic gating and magnetic-field strength can also be ascribed to the BC origin of the Hall response. The angular dependence of the transverse resistance (Fig. 2f) indicates a vanishing transverse linear conductivity when the planar magnetic field is along the \([\bar{1}10]\) direction, due to mirror symmetry \({{{{\mathcal{M}}}}}_{[\bar{1}10]}\). This is independent of whether the driving current is along the \([\bar{1}10]\) or \([\bar{1}\bar{1}2]\) direction. Note that the two angular dependencies are related to each other by a 180° shift, in agreement with the Onsager reciprocity relations41.
The absence of linear conductivity makes this configuration the ideal regime to investigate the presence of nonlinear transverse responses, which are symmetry-allowed when the driving current is collinear with the magnetic field (Supplementary Note II). We have, therefore, performed systematic measurements of the second-harmonic (2ω) transverse responses (Fig. 3a,b) by sourcing the a.c. current along the \([\bar{1}10]\) direction. We have subsequently disentangled the field-antisymmetric \({R}_{{{{{y}}}},{{{\rm{as}}}}}^{2\omega }=\left[{R}_{{{{{y}}}}}^{2\omega }(B)\,-\,{R}_{{{{{y}}}}}^{2\omega }(-B)\right]/2\) and field-symmetric \({R}_{{{{{y,\mathrm{sym}}}}}}^{2\omega }=\left[{R}_{{{{{y}}}}}^{2\omega }(B)\,+\,{R}_{{{{{y}}}}}^{2\omega }(-B)\right]/2\) contributions, since they originate from distinct physical effects. In particular, the antisymmetric part contains a semiclassical contribution that only depends on the conventional group velocity of the carriers at the Fermi level (Supplementary Note II). Conversely, the symmetric part originates from the anomalous velocity term of the carriers. It is a purely quantum contribution and can be expressed in terms of a BCD. We observe the following features in Fig. 3a,b. The semiclassical antisymmetric contribution has a sudden onset above a characteristic magnetic field (Fig. 3a) that is sensitive to gating (Fig. 3c). The gate dependence displays a monotonic growth consistent with its physical origin. On the contrary, the symmetric contribution displays the typical non-monotonous gate and field-amplitude dependence (Fig. 3b,d) of BC-mediated effects. The gate dependence of the nonlinear symmetric contribution obtained by sourcing the current along the \([\bar{1}\bar{1}2]\) direction is instead strongly suppressed and featureless (Fig. 3e). This is consistent with a \([\bar{1}10]\)-oriented BCD, which gives a vanishing response in this configuration. We note that the symmetric nonlinear transverse resistance has a characteristic quadratic current–voltage (Iω−V2ω), which—combined with the response at double the driving frequency—establishes its second-order nature (Fig. 3f).
a,b, Field-antisymmetric \({R}_{{{{{y}}}},{{{\rm{as}}}}}^{2\omega }\) (a) and field-symmetric \({R}_{{{{{y}}}},{{{\rm{sym}}}}}^{2\omega }\) (b) second-harmonic transverse-resistance responses for \({I}_{{{{{x}}}}}^{\omega }\) along \([\bar{1}10]\parallel B\), and for different values of sheet conductance σxx. c,d, Corresponding dependence of \({R}_{{{{{y}}}},{{{\rm{as}}}}}^{2\omega }\) (c) and \({R}_{{{{{y,\mathrm{sym}}}}}}^{2\omega }\) (d) versus σxx for different values of in-plane magnetic field B. The field-symmetric nonlinear transverse resistance displays a strong non-monotonic response, attributed to a Zeeman-induced Berry-phase contribution. e, Field-symmetric second-harmonic transverse-resistance response \({R}_{{{{{x}}}},{{{\rm{sym}}}}}^{2\omega }\) for \({I}_{{{{{y}}}}}^{\omega }\) along \([\bar{1}\bar{1}2]\perp B\) versus sheet conductance σyy at fixed values of the planar magnetic field (Extended Data Fig. 2). The full-scale ordinate axis is chosen to be the same as that in d for better comparison. f, Field-symmetric nonlinear second-harmonic transverse voltage \({V}_{{{{{yxx}}}},{{{\rm{sym}}}}}^{2\omega }\) versus the a.c. current amplitude \({I}_{{{{{x}}}}}^{\omega }\) at fixed values of B (Extended Data Fig. 6). The solid lines are quadratic fits.
The fact that only the symmetric contribution persists even in the zero-field limit (Fig. 3a,b) indicates the presence of a finite BCD in the absence of externally applied magnetic fields and thus of a nonlinear Hall effect in time-reversal symmetric conditions. To support the existence of a finite BCD with time-reversal symmetry, we have individually evaluated the dipole originating from the spin-sourced BC and the dipole related to the orbital-sourced BC (Methods). Figure 4a shows that in the entire parameter space of our low-energy theory model, the spin-sourced BCD is two orders of magnitude smaller than the orbital-sourced BCD. The latter exceeds the inverse characteristic Fermi wavenumber \(k_\mathrm{F}^{-1}\) ≈ 0.5 nm. Besides the intrinsic contribution to the BCD, the nonlinear Hall response with time-reversal symmetry also contains disorder-induced contributions10,42 due to nonlinear skew and side-jump scattering. We experimentally access such contributions by measuring the longitudinal signal \({V}_{{{{{yyy}}}}}^{2\omega }\) that is symmetry-allowed but does not possess any intrinsic BCD contribution. As displayed in Fig. 4b, the strong difference in amplitude between the longitudinal signal and transverse \({V}_{{{{{yxx}}}}}^{2\omega }\) signal over a large driving-current range proves the absence of three-fold rotation symmetry as well as a nonlinear Hall effect completely dominated by the intrinsic BCD. The anisotropy between longitudinal and transverse nonlinear signals also allows us to exclude a leading role played by thermoelectric effects due to Joule heating (Fig. 4b, inset). We further observe that both longitudinal \({V}_{{{{{xxx}}}}}^{2\omega }\) and transverse \({V}_{{{{{xyy}}}}}^{2\omega }\) responses have an amplitude comparable with the longitudinal signal \({V}_{{{{{yyy}}}}}^{2\omega }\), thus suggesting their disorder-induced nature. We point out that the finite amplitudes of \({V}_{{{{{xxx}}}}}^{2\omega }\) and \({V}_{{{{{xyy}}}}}^{2\omega }\) imply \({{{{\mathcal{M}}}}}_{\bar{1}10}\) symmetry breaking (Supplementary Note II). This can be related to the mirror-breaking arrangements of the oxygen atoms caused by the antiferrodistortive octahedron rotations.43 It might also be due to the presence of structural domain patterns appearing at the cubic-to-tetragonal structural transition.
a, Calculated spin-sourced and orbital-sourced BCD as a function of the sheet carrier density. The spin-sourced dipole (left) has been evaluated for different strengths of rotational symmetry-breaking distortion (∝vy/vx) (Methods), whereas the orbital-sourced dipole (right) has been computed by varying the strength of orbital Rashba coupling αOR. In both cases, the dipole has a strongly non-monotonic behaviour, goes to zero for large densities and is directed along the \([\bar{1}10]\) direction. The orbital-sourced dipole is two orders of magnitude larger in the entire density range. b, Measured Iω−V2ω characteristics at zero magnetic field. Longitudinal \({V}_{{{{{xxx}}}}({{{{yyy}}}})}^{2\omega }\) and transverse \({V}_{{{{{yxx}}}}({{{{xyy}}}})}^{2\omega }\) voltage drops versus the a.c. excitation bias ∣Iω∣ for \({I}_{{{{{x}}}}({{{{y}}}})}^{\omega }\) along \([\bar{1}10]\) (\([\bar{1}\bar{1}2]\)) at σxx ≈ σyy ≈ 4.5–4.6 mS. The solid lines are quadratic fits. The inset shows the linear two-terminal I–V characteristics highlighting the ohmic behaviour of the electrical contacts to the 2DES. The solid lines are linear fits. c, Sheet conductance dependence of the measured nonlinear transverse-conductivity tensor elements χyxx and χxyy for Iω sourced along the two orthogonal in-plane principal crystallographic directions. d, BCD magnitude Dx under time-reversal symmetric conditions (B = 0). The BCD estimated using equation (1) is found to strongly peak at intermediate-doping levels, where it reaches the maximum value of nearly –75 nm. e, Temperature dependence of the nonlinear transverse conductivities χyxx and χxyy. The two quantities go to zero as the temperature increases and strontium titanate recovers a higher (non-polar tetragonal) crystal symmetry. Concomitantly, the BCD is forced to vanish by symmetry. f, Temperature dependence of BCD Dx (left axis) and the corresponding change in sheet conductance σxx(T) of the 2DES (right axis). The solid and dashed lines in d and f are guides to the eye.
We have systematically verified the occurrence of a sizable nonlinear transverse response over the full range of sheet conductances and concomitantly observed a large difference between the two nonlinear transverse-conductivity tensor component χyxx and χxyy (Fig. 4c). This further proves the main intrinsic BCD contribution to the nonlinear Hall response. By further evaluating the momentum relaxation time τ (Supplementary Note II), we can estimate the size of the BCD (Methods):
The resulting BCD (Fig. 4d) is two orders of magnitude larger than the dipole observed in systems with massive Dirac fermions, such as bilayer WTe2 (refs. 11,12) and—over a finite density range—a factor of two larger than the dipole observed in corrugated bilayer graphene13. We attribute the large magnitude of this effect to the fact that the orbital-sourced BC is naturally equipped with a large dipolar density due to the presence of singular pinch points and hotspots with dipolar arrangements. We also monitored the temperature dependence of transverse-conductivity tensor components χyxx and χxyy (Fig. 4e) and the corresponding behaviour of BCD Dx (Fig. 4f). All these quantities rapidly drop approaching 30 K, that is, the temperature above which the strong polar quantum fluctuations of SrTiO3 vanish. This further establishes the orbital Rashba coupling as the physical mechanism behind the orbital-sourced BC.
The pure orbital-based mechanism of BCD featured here paves the way to the atomic-scale design of quantum sources of nonlinear electrodynamics persisting up to room temperature. Oxide-based 2DES could be, for instance, combined with a room-temperature polar ferroelectric layer, triggering symmetry lowering and thus inducing orbital Rashba coupling by interfacial design. This and other alternative platforms combining a low-symmetry crystal with orbital degrees of freedom and polar modes, including room-temperature polar metals44 and conducting ferroelectric domain walls, are candidate oxide architectures to perform operations such as rectification45 and frequency mixing. Moreover, multiple sources of BC can be implemented for combined optoelectronic and spintronic functionalities in a single-material system: photogalvanic currents due to the orbital-sourced BC can be employed to create spin Hall voltages exploiting the spin-sourced BC. Our study also establishes a general approach to generate topological charge distributions in strongly correlated materials, opening a vast space for exploration at the intersection between topology and correlations.
Methods
Sample growth
The nine-unit-cell-thick LaAlO3 crystalline layer is grown on the TiO-rich surface of a (111)-oriented SrTiO3 substrate, from the ablation of a high-purity (>99.9%) LaAlO3 sintered target by pulsed laser deposition using a KrF excimer laser (wavelength, 248 nm). We perform the real-time monitoring of growth by following intensity oscillations, in a layer-by-layer growth mode, of the first diffraction spot using reflection high-energy electron diffraction (Extended Data Fig. 7a). This allows us to stop the growth at precisely the critical thickness of nine unit cells of LaAlO3 (ref. 46) necessary for the (111)-oriented LaAlO3/SrTiO3 2DES to form. The SrTiO3(111) substrate was first heated to 700 °C in an oxygen partial pressure of 6 × 10−5 mbar. The LaAlO3 layer was grown in those conditions at a laser fluence of 1.2 J cm−2 and laser repetition rate of 1 Hz. Following the growth of the LaAlO3 layer, the temperature is ramped down to 500 °C before performing one-hour-long in situ annealing in a static background pressure of 300 mbar of pure oxygen, to recover the oxygen stoichiometry of the reduced heterostructure. Finally, the sample is cooled down at –20 °C min−1, and kept in the same oxygen environment at zero heating power for at least 45 min.
Device fabrication
The (111)-oriented LaAlO3/SrTiO3 blanket films were lithographically patterned into two Hall bars (width W = 40 μm; length L = 180 μm), oriented along the two orthogonal crystal-axis directions of \([\bar{1}10]\) and \([\bar{1}\bar{1}2]\). The Hall bars are defined by electron-beam lithography into a poly(methyl methacrylate) resist, which is used as a hard mask for argon-ion milling (Extended Data Fig. 7c). The dry-etching duration is calibrated and timed to be precisely stopped when the LaAlO3 layer is fully removed to avoid the creation of an oxygen-deficient conducting SrTiO3−δ surface. This leaves an insulating SrTiO3 matrix surrounding the protected LaAlO3/SrTiO3 areas, which host a geometrically confined 2DES.
Electrical transport measurements
The Hall bars are connected to a chip carrier by an ultrasonic wedge-bonding technique in which the aluminium wires form ohmic contacts with the 2DES through the LaAlO3 overlayer. The sample is anchored to the chip carrier by homogeneously coating the backside of the SrTiO3 substrate with silver paint. A d.c. voltage Vg is sourced between the silver back-electrode and the desired Hall-bar device to enable electrostatic-field-effect gating of the 2DES, leveraging the large dielectric permittivity of strontium titanate at low T (~2 × 104 below 10 K)47,48. Non-hysteretic dependence of σxx (σyy) on Vg is achieved following an initial gate-forming procedure49.
Standard four-terminal electrical (magneto-)transport measurements were performed at 1.5 K in a liquid helium-4 flow cryostat, equipped with a superconducting magnet (maximum magnetic field, B = ±12 T). An a.c. excitation current Iω ∝ |Iω|sin(ωt), of frequency ω/(2π) = 17.77 Hz, is sourced along the desired crystallographic direction. The sheet resistance, \({R}_{{{{\rm{s}}}}}={\sigma }_{{{{{xx}}}}}^{-1}\), of a Hall-bar device is related to the first-harmonic longitudinal voltage drop Vxx according to Rs = (Vxx/Ix)(W/L). When the a.c. current is sourced along \(\hat{{{{\bf{x}}}}}\parallel [\bar{1}10]\) (\(\hat{{{{\bf{y}}}}}\parallel [\bar{1}\bar{1}2]\)), we make use of a standard lock-in detection technique to concomitantly measure the first-harmonic longitudinal response Vxx (Vyy), and either the in-phase first-harmonic \({V}_{{{{{xy}}}}}^{\omega }\) (\({V}_{{{{{yx}}}}}^{\omega }\)) or out-of-phase second-harmonic \({V}_{{{{{yxx}}}}}^{2\omega }\) (\({V}_{{{{{xyy}}}}}^{2\omega }\)) transverse voltages (Fig. 1a). We define the first- and second-harmonic transverse resistances as \({R}_{{{{{xy}}}}}^{\omega }={V}_{{{{{xy}}}}}^{\omega }/| {I}_{{{{{x}}}}}^{\omega }|\) and \({R}_{{{{{y}}}}}^{2\omega }={V}_{{{{{yxx}}}}}^{2\omega }/| {I}_{{{{{x}}}}}^{\omega }{| }^{2}\), respectively. First- and second-harmonic measurements are performed at 10 and 50 μA, respectively.
We systematically decompose both first- and second-harmonic magneto-responses into their field-symmetric \({R}_{{{{\rm{sym}}}}}^{(2)\omega }\) and field-antisymmetric \({R}_{{{{\rm{as}}}}}^{(2)\omega }\) contributions according to
In particular, the first-harmonic transverse resistance is purely field antisymmetric, and hence, we chose the simplified notation of \({R}_{{{{{xy}}}}}\equiv {R}_{{{{{xy}}}},{{{\rm{as}}}}}^{\omega }\).
Estimation of the Rashba spin–orbit energy from magnetoconductance measurements in the weak antilocalization regime
In a 2DES, in the presence of a spin relaxation mechanism induced by an additional spin–orbit interaction, the conductance is subject to weak localization corrections at lower temperatures. Extended Data Fig. 4a shows the gate-modulated magnetoconductance curves of the 2DES, which exhibit a characteristic low-field weak antilocalization behaviour. The magnetoconductance curves, normalized to the quantum of conductance GQ = e2/(πħ), are fitted using a Hikami–Larkin–Nagaoka model that expresses the change in conductivity Δσ(B⟂) = σ(B⟂) – σ(0) of the 2DES under an external out-of-plane magnetic field B⊥, in the diffusive regime (with negligible Zeeman splitting), as follows50,51:
where Ψ is the digamma function; ħ = h/(2π) is the reduced Planck constant; \({B}_{{{{\rm{i}}}},{{{\rm{so}}}}}=\hslash /\left(4eD{\tau }_{{{{\rm{i}}}},{{{\rm{so}}}}}\right)\) are the effective fields related to the inelastic and spin–orbit relaxation times (τi and τso, respectively); and D = πħ2σ(0)/(e2m*) is the diffusion constant. The last term in equation (3), proportional to \({B}_{\perp }^{2}\), contains AK, the so-called Kohler coefficient, which accounts for orbital magnetoconductance.
Hence, from the fit to the weak antilocalization magnetoconductance curves, the effective Rashba spin–orbit coupling αR can be calculated as
based on a D’yakonov–Perel’ spin relaxation mechanism51. A summary of the dependence of the extracted parameters on the 2DES’ sheet conductance is plotted in Extended Data Fig. 5b. The spin–orbit energy Δso can then be estimated according to
where, in two dimensions, the Fermi wavevector is given by \({k}_{{{{\rm{F}}}}}=\sqrt{2\uppi {n}_{2{{{\rm{D}}}}}}\), assuming a circular Fermi surface. The sheet carrier density n2D is experimentally obtained for each doping value from the (ordinary) Hall effect (Supplementary Note III), measured concomitantly with the magnetoconductance traces.
Spin-sourced and orbital-sourced BCD calculations
We first estimate the BCD due to spin sources in time-reversal symmetry condition as a function of carrier density considering the low-energy Hamiltonian for a single Kramers’-related pair of bands (Supplementary Note I):
where the momentum-dependent mass can be negative close to the Γ point (Supplementary Note I). Although this model Hamiltonian is equipped with a finite BC, its dipole is forced to vanish by the three-fold rotation symmetry (Supplementary Note I). We capture the rotation symmetry breaking of the low-temperature structure at the leading order by assuming inequivalent coefficients for the spin–orbit coupling terms linear in momentum. In other words, we make the substitution αR(σxky – σykx)→vykyσx – vxkxσy. Since the dipole is a pseudo-vector, the residual mirror symmetry \({{{{\mathcal{M}}}}}_{x}\) forces it to be directed along the \(\hat{{{{\bf{x}}}}}\) direction. In the relaxation-time approximation, it is given by
where Ωz is the BC of our two-band model that we write in a dimensionless form by measuring energies in units of \({k}_{{{{\rm{F}}}}}^{2}/2m({k}_{{{{\rm{F}}}}})\), lengths in units of 1/kF and densities in units of \({n}_{0}={k}_{{{{\rm{F}}}}}^{2}/2\uppi\). Here kF is a reference Fermi wavevector. For simplicity, we have considered a positive momentum-independent effective mass. For the BCD shown in Fig. 4a, the remaining parameters have been chosen as vx = 0.4, vy = (1.2, 1.4, 1.6) × vx and λ = 0.1. Moreover, we account for orbital degeneracy by tripling the dipole of a single Kramers’ pair. This gives an upper bound for the spin-sourced BCD.
We have also evaluated the BCD due to orbital sources considering the low-energy Hamiltonian for spin–orbit-free t2g electrons derived from symmetry principles (Supplementary Note I) and reading
where we introduced the Gell–Mann matrices as
and Λ0 is the identity matrix. In the Hamiltonian above, Δ is the splitting between the a1g singlet and \({e}_{\mathrm{g}}^{{\prime} }\) doublet resulting from the t2g orbitals in a trigonal crystal field. Here Δm is the additional splitting between the doublet caused by rotational symmetry breaking. Finally, αOR and αm are the strengths of the orbital Rashba coupling. Note that in the presence of three-fold rotation symmetry, αm ≡ 0, in which case the BC is forced to vanish. For simplicity, we have evaluated the BC for the \({{{{\mathcal{C}}}}}_{\mathrm{s}}\) point group-symmetric case assuming αm ≡ αOR. In our continuum SU(3) model, the BC can be computed using the method outlined elsewhere52. We have subsequently computed the corresponding dipole measuring, as before, energies in units of \({k}_{{{{\rm{F}}}}}^{2}/2m\), lengths in units of 1/kF and densities in units of \({n}_{0}={k}_{{{{\rm{F}}}}}^{2}/2\uppi\). The dimensionless orbital Rashba coupling has been varied between αOR = 1 and αOR = 2, whereas we have fixed Δ = –0.1 and Δm = 0.005. The value of the crystal field splitting Δ is consistent with the amplitude determined by X-ray absorption spectroscopy53 of the order 8 meV, and therefore, it is almost one order of magnitude smaller than our energy unit of ~40 meV for a reference \({k}_{\mathrm{F}}^{-1}\) ≃ 0.5 nm and effective mass m ≃ 3me (Supplementary Note III). The calculated dipole (Fig. 4a) has been finally multiplied by two to account for spin degeneracy. As shown in Supplementary Note I, we remark that the model Hamiltonian for the spin sources of BC (equation (6)) and the model Hamiltonian for the orbital sources (equation (8)) derive from a single six-band model where orbital and spin degrees of freedom are treated on an equal footing.
Estimation of BCD magnitude from nonlinear Hall measurements
The nonlinear current density is mathematically given by \({j}_{\alpha }^{2\omega }={\chi }_{\alpha \beta \gamma }\,{E}_{\beta }\,{E}_{\gamma }\), where χαβγ is the nonlinear transverse-conductivity tensor. When an a.c. current density \({I}_{{{{{x}}}}}^{\omega }/W={\sigma }_{{{{{xx}}}}}{E}_{{{{{x}}}}}^{\omega }\) is sourced along \(\hat{{{{\bf{x}}}}}\), the second-harmonic transverse current density developing along \(\hat{{{{\bf{y}}}}}\) is related to the BCD D according to9
where τ is the momentum relaxation time and e is the elementary charge. Due to the mirror symmetry \({{{{\mathcal{M}}}}}_{{{{{x}}}}}\equiv {{{{\mathcal{M}}}}}_{[\bar{1}10]}\), the dipole is found to point along \(\hat{{{{\bf{x}}}}}\); in the quasi-d.c. limit, that is, (ωτ) ≪ 1, the BCD expression reduces to
which is the explicit expression for equation (1), in terms of experimentally measurable quantities only, and where
are the measured nonlinear transverse-conductivity tensor elements shown in Fig. 4c,e.
Data availability
The data that support the findings of this study are available via Zenodo at https://doi.org/10.5281/zenodo.7575479.
Code availability
The code that support the findings of the study is available from the corresponding authors on reasonable request.
References
Haldane, F. D. M. Berry curvature on the Fermi surface: anomalous Hall effect as a topological Fermi-liquid property. Phys. Rev. Lett. 93, 206602 (2004).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
He, P. et al. Quantum frequency doubling in the topological insulator Bi2Se3. Nat. Commun. 12, 698 (2021).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Battilomo, R., Scopigno, N. & Ortix, C. Anomalous planar Hall effect in two-dimensional trigonal crystals. Phys. Rev. Research 3, L012006 (2021).
Cullen, J. H., Bhalla, P., Marcellina, E., Hamilton, A. R. & Culcer, D. Generating a topological anomalous Hall effect in a nonmagnetic conductor: an in-plane magnetic field as a direct probe of the Berry curvature. Phys. Rev. Lett. 126, 256601 (2021).
Sodemann, I. & Fu, L. Quantum nonlinear Hall effect induced by Berry curvature dipole in time-reversal invariant materials. Phys. Rev. Lett. 115, 216806 (2015).
Ortix, C. Nonlinear Hall effect with time-reversal symmetry: theory and material realizations. Adv. Quantum Technol. 4, 2100056 (2021).
Xu, S.-Y. et al. Electrically switchable Berry curvature dipole in the monolayer topological insulator WTe2 .Nat. Phys. 14, 900–906 (2018).
Ma, Q. et al. Observation of the nonlinear Hall effect under time-reversal-symmetric conditions. Nature 565, 337–342 (2019).
Ho, S.-C. et al. Hall effects in artificially corrugated bilayer graphene without breaking time-reversal symmetry. Nat. Electron. 4, 116–125 (2021).
Battilomo, R., Scopigno, N. & Ortix, C. Berry curvature dipole in strained graphene: a Fermi surface warping effect. Phys. Rev. Lett. 123, 196403 (2019).
You, J.-S., Fang, S., Xu, S.-Y., Kaxiras, E. & Low, T. Berry curvature dipole current in the transition metal dichalcogenides family. Phys. Rev. B 98, 121109 (2018).
Son, J., Kim, K.-H., Ahn, Y. H., Lee, H.-W. & Lee, J. Strain engineering of the Berry curvature dipole and valley magnetization in monolayer MoS2. Phys. Rev. Lett. 123, 036806 (2019).
Zhang, Y., van den Brink, J., Felser, C. & Yan, B. Electrically tuneable nonlinear anomalous Hall effect in two-dimensional transition-metal dichalcogenides WTe2 and MoTe2. 2D Mater. 5, 044001 (2018).
Du, Z. Z., Wang, C. M., Lu, H.-Z. & Xie, X. C. Band signatures for strong nonlinear Hall effect in bilayer WTe2. Phys. Rev. Lett. 121, 266601 (2018).
Kang, K., Li, T., Sohn, E., Shan, J. & Mak, K. Nonlinear anomalous Hall effect in few-layer WTe2. Nat. Mater. 18, 324–328 (2019).
Kumar, D. et al. Room-temperature nonlinear Hall effect and wireless radiofrequency rectification in Weyl semimetal TaIrTe4. Nat. Nanotechnol. 16, 421–425 (2021).
Matsyshyn, O. & Sodemann, I. Nonlinear Hall acceleration and the quantum rectification sum rule. Phys. Rev. Lett. 123, 246602 (2019).
Singh, S., Kim, J., Rabe, K. M. & Vanderbilt, D. Engineering Weyl phases and nonlinear Hall effects in Td-MoTe2. Phys. Rev. Lett. 125, 046402 (2020).
Facio, J. I. et al. Strongly enhanced Berry dipole at topological phase transitions in BiTeI. Phys. Rev. Lett. 121, 246403 (2018).
Zhang, Y., Sun, Y. & Yan, B. Berry curvature dipole in Weyl semimetal materials: an ab initio study. Phys. Rev. B 97, 041101 (2018).
Wawrzik, D., You, J.-S., Facio, J. I., van den Brink, J. & Sodemann, I. Infinite Berry curvature of Weyl Fermi arcs. Phys. Rev. Lett. 127, 056601 (2021).
Ohtomo, A. & Hwang, H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007).
Rout, P. K., Maniv, E. & Dagan, Y. Link between the superconducting dome and spin-orbit interaction in the (111) LaAlO3/SrTiO3 interface. Phys. Rev. Lett. 119, 237002 (2017).
Monteiro, A. M. R. V. L. et al. Two-dimensional superconductivity at the (111)LaAlO3/SrTiO3 interface. Phys. Rev. B 96, 020504 (2017).
Monteiro, A. M. R. V. L. et al. Band inversion driven by electronic correlations at the (111) LaAlO3/SrTiO3 interface. Phys. Rev. B 99, 201102 (2019).
Rödel, T. C. et al. Orientational tuning of the Fermi sea of confined electrons at the SrTiO3 (110) and (111) surfaces. Phys. Rev. Applied 1, 051002 (2014).
Bareille, C. et al. Two-dimensional electron gas with six-fold symmetry at the (111) surface of KTaO3. Sci. Rep. 4, 3586 (2014).
Fu, L. Hexagonal warping effects in the surface states of the topological insulator Bi2Te3. Phys. Rev. Lett. 103, 266801 (2009).
He, P. et al. Observation of out-of-plane spin texture in a SrTiO3(111) two-dimensional electron gas. Phys. Rev. Lett. 120, 266802 (2018).
Trama, M., Cataudella, V., Perroni, C. A., Romeo, F. & Citro, R. Gate tunable anomalous Hall effect: Berry curvature probe at oxides interfaces. Phys. Rev. B 106, 075430 (2022).
Kim, B. et al. Microscopic mechanism for asymmetric charge distribution in Rashba-type surface states and the origin of the energy splitting scale. Phys. Rev. B 88, 205408 (2013).
Mercaldo, M. T., Noce, C., Caviglia, A. D., Cuoco, M. & Ortix, C. Orbital design of Berry curvature: pinch points and giant dipoles induced by crystal fields. npj Quantum Mater. 8, 12 (2023).
Rimai, L. & deMars, G. A. Electron paramagnetic resonance of trivalent gadolinium ions in strontium and barium titanates. Phys. Rev. 127, 702–710 (1962).
Fleury, P. A., Scott, J. F. & Worlock, J. M. Soft phonon modes and the 110°K phase transition in SrTiO3. Phys. Rev. Lett. 21, 16–19 (1968).
Rössle, M. et al. Electric-field-induced polar order and localization of the confined electrons in LaAlO3/SrTiO3 heterostructures. Phys. Rev. Lett. 110, 136805 (2013).
Onsager, L. Reciprocal relations in irreversible processes. I. Phys. Rev. 37, 405–426 (1931).
Du, Z. Z., Wang, C. M., Li, S., Lu, H.-Z. & Xie, X. C. Disorder-induced nonlinear Hall effect with time-reversal symmetry. Nat. Commun. 10, 3047 (2019).
Salje, E. K. H., Aktas, O., Carpenter, M. A., Laguta, V. V. & Scott, J. F. Domains within domains and walls within walls: evidence for polar domains in cryogenic SrTiO3. Phys. Rev. Lett. 111, 247603 (2013).
Kim, T. H. et al. Polar metals by geometric design. Nature 533, 68–72 (2016).
Zhang, Y. & Fu, L. Terahertz detection based on nonlinear Hall effect without magnetic field. Proc. Natl Acad. Sci. USA 118, e2100736118 (2021).
Herranz, G., Sánchez, F., Dix, N., Scigaj, M. & Fontcuberta, J. High mobility conduction at (110) and (111) LaAlO3/SrTiO3 interfaces. Sci. Rep. 2, 758 (2012).
Müller, K. A. & Burkard, H. SrTiO3: an intrinsic quantum paraelectric below 4 K. Phys. Rev. B 19, 3593–3602 (1979).
Thiel, S., Hammerl, G., Schmehl, A., Schneider, C. W. & Mannhart, J. Tunable quasi-two-dimensional electron gases in oxide heterostructures. Science 313, 1942–1945 (2006).
Biscaras, J. et al. Limit of the electrostatic doping in two-dimensional electron gases of LaXO3(X = Al, Ti)/SrTiO3. Sci. Rep. 4, 6788 (2014).
Hikami, S., Larkin, A. I. & Nagaoka, Y. Spin-orbit interaction and magnetoresistance in the two dimensional random system. Prog. Theor. Phys. 63, 707–710 (1980).
Maekawa, S. & Fukuyama, H. Magnetoresistance in two-dimensional disordered systems: effects of Zeeman splitting and spin-orbit scattering. J. Phys. Soc. Jpn 50, 2516–2524 (1981).
Barnett, R., Boyd, G. R. & Galitski, V. Su(3) spin-orbit coupling in systems of ultracold atoms. Phys. Rev. Lett. 109, 235308 (2012).
De Luca, G. M. et al. Symmetry breaking at the (111) interfaces of SrTiO3 hosting a two-dimensional electron system. Phys. Rev. B 98, 115143 (2018).
Acknowledgements
This work was supported by the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract no. MB22.00071, the Gordon and Betty Moore Foundation (grant no. 332 GBMF10451 to A.D.C.), the European Research Council (ERC) (grant no. 677458), by the project Quantox of QuantERA ERA-NET Cofund in Quantum Technologies, and by the Netherlands Organisation for Scientific Research (NWO/OCW) as part of the VIDI (project 680-47-543 to C.O. and project 016.Vidi.189.061 to A.D.C.), the ENW-GROOT (project TOPCORE) program (to A.D.C. and U.F.) and Frontiers of Nanoscience program (NanoFront). E.L. acknowledges funding from the EU Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 707404. We acknowledge A. M. Monteiro, L. Hendl, J. R. Hortensius, P. Bruneel and M. Gabay for valuable discussions.
Funding
Open access funding provided by University of Geneva.
Author information
Authors and Affiliations
Contributions
A.D.C. proposed and supervised the experiments. C.O. proposed the theory models and supervised their analysis. E.L. grew the crystalline LaAlO3 thin films by pulsed laser deposition and performed the structural characterizations. E.L. and Y.G.S. lithographically patterned the samples, performed the magnetotransport experiments and analysed the experimental data with help from T.C.v.T. and U.F. R.B. and M.T.M. performed the BC and semiclassical transport calculations with help from M.C., C.N. and C.O. C.O., E.L., R.B. and A.D.C. wrote the manuscript, with input from all the authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Materials thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Hall effect in a planar magnetic field.
Experimentally measured field-antisymmetric transverse magnetoresistance \({R}_{{{{\rm{yx}}}}}={V}_{{{{\rm{yx}}}}}^{\omega }/{I}_{{{{\rm{y}}}}}^{\omega }\) at T = 1.5 K, with \({I}_{{{{\rm{x}}}}}^{\omega }\) along \([\bar{1}10]\perp B\) (see inset schematic), for varying sheet conductance values σxx (indicated by the inset colored scale bar), and tuned via electrostatic field effect in a back-gate geometry.
Extended Data Fig. 2 Nonlinear Hall response in a planar magnetic field.
Experimentally measured field-symmetric nonlinear transverse magnetoresponse \({R}_{{{{\rm{x}}}}}^{2\omega }\) at T = 1.5 K with \({I}_{{{{\rm{y}}}}}^{\omega }\) along \([\bar{1}\bar{1}2]\perp B\) (see inset schematic), for varying sheet conductance values σyy (indicated by the inset colored scale bar). The full scale ordinate axis is chosen to be the same as for panel b of Fig. 3, for better comparison, and highlights the comparatively small nonlinear Hall response when the current is sourced along the \({{{{\mathcal{M}}}}}_{\bar{1}10}\) mirror line corresponding to a symmetry demanded zero BCD.
Extended Data Fig. 3 Temperature dependence of the Hall and longitudinal magnetoresistances in a planar magnetic field.
Temperature dependent planar Hall resistance (a,c) and longitudinal MR (b,d) in the linear response regime for various strength of the in-plane magnetic field (and at fixed gate-voltage), with \({I}_{{{{\rm{y}}}}}^{\omega }\) along \([\bar{1}\bar{1}2]\parallel B\) (a-b) and \({I}_{{{{\rm{x}}}}}^{\omega }\) along \([\bar{1}10]\perp B\) (c-d). Both Ryx and Rxy, as well as the corresponding longitudinal MR, asymptotically go to zero as the temperature increases toward strontium titanate’s nonpolar tetragonal phase (above ≈ 30 K).
Extended Data Fig. 4 Weak antilocalization regime and Rashba spin-orbit coupling.
a, Gate-modulated magnetoconductance curves (normalized to the quantum of conductance GQ) for \({I}_{{{{\rm{x}}}}}^{\omega }\) along \([\bar{1}10]\) (see also Supplementary Note III for WAL measurements along \([\bar{1}\bar{1}2]\)). Hikami-Larkin-Nagaoka fits (solid red lines) are performed following Eq. (3). B⊥, the out-of-plane magnetic field. (c) Left axis: Experimentally estimated momentum, inelastic and spin-orbit relaxation times, τel (named τ throughout the manuscript), τi and τso, respectively. Right axis: Strength of the Rashba spin-orbit coupling αR versus sheet conductance σxx.
Extended Data Fig. 5 Effective Zeeman energy and Rashba spin-orbit energy of the 2DES.
a-b, Right axis: Sheet conductance dependence of the Rashba spin-orbit energy Δso/2 = αRkF and effective Zeeman energy \({\Delta }_{{{{\rm{Z}}}}}^{{{{\rm{c}}}}}=g{\mu }_{{{{\rm{B}}}}}{B}^{{{{\rm{c}}}}}/2\) at the critical in-plane field Bc (left axis), for \({I}_{{{{\rm{x}}}}}^{\omega }\) along \([\bar{1}10]\) (panel a) and for \({I}_{{{{\rm{y}}}}}^{\omega }\) along \([\bar{1}\bar{1}2]\) (panel b). See Supplementary Note III for details regarding the determination of Bc.
Extended Data Fig. 6 Current bias dependent nonlinear transverse signal in a planar magnetic field.
a,b, Field-antisymmetric, \({R}_{{{{\rm{y}}}},{{{\rm{as}}}}}^{2\omega }\), and field-symmetric \({R}_{{{{\rm{y,sym}}}}}^{2\omega }\) second harmonic transverse resistance responses, for various magnitudes of the excitation a.c. current along \([\bar{1}10]\) (∥B, see inset schematic).
Extended Data Fig. 7 Growth, structural characterization and device fabrication of (111)-oriented LaAlO3/SrTiO3 2DES.
a, In situ real-time RHEED monitoring of the layer-by-layer PLD growth of a 9 u.c. LaAlO3 film on a (111)-oriented SrTiO3 substrate. Insets: RHEED patterns acquired before (left) and after the film growth (right), highlighting the high crystalline quality of the epitaxial LaAlO3 film. The vertical arrow marks the end of the growth (at 245 s). b, Atomic force microscopy image of a 9 u.c. thick LaAlO3 film on SrTiO3(111). The film’s topography reproduces the characteristic atomically sharp steps-and-terraces structure of the substrate’s vicinal surface. Horizontal scale bar: 1 μm. c, Optical micrograph of a patterned PPMA resist hard mask on a 9 u.c. blanket film of LaAlO3/SrTiO3 (before the Ar ion milling step) which ultimately defines the Hall bar device area where the 2DES subsists. Pre-patterned gold markers are used to signify the position of the Hall bars’ contact pads, as the optical contrast between the etched area (bare substrate) and the crystalline LaAlO3/SrTiO3 devices is extremely low. Scale bar: 200 μm.
Supplementary information
Supplementary Information
Supplementary Notes I–III and Figs. 1–14.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lesne, E., Saǧlam, Y.G., Battilomo, R. et al. Designing spin and orbital sources of Berry curvature at oxide interfaces. Nat. Mater. 22, 576–582 (2023). https://doi.org/10.1038/s41563-023-01498-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-023-01498-0
This article is cited by
-
Light-induced giant enhancement of nonreciprocal transport at KTaO3-based interfaces
Nature Communications (2024)
-
A tunable room-temperature nonlinear Hall effect in elemental bismuth thin films
Nature Electronics (2024)
-
Observation of the orbital inverse Rashba–Edelstein effect
Nature Physics (2023)