Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Dual-density waves with neutral and charged dipolar excitons of GaAs bilayers

Nature Materials volume 22, pages 170–174 (2023)Cite this article

Subjects

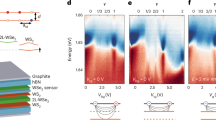
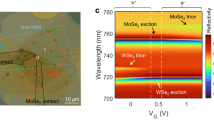
Abstract

Strongly correlated quantum particles in lattice potentials are the building blocks for a wide variety of quantum insulators—for instance, Mott phases and density waves breaking lattice symmetry1,2,3. Such collective states are accessible to bosonic and fermionic systems2,4,5,6,7,8,9,10,11,12. To expand further the spectrum of accessible quantum matter phases, mixing both species is theoretically appealing because density order then competes with phase separation13,14,15,16. Here we manipulate such a Bose–Fermi mixture by confining neutral (boson-like) and charged (fermion-like) dipolar excitons in an artificial square lattice of a GaAs bilayer. At unitary lattice filling, strong inter- and intraspecies interactions stabilize insulating phases when the fraction of charged excitons is around (1/3, 1/2, 2/3). We evidence that dual Bose–Fermi density waves are then realized, with species ordered in alternating stripes. Our observations highlight that dipolar excitons allow for controlled implementations of Bose–Fermi Hubbard models extended by off-site interactions.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Neutral and charged excitons’ Bose–Fermi mixture.
Fig. 2: Charged exciton insulators at unity and half fillings.
Fig. 3: Dual-density waves of neutral and charged excitons.

Similar content being viewed by others

Data availability

Source data are available for download, together with the published manuscript.

References

  1. Salomon, C., Shlyapnikov, G. V. & Cugliandolo, L. F. Many-Body Physics with Ultracold Gases (Oxford Univ. Press, 2012).

  2. Arovas, D. P., Berg, E., Kivelson, S. A. & and Raghu, S. The Hubbard Model. Annu. Rev. Condens. Matter Phys. https://doi.org/10.1146/annurev-conmatphys-031620-102024 (2022).

  3. Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Colloquium: theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457 (2015).

    Article  CAS  Google Scholar 

  4. Greiner, M., Mandel, O., Esslinger, T., Haensch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2002).

    Article  CAS  Google Scholar 

  5. Gemelke, N., Zhang, X., Hung, C. L. & Chin, C. In situ observation of incompressible Mott-insulating domains in ultracold atomic gases. Nature 460, 995–998 (2009).

    Article  CAS  Google Scholar 

  6. Li, H. et al. Imaging two-dimensional generalized Wigner crystals. Nature 597, 650–654 (2021).

    Article  CAS  Google Scholar 

  7. Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).

    Article  CAS  Google Scholar 

  8. Huang, X. et al. Correlated insulating states at fractional fillings of the WS2/WSe2 moiré‚ lattice. Nat. Phys. 17, 715–719 (2021).

    Article  CAS  Google Scholar 

  9. Xu, Y. et al. Correlated insulating states at fractional fillings of moiré superlattices. Nature 587, 214–218 (2020).

    Article  CAS  Google Scholar 

  10. Jin, C. et al. Stripe phases in WSe2/WS2 moiré‚ superlattices. Nat. Mater. 20, 940–944 (2021).

    Article  CAS  Google Scholar 

  11. Lagoin, C., Suffit, S., Baldwin, K., Pfeiffer, L. & Dubin, F. Mott insulator of strongly interacting two-dimensional excitons. Nat. Phys. 18, 149–153 (2022).

    Article  CAS  Google Scholar 

  12. Lagoin, C. et al. Extended Bose-Hubbard model with dipolar excitons. Nature 609, 485–489 (2022).

    Article  CAS  Google Scholar 

  13. Büchler, H. P. & Blatter, G. Supersolid versus phase separation in atomic Bose-Fermi mixtures. Phys. Rev. Lett. 91, 130404 (2003).

    Article  Google Scholar 

  14. Lewenstein, M., Santos, L., Baranov, M. A. & Fehmann, H. Atomic Bose-Fermi mixtures in an optical lattice. Phys. Rev. Lett. 92, 050401 (2004).

    Article  CAS  Google Scholar 

  15. Titvinidze, I., Snoek, M. & Hofstetter, W. Supersolid Bose-Fermi mixtures in optical lattices. Phys. Rev. Lett. 100, 100401 (2008).

    Article  CAS  Google Scholar 

  16. Sugawa, S. et al. Interaction and filling-induced quantum phases of dual Mott insulators of bosons and fermions. Nat. Phys. 7, 642–648 (2011).

    Article  Google Scholar 

  17. Combescot, M., Combescot, R. & Dubin, F. Bose-Einstein condensation of indirect excitons: a review. Rep. Prog. Phys. 80, 066401 (2017).

    Article  Google Scholar 

  18. Remeika, M., Fogler, M. M., Butov, L. V., Hanson, M. & Gossard, A. C. Two-dimensional electrostatic lattices for indirect excitons. Appl. Phys. Lett. 100, 061103 (2012).

    Article  Google Scholar 

  19. Lagoin, C. et al. Microscopic lattice for two-dimensional dipolar excitons. Phys. Rev. B 102, 245428 (2020).

    Article  CAS  Google Scholar 

  20. Baranov, M. A., Dalmonte, M., Pupillo, G. & Zoller, P. Condensed matter theory of dipolar quantum gases. Chem. Rev. 112, 5012–5061 (2012).

    Article  CAS  Google Scholar 

  21. Dutta, O. et al. Non-standard Hubbard models in optical lattices: a review. Rep. Prog. Phys. 78, 066001 (2015).

    Article  Google Scholar 

  22. Beian, M. et al. Spectroscopic signatures for the dark Bose-Einstein condensation of spatially indirect excitons. Europhys. Lett. 119, 37004 (2017).

    Article  Google Scholar 

  23. Dietl, S. et al. On the parabolicity of dipolar exciton traps and their population of excess charge carriers. New J. Phys. 21, 063028 (2019).

    Article  CAS  Google Scholar 

  24. Misra, S. et al. The role of spin-flip collisions in a dark-exciton condensate. Proc. Natl Acad. Soc. USA 119, e2203531119 (2022).

    Article  CAS  Google Scholar 

  25. Sergeev, R. & Suris, R. A. The X+ trion in a system with spatial separation of the charge carriers. Semiconductors 37, 1205–1210 (2003).

    Article  Google Scholar 

  26. Witham, O., Hunt, R. J. & Drummond, N. D. Stability of trions in coupled quantum wells modeled by two-dimensional bilayers. Phys. Rev. B 97, 075424 (2018).

    Article  CAS  Google Scholar 

  27. Chung, Y. J. et al. Ultra-high-quality two-dimensional electron systems. Nat. Mater. 20, 632–637 (2021).

    Article  CAS  Google Scholar 

  28. Kowalik Seidel, K. et al. Tunable photo-emission from an excitonic anti-trap. Nano Lett. 12, 326–330 (2012).

    Article  Google Scholar 

  29. Rapaport, R. & Chen, G. Experimental methods and analysis of cold and dense dipolar exciton fluids. J. Phys. Condens. Matter 19, 295207 (2007).

    Article  Google Scholar 

  30. Schmid, G., Todo, S., Troyer, M. & Dorneich, A. Finite-temperature phase diagram of hard-core Bosons in two dimensions. Phys. Rev. Lett. 88, 167208 (2002).

    Article  Google Scholar 

Download references

Acknowledgements

Research at CNRS (C.L. and F.D.) has been financially supported by IXTASE from the French Agency for Research (no. ANR-20-CE30-0032-01). The work at Princeton University (L.P. and K.B.) was funded in part by the Gordon and Betty Moore Foundation’s EPiQS Initiative (grant no. GBMF9615 to L.P.) and by the National Science Foundation MRSEC (grant no. DMR 2011750) to Princeton University.

Author information

Authors and Affiliations

  1. Institut des Nanosciences de Paris, CNRS and Sorbonne Université, Paris, France

    Camille Lagoin & François Dubin

  2. Laboratoire de Materiaux et Phenomenes Quantiques, Universite Paris Diderot, Paris, France

    Stephan Suffit

  3. PRISM, Princeton Institute for the Science and Technology of Materials, Princeton University, Princeton, NJ, USA

    Kirk Baldwin & Loren Pfeiffer

  4. Université Côte d’Azur – CNRS, CRHEA, Valbonne, France

    François Dubin

Authors
  1. Camille Lagoin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stephan Suffit
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kirk Baldwin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Loren Pfeiffer
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. François Dubin
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

K.B. and L.P. realized the GaAs bilayer while C.L., S.S. and F.D. fabricated the gate electrodes imprinting the 250-nm-period electrostatic lattice. C.L. and F.D. performed all experiments and data analysis and wrote the manuscript. F.D. designed the project.

Corresponding author

Correspondence to François Dubin.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Materials thanks David Ruiz-Tijerina and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Lattice filling vs. gate voltage.

a Total integrated intensities of the PL radiated by neutral and charged excitons, as a function of Vg and at unitary filling (P=14 nW). b Same experimental results as in a but expressed as a function of νCX. c Scaling of νCX as a function of Vg deduced from the measurements shown in a and b. The line provides a guide for the eyes. Experiments were all realised at 330 mK and acquired during four different experimental runs so that detection efficiencies are close but not identical. Vertical error bars display the poissonian precision in a-b and the ± 0.03 precision on νCX in c. In a-c, the horizontal error is smaller than the points size while in b it corresponds to the precision when extracting νCX.

Source data

Extended Data Fig. 2 Evaluation of the residual doping level.

PL spectrum radiated by neutral dipolar excitons for νX ≈ 1/2 (at νCX ≈ 0). The spectrum is measured by averaging 10 realisations performed under unchanged conditions. The profile is given by our spectral resolution, that is reproduced by a single lorentzian-like line with around 150 μeV full-width-at-half-maximum (blue area and black line). Measurements were performed at 330 mK, error bars displaying the level of poissonian fluctuations.

Source data

Extended Data Fig. 3 Thermal melting of CX insulators at νCX = 1/2 and 1.

a Compressibility κCX normalised to the level given by poissonian noise for (νCX = 1/2, νX ≈ 0) as a function of the bath temperature. b Identical measurements for (νCX = 1, νX ≈ 0) . While in a the thermal melting of the insulating phase occurs around 1K, as expected for the magnitude measured for VCX,CX, a similar critical temperature is found in b for the Mott phase. This possibly reflects fluctuations of the density of injected holes while the bath temperature is increased. For all measurements error bars mark our statistical precision when computing the compressibility ( ± 0.03).

Source data

Extended Data Fig. 4 Interaction energies and spatial ordering.

Possible configurations of incompressible phases made by neutral (blue) and charged (red) excitons. The respective energy shifts of PL energies, EX and ECX, are indicated below each configuration together with the resulting magnitude of ΔEX,CX, by only taking into account NN interactions.

Source data

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lagoin, C., Suffit, S., Baldwin, K. et al. Dual-density waves with neutral and charged dipolar excitons of GaAs bilayers. Nat. Mater. 22, 170–174 (2023). https://doi.org/10.1038/s41563-022-01409-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41563-022-01409-9

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing