Abstract
Topological theories have established a unique set of rules that govern the transport properties in a wide variety of wave-mechanical settings. In a marked departure from the established approaches that induce Floquet topological phases by specifically tailored discrete coupling protocols or helical lattice motions, we introduce a class of bimorphic Floquet topological insulators that leverage connective chains with periodically modulated on-site potentials to reveal rich topological features in the system. In exploring a ‘chain-driven’ generalization of the archetypical Floquet honeycomb lattice, we identify a rich phase structure that can host multiple non-trivial topological phases associated simultaneously with both Chern-type and anomalous chiral states. Experiments carried out in photonic waveguide lattices reveal a strongly confined helical edge state that, owing to its origin in bulk flat bands, can be set into motion in a topologically protected fashion, or halted at will, without compromising its adherence to individual lattice sites.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The experimental data that support the findings of this study are available from M.H. upon reasonable request (matthias.heinrich@uni-rostock.de).
Code availability
The MATLAB codes corresponding to the beam-propagation method and band structure algorithms are available from G.G.P. upon reasonable request (pyrialak@knights.ucf.edu).
References
Maczewsky, L. J. et al. Observation of photonic anomalous Floquet topological insulators. Nat. Commun. 8, 13756 (2017).
Mukherjee, S. et al. Experimental observation of anomalous topological edge modes in a slowly driven photonic lattice. Nat. Commun. 8, 13918 (2017).
McIver, J. W. et al. Light-induced anomalous Hall effect in graphene. Nat. Phys. 16, 1058–1063 (2020).
Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).
Aidelsburger, M. et al. Experimental realization of strong effective magnetic fields in an optical lattice. Phys. Rev. Lett. 107, 255301 (2011).
Liu, G., Hao, N., Zhu, S.-L. & Liu, W. M. Topological superfluid transition induced by a periodically driven optical lattice. Phys. Rev. A 86, 013639 (2012).
Nathan, F., Abanin, D., Berg, E., Lindner, N. H. & Rudner, M. S. Anomalous Floquet insulators. Phys. Rev. B 99, 195133 (2019).
Hafezi, M. et al. Imaging topological edge states in silicon photonics. Nat. Photon. 7, 1001–1005 (2013).
Sie, E. J. et al. Valley-selective optical Stark effect in monolayer WS2. Nat. Mater. 14, 290–294 (2015).
Cooper, N. R., Dalibard, J. & Spielman, I. B. Topological bands for ultracold atoms. Rev. Mod. Phys. 91, 015005 (2019).
Wintersperger, K. et al. Realization of an anomalous Floquet topological system with ultracold atoms. Nat. Phys. 16, 1058–1063 (2020).
Peng, Y.-G. et al. Experimental demonstration of anomalous Floquet topological insulator for sound. Nat. Commun. 7, 13368 (2016).
Nathan, F. & Rudner, M. S. Topological singularities and the general classification of Floquet–Bloch systems. New J. Phys. 17, 125014 (2015).
Chiu, C.-K., Teo, J. C. Y., Schnyder, A. P. & Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 88, 035005 (2016).
Roy, R. & Harper, F. Periodic table for Floquet topological insulators. Phys. Rev. B 96, 155118 (2017).
Wang, C., Zhang, P., Chen, X., Yu, J. & Zhai, H. Scheme to measure the topological number of a Chern insulator from quench dynamics. Phys. Rev. Lett. 118, 185701 (2017).
Tarnowski, M. et al. Measuring topology from dynamics by obtaining the Chern number from a linking number. Nat. Commun. 10, 1728 (2019).
Ünal, F. N., Eckardt, A. & Slager, R.-J. Hopf characterization of two-dimensional Floquet topological insulators. Phys. Rev. Res. 1, 022003(R) (2019).
Schuster, T., Gazit, S., Moore, J. E. & Yao, N. Y. Floquet Hopf insulators. Phys. Rev. Lett. 123, 266803 (2019).
Rudner, M. S., Lindner, N. H., Berg, E. & Levin, M. Anomalous edge states and the bulk-edge correspondence for periodically driven two-dimensional systems. Phys. Rev. X 3, 031005 (2013).
Kitagawa, T., Berg, E., Rudner, M. & Demler, E. Topological characterization of periodically driven quantum systems. Phys. Rev. B 82, 235114 (2010).
Nathan, F. & Rudner, M. S. Topological singularities and the general classification of Floquet–Bloch systems. New J. Phys. 17, 125014 (2015).
Carpentier, D. et al. Topological index for periodically driven time-reversal invariant 2D systems. Phys. Rev. Lett. 114, 106806 (2015).
Noh, J. et al. Experimental observation of optical Weyl points and Fermi arc-like surface states. Nat. Phys. 13, 611–617 (2017).
Stützer, S. et al. Photonic topological Anderson insulators. Nature 560, 461–465 (2018).
Lustig, E. et al. Photonic topological insulator in synthetic dimensions. Nature 567, 356–360 (2019).
Maczewsky, L. J. et al. Fermionic time-reversal symmetry in a photonic topological insulator. Nat. Mater. 19, 855–860 (2020).
Bandres, M. A. et al. Topological insulator laser: experiments. Science 359, eaar4005 (2018).
Mukherjee, S. & Rechtsman, M. C. Observation of Floquet solitons in a topological bandgap. Science 368, 856–859 (2020).
Maczewsky, L. J. et al. Nonlinearity-induced photonic topological insulator. Science 370, 701–704 (2020).
Kirsch, M. et al. Nonlinear second-order photonic topological insulators. Nat. Phys. https://doi.org/10.1038/s41567-021-01275-3 (2021).
Pyrialakos, G. et al. Symmetry-controlled edge states in the type-II phase of Dirac photonic lattices. Nat. Commun. 11, 2074 (2020).
Ramachandran, A., Andreanov, A. & Flach, S. Chiral flat bands: existence, engineering, and stability. Phys. Rev. B 96, 161104(R) (2017).
Xia, S. et al. Unconventional flatband line states in photonic Lieb lattices. Phys. Rev. Lett. 121, 263902 (2018).
Goldman, N. & Dalibard, J. Periodically driven quantum systems: effective Hamiltonians and engineered gauge fields. Phys. Rev. X 4, 031027 (2014).
Szameit, A. & Nolte, S. Discrete optics in femtosecond-laser-written photonic structures. J. Phys. B 43, 163001 (2010).
Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014).
Hadad, Y. et al. Self-induced topological protection in nonlinear circuit arrays. Nat. Electron. 1, 178–182 (2018).
Süsstrunk, R. & Huber, S. D. Observation of phononic helical edge states in a mechanical topological insulator. Science 349, 47–50 (2015).
Szameit, A. et al. Quasi-incoherent propagation in waveguide arrays. Appl. Phys. Lett. 90, 241113 (2007).
Acknowledgements
We thank C. Otto for preparing the high-quality fused silica samples used for the inscription of all photonic structures employed in the experiments presented here. G.G.P. acknowledges the support of the Bodossaki Foundation. This work was partially supported by Defense Advanced Research Projects Agency (DARPA; D18AP00058), Office of Naval Research (ONR) Multidisciplinary University Research Initiative (MURI; N00014-16-1-2640, N00014-18-1-2347, N00014-19-1-2052, N00014-20-1-2522, N00014-20-1-2789), Air Force Office of Scientific Research (AFOSR MURI; FA9550-20-1-0322, FA9550-21-1-0202), the National Science Foundation (DMR-1420620, EECS-1711230, ECCS-1454531, DMR-1420620, ECCS-1757025, CBET-1805200, ECCS-2000538, ECCS-2011171), Mathematics and Physical Sciences (MPS) Simons collaboration (Simons grant 733682), W. M. Keck Foundation, US–Israel Binational Science Foundation (BSF 2016381) and the US Air Force Research Laboratory (FA9550-14-1-0037, FA9550-20-1-0322, FA9550-21-1-0202, FA86511820019). We furthermore acknowledge funding from the Deutsche Forschungsgemeinschaft (SCHE 612/6-1, SZ 276/12-1, BL 574/13-1, SZ 276/15-1, SZ 276/20-1) and the Alfried Krupp von Bohlen and Halbach Foundation.
Author information
Authors and Affiliations
Contributions
G.G.P. initiated the idea, formulated the index-modulated lattice and performed the theoretical calculations and simulations. J.B. developed the experimental implementation, fabricated the samples and conducted the measurements. J.B., L.J.M. and M.H. evaluated the measurements and interpreted the data. M.K., N.V.K., A.S. and D.N.C. supervised the efforts of their respective groups. All authors discussed the results and cowrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Materials thanks Alexander Khanikaev, Sunil Mittal and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Comparison of staggered and flat-phased broad excitations.
(a-d): Staggered excitations of the primary waveguides of edge unit cells successfully populate the topological Chern mode near the edge of the Brillouin zone. (e-h) Absent the appropriate phase modulation, the injected wave packets instead represent a superposition of the bulk bands near the center of the Brillouin zone. As a result, the light diffracts freely across the entire lattice instead of being captured in the helical Chern channel.
Extended Data Fig. 2 Honeycomb helical FTI.
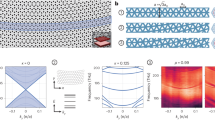
A driven honeycomb lattice with sinusoidally modulated time-periodic coupling terms exhibits a secondary topological phase in response to an increase of the driving period. At the critical driving period \(T_{{{\mathrm{C}}}} = \pi /3\) the gap at the Floquet zone collapses and reopens with a topologically non-trivial winding number. This corresponds to an anomalous phase with a trivial Chern number, signifying a topological phase transition.
Extended Data Fig. 3 Chained honeycomb FTI.
Above its critical modulation period \(T_{{{\mathrm{C}}}}^\prime = \pi\), the chain-driven honeycomb lattice enters a secondary topological phase characterized by the band diagram shown on the right. In this configuration, the bands manifest a non-trivial topological structure characterized by higher order Chern invariants (\({{{\mathcal{C}}}} = 2\)), and, in turn, the Chern gaps host an increased number of unidirectional edge states. Details on the modal amplitudes and propagation dynamics of the Chern states in the \({{{\mathcal{C}}}} = 2\) phase are provided in Supplementary Fig. 5.
Extended Data Fig. 4 Losses in index-modulated waveguides.
Waveguide fluorescence40 characterization confirms that even coarsely discretized index modulation (twelve constant-index segments approximating the ideal cosine Floquet cycle) only introduces excess losses of (0.096 ± 0.010)dB/cm relative to a straight constant-index waveguide. With half of the lattice sites being modulated, the mean excess losses of the bimorphic FTI are (0.048 ± 0.005)dB/cm, substantially below the value of 1.7 dB/cm reported for bending losses in conventional FTIs based on helically modulated waveguides4. Note that the apparent oscillations in the normalized intensity of the modulated waveguide are due to the different concentration of color centers formed at different writing speeds, resulting in a modulation of the fluorescence efficiency between the individual segments of each modulation period. Due to the large number of periods, this oscillation does not notably impact the measurement of the loss coefficient γ. The fluorescence itself is a feature of femtosecond laser-written waveguides in fused silica, and does not pose a substantial source of propagation losses40.
Supplementary information
Supplementary Information
Supplementary Figs. 1–6 and Discussion.
Supplementary Video 1
Simulation of propagation dynamics of two isolated compact localized states in a ribbon lattice. Power is injected into the sites indicated by labels A and B. At the 00:06 time mark, the Floquet modulation is switched off in the vicinity of wave packet B (shaded region). As a consequence, wave packet B couples to a static compact localized state and remains stationary, while wave packet A finds a route around the shaded region. At the 00:20 time mark, the Floquet modulation is restored in the entire lattice, and both wave packets resume propagation to, finally, become spatially interchanged.
Rights and permissions
About this article
Cite this article
Pyrialakos, G.G., Beck, J., Heinrich, M. et al. Bimorphic Floquet topological insulators. Nat. Mater. 21, 634–639 (2022). https://doi.org/10.1038/s41563-022-01238-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-022-01238-w
This article is cited by
-
Hybrid topological photonic crystals
Nature Communications (2023)
-
Observation of nonlinear disclination states
Light: Science & Applications (2023)
-
Floquet metamaterials
eLight (2022)
-
Thermal control of the topological edge flow in nonlinear photonic lattices
Nature Communications (2022)
-
More nodes bring more Floquet modes
Nature Materials (2022)