Abstract
(Ba,K)BiO3 constitute an interesting class of superconductors, where the remarkably high superconducting transition temperature Tc of 30 K arises in proximity to charge density wave order. However, the precise mechanism behind these phases remains unclear. Here, enabled by high-pressure synthesis, we report superconductivity in (Ba,K)SbO3 with a positive oxygen–metal charge transfer energy in contrast to (Ba,K)BiO3. The parent compound BaSbO3−δ shows a larger charge density wave gap compared to BaBiO3. As the charge density wave order is suppressed via potassium substitution up to 65%, superconductivity emerges, rising up to Tc = 15 K. This value is lower than the maximum Tc of (Ba,K)BiO3, but higher by more than a factor of two at comparable potassium concentrations. The discovery of an enhanced charge density wave gap and superconductivity in (Ba,K)SbO3 indicates that strong oxygen–metal covalency may be more essential than the sign of the charge transfer energy in the main-group perovskite superconductors.
Similar content being viewed by others
Main
Superconducting bismuthates, BaPb1–xBixO3 (BPBO)1 and Ba1–xKxBiO3 (BKBO)2,3, have attracted considerable research interest since their discovery more than three decades ago. The parent compound BaBiO3 (BBO) is known to be a non-magnetic, commensurate charge density wave (CDW) insulator. The CDW order is accompanied by a breathing octahedral distortion; that is, two octahedra with different sizes order in a three-dimensional chequerboard pattern4,5. As the CDW order is suppressed via chemical substitution of Bi with Pb or Ba with K (refs. 6,7), the compounds become superconducting up to a maximum Tc of 12 K in BPBO, and 30 K in BKBO. Numerous experiments have established that the mechanism of superconductivity is largely conventional; the pairing symmetry is s-wave8, and the oxygen isotope effect is consistent with the Bardeen–Cooper–Schrieffer (BCS) theory9, meaning electron–phonon interaction plays the important role in superconductivity. Nevertheless, the unexpectedly high Tc of BKBO, despite a rather low carrier density, has triggered various critical questions as to the driving mechanism and the correct model of the CDW order and superconductivity in these materials. For example, recent studies suggest that the additional consideration of long-range exchange interactions and many-body effects can be crucial for the quantitative description of the CDW gap10,11 as well as for superconductivity12,13,14.
Superconducting bismuthates have long been considered as archetypal candidates for unconventional superconductors in which an effective electron–electron interaction U is negative 15,16, leading to electron pairing in real as well as in momentum spaces17,18. The real-space pairing occurs in the parent compound BBO, which is argued to be a typical valence-skipping compound with unstable tetravalent bismuth (6s1) disproportionated into tri- (6s2) and pentavalent (6s0). As the charge disproportionation on the bismuth sites is suppressed via chemical doping and the bismuth valence starts to dynamically fluctuate, negative U, which causes pairing of two electrons in the Bi3+–O6 octahedra, could also pair them in k-space. The negative U model may provide a possible framework to understand superconductivity in the bismuthates as well as some chalcogenides19 with valence-skipping elements.
While the negative U model emphasizes the role of bismuth, an alternative model asserts the role of oxygen and its hybridization with bismuth6,20,21,22. This model’s foundation is that the charge transfer energy ΔCT of the bismuthates is negative, as the on-site energy of the Bi 6s orbital is lower than that of the oxygen 2p, owing to the large scalar relativistic effect of heavy bismuth23. Consequently, electronic states around the Fermi level (which originate from the strongly hybridized spσ* states) show predominantly oxygen 2p character. This crucially modifies the preceding understanding of the CDW order in BBO; it should be described not by the charge disproportionation (6s2 + 6s0) but rather by the bond-length disproportionation as 6s2 + 6s2L2, where L denotes a ligand hole. Spectroscopic evidence supports the oxygen-hole model24,25,26. As the CDW order is suppressed, oxygen holes become delocalized, giving rise to superconductivity, possibly via strong electron–phonon coupling21,27. The importance of oxygen holes has previously been demonstrated in the Zhang–Rice model28 for cuprates, in which holes on the copper and oxygen sites form a strongly hybridized singlet state, highlighting their potential role in understanding the CDW order and high-Tc superconductivity in the bismuthates as well.
In spite of their scientific importance, a contrastive analysis of the effects of bismuth and oxygen has so far been limited due to lack of compounds analogous to the bismuthates. Perovskite antimonates are ideal candidates to study; antimony is isovalent to bismuth. Higher on-site energy of the Sb 5s orbital compared to the Bi 6s may enable us to tune the ΔCT of the material from negative to almost zero or even positive; therefore the states around the Fermi level are expected to show stronger metal s character. First-principles calculations of a hypothetical primitive cubic perovskite BaSbO3 (BSO) have been previously conducted and compared with those of BBO29,30,31. The results clearly indicate that the Sb 5s level is well above the Bi 6s level, increasing ΔCT from established negative values in BBO to higher energy values in BSO. It would therefore be enlightening to see the impact of this drastic change of ΔCT on both superconductivity and CDW in antimonates, which should give us a hint to identify the key ingredient of high-Tc superconductivity in BKBO.
Several attempts have been made to synthesize superconducting antimonates, but with limited success. It was reported that partially doped BaPb0.75Sb0.25O3 becomes superconducting32, but its Tc is substantially decreased compared to that of BPBO. However, superconducting perovskite antimonates, with only antimony occupying the octahedral sites of perovskites, have yet to be experimentally reported, to the best of our knowledge. This is probably because the strongly covalent Sb–O bond is known to hamper forming 180 degree Sb–O–Sb bonds33, and as a consequence, no perovskite antimonates have been realized to date except a highly distorted insulating NaSbO3 (ref. 34). Here, we report superconducting antimonates Ba1−xKxSbO3 (BKSO), which we were able to stabilize via high-pressure high-temperature synthesis routes, enabling clarification of possible driving mechanisms for CDW and superconductivity in the compounds by comparing their properties with the sibling compound, BKBO.
To shed light on the effects that varying ΔCT has on the electronic structure, the band structures of BKSO as well as BKBO are calculated via a hybrid density functional theory (DFT) method10, as shown in Fig. 1 (total and projected density of states (DOS) are in Extended Data Fig. 1). The calculations are conducted for primitive cubic structures without the breathing distortions, which were experimentally obtained at the potassium concentration x = 0.65. The band structure of BKBO in Fig. 1b comprises the spσ* band around the Fermi level and the spσ band below –7 eV, which lie above and below the non-bonding flat O 2pπ bands (around –2 and –4 eV), respectively. The band structure of BKSO in Fig. 1d shares these common overall features, but the locations of the O 2pπ bands are pushed down appreciably, demonstrating the elevated Sb 5s orbital energy relative to the Bi 6s, as pointed out previously29,30,31. In Fig. 1b,d, the sum of the O 2pσ and Bi-6s/Sb-5s contributions and their composition are indicated by the thickness and colour; blue denotes predominant O 2pσ character and red denotes predominant Bi-6s/Sb-5s character (the O 2pπ contribution is in Extended Data Fig. 2). The analysis of the orbital composition indeed demonstrates that ΔCT for BKSO is almost zero and slightly positive, in contrast to BKBO with negative ΔCT, as schematically shown in Fig. 1a. In BKBO, the red region with predominant Bi 6s character can be identified at the Γ point. Its energy, E = − 5.4 eV, is a good measure of the Bi 6s orbital energy, as the Bi 6s state does not hybridize with O 2p states at Γ in the cubic symmetry31,34,35. Clearly, the energy of the Bi 6s state is below the average energy of the flat O 2pπ bands, E = –2.9 eV (Extended Data Fig. 2 and Supplementary Table 1). By sharp contrast, the location of the red region at the Γ point in BKSO, a measure of the Sb 5s orbital energy, is at E = –4.0 eV, which is only slightly above the average energy of the O 2pπ bands, E = –4.8 eV. The clear contrast of predominant orbital character between the lower spσ and higher spσ* bands, the Bi 6s (red) and O 2pσ (blue) characters, respectively, is evident for BKBO in Fig. 1b, indicating that the orbital energy of O 2pσ is higher than that of Bi 6s, namely, ΔCT < 0. In BKSO (Fig. 1d), the red/blue contrast is reversed, with more O 2pσ character (blue) in the spσ band and more Sb 5s character (red) in the spσ* band, meaning ΔCT ≥ 0. The more covalent character of BKSO, closer to the covalent limit ΔCT = 0 compared to BKBO, can be seen as the strongly reduced contrast between the spσ and spσ* bands in the ratio of Sb 5s and O 2pσ contributions to the DOS in Extended Data Fig. 1. We note that the previous estimates of ΔCT in a hypothetical BSO based on a tight-binding fitting gave the sign of ΔCT as either positive29 or negative31, depending on the model used. Incidentally, a fitting of the present band calculation based on Wannierization (Supplementary Fig. 1 and Supplementary Table 2) gives a positive value. The estimates of ΔCT are quite useful in visualizing material trends within the same model, but are subject to model-dependent uncertainties in quantitative comparison across different models, as each model uses limited and different varied orbital bases and hopping terms to obtain ‘effective’ orbital energies and transfers. Here, we rely only on the qualitative arguments based on the orbital composition of the band structure to position BKSO in Fig. 1a.
a, A schematic diagram of different regimes of metallicity in BKBO and BKSO. When charge transfer energy ΔCT is positive (negative), Bi or Sb s electrons (oxygen holes) are predominant. b, The fat-band representation of the electronic band structure of BKBO at x = 0.65 calculated via hybrid DFT. The thickness is proportional to the sum of O 2pσ and Bi 6s contributions, and the colours represent their ratio, with predominant O 2pσ character shown by blue and predominant Bi 6s character by red. The plot shows the predominant O 2pσ (Bi 6s) character in the spσ* (spσ) band. A band with predominant Bi 6s character at Γ at −5.4 eV is formed by non-bonding Bi 6s states (Extended Data Fig. 2 for the O 2pπ contribution). EF, Fermi energy. c, The molecular-orbital diagram of BKBO derived from b. The Bi 6s orbital energy is markedly lower than the O 2p energy, consistent with negative ΔCT. Therefore, BKBO is located in the scheme of the oxygen-hole metal20,21, as illustrated in a. d, The fat-band representation of the electronic band structure of BKSO at x = 0.65 calculated via hybrid DFT. Sb 5s and oxygen 2p are found to be highly mixed in both spσ and spσ* bands. The much enhanced Sb 5s character in the spσ* band is clear compared to that of Bi 6s in BKBO. The non-bonding Sb 5s states at Γ are at −4.0 eV (Extended Data Fig. 2 for the O 2pπ contribution). e, The molecular-orbital diagram for BKSO derived from d. The Sb 5s orbital energy is marginally higher than the O 2p energy, indicating that ΔCT is slightly positive while being close to zero (ΔCT ≳ 0). Thus, BKSO is located in the region of the Bi/Sb s-orbital metal while critically close to the covalency limit in a.
Having clarified the inverted ΔCT of BKSO as compared to that of BKBO, we next reveal how the inversion modifies physical properties of the materials. Polycrystalline samples of BKSO with potassium content x from 0 to 0.75 were synthesized under a high-pressure, high-temperature condition of 12 GPa and 1,300 °C (Methods for details of sample synthesis and characterization). The parent compound BaSbO3−δ is found to be a robust insulator with a large CDW gap. Rietveld refinement of neutron powder diffraction data (Supplementary Fig. 2a) confirms face-centred cubic symmetry (space group Fm\(\bar 3\)m) with the breathing distortion, and furthermore reveals two distinct Sb–O bond lengths, 2.24(1) and 2.01(1) Å (Fig. 2a). Surprisingly, the difference between the two bond lengths Δd = 0.23 Å is larger than that of BBO (Δd = 2.28 − 2.11 = 0.16 Å, Fig. 2b)4. The observation of the breathing distortion establishes the commensurate CDW order from the structural point of view, which results in a bandgap in the material. Using diffusive reflectance spectroscopy, the bandgap in BSO is determined to be 2.54 eV (Fig. 2c). The value is appreciably larger than that in BBO (2.02 eV)36, consistent with the larger bond-length disproportionation observed in the neutron diffraction.
a,b, Schematic diagrams of expanded and contracted octahedra in BaSbO3−δ (a) and BBO (b). d denotes bond length between metal and oxygen ions. From the neutron diffraction investigations (Supplementary Fig. 2), two distinct Sb–O bond lengths are estimated to be 2.24(1) and 2.01(1) Å, respectively (Supplementary Table 3 for detailed structural parameters). The difference between the two bond lengths is found to be larger than that of BBO (ref. 4). c, Optical absorbance of BaSbO3−δ at 300 K shows a wide bandgap ECDW of 2.54 eV caused by the formation of the CDW order. By comparison, the optical conductivity (σ1) of BBO (ref. 50) is plotted as a reference, indicating the CDW gap of BaSbO3−δ is larger than that of BBO.
The CDW order of the antimonate can be suppressed by substituting Ba with K up to 65%. X-ray and neutron powder diffraction measurements enable us to map out the structural phase diagram of BKSO, as shown in Fig. 3a (detailed refinement profiles and refined parameters are in Supplementary Figs. 2 and 3 and Supplementary Table 3). As x increases, two structural transitions are found, namely, from Fm\(\bar 3\)m to a tetragonal I4/mcm at x ≈ 0.3, and from I4/mcm to a primitive cubic Pm\(\bar 3\)m phase at x ≈ 0.65. This structural phase diagram is qualitatively similar to that of BKBO37, in which the CDW order is sequentially suppressed from the long range (I2/m) to short range (Ibmm) and then finally disappears (Pm\(\bar 3\)m). The structural transitions trigger drastic successive changes in Raman scattering, as shown in Fig. 3b. The undoped compound shows a pronounced peak at 672 cm−1, which corresponds to the breathing-mode phonon, that is, the symmetric movement of oxygen ions with A1g symmetry, and is also known to be crucial to superconductivity in BKBO38. The phonon peak is first marginally softened as x increases, and next its amplitude completely vanishes for x ≥ 0.65. Because all the phonon modes become Raman-inactive in the Pm\(\bar 3\)m phase39, the vanishing breathing-mode peak confirms that the crystal symmetry above x = 0.65 is indeed Pm\(\bar 3\)m with the ideal cubic perovskite structure without any distortion; that is, the CDW order is completely suppressed. Interestingly, the critical potassium concentration xIMT at which the structure symmetry becomes Pm\(\bar 3\)m is larger in BKSO (xIMT ≈ 0.65) than in BKBO (xIMT ≈ 0.35). The larger xIMT is plausibly related to the bigger CDW gap, which may necessitate more holes for its suppression in the antimonates.
a, The structural phase diagram of BKSO based on neutron (Supplementary Fig. 2) and X-ray (Supplementary Fig. 3) diffraction data. Black diamonds, tan crosses and red squares represent the face-centred cubic (fcc, Fm\(\bar 3\)m), tetragonal (T, I4/mcm) and primitive cubic (C, Pm\(\bar 3\)m) phases, respectively. The insets depict the local atomic structure of each phase, which shows transitions of the CDW order from the commensurate long range (Fm\(\bar 3\)m) to short range (I4/mcm), and finally to complete suppression (Pm\(\bar 3\)m). b, Raman spectra of BKSO measured with the excitation wavelength of 632 nm at 300 K. ω denotes the Raman shift in the unit of wavenumber. As highlighted in the dashed box, the breathing-mode phonon peak observed in the Fm\(\bar 3\)m and I4/mcm phases disappears in the Pm\(\bar 3\)m phase (x ≥ 0.65), confirming the CDW order is completely suppressed. The inset shows a schematic picture of the breathing-mode phonon.
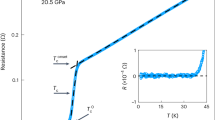
The BKSO samples with x ≧ 0.65 and Pm\(\bar 3\)m symmetry shows bulk superconductivity with a maximum Tc = 15 K at x = 0.65 (Fig. 4). The superconducting transition of the optimally doped sample (x = 0.65) is clearly identified at Tc = 15 K in resistivity (Fig. 4a). In the magnetic susceptibility (Fig. 4b), a diamagnetic signal corresponding to a superconducting volume fraction near 100% is observed below Tc = 15 K. The specific heat shows a jump with an onset at 15 K due to the superconducting transition, which is suppressed by applying a magnetic field of 1 T (Fig. 4c). The magnitude of the jump is on the order of the linear specific heat coefficient γ (0.924 mJ mol−1 K−2; Supplementary Fig. 4), confirming the bulk nature of superconductivity. The maximum Tc = 15 K of BKSO at x = 0.65 is found to be lower than that of BKBO at x = 0.4, Tc ≈ 30 K, but at comparable potassium concentrations, is higher than that of BKBO (7.0 K at x = 0.66 (ref. 40)) by more than a factor of two, as seen in Fig. 4b.
a, Superconducting transition observed in the resistivity (ρ) of optimally doped antimonate (x = 0.65). T denotes temperature. The superconducting transition temperature Tc, defined by the clear onset of the transition, is ~15 K. b, The superconducting transition of the same sample is observed in zero-field-cooled magnetic susceptibility (χ) measured at μ0H = 0.001 T (red), in comparison with that of Ba0.34K0.66BiO3 (grey)40. H is an applied magnetic field, and μ0 is the vacuum permeability. The diamagnetic volume fraction is near 100%, indicating bulk superconductivity. Here, Tc is 15 K, defined as a temperature where the volume fraction started increasing by 0.1%. c, The superconducting transition of the same sample observed in the specific heat. ΔC denotes the difference between specific heats (C) under each field and 14 T. Tc is estimated to 15 K from the clear onset of jump, which can be suppressed by applying a field of 1 T. The observed jump is broadened, perhaps indicating sample inhomogeneity from the high-pressure synthesis. d, Oxygen K-edge X-ray absorption spectrum of Ba0.35K0.65SbO3 (red open circles) at 300 K, plotted together with that of Ba0.4K0.6BiO3 (ref. 41; grey open triangles). The intensity of each spectrum is normalized by that at a high energy ~550 eV above the edge. The arrows indicate the prepeak structure originating from oxygen 2p holes in the spσ* band. The suppression of the prepeak intensity in the antimonate indicates the decrease of oxygen holes compared to the bismuthate.
Reduced oxygen-hole character in BKSO is revealed via X-ray absorption spectroscopy, consistent with its positive ΔCT. The oxygen K-edge, which probes unoccupied oxygen 2p states, is measured for the optimally doped BKSO and compared with a BKBO reference41 at similar x in Fig. 4d. The BKBO (x = 0.6) exhibits a pronounced prepeak structure at E = 528.8 eV, indicating predominant oxygen holes in the conduction band. The BKSO (x = 0.65) sample shows a similar prepeak at the same energy, but its intensity is appreciably diminished, indicating the reduction of the oxygen-hole density. The suppression of the prepeak intensity in BKSO compared with BKBO41,42 is observed not only around x = 0.65, but also in all the available x range including x = 0 (BSO; Extended Data Fig. 3). We also note that a clear signature of charge disproportionation of Sb3+ and Sb5+ has been observed very recently in 121Sb Mössbauer spectroscopy in BSO43. No such clear spectroscopic signature of Bi3+ and Bi5+ has been reported in BBO which can be attributed to the predominant oxygen holes24,25,26. The stark contrast between BKSO and BKBO supports the strong metal s character and the reduced O 2p character of the spσ* band and hence the positive sign of ΔCT in BKSO.
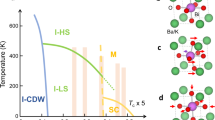
A phase diagram of BKSO, compiled from these results, offers a comprehensive view of the interplay between the CDW order and superconductivity in main-group oxide superconductors (Fig. 5). First, a common tendency in the phase diagram can be found in both compounds; as the CDW insulating phase is suppressed, a half-dome of superconductivity arises with Tc maximized at the border of the insulator-to-metal transition and gradually decreasing with x increasing. Nevertheless, a crucial difference between the two compounds is that the suppression of the CDW phase occurs at higher x in BKSO, possibly related to its larger CDW gap. As BKSO shows a higher Tc at x ≥ 0.65, its Tc could exceed that of BKBO if it were possible to stabilize metallic BKSO at lower x and if the same trend of Tc based on x held. In reality, this has so far been prohibited by the strong CDW instability in BKSO, setting a limit on enhancing the superconductivity further.
Red circles are the Tc values of superconductivity (SC) in the antimonates with the same definition as in Fig. 4, and grey triangles are Tc of BKBO (refs. 40,51). Tc values of the antimonates show a half-dome shape (red region), which is similar to that of the bismuthates (dark grey). The crucial difference is that the CDW order in the bismuthates (light grey region) is suppressed at x = 0.4, whereas that of the antimonates (green region) continues to exist up to x = 0.65.
The superconducting Tc that is more than doubled in BKSO at x = 0.65 suggests a mechanism associated with strong metal–oxygen covalency. The electronic structure in Fig. 1e and Extended Data Fig. 1 points to the close proximity of the orbital energies of Sb 5s and O 2p, ΔCT ≈ 0, indicating the strong covalency in BKSO. This leads to the Sb–O bonds being stiffer than the Bi–O bonds, and the relevant phonon energies of BKSO being higher than those of BKBO, as supported by the following experiments. First, the Debye temperature of the optimally doped BKSO was found to be 535 K (Supplementary Fig. 4), which is greater than that of BKBO, typically ~330 K (ref. 44). Second, the breathing-mode phonon in the parent compounds showed its frequency increased by about 19% in BSO (672 cm−1), as compared to BBO39 (565 cm−1; Supplementary Fig. 5). The increase of the phonon frequencies can be a factor in increasing Tc but alone cannot fully account for the more than twofold enhancement of Tc in BKSO at x = 0.65 in terms of the Macmillan’s formula for superconducting Tc. This implies that the increase of the electron–phonon coupling, possibly linked with the enhanced covalency, must be incorporated in the enhancement of superconductivity as well (Supplementary Note 1 for more detailed discussion). The stronger CDW instability in BKSO could also be related to such an enhanced electron–phonon coupling, which is reminiscent of covalent superconductors in which too large electron–phonon coupling sometimes leads to lattice instability instead of higher Tc (refs. 45,46).
Finally, yet importantly, our study affords insight into the role of negative ΔCT and predominant oxygen holes. On one hand, it is evident from the results that BKSO, which has slightly positive ΔCT, demonstrates both CDW insulating and superconducting phases, analogous to BKBO. Therefore, the emergence of the two phases is not necessarily dependent on the sign of ΔCT. In addition, at x ≥ 0.65, BKSO shows even higher Tc than BKBO, in spite of its decreased oxygen-hole character. Hence, it could be inferred that predominant oxygen holes may not be a necessary condition for enhancement of superconductivity. On the other hand, BKBO, which has more oxygen holes, shows a smaller amplitude of the CDW order than that in BKSO, which results in a smaller xIMT as well. Since the electronic DOS at the Fermi level as well as the electron–phonon interaction become larger with decreasing x (ref. 14), a smaller xIMT would lead to an increased Tc. Therefore, the weakened CDW order in BKBO, likely by predominant oxygen holes, could be vital to show a higher Tc. In this respect, predominant oxygen holes may be a sufficient condition for a higher Tc.
We have reported superconducting perovskite antimonates with a maximum Tc of 15 K. The modification of ΔCT via the substitution of Bi with Sb has allowed us to address long-standing questions as to the different roles of metal and oxygen ions for the CDW and superconductivity in the main-group oxide superconductors. Furthermore, these results provide fascinating possibilities for approaching novel regimes in the future. For example, it would be intriguing to modify ΔCT either to be more positive or negative by utilizing appropriate elements at the octahedral site: As and Sn would give an on-site energy of a metal s level higher than Sb, and thus more positive ΔCT value than antimonates. Assuming these compounds can be stabilized, they would show more prominent effects of the cations, providing ideal model systems to examine the negative U model and the effects of valence fluctuations18. On the other hand, Te (ref. 47) and I (ref. 48) would give an on-site energy of a metal s level lower than Sb, and perhaps comparable or even lower than Bi. Thus, their ΔCT values would be more negative than those of the antimonates and possibly bismuthates, providing additional model systems to comprehensively examine the effect of oxygen holes20. We also note that charge- or bond-disproportionated CDW states are not limited to oxides but extend to other families, including perovskite halides CsTlCl3 or CsTlF3 (ref. 49).
Methods
Sample synthesis and characterization
Polycrystalline samples of BKSO (x = 0.0, 0.36, 0.50, 0.65 and 0.75) were fabricated using a high-pressure high-temperature synthesis technique with a Walker-type multi-anvil module. Precursors of BaO2 (95%, Acros Organics), KO2 (96.5%, Alfa Aesar), Sb (99.999%, ChemPur) and Sb2O3 (99.999%, Aldrich) were mixed in stoichiometric ratios and transferred into a Pt capsule. The samples were obtained from high-pressure high-temperature treatment at 12 GPa and 1,300 °C for an hour, followed by quenching to room temperature and slow decompression. A dense pellet of the samples was recovered from the Pt capsule, after which its outer face was polished using a diamond file. Powder X-ray and neutron diffraction data were collected in the Debye–Scherrer geometry using a Mo Kα1 source and a time-of-flight neutron source, respectively, with the instrument WISH at ISIS. The structural refinements based on neutron and X-ray diffraction patterns, shown in Supplementary Figs. 2 and 3, indicate that the samples consist of an almost pure BKSO perovskite phase with only a very minor trace of BaSbO2.5 for x = 0 and KSbO3 for x ≠ 0 as the impurity phases. The X-ray refinements reveal no clear signature of cation non-stoichiometry and the K contents, x, are in good agreement with the nominal values for all the samples. The neutron refinement suggests an oxygen deficiency on the order of a few percent only for BaSbO3−δ (x = 0). The oxygen deficiency in BaSbO3−δ is not large as compared with its sibling compound BaBiO3−δ, which is known to be easily reduced at relatively low temperatures and oxygen partial pressures52.
Physical property measurements
Magnetic susceptibility was measured via a Quantum Design magnetic property measurement system, and resistivity and heat capacity were measured via a Quantum Design physical property measurement system. Optical absorbance was measured via diffuse reflectance spectroscopy at room temperature. X-ray absorption spectroscopy was measured in partial fluorescence yield mode using a silicon drift detector to select the O K-edge fluorescence at the Spherical Grating Monochromator beamline and in total fluorescence yield mode using a microchannel plate at the Resonant Elastic and Inelastic X-ray Scattering beamline of the Canadian Light Source.
First-principles calculation
The band structures of BKSO and BKBO were calculated using the WIEN2k code53 with full hybrid functionals (YS-PBE0, similar to HSE06 (ref. 54)). We found that a 12 × 12 × 12 reciprocal-space k mesh is sufficient for the calculations well converged. RMTKMAX was set to 7.0, where RMT is the smallest atomic sphere radius and KMAX is the maximal k in the plane wave expansion. The virtual crystal approximation was used to take into account the solid solution of Ba and K ions. The atomic structures reported from experiments were used.
Data availability
The data that support the findings of this work are available from the corresponding authors upon reasonable request.
References
Sleight, A. W., Gillson, J. L. & Bierstedt, P. E. High-temperature superconductivity in BaPb1-xBixO3 system. Solid State Commun. 17, 27–28 (1975).
Mattheiss, L. F., Gyorgy, E. M. & Johnson, D. W. Superconductivity above 20 K in the Ba-K-Bi-O system. Phys. Rev. B 37, 3745–3746 (1988).
Cava, R. J. et al. Superconductivity near 30 K without copper: the Ba0.6K0.4BiO3 perovskite. Nature 332, 814–816 (1988).
Cox, D. E. & Sleight, A. W. Crystal structure of Ba2Bi3+Bi5+O6. Solid State Commun. 19, 969–973 (1976).
Thonhauser, T. & Rabe, K. M. Fcc breathing instability in BaBiO3 from first principles. Phys. Rev. B 73, 212106 (2006).
Mattheiss, L. F. & Hamann, D. R. Electronic structure of BaPb1–xBixO3. Phys. Rev. B 28, 4227–4241 (1983).
Mattheiss, L. F. & Hamann, D. R. Electronic structure of the high-Tc superconductor Ba1–xKxBiO3. Phys. Rev. Lett. 60, 2681–2684 (1988).
Huang, Q. et al. Tunneling evidence for predominantly electron phonon coupling in superconducting Ba1–xKxBiO3 and Nd2–xCexCuO4–y. Nature 347, 369–372 (1990).
Hinks, D. G., Richards, D. R., Dabrowski, B., Marx, D. T. & Mitchell, A. W. The oxygen isotope effect in Ba0.625K0.375BiO3. Nature 335, 419–421 (1988).
Franchini, C., Kresse, G. & Podloucky, R. Polaronic hole trapping in doped BaBiO3. Phys. Rev. Lett. 102, 256402 (2009).
Nourafkan, R., Marsiglio, F. & Kotliar, G. Model of the electron-phonon interaction and optical conductivity of Ba1–xKxBiO3 superconductors. Phys. Rev. Lett. 109, 017001 (2012).
Yin, Z. P., Kutepov, A. & Kotliar, G. Correlation-enhanced electron-phonon coupling: applications of GW and screened hybrid functional to bismuthates, chloronitrides, and other high-Tc superconductors. Phys. Rev. X 3, 021011 (2013).
Wen, C. H. P. et al. Unveiling the superconducting mechanism of Ba0.51K0.49BiO3. Phys. Rev. Lett. 121, 117002 (2018).
Li, Z. L., Antonius, G., Wu, M., da Jornada, F. H. & Louie, S. G. Electron-phonon coupling from ab initio linear-response theory within the GW method: correlation-enhanced interactions and superconductivity in Ba1–xKxBiO3. Phys. Rev. Lett. 122, 186402 (2019).
Anderson, P. W. Model for the electronic structure of amorphous semiconductors. Phys. Rev. Lett. 34, 953–955 (1975).
Emery, V. J. Theory of the quasi-one-dimensional electron gas with strong “on-site” interactions. Phys. Rev. B 14, 2989–2994 (1976).
Rice, T. M. & Sneddon, L. Real-space and k-space electron pairing in BaPb1–xBixO3. Phys. Rev. Lett. 47, 689–692 (1981).
Varma, C. M. Missing valence states, diamagnetic insulators, and superconductors. Phys. Rev. Lett. 61, 2713–2716 (1988).
Matsushita, Y., Bluhm, H., Geballe, T. H. & Fisher, I. R. Evidence for charge Kondo effect in superconducting Tl-doped PbTe. Phys. Rev. Lett. 94, 157002 (2005).
Foyevtsova, K., Khazraie, A., Elfimov, I. & Sawatzky, G. A. Hybridization effects and bond disproportionation in the bismuth perovskites. Phys. Rev. B 91, 121114 (2015).
Khazraie, A., Foyevtsova, K., Elfimov, I. & Sawatzky, G. A. Oxygen holes and hybridization in the bismuthates. Phys. Rev. B 97, 075103 (2018).
Ignatov, A. Y. Relationship between the electronic and local structure in BaPbxBi1–xO3 and Ba1–xKxBiO3 perovskites. Nucl. Instrum. Methods Phys. Res. A 448, 332–339 (2000).
Pyykko, P. Relativistic effects in structural chemistry. Chem. Rev. 88, 563–594 (1988).
Wertheim, G. K., Remeika, J. P. & Buchanan, D. N. E. Electronic structure of BaPb1–xBixO3. Phys. Rev. B 26, 2120–2123 (1982).
Shen, Z. X. et al. Photoemission study of monoclinic BaBiO3. Phys. Rev. B 40, 6912–6918 (1989).
Plumb, N. C. et al. Momentum-resolved electronic structure of the high-Tc superconductor parent compound BaBiO3. Phys. Rev. Lett. 117, 037002 (2016).
Hirsch, J. E. & Marsiglio, F. Superconducting state in an oxygen hole metal. Phys. Rev. B 39, 11515–11525 (1989).
Zhang, F. C. & Rice, T. M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 37, 3759–3761 (1988).
Julien, J. P., Papaconstantopoulos, D. A., Cyrotlackmann, F. & Pasturel, A. Calculations of the electronic structure and superconducting properties of BaPb1–xSbxO3. Phys. Rev. B 43, 2903–2909 (1991).
Singh, D. J., Papaconstantopoulos, D. A., Julien, J. P. & Cyrotlackmann, F. Electronic structure of Ba(Sn,Sb)O3: absence of superconductivity. Phys. Rev. B 44, 9519–9523 (1991).
Benam, M. R., Foyevtsova, K., Khazraie, A., Elfimov, I. & Sawatzky, G. A. Bond versus charge disproportionation and nature of the holes in s−p ABX3 perovskites. Phys. Rev. B 104, 195141 (2021).
Cava, R. J. et al. Superconductivity at 3.5 K in BaPb0.75Sb0.25O3: why is Tc so low? Nature 339, 291–293 (1989).
Goodenough, J. B. & Kafalas, J. A. Exploring A+B5+O3 compounds. J. Solid State Chem. 6, 493–501 (1973).
Mizoguchi, H., Woodward, P. M., Byeon, S. H. & Parise, J. B. Polymorphism in NaSbO3: structure and bonding in metal oxides. J. Am. Chem. Soc. 126, 3175–3184 (2004).
Hughbanks, T. Superdegenerate electronic energy levels in extended structures. J. Am. Chem. Soc. 107, 6851–6859 (1985).
Sato, H., Tajima, S., Takagi, H. & Uchida, S. Optical study of the metal-insulator transition on Ba1–xKxBiO3 thin-films. Nature 338, 241–243 (1989).
Pei, S. Y. et al. Structural phase diagram of the Ba1–xKxBiO3 system. Phys. Rev. B 41, 4126–4141 (1990).
Loong, C. K. et al. High-energy oxygen phonon modes and superconductivity in Ba1–xKxBiO3: an inelastic-neutron-scattering experiment and molecular-dynamics simulation. Phys. Rev. Lett. 62, 2628–2631 (1989).
Tajima, S., Yoshida, M., Koshizuka, N., Sato, H. & Uchida, S. Raman-scattering study of the metal-insulator transition in Ba1–xKxBiO3. Phys. Rev. B 46, 1232–1235 (1992).
Kim, D. C. et al. High pressure synthesis and superconductivity of Ba1–xKxBiO3 (0.35 < x < 1). Physica C 383, 343–353 (2003).
Kobayashi, K. et al. Doping dependence of the electronic structure of Ba1–xKxBiO3 studied by X-ray-absorption spectroscopy. Phys. Rev. B 59, 15100–15106 (1999).
Balandeh, S. et al. Experimental and theoretical study of the electronic structure of single-crystal BaBiO3. Phys. Rev. B 96, 165127 (2017).
Kim, M. et al. Mixed valence and superconductivity in perovskite antimonates. Chem. Mater. 33, 6787–6793 (2021).
Woodfield, B. F., Wright, D. A., Fisher, R. A., Phillips, N. E. & Tang, H. Y. Superconducting-normal phase transition in (Ba1–xKx)BiO3, x = 0.40, 0.47. Phys. Rev. Lett. 83, 4622–4625 (1999).
Moussa, J. E. & Cohen, M. L. Two bounds on the maximum phonon-mediated superconducting transition temperature. Phys. Rev. B 74, 094520 (2006).
Esterlis, I., Kivelson, S. A. & Scalapino, D. J. A bound on the superconducting transition temperature. npj Quantum Mater. 3, 59 (2018).
Christy, A. G., Mills, S. J. & Kampf, A. R. A review of the structural architecture of tellurium oxycompounds. Mineral. Mag. 80, 415–545 (2016).
Volonakis, G., Sakai, N., Snaith, H. J. & Giustino, F. Oxide analogs of halide perovskites and the new semiconductor Ba2AglO6. J. Phys. Chem. Lett. 10, 1722–1728 (2019).
Retuerto, M. et al. Synthesis and properties of charge-ordered thallium halide perovskites, CsTl+0.5Tl3+0.5X3 (X = F or Cl): theoretical precursors for superconductivity? Chem. Mater. 25, 4071–4079 (2013).
Kim, G. et al. Suppression of three-dimensional charge density wave ordering via thickness control. Phys. Rev. Lett. 115, 226402 (2015).
Nagata, Y., Mishiro, A., Uchida, T., Ohtsuka, M. & Samata, H. Normal-state transport properties of Ba1–xKxBiO3 crystals. J. Phys. Chem. Solids 60, 1933–1942 (1999).
Sakuma, H., Hashizume, H. & Yamanaka, A. Bi ordering in high-temperature structures of BaBiO3–x. Acta Cryst. B46, 693–698 (1990).
Blaha, P. et al. WIEN2k: an APW+lo program for calculating the properties of solids. J. Chem. Phys. 152, 074101 (2020).
Krukau, A. V., Vydrov, O. A., Izmaylov, A. F. & Scuseria, G. E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125, 224106 (2006).
Merz, M. et al. X-ray absorption of Ba1−xKxBiO3 and BaPb1−yBiyO3: competition between bipolaronic and charge-density wave states. EPL 72, 275–281 (2005).
Garbassi, F. XPS and AES study of antimony oxides. Surf. Interface Anal. 2, 165–169 (1980).
Acknowledgements
We thank P. Adler, K. Foyevtsova, G. Khaliullin, H. Mizoguchi, J.-G. Park and J. Yu for discussions, and U. Engelhardt, F. Falkenberg, W. Kain, K. Schunke and S. Strobel for experimental support. This research was carried out in part due to funding from the Max Planck-UBC-UTokyo Centre for Quantum Materials. Part of the research described in this paper was performed at the Canadian Light Source, a national research facility of the University of Saskatchewan, which is supported by the Canada Foundation for Innovation, the Natural Sciences and Engineering Research Council, the National Research Council, the Canadian Institutes of Health Research, the Government of Saskatchewan and the University of Saskatchewan. We thank the Science and Technology Facilities Council ISIS facility for the provision of beamtime.
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
M.K. and H.T. conceived the project. M.K. prepared and characterized the samples. T.T., M.I. and R.K.K. helped with the analysis. M.K., G.M.M., A.S.G. and P.M. conducted the neutron diffraction experiments. M.K. and H.-H.K. conducted the Raman experiments. M.K., U.W. and A.Y. performed the first-principles calculations. M.O., R.J.G. and R.S. conducted the X-ray absorption spectroscopy experiments. M.K. and H.T. wrote the manuscript, and all authors commented on it.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Materials thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Electronic density of states of Ba0.35K0.65SbO3 and Ba0.35K0.65BiO3.
The results are consistent with those suggested from the molecular-orbital diagrams (Figs. 1c and 1e); Ba0.35K0.65BiO3 with negative ΔCT shows predominant Bi 6s and O 2pσ characters in the spσ and spσ* bands, respectively. The projected density of states (PDOS) of O 2pσ at the Fermi level is larger than that of Bi 6s [PDOS (Bi 6s) / PDOS (O 2pσ) ≅ 0.552]. On the contrary, for Ba0.35K0.65SbO3 with ΔCT slightly positive while close to zero, the ratio between Sb 5s and O 2pσ PDOS is not so different between the spσ and spσ* bands, and very close to unity at the Fermi level [PDOS(Sb 5s) / PDOS (O 2pσ) ≅ 1.06)]. Thus, metal s character with respect to O 2pσ at the Fermi level is stronger in Ba0.35K0.65SbO3 than Ba0.35K0.65BiO3. Total DOS at the Fermi level shows almost no difference between the two compounds (Ba0.35K0.65SbO3: 0.223 states/eV, Ba0.35K0.65BiO3: 0.227 states/eV).
Extended Data Fig. 2 Metal s and oxygen 2p characters of Ba0.35K0.65SbO3 and Ba0.35K0.65BiO3.
The fat-band representations of the band structure of Ba0.35K0.65BiO3 calculated via the hybrid-DFT showing a, Bi 6s, b, O 2pπ, and c, O 2pσ orbital characters. The black dashed circle in a denotes a band at Γ at which Bi 6s (a1g symmetry) do not hybridize with any O 2p states in the cubic structure. The energy of this band can be used to estimate the on-site energy of Bi 6s31,34,35, if one neglects weak Bi 6s–O 2s hybridization. The two black dashed circles in b denote triply degenerate bands at R at which the O 2pπ states have the t2g and t1g symmetries, respectively, and do not hybridize with Bi 6s or 6p states. The on-site energy of O 2pπ can be reasonably approximated by averaging the energies of these two bands, which cancels out the effect of O 2p–O 2p hybridization. The fat-band representations of the electronic band structure of Ba0.35K0.65SbO3 calculated via the hybrid-DFT showing d, Sb 5s, e, O 2pπ, and f, O 2pσ orbital characters. The black dashed circles in d and e denote the bands with Sb 5s (a1g) and O 2pπ t2g and t1g characters as in the case of Ba0.35K0.65BiO3.
Extended Data Fig. 3 The oxygen K-edge X-ray absorption spectra of Ba1-xKxSbO3 (0 ≤ x ≤ 0.75).
a, The spectra of the BKSO samples with various K contents were measured at 300 K in the total fluorescence yield mode. All the samples show the pre-peak structure (black arrows) analogous to the Ba0.35K0.65SbO3 sample depicted in Fig. 4d. This indicates a strong admixture of Sb 5s with O 2p throughout the entire x range, but the intensity of the pre-peak is appreciably reduced compared with that of BKBO at comparable x values41,42,55. The position of the pre-peak shifts to a lower energy with increase of x, which can be understood as the suppression of the CDW gap by doping holes41,55. The high-energy peak (grey arrows) shifts to a higher energy, which may be associated with the Ba 5d and K 3d states that change upon the chemical substitution41. For the x = 0, 0.65, and 0.75 samples, the extra peak around 531 eV (black asterisks) likely originates from a degraded surface, because of its pronounced intensity in the surface-sensitive total electron yield mode data (not shown). Further quantitative analysis has so far been limited at present, as the Sb M5-edge gives rise to an additional structure around the pre-peak because its energy is so close to that of the oxygen K-edge56. b, The spectra of the x = 0.65 sample at 300 and 25 K, showing no apparent change within the temperature range investigated. We note that the x = 0.65 sample shown here is different from that in Fig. 4d.
Supplementary information
Supplementary Information
Supplementary Note 1, Figs. 1–5 and Tables 1–3.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kim, M., McNally, G.M., Kim, HH. et al. Superconductivity in (Ba,K)SbO3. Nat. Mater. 21, 627–633 (2022). https://doi.org/10.1038/s41563-022-01203-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-022-01203-7
This article is cited by
-
Large spin–orbit torque in bismuthate-based heterostructures
Nature Electronics (2023)
-
Local inversion-symmetry breaking in a bismuthate high-Tc superconductor
Nature Communications (2023)
-
A hybrid Monte Carlo study of bond-stretching electron–phonon interactions and charge order in BaBiO3
npj Computational Materials (2023)
-
Origin of superconductivity in hole doped SrBiO3 bismuth oxide perovskite from parameter-free first-principles simulations
npj Computational Materials (2023)
-
Atomic and electronic structures of correlated SrRuO3/SrTiO3 superlattices
Journal of the Korean Physical Society (2023)