Abstract
A large anomalous Nernst effect (ANE) is crucial for thermoelectric energy conversion applications because the associated unique transverse geometry facilitates module fabrication. Topological ferromagnets with large Berry curvatures show large ANEs; however, they face drawbacks such as strong magnetic disturbances and low mobility due to high magnetization. Herein, we demonstrate that YbMnBi2, a canted antiferromagnet, has a large ANE conductivity of ~10 A m−1 K−1 that surpasses large values observed in other ferromagnets (3–5 A m−1 K−1). The canted spin structure of Mn guarantees a non-zero Berry curvature, but generates only a weak magnetization three orders of magnitude lower than that of general ferromagnets. The heavy Bi with a large spin–orbit coupling enables a large ANE and low thermal conductivity, whereas its highly dispersive px/y orbitals ensure low resistivity. The high anomalous transverse thermoelectric performance and extremely small magnetization make YbMnBi2 an excellent candidate for transverse thermoelectrics.
Similar content being viewed by others
Main
Topological electronic structures lay the foundation for new functionalities and are crucial for various applications, including thermoelectric energy conversion1,2,3. In the past few decades, many good longitudinal thermoelectric materials have been demonstrated to be topological insulators4,5. Recently, with the emergence of topological semimetals, the anomalous Nernst effect (ANE) has attracted increasing attention for transverse thermoelectric applications2,3,6,7,8,9,10. Owing to the large Berry curvature near the Fermi energy, large-ANE thermopowers have been achieved in a few topological ferromagnets2,3,6,7,8,9,10,11,12, which show great potential for stable and precise temperature control, particularly in micro- or nanosized devices13,14. For example, Co3Sn2S2 (refs. 7,8), Co2MnGa (refs. 3,9) and Fe3Ga (ref. 2) showed ANE thermopowers of 3–8 μV K−1 and ANE conductivities of 0.5–5 A m−1 K−1, and recently UCo0.8Ru0.2Al (ref. 15) was reported to have a colossal ANE thermopower of 23 μV K−1 and a large ANE conductivity of 15 A m−1 K−1. So far, large ANEs have been reported in only a few topological ferromagnets, and topological noncollinear antiferromagnets have rarely been studied, except for Mn3X (X = Sn and Ge)6,10,12. The search for large ANEs in noncollinear topological antiferromagnets will yield advantages by broadening the material platform for transverse thermoelectrics, as well as revealing novel topological phenomena.
To use the ANE for practical applications, low resistivity and thermal conductivity are also required. Moreover, at the device level, low magnetization and a small inherent stray field are important to eliminate magnetic disturbances and stabilize the remanent magnetization in the in-plane direction if using in a thin-film case16. From these viewpoints, ANE efficiency is coupled with various parameters, similar to the longitudinal Seebeck effect17, and additional magnetization makes the coupling more complicated. For ferromagnets in general, although strong ferromagnetism breaks time-reversal symmetry and offers a large Berry curvature, it also has some drawbacks. With local moment and itinerant electrons (usually due to the heavy d or even f bands) at the Fermi energy (EF), these ferromagnets mostly have relatively low mobility and high resistivity. In addition, the high magnetization and strong inherent stray field of ferromagnets introduce a strong magnetic disturbance, which causes interference with other electronic devices in practical applications.
Herein, considering the challenges outlined above, we highlight the importance of searching for materials with broken time-reversal symmetry and p bands or p–d hybridization near EF. YbMnBi2, as a canted antiferromagnet, can simultaneously realize broken time-reversal symmetry and relatively low resistivity with light band conduction. The canted spin structure at Mn sites breaks time-reversal symmetry. Meanwhile, low resistivity can be achieved owing to the sharp dispersion of the px/y orbitals of Bi. Moreover, the large spin–orbit coupling (SOC) from Bi is critical for band topology, transverse transport response and low thermal conductivity. Furthermore, the YbMnBi2 canted antiferromagnet has much smaller magnetization and inherent stray fields than other ferromagnets. All of these features demonstrate that YbMnBi2 could provide a new material platform beyond ferromagnets for transverse thermoelectric applications.
Canted antiferromagnets for ANE thermoelectric applications
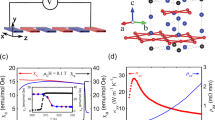
A Nernst device can greatly simplify module fabrication via its unique transverse geometry: the device can be made simply from one material, rather than needing both polarities of charge carriers in separate materials, as is required of Seebeck modules. As schematically shown in Fig. 1a, longitudinal Seebeck thermoelectric devices require coupled p- and n-type legs and assembled pairs17,18. In contrast, the Nernst device (Fig. 1b) offers various advantages that simplify module assembly. First, complex electrical connections and associated electrical resistances are eliminated because it requires only one material. Second, the voltage in Nernst devices can be probed in an isothermal plane, and the electrodes can be constructed at only the isothermal cold end; hence, such devices do not require contacts that are stable at high temperatures. Third, the output of a Nernst device scales extrinsically with the device size: manufacturing longer and thicker devices can increase the voltage output and temperature gradient, respectively. Increasing the size in either dimension would increase the associated potential drop.
a,b, Schematics of thermoelectric devices based on the Seebeck effect (a) and Nernst effect (b). The Nernst device needs only one material and eliminates the complex electrical connections required in the Seebeck device, especially at the hot side. B, magnetic field; E, electrical field; ∇T, temperature gradient. c, Schematics of the band structure near EF for canted YbMnBi2 (left) and general ferromagnets (right). YbMnBi2 shows a much sharper band dispersion and a higher mobility than general ferromagnets.
YbMnBi2 outshines common ferromagnets for applications as a Nernst device in two ways: high mobility and low magnetization. First, as schematically shown in Fig. 1c, the bands of YbMnBi2 at EF are very light in the ab plane, formed by the hybridization of p and d orbitals and thus guaranteeing a high mobility; they are usually heavy d or f orbitals for general ferromagnets. Second, the ferromagnetism originating from the canted spin structure of Mn is extremely weak. These two advantages are useful for thermoelectric applications owing to the low resistivity at the material level and small magnetic disturbance at the device level.
The search for canted antiferromagnets
We have reviewed the magnetic topological materials identified recently by high-throughput calculations19. To introduce a canted spin structure, we examined the manganese pnictides RMnPn2, where R is a rare- or alkaline-earth metal, and Pn is a pnictide (Pn = P, As, Sb or Bi). A few canted manganese pnictides—such as SrMnSb2 (ref. 20), YbMnBi2 (ref. 21) and Ca1−xNaxMnBi2 (ref. 22)—are reported to be magnetic topological materials with a canted spin structure; they are therefore able to hold a non-zero Berry curvature23,24. Moreover, the bands contributed by pnictides are highly dispersive25, which can provide a low resistivity, especially compared with that of ferromagnets.
Given that Yb is relatively stable, Mn has a canted spin structure and Bi can induce large SOC, YbMnBi2 was investigated. As shown in Fig. 2a, YbMnBi2 crystallizes in a P4/nmm structure with two types of Bi: Bi 1 is bonded with Mn and Bi 2 forms an interlayer. The spin of Mn is antiferromagnetic along the c axis but canted in the ab plane. The Néel temperature was reported to be ~290 K (ref. 26), which is very close to that shown in Fig. 2b (~283 K), as also indicated by the turning point in the temperature-dependent resistivity (Supplementary Fig. 1). A clear ferromagnetic transition is observed, as shown in Fig. 2b. The sharp increase in magnetization upon cooling observed in the field cooling curves indicates a spin canting temperature of ~250 K. The field dependence of the magnetization is shown in Supplementary Fig. 2. Below 250 K, the saturation magnetization value is ~1.25 × 10−3 μB per formula unit (f.u.) in the ab plane, suggesting a very small canting angle (θ) of approximately 0.018°. Although the spin canting is very weak and may even be inaccessible in experiments requiring a strong signal26,27, it plays a crucial role in the anomalous thermal/electrical transport by inducing a non-zero Berry curvature.
a, Crystal structure of YbMnBi2. The spin structure is canted at Mn sites, contributing to weak ferromagnetism in the ab plane. b, Temperature dependence of magnetization M in the ab plane (magnetic field B parallel to ab plane, B//ab) and c axis (B parallel to c axis, B//c). Red and magenta curves denote field cooling (FC) under 1 T, whereas blue and green curves denote zero-field cooling (ZFC). The field for both FC and ZFC measurements is 100 Oe. A sharp increase in FC curves upon cooling indicates a spin canting temperature (Tsc) of ~250 K; the Néel temperature (TN) is ~283 K. An extremely small θ of ~0.018° is resolved from the magnetization curves. c, The nodal line (yellow) formed near EF in the kxky plane is shown (kx and ky are the x and y direction in the reciprocal space). The conduction and valence bands are shown in red and blue, respectively. d, Schematic of the EF dependence of the Berry curvature (left), σAHE (middle) and αANE (right). The strength of the Berry curvature depends on EF, resulting in the maximum σAHE when EF is near the Weyl nodes, whereas the maximum αANE lies at a different energy.
Owing to the canted spin structure, YbMnBi2 has unique topological properties. When the SOC is ignored, a nodal line protected by glide-plane symmetry exists in the Brillouin zone because of the band inversion of the px/y orbitals of Bi 2, as shown by the yellow line in Fig. 2c. When SOC is included, the nodal line is gapped, resulting in two pairs of Weyl nodes and a non-zero Berry curvature. The strength of the Berry curvature depends on EF, and reaches its maximum when EF is near the Weyl nodes. As schematically illustrated in Fig. 2d, the shift in EF would probe the strength of the Berry curvature, therefore leading to the varying strength of the anomalous Hall effect (AHE) conductivity (σAHE) and the ANE conductivity (αANE)28,29,30. In this case, it is essential to optimize EF to observe a large σAHE or αANE, which are usually related to the quality of the single crystal.
According to theory, under a spin canting direction of (110)21, the magnetic point group of YbMnBi2 becomes m′m2′, and only transverse transport signals in the ac/bc and ca/cb configurations can be observed owing to mirror symmetry31. Taking the cb configuration as an example, this implies that the transverse signal is measured along the c axis while a temperature gradient is applied along the b axis and a magnetic field along the a axis. Experimental results are highly consistent with theoretical predictions: both the ANE and AHE are observed in the bc and cb configurations, but not in the ab plane (Supplementary Figs. 3 and 4). The non-zero Berry curvature is thus believed to be an essential cause of the ANE/AHE.
Anomalous Nernst thermopower and anomalous Hall resistivity
The ANE thermopower (SANE) and AHE resistivity (ρAHE) (with Gerlach’s sign convention, as illustrated in Supplementary Fig. 5) in the cb and bc configurations show qualitatively identical behaviour but different values. SANE and ρAHE in both the cb (Fig. 3a,b) and bc (Fig. 3c,d) configurations saturate at ~1 T, which is relatively small, comparable to the saturation field of Co2MnGa3,9, and much lower than Fe3Ga (~2 T)2. SANE first increases and then decreases with heating, showing a peak at ~160 K (Fig. 3e); in contrast, ρAHE increases up to ~200 K (Fig. 3f). The maximum SANE values are ~6 µV K−1 and ~3 µV K−1 at 160 K in the cb and bc configurations, respectively, which is relatively large, especially for an antiferromagnet. This is remarkable, as the largest ANE signals reported so far in the antiferromagnets observed were ~0.5 µV K−1 in Mn3Sn (refs. 6,12) and ~1.2 µV K−1 in Mn3Ge (refs. 10,32).
a–d, The magnetic field dependence of SANE (a,c) and ρAHE (b,d) in cb (V//c) for a and b, and bc (V//b) for c and d for the temperatures indicated. Herein, cb indicates the measurement of the Nernst/Hall voltage along the c axis and application of the temperature gradient along the b axis, and vice versa for bc; the magnetic field B is always along the a axis. The configuration of B, ∇T/I and V is schematically shown in the insets. I, current; V, voltage. e,f, The temperature dependence of the absolute values of SANE (e) and ρAHE (f), respectively, is shown at B = 1 T from 40 to 250 K. Directions of B, ∇T/I and V are parallel to the a, b and c axis, respectively, for cb and bc, as indicated by the notation in the figure.
Intrinsic and extrinsic effects on ANE/AHE conductivity
To quantitatively understand the origin of the ANE and AHE in YbMnBi2, αANE and σAHE were analysed with first-principles calculations assuming θ = 10°. As αANE is an energy derivative of σAHE (ref. 24), we first investigated σAHE, followed by αANE. Two characteristics of the band structure are essential to understand the AHE and ANE. First, the hole pocket near the Г point, which stems from the hybridization of the pz orbitals of Bi 1 and the d orbitals of Mn, should be far below EF if θ is zero (Supplementary Fig. 6), but above EF if θ is non-zero (Fig. 4a). The hole pocket near the Г point can generate a negative Berry curvature31, which enhances the total Berry curvature as the electron pockets (along Г–M, Г–X and Г–Y, originating from the px/y orbitals of Bi 2) also generate a negative Berry curvature (Fig. 4b). As shown in Fig. 4c, the Fermi surface at the Г point is observed in our crystal by angle-resolved photoemission spectroscopy (ARPES), which is highly important as it demonstrates the non-zero θ and additional negative Berry curvature from the Г band. The larger θ is, the more contribution to band conduction generated at the Г point, as illustrated on the right side of Fig. 4c and Supplementary Fig. 7. Figure 4d plots |σAHE| as a function of θ; the calculated |σAHE| has a nearly linear dependence on θ from 8° to 16°. As σAHE is 0 if θ = 0°, we extrapolated σAHE to 0 in the simplest way (with a linear dotted line), which therefore allowed us to roughly assess σAHE at extremely small θ.
a,b, Band structure of YbMnBi2 (a) (in which the different coloured lines denote the contribution from different orbitals from Mn and Bi elements) and Berry curvature distribution (b) in the Brillouin zone calculated from first principles by assuming θ = 10°. The total Berry curvature contribution from the electron pockets is negative. With a larger spin θ, the d orbitals of Mn join the conduction, and an additional negative Berry curvature is generated at the Г point. c, Left: ARPES intensity at EF as a function of the ab plane wavevectors (kx and ky) measured with 55 eV photons at T = 19 K. The ARPES intensity is integrated over the energy range of +10 meV to −10 meV with respect to EF. The inset shows two pairs of Weyl nodes. Right: the calculated band variation at the Г point with increasing θ. d, Calculated |σAHE| as a function of θ. The solid line shows the calculated results, and the dashed line shows a linear extrapolation. e,f, Experimental results for the temperature dependence of |σAHE| (e) and |αANE| (f) in cb (V//c) and bc (V//b). Calculated |αANE| values at different EF are shown by the dashed lines in f.
Second, as the electronic bands of YbMnBi2 are strongly anisotropic and highly dispersive in the ab plane (Supplementary Fig. 8), there can be a large shift in EF. In fact, such a shift was observed in the Hall resistivity (Supplementary Fig. 4c): a transition from n-type to p-type was observed from 50 to 100 K. Such high anisotropy was also observed in the Seebeck coefficient (Supplementary Fig. 9), where positive and negative values coexisted in different crystallographic directions—this may indicate that YbMnBi2 is a goniopolar material33. This strong anisotropy makes it challenging to determine the actual EF in specific directions as it can vary in different directions. On the basis of the analysis above, we attained a better understanding of |σAHE| and |αANE|.
As shown in Fig. 4e, the maximum experimental |σAHE| can be matched with the theoretically predicted result with a very small θ (as illustrated by the point indicated with green lines in Fig. 4d). The decreasing trend above ~150 K can be attributed to the temperature disturbance of the spin structure; however, the increasing trend below 150 K is atypical. |αANE| also shows an unusual decreasing trend, as shown in Fig. 4f. In addition, anisotropic behaviours are observed in σAHE and αANE. Akgoz and Saunders34,35 combined the reciprocity relations with the crystal symmetries to derive the allowed symmetry operations in various point groups. With the magnetic point group of YbMnBi2 being m′m2′, one would expect that the Hall resistivity ρbc(Ha) = −ρcb(−Ha) (here, ρbc and ρcb are the Hall resistivity in bc and cb, respectively, and Ha is the external field along the a axis)34 and the same relation would be expected to hold for the conductivity tensors. The fact that this is not observed in Fig. 4e points to the absence of time-reversal symmetry and the anomalous origin of the Hall conductivities. For the thermoelectric conductivity tensor, the observation that Sbc(Ha) ≠ −Scb(−Ha) (Fig. 3e) and αbc(Ha) ≠ −αcb(−Ha) (Fig. 4f) is allowed35. Most importantly, a maximum |αANE| of 10 A m−1 K−1 was achieved in the bc configuration, which is much higher than those of most of the ferromagnets, including Co3Sn2S2 (ref. 7), Co2MnGa (ref. 9), Fe3Ga (ref. 2) and SmCo5 (ref. 36; the record value for which is ~5 A m−1 K−1) and one order of magnitude higher than those of the antiferromagnets Mn3X (X = Sn (refs. 6,12) and Ge (refs. 10,32)).
There could be extrinsic contributions to such a large αANE in addition to the Berry curvature, particularly considering the following three aspects. First, there is a mismatch between the experimental results and those from first-principles predictions. The calculated |αANE| is much lower than the experimental αbc, even when EF was optimized (Supplementary Fig. 10). The negative temperature dependence of |αANE| is similar to that recently been observed in MnBi, which was attributed to an extrinsic magnon-drag effect and could account for the deviation in temperature dependence between experiment and theory37. Second, anisotropic behaviour was observed in αANE; that is, αbc ≠ −αcb. In principle, from density functional theory, αbcintrinsic = −αcbintrinsic only if it solely originated from the Berry curvature, as determined by the Berry phase of the wavefunction, Ωij(k) = −Ωji(k). Third, a large violation of the ratio of |αbc/σbc| from an empirical value of kB/e (where kB is the Boltzmann constant) was observed (Supplementary Fig. 11). As recently argued by Ding et al. and Xu et al., the ratio of |αANE/σANE| saturates to ~kB/e at 300 K if both originate from intrinsic Berry curvature8,38.
In fact, extrinsic contributions are possible in real crystals owing to the unavoidable presence of scattering—particularly for systems with large SOC, which is the case for YbMnBi2. The large SOC induces an additional skew force on the spin-polarized charge carriers39,40. Previous materials with large ANEs, including Co3Sn2S27, Co2MnGa9, Fe3Ga2 and Mn3X (X = Sn and Ge)6,10,12,32, have small SOC without heavy elements, which is not the case here. Very recently, Papaj and Fu41 indicated that extrinsic contributions can be dramatic, and even potentially dominant over Berry curvature. To accurately describe αANE, vast improvements to current modelling techniques, beyond the simple single band models, are necessary. Such improvements include, but are not limited to, the modelling of band anisotropy, deviations from a linear band dispersion and interactions of point defects with electrons41. The strong band anisotropy in YbMnBi2 has rarely been observed in other materials with large ANEs. We highlight that the strong anisotropy in the Fermi surface of YbMnBi2 plays a critical role in achieving large αANE in the bc configuration and not in the cb configuration. The electron pockets are highly dispersive in the ab plane but have nearly no dispersion along the c axis, leading to a considerable difference in the extrinsic scattering effects on charge carriers between the bc and cb configurations. The extremely high σbb (which is ~35 times higher than σcc at 80 K), along with asymmetric skew scattering rates, results in large αANE in only the bc configuration. Future investigations are warranted to explore both the intrinsic (for example, by developing a detailed distribution of the Berry curvature in the Brillouin zone) and extrinsic (for example, by measuring the strength of the skew scattering and side jump related to the SOC) contributions to the large αANE in more detail.
Beyond the ANE
In addition to the large ANE signals, YbMnBi2 presents extremely small magnetization M, which can reduce the interaction of the magnetic field with surrounding electronic devices during practical applications. Figure 5a compares |αANE|/M, |SANE|/M and M of YbMnBi2 with those of other compounds with large SANE—namely, the ferromagnets Fe3Ga (ref. 2), Co2MnGa (refs.3,9), Co3Sn2S2 (ref. 7), UCo0.8Ru0.2Al (ref. 15), MnBi (ref. 37) and Ga1−xMnxAs (ref. 42) and the chiral antiferromagnets Mn3Sn (refs. 6,12) and Mn3Ge (refs. 10,32). The noncollinear antiferromagnets, especially YbMnBi2, clearly surpass all of the ferromagnets in terms of |αANE|/M and |SANE|/M, demonstrating that canted antiferromagnets, even with extremely low magnetization, can display a large ANE that competes with the best ferromagnets. For practical applications, using permanent magnets (with which fields of 0.3 T are common, and 1 T is possible with a careful choice of materials) is reasonable for materials with no remanent magnetization, such as YbMnBi2. Further exploration of the zero-field ANEs of polycrystals and/or thin films would be of interest for future devices.
a, Comparison of the absolute values of |αANE|/M, |SANE|/M and M of YbMnBi2 in the bc configuration (160 K) with those of other compounds with large ANE thermopowers—namely, the ferromagnets Fe3Ga (300 K)2, Co2MnGa (300 K)3,9, Co3Sn2S2 (80 K)7, UCo0.8Ru0.2Al (40 K)15, MnBi (80 K)37, Ga1−xMnxAs (10 K)42, and the chiral antiferromagnets Mn3Sn (300 K)6,12 and Mn3Ge (300 K)10,32. Antiferromagnets are marked as AFM, and other materials are all ferromagnets. b, The temperature dependence of zTANE values for YbMnBi2 in the bc configuration compared with those of other compounds with large ANE thermopowers.
In addition to the large ANE signals (owing to the anisotropy), the resistivity and thermal conductivity can be decoupled to realize simultaneous gains in both—that is, low ρbb and low κcc (κcc is the thermal conductivity along the c axis) (Supplementary Fig. 1). Both ρbb and κcc are much lower than the values for the ferromagnets with a large ANE (Supplementary Table 1). Consequently, YbMnBi2 shows a high anomalous Nernst thermoelectric figure of merit zTANE, defined as, zTANE,bc = SANE,bc2T/(ρbbκcc). As shown in Fig. 5b, YbMnBi2 has high zTANE values over a wide temperature range, demonstrating its highly promising anomalous transverse thermoelectric performance. Although the zTANE values are still much lower than the traditional, longitudinal zT, we present this result as promising progress towards the use of the ANE in thermoelectric applications, which could ultimately offer improvements in microscale devices and the field of spin caloritronics.
Outlook
In summary, YbMnBi2, a canted antiferromagnet, breaks time-reversal symmetry and yields a non-zero Berry curvature. Alongside the large SOC contributed by the heavy Bi atoms, a large ANE conductivity of 10 A m−1 K−1 was observed, which is two to three times larger than those of most of the ferromagnets and compares favourably with those of noncollinear antiferromagnets. This is of great interest, particularly considering its small magnetization. Furthermore, it shows strong anisotropy, making it possible to achieve low resistivity and low thermal conductivity simultaneously in transverse thermoelectric configurations. All of these unique features demonstrate the great potential of YbMnBi2 as a transverse thermoelectric material.
These results suggest that canted antiferromagnets, including (but not limited to) the RMnPn2 family, are worthy of further investigation for large ANEs. Future studies searching for compounds with canting temperatures higher than room temperature are crucial. Moreover, investigating the use of polycrystalline or thin-film materials to induce remanent magnetizations could be important for practical applications without external magnetic fields. Precise tuning of the Fermi level would also be an efficient way to enhance the ANE. Finally, with a deeper understanding of the intrinsic and extrinsic contributions to the ANE, both experimentally and theoretically, we expect to achieve boosted ANEs in more topological materials.
Methods
Ab initio calculations
Calculations were conducted using density functional theory implemented in the Vienna ab initio simulation package (VASP) code43,44. To calculate the band structure, the Perdew–Burke–Ernzerhof exchange-correlation functional and projector-augmented-wave approach were used. The cut-off energy was set at 500 eV to expand the wavefunctions into a plane–wave basis. The Brillouin zone was sampled in the k-space within the Monkhorst–Pack scheme45, and a k mesh of 10 × 10 × 4 was adopted based on an equilibrium structure. The C-type antiferromagnetic order along the c axis at the Mn sites, a canted spin structure and SOC were considered. To calculate the anomalous Hall conductivity and anomalous Nernst conductivity, the ab initio density functional theory Bloch wavefunction was projected onto highly symmetric atomic-orbital-like Wannier functions46 with a diagonal position operator using VASP code43,44. To obtain precise Wannier functions, we included the outermost s and d orbitals for Yb, d orbital for Mn and p orbital for Bi to cover the full band overlap from the ab initio and Wannier functions. The atomic coordinates for the electronic structure calculations are shown in Supplementary Table 2.
Sample preparation
YbMnBi2 single crystals were grown using a self-flux method with an elemental ratio of Yb:Mn:Bi of 1:1:4. Yb (99.99%), Mn (99.98%) and Bi (99.999%) were cut into small pieces and mixed before being placed in an alumina crucible. They were then sealed in a quartz tube under a partial argon pressure. The sealed tube was heated to 1,050 °C over 2.5 days and maintained at that tempearture for 24 h. Next, it was slowly cooled to 400 °C at a rate of 2 °C h−1, and single crystals were obtained by removing the flux through centrifugation.
Sample characterization
The single crystallinity and orientation of the as-grown single crystals were determined using Laue X-ray diffraction (Supplementary Fig. 12). The composition and homogeneity were examined by scanning electron microscopy (Philips XL30) with an Oxford energy-dispersive X-ray spectroscopy (Quantax, Bruker) (Supplementary Fig. 13).
ARPES measurements
The ARPES experiment was performed at the Bloch beamline at MAX IV with a Scienta DA30 analyser. The sample was cleaved in situ at 19 K with a base pressure lower than 1 × 10−10 mbar.
Measurement of transport properties
Resistivities and Hall resistivities were measured using a physical property measurement system (PPMS9, Quantum Design) in an electrical transport option via a standard four-probe method. The Nernst thermopower, Seebeck coefficient and thermal conductivity were measured in the PPMS9 under a high vacuum by using a standard four-contact steady-state method47. The magnetization was measured using a magnetic property measurement system (MPMS3, Quantum Design).
Data availability
All the data supporting the plots within this paper and the findings of this study are available from the corresponding author upon request.
References
Narang, P., Garcia, C. A. C. & Felser, C. The topology of electronic band structures. Nat. Mater. 20, 293–300 (2021).
Sakai, A. et al. Iron-based binary ferromagnets for transverse thermoelectric conversion. Nature 581, 53–57 (2020).
Sakai, A. et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal. Nat. Phys. 14, 1119–1124 (2018).
Heremans, J. P., Cava, R. J. & Samarth, N. Tetradymites as thermoelectrics and topological insulators. Nat. Rev. Mater. 2, 17049 (2017).
He, J. & Tritt, T. M. Advances in thermoelectric materials research: looking back and moving forward. Science 357, eaak9997 (2017).
Ikhlas, M. et al. Large anomalous Nernst effect at room temperature in a chiral antiferromagnet. Nat. Phys. 13, 1085–1090 (2017).
Guin, S. N. et al. Zero-field Nernst effect in a ferromagnetic kagome-lattice Weyl-semimetal Co3Sn2S2. Adv. Mater. 31, 1806622 (2019).
Ding, L. et al. Intrinsic anomalous Nernst effect amplified by disorder in a half-metallic semimetal. Phys. Rev. X 9, 041061 (2019).
Guin, S. N. et al. Anomalous Nernst effect beyond the magnetization scaling relation in the ferromagnetic Heusler compound Co2MnGa. NPG Asia Mater. 11, 16 (2019).
Wuttke, C. et al. Berry curvature unravelled by the anomalous Nernst effect in Mn3Ge. Phys. Rev. B 100, 085111 (2019).
Liang, T. et al. Anomalous Nernst effect in the Dirac semimetal Cd3As2. Phys. Rev. Lett. 118, 136601 (2017).
Li, X. et al. Anomalous Nernst and Righi-Leduc effects in Mn3Sn: Berry curvature and entropy flow. Phys. Rev. Lett. 119, 056601 (2017).
Mao, J., Chen, G. & Ren, Z. Thermoelectric cooling materials. Nat. Mater. 20, 454–461 (2020).
Semenyuk, V. in Thermoelectrics Handbook: Macro to Nano (ed. Rowe, D.M.) Ch. 58 (Taylor & Francis, 2006).
Asaba, T. et al. Colossal anomalous Nernst effect in a correlated noncentrosymmetric kagome ferromagnet. Sci. Adv. 7, eabf1467 (2021).
Uchida, K., Zhou, W. & Sakuraba, Y. Transverse thermoelectric generation using magnetic materials. Appl. Phys. Lett. 118, 140504 (2021).
Snyder, G. J. & Toberer, E. S. Complex thermoelectric materials. Nat. Mater. 7, 101–110 (2008).
Bell, L. E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 12, 1457–1461 (2008).
Xu, Y. et al. High-throughput calculations of magnetic topological materials. Nature 586, 702–707 (2020).
Liu, J. Y. et al. A magnetic topological semimetal Sr1−yMn1−zSb2 (y, z < 0.1). Nat. Mater. 16, 905–910 (2017).
Borisenko, S. et al. Time-reversal symmetry breaking type-II Weyl state in YbMnBi2. Nat. Commun. 10, 3424 (2019).
Yang, R. et al. Spin-canting-induced band reconstruction in the Dirac material Ca1−xNaxMnBi2. Phys. Rev. Lett. 124, 137201 (2020).
Yan, B. & Felser, C. Topological materials: Weyl semimetals. Annu. Rev. Condens. Matter Phys. 8, 337–354 (2017).
Xiao, D., Yao, Y., Fang, Z. & Niu, Q. Berry-phase effect in anomalous thermoelectric transport. Phys. Rev. Lett. 97, 026603 (2006).
Pan, Y. et al. Thermoelectric properties of novel semimetals: a case study of YbMnSb2. Adv. Mater. 33, 2003168 (2021).
Soh, J.-R. et al. Magnetic structure and excitations of the topological semimetal YbMnBi2. Phys. Rev. B 100, 144431 (2019).
Wang, A. et al. Magnetotransport study of Dirac fermions in YbMnBi2 antiferromagnet. Phys. Rev. B 94, 165161 (2016).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2009).
Noky, J., Zhang, Y., Gooth, J., Felser, C. & Sun, Y. Giant anomalous Hall and Nernst effect in magnetic cubic Heusler compounds. npj Comput. Mater. 6, 77 (2020).
Le, C., Felser, C. & Sun, Y. Design strong anomalous Hall effect via spin canting in antiferromagnetic nodal line materials. Phys. Rev. B 104, 125145 (2021).
Xu, L. et al. Finite-temperature violation of the anomalous transverse Wiedemann-Franz law. Sci. Adv. 6, eaaz3522 (2020).
He, B. et al. The Fermi surface geometrical origin of axis-dependent conduction polarity in layered materials. Nat. Mater. 18, 568–572 (2019).
Akgoz, Y. C. & Saunders, G. A. Space-time symmetry restrictions on the form of transport tensors. I. Galvanomagnetic effects. J. Phys. C 8, 1387–1396 (1975).
Akgoz, Y. C. & Saunders, G. A. Space-time symmetry restrictions on the form of transport tensors. II. Thermomagnetic effects. J. Phys. C 8, 2962–2970 (1975).
Miura, A. et al. Observation of anomalous Ettingshausen effect and large transverse thermoelectric conductivity in permanent magnets. Appl. Phys. Lett. 115, 222403 (2019).
He, B. et al. Large magnon-induced anomalous Nernst effect in single-crystal MnBi. Joule https://doi.org/10.1016/j.joule.2021.08.007 (2021).
Xu, L. et al. Anomalous transverse response of Co2MnGa and universality of the room-temperature αijA/σijA ratio across topological magnets. Phys. Rev. B 101, 180404(R) (2020).
Jin, H., Yang, Z., Myers, R. C. & Heremans, J. P. Spin-Seebeck like signal in ferromagnetic bulk metallic glass without platinum contacts. Solid State Commun. 198, 40–44 (2014).
Watzman, S. J. et al. Magnon-drag thermopower and Nernst coefficient in Fe, Co, and Ni. Phys. Rev. B 94, 144407 (2016).
Papaj, M. & Fu, L. Enhanced anomalous Nernst effect in disordered Dirac and Weyl materials. Phys. Rev. B 103, 075424 (2021).
Pu, Y. et al. Mott relation for anomalous Hall and Nernst Effects in Ga1-xMnxAs ferromagnetic semiconductors. Phys. Rev. Lett. 101, 117208 (2008).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Yates, J. R., Wang, X., Vanderbilt, D. & Souza, I. Spectral and Fermi surface properties from Wannier interpolation. Phys. Rev. B 75, 195121 (2007).
Heremans, J. P., Thrush, C. M. & Morelli, D. T. Thermopower enhancement in lead telluride nanostructures. Phys. Rev. B 70, 115334 (2004).
Acknowledgements
This work was supported by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Projektnummer 392228380, ERC Advanced grant number 742068 ‘TOP-MAT’ and the European Union’s Horizon 2020 research and innovation programme (grant number 766566; ‘ASPIN’). Y.P. acknowledges financial support from the Alexander von Humboldt Foundation. S.J.W. acknowledges support from the US Department of Energy, Office of Science, Office of Basic Energy Sciences Early Career Research Program (award number DE-SC0020154). J.P.H. acknowledges support from the US Army Research Office (grant number W911NF2120089). We thank B. Thiagarajan and C. Polley for their help with the ARPES experiments.
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
Y.P. grew the single crystal and conducted the crystallinity and composition characterization. Y.P. and S.J.W. designed the experiments. Y.P. and B.H. measured the transport properties. C.L. and Y.S. completed the theoretical calculations. M.Y. performed the ARPES experiments. Y.P., B.H., S.J.W., J.G., J.P.H. and C.F. discussed the results. J.P.H. and C.F. supervised the project. All authors contributed to the preparation of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Materials thanks Kamran Behnia, Qihang Liu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–13, Tables 1 and 2, Discussion and refs. 1–16.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pan, Y., Le, C., He, B. et al. Giant anomalous Nernst signal in the antiferromagnet YbMnBi2. Nat. Mater. 21, 203–209 (2022). https://doi.org/10.1038/s41563-021-01149-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-021-01149-2
This article is cited by
-
Unconventional anomalous Hall effect and large anomalous Nernst effect in antiferromagnet SmMnBi2
Communications Materials (2024)
-
Bipolarity of large anomalous Nernst effect in Weyl magnet-based alloy films
Nature Physics (2024)
-
Bipolar transverse thermopower and low thermal conductivity for an anomalous Nernst-type heat flux sensor in GdCo alloys
Scientific Reports (2024)
-
Large transverse thermoelectric effect induced by the mixed-dimensionality of Fermi surfaces
Nature Communications (2024)
-
The discovery of three-dimensional Van Hove singularity
Nature Communications (2024)