Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Coupled liquid crystalline oscillators in Huygens’ synchrony

Nature Materials volume 20, pages 1702–1706 (2021)Cite this article

Subjects

Abstract

In the flourishing field of soft robotics, strategies to embody communication and collective motion are scarce. Here we report the synchronized oscillations of thin plastic actuators by an approach reminiscent of the synchronized motion of pendula and metronomes. Two liquid crystalline network oscillators fuelled by light influence the movement of one another and display synchronized oscillations in-phase and anti-phase in a steady state. By observing entrainment between the asymmetric oscillators we demonstrate the existence of coupling between the two actuators. We qualitatively explain the origin of the synchronized motion using a theoretical model and numerical simulations, which suggest that the motion can be tuned by the mechanical properties of the coupling joint. We thus anticipate that the complex synchronization phenomena usually observed in rigid systems can also exist in soft polymeric materials. This enables the use of new stimuli, featuring an example of collective motion by photo-actuation.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Synchronized light-induced oscillation of coupled LCN films.
Fig. 2: Entrainment of asymmetric oscillators.
Fig. 3: Modelling of the coupled oscillators.

Data availability

The data that support the findings of this study are available within the article and its Supplementary Information files, and from the corresponding authors upon reasonable request.

References

  1. Whitesides, G. M. Soft robotics. Angew. Chem. Int. Ed. 57, 4258–4273 (2018).

    Article  CAS  Google Scholar 

  2. Zhang, X. et al. The pathway to intelligence: using stimuli-responsive materials as building blocks for constructing smart and functional systems. Adv. Mater. 31, e1804540 (2019).

    Article  Google Scholar 

  3. Yu, Y. & Ikeda, T. Soft actuators based on liquid-crystalline elastomers. Angew. Chem. Int. Ed. 45, 5416–5418 (2006).

    Article  CAS  Google Scholar 

  4. Hines, L., Petersen, K., Lum, G. Z. & Sitti, M. Soft actuators for small-scale robotics. Adv. Mater. 29, 1603483 (2017).

    Article  Google Scholar 

  5. Martella, D., Nocentini, S., Parmeggiani, C. & Wiersma, D. S. Self-regulating capabilities in photonic robotics. Adv. Mater. Technol. 4, 1800571 (2019).

    Google Scholar 

  6. Zeng, H., Wasylczyk, P., Wiersma, D. S. & Priimagi, A. Light robots: bridging the gap between microrobotics and photomechanics in soft materials. Adv. Mater. 30, 1703554 (2018).

    Article  Google Scholar 

  7. Hu, Y., Li, Z., Lan, T. & Chen, W. Photoactuators for direct optical-to-mechanical energy conversion: from nanocomponent assembly to macroscopic deformation. Adv. Mater. 28, 10548–10556 (2016).

    Article  CAS  Google Scholar 

  8. Pikovsky, A., Rosenblum, M. & Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences (Cambridge Univ. Press, 2001).

  9. Vicsek, T. & Zafeiris, A. Collective motion. Phys. Rep. 517, 71–140 (2012).

    Article  Google Scholar 

  10. Boccaletti, S. (ed.) The Synchronized Dynamics of Complex Systems (Monograph Series on Nonlinear Science and Complexity) Vol. 6 (Elsevier, 2008).

  11. O’Keeffe, K. P., Hong, H. & Strogatz, S. H. Oscillators that sync and swarm. Nat. Commun. 8, 1504 (2017).

    Article  Google Scholar 

  12. Huygens, C. Oeuvres complètes de Christiaan Huygens. L’horloge à pendule de 1651 à 1666. Travaux divers de physique, de mécanique et de technique de 1650 à 1666. Traité des couronnes et des parhélies (1662 ou 1663) (La Société hollandaise des sciences, 1888).

  13. Bennett, M., Schatz, M. F., Rockwood, H. & Wiesenfeld, K. Huygens’s clocks. Proc. R. Soc. A Math. Phys. Eng. Sci. 458, 563–579 (2002).

    Article  Google Scholar 

  14. Peña Ramirez, J., Olvera, L. A., Nijmeijer, H. & Alvarez, J. The sympathy of two pendulum clocks: Beyond Huygens’ observations. Sci. Rep. 6, 23580 (2016).

    Article  Google Scholar 

  15. Ikeguchi, T. & Shimada, Y. Analysis of synchronization of mechanical metronomes. In Proc. 5th International Conference on Applications in Nonlinear Dynamics (eds In, V. et al.) 141–152 (Springer, 2019).

  16. Rubenstein, M. et al. Programmable self-assembly in a thousand-robot swarm. Science 345, 795–799 (2014).

    Article  CAS  Google Scholar 

  17. Li, S. et al. Particle robotics based on statistical mechanics of loosely coupled components. Nature 567, 361–365 (2019).

    Article  CAS  Google Scholar 

  18. Justus, K. B. et al. A biosensing soft robot: autonomous parsing of chemical signals through integrated organic and inorganic interfaces. Sci. Robot. 4, eaax0765 (2019).

    Article  Google Scholar 

  19. Ciui, B. et al. Chemical sensing at the robot fingertips: toward automated taste discrimination in food samples. ACS Sens. 3, 2375–2384 (2018).

    Article  CAS  Google Scholar 

  20. Korevaar, P. A. et al. Non-equilibrium signal integration in hydrogels. Nat. Commun. 11, 386 (2020).

    Article  CAS  Google Scholar 

  21. Martella, D. et al. Photonic microhand with autonomous action. Adv. Mater. 29, 1704047 (2017).

    Article  Google Scholar 

  22. Wani, O. et al. A light-driven artificial flytrap. Nat. Commun. 8, 15546 (2017).

    Article  CAS  Google Scholar 

  23. Byun, J. et al. Electronic skins for soft, compact, reversible assembly of wirelessly activated fully soft robots. Sci. Robot. 3, eaas9020 (2018).

    Article  Google Scholar 

  24. Yang, J. C. et al. Electronic skin: recent progress and future prospects for skin-attachable devices for health monitoring, robotics, and prosthetics. Adv. Mater. 31, 1904765 (2019).

    Article  CAS  Google Scholar 

  25. Zhang, M. et al. Synchronization of micromechanical oscillators using light. Phys. Rev. Lett. 109, 233906 (2012).

    Article  Google Scholar 

  26. White, T. J. & Broer, D. J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 14, 1087–1098 (2015).

    Article  CAS  Google Scholar 

  27. Gelebart, A. H., Vantomme, G., Meijer, E. W. & Broer, D. J. Mastering the photothermal effect in liquid crystal networks: a general approach for self-sustained mechanical oscillators. Adv. Mater. 29, 1606712 (2017).

    Article  Google Scholar 

  28. Vantomme, G., Gelebart, A. H., Broer, D. J. & Meijer, E. W. Self-sustained actuation from heat dissipation in liquid crystal polymer networks. J. Polym. Sci. Part A Polym. Chem. 56, 1331–1336 (2018).

    Article  CAS  Google Scholar 

  29. White, T. J. et al. A high frequency photodriven polymer oscillator. Soft Matter 4, 1796–1798 (2008).

    Article  CAS  Google Scholar 

  30. Vantomme, G., Gelebart, A. H., Broer, D. J. & Meijer, E. W. A four-blade light-driven plastic mill based on hydrazone liquid-crystal networks. Tetrahedron 73, 4963–4967 (2017).

    Article  CAS  Google Scholar 

  31. Cafferty, B. J. et al. Robustness, entrainment, and hybridization in dissipative molecular networks, and the origin of life. J. Am. Chem. Soc. 141, 8289–8295 (2019).

    Article  CAS  Google Scholar 

  32. Peña Ramirez, J., Fey, R. H. B., Aihara, K. & Nijmeijer, H. An improved model for the classical Huygens’ experiment on synchronization of pendulum clocks. J. Sound Vib. 333, 7248–7266 (2014).

    Article  Google Scholar 

  33. Shimamura, A. et al. Simultaneous analysis of optical and mechanical properties of cross-linked azobenzene-containing liquid-crystalline polymer films. ACS Appl. Mater. Interfaces 3, 4190–4196 (2011).

    Article  CAS  Google Scholar 

  34. Merindol, R. & Walther, A. Materials learning from life: Concepts for active, adaptive and autonomous molecular systems. Chem. Soc. Rev. 46, 5588–5619 (2017).

    Article  CAS  Google Scholar 

  35. Dattler, D. et al. Design of collective motions from synthetic molecular switches, rotors, and motors. Chem. Rev. 120, 310–433 (2020).

    Article  CAS  Google Scholar 

  36. Leira-Iglesias, J., Tassoni, A., Adachi, T., Stich, M. & Hermans, T. M. Oscillations, travelling fronts and patterns in a supramolecular system. Nat. Nanotechnol. 13, 1021–1027 (2018).

    Article  CAS  Google Scholar 

  37. Boekhoven, J., Hendriksen, W. E., Koper, G. J. M., Eelkema, R. & Van Esch, J. H. Transient assembly of active materials fueled by a chemical reaction. Science 349, 1075–1079 (2015).

    Article  CAS  Google Scholar 

  38. Vantomme, G., Gelebart, A. H., Broer, D. J. & Meijer, E. W. Preparation of liquid crystal networks for macroscopic oscillatory motion induced by light. J. Vis. Exp. 127, e56266 (2017).

    Google Scholar 

Download references

Acknowledgements

This work was financially supported by The Netherlands Organization for Scientific Research (NWO-TOP PUNT grant no. 10018944 and NWO-VENI grant no. 722.017.003), Dutch Ministry of Education, Culture and Science (Gravity Programme grant no. 024.001.035) and the European Research Council (Vibrate ERC grant no. 669991).

Author information

Authors and Affiliations

  1. Institute for Complex Molecular Systems, Eindhoven University of Technology, Eindhoven, the Netherlands

    Ghislaine Vantomme, Anne Helene Gelebart, E. W. Meijer, Henk Nijmeijer & Dirk J. Broer

  2. Department of Chemical Engineering and Chemistry, Laboratory of Macromolecular and Organic Chemistry, Eindhoven University of Technology, Eindhoven, the Netherlands

    Ghislaine Vantomme & E. W. Meijer

  3. Department of Mechanical Engineering, Dynamics and Control, Eindhoven University of Technology, Eindhoven, the Netherlands

    Lars C. M. Elands, Alexander Y. Pogromsky & Henk Nijmeijer

  4. Department of Chemical Engineering and Chemistry, Laboratory for Functional Organic Materials and Devices, Eindhoven University of Technology, Eindhoven, the Netherlands

    Anne Helene Gelebart & Dirk J. Broer

  5. Department of Control Systems and Industrial Robotics, Saint-Petersburg National Research University of Information Technologies Mechanics and Optics, Petersburg, Russia

    Alexander Y. Pogromsky

Authors
  1. Ghislaine Vantomme
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lars C. M. Elands
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Anne Helene Gelebart
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. E. W. Meijer
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Alexander Y. Pogromsky
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Henk Nijmeijer
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Dirk J. Broer
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

G.V., E.W.M. and D.J.B. conceived and planned the project. G.V. and A.H.G. performed the experiments. L.C.M.E. performed the simulations. D.J.B., H.N., A.Y.P. and E.W.M. supervised the effort. G.V. wrote the manuscript. All authors discussed the results and commented on the manuscript.

Corresponding authors

Correspondence to Ghislaine Vantomme or Dirk J. Broer.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

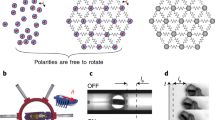
Extended Data Fig. 1 Thermal oscillation.

a,b, Temperature of the coupled LCN films during in-phase oscillation (a) and anti-phase oscillation (b). c, Picture of the thermogram with the two points A and B where the temperatures are measured. The temperature at point A is the blue trace and at point B is the orange trace. The films geometry is 20 mm × 4 mm × 20 µm and are connectively separated by 2 mm.

Extended Data Fig. 2 Thermal conductivity.

a, Scheme of the LCN film positioned on a hot plate at 63 °C. b, Temperature profile over the length of the film showing the poor thermal conductivity of the LCN.

Extended Data Fig. 3 Modeling of the stiffness and damping parameters.

Tensile moduli of the LCN film as a function of temperature (red traces) and their modeled fits (black traces).

Extended Data Fig. 4 Modeling of the actuation torque with temperature.

Displacement of the film tip over temperature (dotted line) and the linear fit obtained (black trace).

Extended Data Fig. 5 Modeling of the temperature dynamics.

Temperature of the LCN film upon switching the LED on (left) and off (right). The experimental data are the red traces and the calculated fits are the black traces.

Extended Data Fig. 6 Comparison of the experimental and calculated oscillations.

Experimental (green trace) and simulation (magenta trace) results of the oscillation over time.

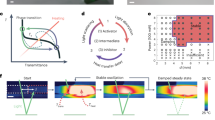
Extended Data Fig. 7 Modeling with a weak coupling showing changes in the final state depending on the starting conditions.

a, Example of non-periodic oscillations modeled with the coupling stiffness parameter kcoupling = 5 × 10−19 kg.m2.s−2 and the coupling damping parameter dcoupling. = 7.29 × 10−19 kg.m2.s−1, with the starting conditions \(\theta _1^0 = \theta _2^0\) = 2.3 rad showing instability and b, with the starting conditions \(\theta _1^0 = 2.6\,{\mathrm{rad}}\) and \(\theta _2^0 = 3.3\,{\mathrm{rad}}\) showing anti-phase oscillation.

Extended Data Fig. 8 Modeling with a weak coupling showing changes in the final state depending on the starting conditions.

a, Example of non-periodic oscillations modeled with the coupling stiffness parameter kcoupling = 5 × 10−19 kg.m2.s−2 and the coupling damping parameter dcouplin. = 7.29 × 10−19 kg.m2.s−1, with the starting conditions \(\theta _1^0 = 3.1\,{\mathrm{rad}}\) and \(\theta _2^0 = 2.3\,{\mathrm{rad}}\) showing non-periodic oscillations and b, with the starting conditions \(\theta _1^0 = 2.9\,{\mathrm{rad}}\) and \(\theta _2^0 = 2.6\,{\mathrm{rad}}\) showing in-phase oscillation.

Extended Data Fig. 9 Complex synchronized motion of coupled LCN experimentally obtained.

a, Displacement of the tips of the two coupled oscillators over time in the z-direction. The displacement of one oscillator is represented with the orange trace and the other one with the blue trace. b, A different motion obtained stochastically after switching the LED on and off. The data reported in graphs a and b are plotted from two different sequences combined in Supplementary Video 7. The data plotted on graph a are from the first minute of Supplementary Video 7, and the data on the graph b are from the second sequence of Supplementary Video 7.

Extended Data Fig. 10 Molecular structures.

Structures of the reactive mesogens RM82 and RM23, and structure of the chromophore Tinuvin 328.

Supplementary information

Supplementary Information

Supplementary Table 1 and captions for Supplementary Videos 1–7.

Supplementary Video 1

Photo-induced in-phase synchrony of the coupled oscillators. The video shows two thin films joined by the same material oscillating in-phase at a frequency of 8.5 Hz (Fig. 1c).

Supplementary Video 2

Photo-induced anti-phase synchrony of the coupled oscillators. The video shows two thin films joined by the same material oscillating in anti-phase at a frequency of 9.5 Hz (Fig. 1d).

Supplementary Video 3

Control experiments showing situations with no synchronization of the oscillation for two films. This video presents five successive video clips showing absence of synchrony between two strips with (1) the light beam focused exclusively on one of the two strips, (2) one of the two strips without LCN alignment, (3) no joint between the two independent strips, (4) the joint between the two strips clamped directly on the hinge with a rigid pair of tweezers and (5) a long joint of 10 mm between the two strips.

Supplementary Video 4

Photo-induced oscillation of a long strip of 18 mm length. The video shows a single strip of a length of 18 mm oscillating at a frequency of 5.5 Hz (Fig. 2c).

Supplementary Video 5

Photo-induced oscillation of a single short strip of 12 mm length. The video shows a single strip of a length of 12 mm oscillating at a frequency of 10.1 Hz (Fig. 2c).

Supplementary Video 6

Photo-induced in-phase oscillation of two asymmetric oscillators. The video shows joint strips of 12 mm and 18 mm oscillating at a frequency of 6.2 Hz. Although these two oscillators have different lengths and oscillate independently at different frequencies (Videos 4 and 5), they show here in-phase oscillation at the same frequency. This video demonstrates entrainment between asymmetric oscillators (Fig. 2d).

Supplementary Video 7

Complex motion of the coupled oscillators. This video shows the occasional complex motion observed and as plotted in Extended Data Fig. 9.

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vantomme, G., Elands, L.C.M., Gelebart, A.H. et al. Coupled liquid crystalline oscillators in Huygens’ synchrony. Nat. Mater. 20, 1702–1706 (2021). https://doi.org/10.1038/s41563-021-00931-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41563-021-00931-6

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing