Abstract
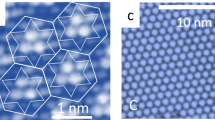
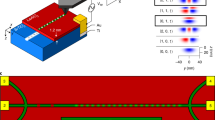
Distinct many-body states may be created under non-equilibrium conditions through different ordering paths, even when their constituents are subjected to the same fundamental interactions. The phase-transition mechanism to such states remains poorly understood. Here, we show that controlled optical or electromagnetic perturbations can lead to an amorphous metastable state of strongly correlated electrons in a quasi-two-dimensional dichalcogenide. Scanning tunnelling microscopy reveals a hyperuniform pattern of localized charges, whereas multitip surface nanoscale conductivity measurements and tunnelling spectroscopy show an electronically gapless conducting state that is different from conventional Coulomb glasses and many-body localized systems. The state is stable up to room temperature and shows no signs of either local charge order or phase separation. The mechanism for its formation is attributed to a dynamical localization of electrons through mutual interactions. Theoretical calculations confirm the correlations between localized charges to be crucial for the state’s unusual stability.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
Code used for the Monte Carlo simulations is available from the corresponding author upon reasonable request.
References
Zurek, W. Cosmological experiments in superfluid helium? Nature 317, 505 (1985).
Cavalleri, A. et al. Femtosecond structural dynamics in VO2 during an ultrafast solid–solid phase transition. Phys. Rev. Lett. 87, 237401 (2001).
Nasu, K., Ping, H. & Mizouchi, H. Photoinduced structural phase transitions and their dynamics. J. Phys. Condens. Mat. 13, R693–R721 (2001).
Iwai, S. et al. Photoinduced melting of a stripe-type charge-order and metallic domain formation in a layered BEDT-TTF-based organic salt. Phys. Rev. Lett. 98, 097402 (2007).
Schmitt, F. et al. Transient electronic structure and melting of a charge density wave in TbTe3. Science 321, 1649–1652 (2008).
Yusupov, R. et al. Coherent dynamics of macroscopic electronic order through a symmetry breaking transition. Nat. Phys. 6, 681–684 (2010).
Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 6, 1181–1203 (1973).
Anderson, P. W. Through the glass lightly. Science 267, 1615–1616 (1995).
Mitrano, M. et al. Possible light-induced superconductivity in K3C60 at high temperature. Nature 530, 461–464 (2016).
Giannetti, C. et al. Ultrafast optical spectroscopy of strongly correlated materials and high-temperature superconductors: a non-equilibrium approach. Adv. Phys. 65, 58–238 (2016).
Koshihara, S. et al. Photoinduced valence instability in the organic molecular compound tetrathiafulvalene-p-chloranil (TTF-CA). Phys. Rev. B 42, 6853–6856 (1990).
Fausti, D. et al. Light-induced superconductivity in a stripe-ordered cuprate. Science 331, 189–191 (2011).
Stojchevska, L. et al. Ultrafast switching to a stable hidden quantum state in an electronic crystal. Science 344, 177–180 (2014).
Zhang, J. et al. Cooperative photoinduced metastable phase control in strained manganite films. Nat. Mater. 15, 956–960 (2016).
Basov, D. N., Averitt, R. D. & Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 16, 1077–1088 (2017).
Gerasimenko, Y. A., Karpov, P., Vaskivskyi, I., Brazovskii, S. & Mihailovic, D. Intertwined chiral charge orders and topological stabilization of the light-induced state of a prototypical transition metal dichalcogenide. npj Quantum Mater. 4, 32 (2019).
Ravnik, J., Vaskivskyi, I., Mertelj, T. & Mihailović, D. Real-time observation of the coherent transition to a metastable emergent state in 1T-TaS2. Phys. Rev. B 97, 075304 (2018).
Nakanishi, K. & Shiba, H. Domain-like incommensurate charge-density-wave states and the first-order incommensurate–commensurate transitions in layered tantalum dichalcogenides. I. 1T-polytype. J. Phys. Soc. Jpn 43, 1839 (1977).
Tosatti, E. & Fazekas, P. On the nature of the low-temperature phase of 1T-TaS2. J. Phys. Colloques 37, C4-165–168 (1976).
Rossnagel, K. On the origin of charge-density waves in select layered transition-metal dichalcogenides. J. Phys. Condens. Mat. 23, 213001 (2011).
Ritschel, R. et al. Orbital textures and charge density waves in transition metal dichalcogenides. Nat. Phys. 11, 328–331 (2015).
Sipos, B. et al. From Mott state to superconductivity in 1T-TaS2. Nat. Mater. 7, 960–965 (2008).
Klanjsek, M. et al. A high-temperature quantum spin liquid with polaron spins. Nat. Phys. 13, 1130–1134 (2017).
Han, T.-R. T. et al. Exploration of metastability and hidden phases in correlated electron crystals visualized by femtosecond optical doping and electron crystallography. Sci. Adv. 1, e1400173 (2015).
Torquato, S. & Stillinger, F. H. Local density fluctuations, hyperuniformity, and order metrics. Phys. Rev. E 68, 411131–4111325 (2003).
Torquato, S. Hyperuniformity and its generalizations. Phys. Rev. E 94, 022122 (2016).
Ma, Z. & Torquato, S. Random scalar fields and hyperuniformity. J. Appl. Phys. 121, 244904 (2016).
Lesanovsky, Y. & Garrahan, J. P. Out-of-equilibrium structures in strongly interacting Rydberg gases with dissipation. Phys. Rev. A 90, 011603 (2014).
Jiao, Y. et al. Avian photoreceptor patterns represent a disordered hyperuniform solution to a multiscale packing problem. Phys. Rev. E 89, 022721 (2014).
Getzin, S. et al. Discovery of fairy circles in Australia supports self-organization theory. Proc. Natl Acad. Sci. USA 113, 3551–3556 (2016).
Torquato, S., Scardicchio, A. & Zachary, C. E. Point processes in arbitrary dimension from fermionic gases, random matrix theory, and number theory. J. Stat. Mech. Theory Exp. 2008, P11019 (2008).
Karpov, P. & Brazovskii, S. Modeling of networks and globules of charged domain walls observed in pump and pulse induced states. Sci. Rep. 8, 4043 (2018).
Dean, N. et al. Polaronic conductivity in the photoinduced phase of 1T-TaS2. Phys. Rev. Lett. 106, 016401 (2011).
Havlin, S. & Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 51, 187 (2002).
Burov, S., Metzler, R. & Barkai, E. Aging and nonergodicity beyond the Khinchin theorem. Proc. Natl Acad. Sci. USA 107, 13228 (2010).
Shklovskii, B. I. & Efros, A. L. Electronic Properties of Doped Semiconductors Vol. 45 (Springer, 1984).
Wang, Z. et al. Disorder induced power-law gaps in an insulator–metal Mott transition. Proc. Natl Acad. Sci. USA 115, 11198–11202 (2018).
Hellmann, S. et al. Time-domain classification of charge-density-wave insulators. Nat. Comms. 3, 1069 (2012).
Cho, D. et al. Nanoscale manipulation of the Mott insulating state coupled to charge order in 1T-TaS2. Nat. Comms. 7, 10956 (2016).
Ma, L. et al. A metallic mosaic phase and the origin of Mott-insulating state in 1T-TaS2. Nat. Commun. 7, 10453 (2016).
Svetin, D., Vaskivskyi, I., Brazovskii, S. & Mihailovic, D. Three-dimensional resistivity switching between correlated electronic states in 1T-TaS2. Sci. Rep. 7, 46048 (2017).
Mishima, O., Calvert, L. D. & Whalley, E. ‘Melting ice I’ at 77 K and 10 kbar: a new method of making amorphous solids. Nature 310, 393–395 (1984).
Miroshnichenko, A. E., Flach, S. & Kivshar, Y. S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 82, 2257–2298 (2010).
De Roeck, W. & Imbrie, J. Z. Many-body localization: stability and instability. Phil. Trans. R. Soc. A 375, 20160422 (2017).
Mahmoudian, S., Rademaker, L., Ralko, A., Fratini, S. & Dobrosavljević, V. Glassy dynamics in geometrically frustrated Coulomb liquids without disorder. Phys. Rev. Lett. 115, 025701 (2015).
Smith, A., Knolle, J., Kovrizhin, D. L. & Moessner, R. Disorder-free localization. Phys. Rev. Lett. 118, 266601 (2017).
Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Ann. Rev. Cond. Mat. Phys. 6, 15–38 (2015).
Rademaker, L., Pramudya, Y., Zaanen, J. & Dobrosavljević, V. Influence of long-range interactions on charge ordering phenomena on a square lattice. Phys. Rev. E 88, 032121 (2013).
Hanaguri, T. et al. A ‘checkerboard’ electronic crystal state in lightly hole-doped Ca2−xNaxCuO2Cl2. Nature 430, 1001–1005 (2004).
Schmalian, J. & Wolynes, P. Stripe glasses: self-generated randomness in a uniformly frustrated system. Phys. Rev. Lett. 85, 836–839 (2000).
Metropolis, N. et al. Equation of state calculations by fast computing machines. J. Chem. Phys. 21, 1087 (1953).
Mertelj, T., Kabanov, V. V. & Mihailović, D. Charged particles on a two-dimensional lattice subject to anisotropic Jahn–Teller interactions. Phys. Rev. Lett. 94, 147003 (2005).
Hukushima, K. & Nemoto, K. Exchange Monte Carlo method and application to spin glass simulations. J. Phys. Soc. Jpn 65, 1604–1608 (1996).
Acknowledgements
We thank T. Prosen, J. Bonča, P. Prelovšek, R. Žitko, T. Mertelj, S. Brazovskii, V. Dobrosavljevic, N. Gedik and P. Karpov for useful discussions, J. Mravlje for band structure data and P. Sutar for the synthesis and characterization of the samples. Funding from ERC-2012-ADG-20120216 ‘Trajectory’ is acknowledged.
Author information
Authors and Affiliations
Contributions
I.V. made the original discovery, and D.M. and Y.A.G. led the project, wrote the paper and performed the analysis. Y.A.G., M.L. and I.V. performed STM measurements, Y.A.G., M.D. and J.R. did the multitip measurements. J.V. and V.K. performed theoretical calculations. All the authors contributed to the Supplementary Information.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes 1–8, Supplementary Figs. 1–18 and Supplementary Refs. 1–29.
Rights and permissions
About this article
Cite this article
Gerasimenko, Y.A., Vaskivskyi, I., Litskevich, M. et al. Quantum jamming transition to a correlated electron glass in 1T-TaS2. Nat. Mater. 18, 1078–1083 (2019). https://doi.org/10.1038/s41563-019-0423-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-019-0423-3
This article is cited by
-
A high-efficiency programmable modulator for extreme ultraviolet light with nanometre feature size based on an electronic phase transition
Nature Photonics (2024)
-
Atomic-scale manipulation of single-polaron in a two-dimensional semiconductor
Nature Communications (2023)
-
In operando cryo-STEM of pulse-induced charge density wave switching in TaS2
Nature Communications (2023)
-
Chiral domain dynamics and transient interferences of mirrored superlattices in nonequilibrium electronic crystals
Scientific Reports (2023)
-
Scanning tunneling microscopy study of hidden phases in atomically thin 1T-TaS\(_2\)
Journal of the Korean Physical Society (2023)