Abstract
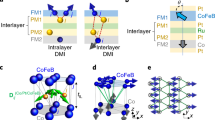
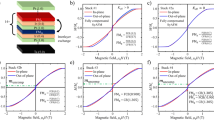
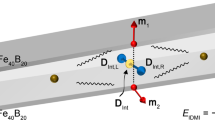
The exchange interaction governs static and dynamic magnetism. This fundamental interaction comes in two flavours—symmetric and antisymmetric. The symmetric interaction leads to ferro- and antiferromagnetism, and the antisymmetric interaction has attracted significant interest owing to its major role in promoting topologically non-trivial spin textures that promise fast, energy-efficient devices. So far, the antisymmetric exchange interaction has been found to be rather short ranged and limited to a single magnetic layer. Here we report a long-range antisymmetric interlayer exchange interaction in perpendicularly magnetized synthetic antiferromagnets with parallel and antiparallel magnetization alignments. Asymmetric hysteresis loops under an in-plane field reveal a unidirectional and chiral nature of this interaction, which results in canted magnetic structures. We explain our results by considering spin–orbit coupling combined with reduced symmetry in multilayers. Our discovery of a long-range chiral interaction provides an additional handle to engineer magnetic structures and could enable three-dimensional topological structures.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data sets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Change history
25 June 2019
In the version of this Article originally published, the sentence ‘D.-S.H. wrote the paper with K.L., J.H. and M.K.’ in the author contributions was incorrect; it should have read ‘D.-S.H. wrote the paper with K.L., J.H., M.-H.J. and M.K.’ This has been corrected in the online versions of the Article.
References
Dzyaloshinsky, I. A thermodynamic theory of ‘weak’ ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 241–255 (1958).
Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 120, 91–98 (1960).
Fert, A. & Levy, P. M. Role of anisotropic exchange interactions in determining the properties of spin-glasses. Phys. Rev. Lett. 44, 1538–1541 (1980).
Kundu, A. & Zhang, S. Dzyaloshinskii–Moriya interaction mediated by spin-polarized band with Rashba spin–orbit coupling. Phys. Rev. B 92, 94434 (2015).
Imamura, H., Bruno, P. & Utsumi, Y. Twisted exchange interaction between localized spins in presence of Rashba spin–orbit coupling. AIP Conf. Proc. 772, 1409–1410 (2005).
Bode, M. et al. Chiral magnetic order at surfaces driven by inversion asymmetry. Nature 447, 190–193 (2007).
Emori, S., Bauer, U., Ahn, S.-M., Martinez, E. & Beach, G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–616 (2013).
Miron, I. M. et al. Fast current-induced domain-wall motion controlled by the Rashba effect. Nat. Mater. 10, 419–423 (2011).
Ryu, K.-S., Thomas, L., Yang, S.-H. & Parkin, S. Chiral spin torque at magnetic domain walls. Nat. Nanotechnol. 8, 527–533 (2013).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Yu, X. Z. et al. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 3, 988 (2012).
Woo, S. et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 15, 501–506 (2016).
Litzius, K. et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nat. Phys. 13, 170–175 (2016).
Moreau-Luchaire, C. et al. Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nat. Nanotechnol. 11, 444–448 (2016).
Kim, S. et al. Correlation of the Dzyaloshinskii–Moriya interaction with Heisenberg exchange and orbital asphericity. Nat. Commun. 9, 1648 (2018).
Yu, X. Z. et al. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 9, 1648 (2018).
Yang, S.-H., Ryu, K.-S. & Parkin, S. Domain-wall velocities of up to 750 m s−1 driven by exchange-coupling torque in synthetic antiferromagnets. Nat. Nanotechnol. 10, 221–226 (2015).
Kim, K.-J. et al. Fast domain wall motion in the vicinity of the angular momentum compensation temperature of ferrimagnets. Nat. Mater. 16, 1187–1192 (2017).
Duine, R. A., Lee, K.-J., Parkin, S. S. P. & Stiles, M. D. Synthetic antiferromagnetic spintronics. Nat. Phys. 14, 217–219 (2018).
Jungwirth, T. et al. The multiple directions of antiferromagnetic spintronics. Nat. Phys. 14, 200–203 (2018).
Lavrijsen, R. et al. Magnetic ratchet for three-dimensional spintronic memory and logic. Nature 493, 647–650 (2013).
Fernández-Pacheco, A. et al. Three-dimensional nanomagnetism. Nat. Commun. 8, 15756 (2017).
Yang, Q. et al. Ionic liquid gating control of RKKY interaction in FeCoB/Ru/FeCoB and (Pt/Co)2/Ru/(Co/Pt)2 multilayers. Nat. Commun. 9, 991 (2018).
Xia, K., Zhang, W., Lu, M. & Zhai, H. Noncollinear interlayer exchange coupling caused by interface spin-orbit interaction. Phys. Rev. B 55, 12561–12565 (1997).
Vedmedenko, E. Y., Arregi, J. A., Riego, P. & Berger, A. Interlayer Dzyaloshinskii–Moriya interactions. Preprint at http://arXiv.org/cond-mat.mes-hall/:1803.10570 (2018).
Ummelen, F. C., Swagten, H. J. M. & Fernández-Pacheco, A. Canted States in Anti-ferromagnetically Coupled Magnetic Bilayers. Master’s thesis, Technische Universiteit Eindhoven (2013).
Je, S. G. et al. Asymmetric magnetic domain-wall motion by the Dzyaloshinskii–Moriya interaction. Phys. Rev. B 88, 214401 (2013).
Lo Conte, R. et al. Role of B diffusion in the interfacial Dzyaloshinskii–Moriya interaction in Ta/Co20Fe60B20/MgO nanowires. Phys. Rev. B 91, 14433 (2015).
Demokritov, S. O. Biquadratic interlayer coupling in layered magnetic systems. J. Phys. D 31, 925 (1998).
Pai, C.-F., Mann, M., Tan, A. J. & Beach, G. S. D. Determination of spin torque efficiencies in heterostructures with perpendicular magnetic anisotropy. Phys. Rev. B 93, 144409 (2016).
Han, D. S. et al. Asymmetric hysteresis for probing Dzyaloshinskii–Moriya interaction. Nano Lett. 16, 4438–4446 (2016).
Koplak, O. et al. Magnetization switching diagram of a perpendicular synthetic ferrimagnet CoFeB/Ta/CoFeB bilayer. J. Magn. Magn. Mater. 433, 91–97 (2017).
Lavrijsen, R. et al. Tuning the interlayer exchange coupling between single perpendicularly magnetized CoFeB layers. Appl. Phys. Lett. 100, 52411 (2012).
Barranco, A., Borras, A., Gonzalez-Elipe, A. R. & Palmero, A. Perspectives on oblique angle deposition of thin films: from fundamentals to devices. Prog. Mater. Sci. 76, 59–153 (2016).
Alvarez, R. et al. Nanostructured Ti thin films by magnetron sputtering at oblique angles. J. Phys. D 49, 045303 (2016).
Yu, G. et al. Switching of perpendicular magnetization by spin–orbit torques in the absence of external magnetic fields. Nat. Nanotechnol. 9, 548–554 (2014).
Khajetoorians, A. A. et al. Tailoring the chiral magnetic interaction between two individual atoms. Nat. Commun. 7, 10620 (2016).
Fernández-Pacheco, A. et al. Symmetry-breaking interlayer Dzyaloshinskii–Moriya interactions in synthetic antiferromagnets. Nat. Mater. https://doi.org/10.1038/s41563-019-0386-4 (2019).
Kurz, P., Förster, F., Nordström, L., Bihlmayer, G. & Blügel, S. Ab initio treatment of noncollinear magnets with the full-potential linearized augmented plane wave method. Phys. Rev. B 69, 24415 (2004).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Schweflinghaus, B., Zimmermann, B., Heide, M., Bihlmayer, G. & Blügel, S. Role of Dzyaloshinskii–Moriya interaction for magnetism in transition-metal chains at Pt step edges. Phys. Rev. B 94, 24403 (2016).
Acknowledgements
We acknowledge insightful discussions with M. Hoffmann, S. Blügel, B. Dupé and S.-B. Choe. We acknowledge F. Ummelen for personal discussions on her results that are relevant to this work. D.-S.H., K.L. and M.K. acknowledge support from MaHoJeRo (DAAD Spintronics network, project number 57334897) and the German Research Foundation (in particular SFB TRR 173 Spin+X). K.L. acknowledges the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement Standard EF no. 709151. M.-H.J. acknowledges support from the National Research Foundation (NRF) of Korea grant funded by the Korea government (MEST) (nos 2017R1A2B3007918 and 2016M3A7B4910400). C.-Y.Y. acknowledges support from the NRF of South Korea under Grant 2017R1A2B3002621 and 2015M3D1A1070465, and J.-P.H. and Y.M. acknowledge computing time on the supercomputers JUQUEEN and JURECA at the Jülich Super-computing Center, and at the JARA-HPC cluster of RWTH Aachen, as well as funding under the SPP 2137 “Skyrmionics” (project MO 1731/7-1) and project MO 1731/5-1 of the Deutsche Forschungsgemeinschaft (DFG). D.-S.H. and K.-W.K. were supported by the Korea Institute of Science and Technology (KIST) institutional program (no. 2E29410) and a National Research Council of Science & Technology (NST) grant (no. CAP-16-01-KIST) funded by the Korea government (Ministry of Science and ICT). K.-W.K. acknowledges the DFG (no. SI 1720/2-1).
Author information
Authors and Affiliations
Contributions
M.-H.J. and D.-S.H. conceived the original idea. D.-S.H., K.L., M.-H.J. and M.K. planned and designed the experiments. D.-S.H. and Y.V.H. fabricated the samples with R.L. and H.J.M.S. D.-S.H. and K.L. performed transport measurements with W.Y. and data analysis under the supervision of M.K. and M.-H.J. T.-W.K. provided [Pt/CoSiB]2/Pt multilayers. J.-P.H. and Y.M. performed the first-principles calculations and the analysis of relevant data. K.-W.K. provided theoretical explanations in Supplementary Information. D.-S.H. and C.-Y.Y. performed the numerical calculation based on a macrospin model. D.-S.H. wrote the paper with K.L., J.H., M.-H.J. and M.K. All the authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes 1–5, Supplementary Figs. 1–9 and Supplementary references 1–13.
Rights and permissions
About this article
Cite this article
Han, DS., Lee, K., Hanke, JP. et al. Long-range chiral exchange interaction in synthetic antiferromagnets. Nat. Mater. 18, 703–708 (2019). https://doi.org/10.1038/s41563-019-0370-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-019-0370-z
This article is cited by
-
Asymmetric magnetization switching and programmable complete Boolean logic enabled by long-range intralayer Dzyaloshinskii-Moriya interaction
Nature Communications (2024)
-
Field-free spin-orbit switching of perpendicular magnetization enabled by dislocation-induced in-plane symmetry breaking
Nature Communications (2023)
-
First-principles calculations for Dzyaloshinskii–Moriya interaction
Nature Reviews Physics (2022)
-
Orthogonal interlayer coupling in an all-antiferromagnetic junction
Nature Communications (2022)
-
Spin-orbit torque switching of chiral magnetization across a synthetic antiferromagnet
Communications Physics (2021)