Abstract
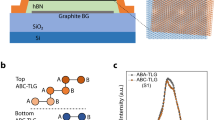
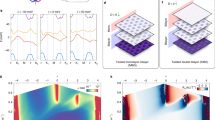
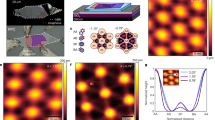
Control of the interlayer twist angle in two-dimensional van der Waals (vdW) heterostructures enables one to engineer a quasiperiodic moiré superlattice of tunable length scale1,2,3,4,5,6,7,8. In twisted bilayer graphene, the simple moiré superlattice band description suggests that the electronic bandwidth can be tuned to be comparable to the vdW interlayer interaction at a ‘magic angle’9, exhibiting strongly correlated behaviour. However, the vdW interlayer interaction can also cause significant structural reconstruction at the interface by favouring interlayer commensurability, which competes with the intralayer lattice distortion10,11,12,13,14,15,16. Here we report atomic-scale reconstruction in twisted bilayer graphene and its effect on the electronic structure. We find a gradual transition from an incommensurate moiré structure to an array of commensurate domains with soliton boundaries as we decrease the twist angle across the characteristic crossover angle, θc ≈ 1°. In the solitonic regime (θ < θc) where the atomic and electronic reconstruction become significant, a simple moiré band description breaks down and the secondary Dirac bands appear. On applying a transverse electric field, we observe electronic transport along the network of one-dimensional topological channels that surround the alternating triangular gapped domains. Atomic and electronic reconstruction at the vdW interface provide a new pathway to engineer the system with continuous tunability.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Li, G. et al. Observation of Van Hove singularities in twisted graphene layers. Nat. Phys. 6, 109–113 (2010).
Ponomarenko, L. et al. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013).
Dean, C. R. et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598–602 (2013).
Hunt, B. et al. Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructure. Science 340, 1427–1430 (2013).
Cao, Y. et al. Superlattice-induced insulating states and valley-protected orbits in twisted bilayer graphene. Phys. Rev. Lett. 117, 116804 (2016).
Kim, K. et al. Tunable moiré bands and strong correlations in small-twist-angle bilayer graphene. Proc. Natl Acad. Sci. USA 114, 3364–3369 (2017).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Woods, C. et al. Commensurate–incommensurate transition in graphene on hexagonal boron nitride. Nat. Phys. 10, 451–456 (2014).
Kim, N. Y. et al. Evidence of local commensurate state with lattice match of graphene on hexagonal boron nitride. ACS Nano 11, 7084–7090 (2017).
Van Wijk, M., Schuring, A., Katsnelson, M. & Fasolino, A. Relaxation of moiré patterns for slightly misaligned identical lattices: graphene on graphite. 2D Materials 2, 034010 (2015).
Dai, S., Xiang, Y. & Srolovitz, D. J. Twisted bilayer graphene: moiré with a twist. Nano Lett. 16, 5923–5927 (2016).
Nam, N. N. T. & Koshino, M. Lattice relaxation and energy band modulation in twisted bilayer graphene. Phys. Rev. B 96, 075311 (2017).
Gargiulo, F. & Yazyev, O. V. Structural and electronic transformation in low-angle twisted bilayer graphene. 2D Materials 5, 015019 (2018).
Zhang, K. & Tadmor, E. B. Structural and electron diffraction scaling of twisted graphene bilayers. J. Mech. Phys. Solids 112, 225–238 (2018).
Koma, A. Van der Waals epitaxy—a new epitaxial growth method for a highly lattice-mismatched system. Thin Solid Films 216, 72–76 (1992).
Alden, J. S. et al. Strain solitons and topological defects in bilayer graphene. Proc. Natl Acad. Sci. USA 110, 11256–11260 (2013).
Lin, J. et al. AC/AB stacking boundaries in bilayer graphene. Nano Lett. 13, 3262–3268 (2013).
Butz, B. et al. Dislocations in bilayer graphene. Nature 505, 533–537 (2014).
Yuk, J. M. et al. Superstructural defects and superlattice domains in stacked graphene. Carbon 80, 755–761 (2014).
Zhang, F., MacDonald, A. H. & Mele, E. J. Valley Chern numbers and boundary modes in gapped bilayer graphene. Proc. Natl Acad. Sci. USA 110, 10546–10551 (2013).
Vaezi, A., Liang, Y., Ngai, D. H., Yang, L. & Kim, E.-A. Topological edge states at a tilt boundary in gated multilayer graphene. Phys. Rev. X 3, 021018 (2013).
Ju, L. et al. Topological valley transport at bilayer graphene domain walls. Nature 520, 650–655 (2015).
Huang, S. et al. Topologically protected helical states in minimally twisted bilayer graphene. Phys. Rev. Lett. 121, 037702 (2018).
San-Jose, P. & Prada, E. Helical networks in twisted bilayer graphene under interlayer bias. Phys. Rev. B 88, 121408 (2013).
Anđelković, M., Covaci, L. & Peeters, F. M. DC conductivity of twisted bilayer graphene: Angle-dependent transport properties and effects of disorder. Phys. Rev. Mater. 2, 034004 (2018).
Li, J. et al. Gate-controlled topological conducting channels in bilayer graphene. Nat. Nanotechnol. 11, 1060–1065 (2016).
Rickhaus, P. et al. Transport through a network of topological channels in twisted bilayer graphene. Nano Lett. 18, 6725–6730 (2018).
McCann, E. Asymmetry gap in the electronic band structure of bilayer graphene. Phys. Rev. B 74, 161403 (2006).
Castro, E. V. et al. Biased bilayer graphene: semiconductor with a gap tunable by the electric field effect. Phys. Rev. Lett. 99, 216802 (2007).
Oostinga, J. B., Heersche, H. B., Liu, X., Morpurgo, A. F. & Vandersypen, L. M. Gate-induced insulating state in bilayer graphene devices. Nat. Mater. 7, 151–157 (2008).
Dos Santos, J. L., Peres, N. & Neto, A. C. Graphene bilayer with a twist: Electronic structure. Phys. Rev. Lett. 99, 256802 (2007).
Sanchez-Yamagishi, J. D. et al. Quantum Hall effect, screening, and layer-polarized insulating states in twisted bilayer graphene. Phys. Rev. Lett. 108, 076601 (2012).
Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).
Brown, L. et al. Twinning and twisting of tri- and bilayer graphene. Nano Lett. 12, 1609–1615 (2012).
Zhang, K. & Tadmor, E. B. Energy and moiré patterns in 2D bilayers in translation and rotation: A study using an efficient discrete-continuum interlayer potential. Extreme Mech. Lett. 14, 16–22 (2017).
Zhang, K. & Arroyo, M. Understanding and strain-engineering wrinkle networks in supported graphene through simulations. J. Mech. Phys. Solids 72, 61–74 (2014).
Zhang, K. & Arroyo, M. Coexistence of wrinkles and blisters in supported graphene. Extreme Mech. Lett. 14, 23–30 (2017).
Kolmogorov, A. N. & Crespi, V. H. Registry-dependent interlayer potential for graphitic systems. Phys. Rev. B 71, 235415 (2005).
Fang, S. & Kaxiras, E. Electronic structure theory of weakly interacting bilayers. Phys. Rev. B 93, 235153 (2016).
Carr, S., Fang, S., Jarillo-Herrero, P. & Kaxiras, E. Pressure dependence of the magic twist angle in graphene superlattices. Phys. Rev. B 98, 085144 (2018).
Massatt, D., Carr, S., Luskin, M. & Ortner, C. Incommensurate heterostructures in momentum space. Multiscale Model. Simul. 16, 429–451 (2018).
Lehmann, G. & Taut, M. On the numerical calculation of the density of states and related properties. Phys. Status Solidi b 54, 469–477 (1972).
Carr, S. et al. Relaxation and domain formation in incommensurate two-dimensional heterostructures. Phys. Rev. B 98, 224102 (2018).
Zhou, S., Han, J., Dai, S., Sun, J. & Srolovitz, D. J. van der Waals bilayer energetics: Generalized stacking-fault energy of graphene, boron nitride, and graphene/boron nitride bilayers. Phys. Rev. B 92, 155438 (2015).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Acknowledgements
We thank Y. Cao and P. Jarillo-Herrero for important discussions. The authors acknowledge the support of the Army Research Office (W911NF-14-1-0247) under the MURI programme. Part of the TEM analysis was supported by the Global Research Laboratory Program (2015K1A1A2033332) through the National Research Foundation of Korea (NRF). P.K. acknowledges partial support from the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant GBMF4543 and the Lloyd Foundation. R.E. acknowledges support from the National Science Foundation Graduate Research Fellowship under grant no. DGE1745303. P.C. acknowledges support from the National Science Foundation under grant no. DMS-1819220. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan and the CREST (JPMJCR15F3), JST. Nanofabrication was performed at the Center for Nanoscale Systems at Harvard, supported in part by NSF NNIN award ECS-00335765.
Author information
Authors and Affiliations
Contributions
H.Y. and P.K. conceived the experiments. H.Y. and R.E. performed the experiments and analysed the data. S.C., S.F. and E.K. performed the density functional theory calculation. K.Z. and E.B.T. conceived and performed the theoretical and FEM analyses. P.C. and M.L. performed mathematical modelling analysis. S.H.S., R.H., A.W.T., G.-C.Y. and M.K. performed TEM data analysis. K.W. and T.T. provided bulk hBN crystals. H.Y., R.E. and P.K. wrote the manuscript. All authors contributed to the overall scientific interpretation and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures 1–10, Supplementary References 1–19
Rights and permissions
About this article
Cite this article
Yoo, H., Engelke, R., Carr, S. et al. Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene. Nat. Mater. 18, 448–453 (2019). https://doi.org/10.1038/s41563-019-0346-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-019-0346-z
This article is cited by
-
Engineering interlayer hybridization in van der Waals bilayers
Nature Reviews Materials (2024)
-
One-dimensional proximity superconductivity in the quantum Hall regime
Nature (2024)
-
Local atomic stacking and symmetry in twisted graphene trilayers
Nature Materials (2024)
-
Evolution of the flat band and the role of lattice relaxations in twisted bilayer graphene
Nature Materials (2024)
-
Engineering interfacial polarization switching in van der Waals multilayers
Nature Nanotechnology (2024)