Abstract
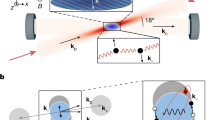
Controlling matter to simultaneously support coupled properties is of fundamental and technological importance1 (for example, in multiferroics2,3,4,5 or high-temperature superconductors6,7,8,9). However, determining the microscopic mechanisms responsible for the simultaneous presence of different orders is difficult, making it hard to predict material phenomenology10,11 or modify properties12,13,14,15,16. Here, using a quantum gas to engineer an adjustable interaction at the microscopic level, we demonstrate scenarios of competition, coexistence and mutual enhancement of two orders. For the enhancement scenario, the presence of one order lowers the critical point of the other. Our system is realized by a Bose–Einstein condensate that can undergo self-organization phase transitions in two optical resonators17, resulting in two distinct crystalline density orders. We characterize the coupling between these orders by measuring the composite order parameter and the elementary excitations and explain our results with a mean-field free-energy model derived from a microscopic Hamiltonian. Our system is ideally suited to explore quantum tricritical points18 and can be extended to study the interplay of spin and density orders19 as a function of temperature20.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Spaldin, N. A., Cheong, S.-W. & Ramesh, R. Multiferroics: Past, present, and future. Phys. Today 10, 38–43 (October, 2010).
Cheong, A.-W. & Mostovoy, M. Multiferroics: a magnetic twist for ferroelectricity. Nat. Mater. 6, 13–20 (2007).
Hur, N. et al. Electric polarization reversal and memory in a multiferroic material induced by magnetic fields. Nature 429, 392–395 (2004).
Lawes, G. et al. Magnetically driven ferroelectric order in Ni3V2O8. Phys. Rev. Lett. 95, 087205 (2005).
Heyer, O. et al. A new multiferroic material: MnWO4. J. Phys. Condens. Matter 18, L471–L475 (2006).
Tranquada, J. M., Sternlieb, B. J., Axe, J. D., Nakamura, Y. & Uchida, S. Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature 375, 561–563 (1995).
Carbotte, J. P., Schachinger, E. & Basov, D. N. Coupling strength of charge carriers to spin fluctuations in high-temperature superconductors. Nature 401, 354–356 (1999).
Daou, R. et al. Broken rotational symmetry in the pseudogap phase of a high-T c superconductor. Nature 463, 519–522 (2010).
Hinkov, V. et al. Electronic liquid crystal state in the high-temperature superconductor YBa2Cu3O6.45. Science 319, 597–600 (2008).
Demler, E., Hanke, W. & Zhang, S.-C. SO(5) theory of antiferromagnetism and superconductivity. Rev. Mod. Phys. 76, 909–974 (2004).
Artyukhin, S., Delaney, K. T., Spaldin, N. A. & Mostovoy, M. Landau theory of topological defects in multiferroic hexagonal manganites. Nat. Mater. 13, 42–49 (2014).
Norman, M. R., Randeria, M., Ding, H. & Campuzano, J. C. Phenomenology of the low-energy spectral function in high-T c superconductors. Phys. Rev. B 57, R11093(R) (1998).
Hill, N. A. Why are there so few magnetic ferroelectrics? J. Phys. Chem. B 104, 6694–6709 (2000).
Aschauer, U. & Spaldin, N. A. Competition and cooperation between antiferrodistortive and ferroelectric instabilities in the model perovskite SrTiO3. J. Phys. Condens. Matter 26, 122203 (2014).
Tsvelik, A. M. & Chubukov, A. V. Phenomenological theory of the underdoped phase of a high-T c superconductor. Phys. Rev. Lett. 98, 237001 (2007).
Nyéki, J. et al. Intertwined superfluid and density wave order in two-dimensional 4He. Nat. Phys. 13, 455–459 (2017).
Léonard, J., Morales, A., Zupancic, P., Esslinger, T. & Donner, T. Supersolid formation in a quantum gas breaking a continuous translational symmetry. Nature 543, 87–90 (2016).
Friedemann, S. et al. Quantum tricritical points in NbFe2. Nat. Phys. 14, 62–67 (2017).
Mivehvar, F., Piazza, F. & Ritsch, H. Disorder-driven density and spin self-ordering of a Bose–Einstein condensate in a cavity. Phys. Rev. Lett. 119, 063602 (2017).
Piazza, F., Strack, P. & Zwerger, W. Bose–Einstein condensation versus Dicke–Hepp–Lieb transition in an optical cavity. Ann. Phys. (NY) 339, 135–159 (2013).
Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, Cambridge, 1999).
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Colloquium: Theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).
Baumann, K., Guerlin, C., Brennecke, F. & Esslinger, T. Dicke quantum phase transition with a superfluid gas in an optical cavity. Nature 464, 1301–1306 (2010).
Baumann, K., Mottl, R., Brennecke, F. & Esslinger, T. Exploring symmetry breaking at the Dicke quantum phase transition. Phys. Rev. Lett. 107, 140402 (2011).
Ketterle, W., Durfee, D. S. & Stamper-Kurn, D. M. Making, Probing and Understanding BEC Course CXL (eds Inguscio, M. et al.) 67 (IOS, Amsterdam, 1999).
Léonard, J., Morales, A., Zupancic, P., Donner, T. & Esslinger, T. Monitoring and manipulating Higgs and Goldstone modes in a supersolid quantum gas. Science 358, 1415–1418 (2017).
Lang, J., Piazza, F. & Zwerger, W. Collective excitations and supersolid behavior of bosonic atoms inside two crossed optical cavities. New J. Phys. 19, 123027 (2017).
Bornholdt, S., Tetradis, N. & Wetterich, C. Coleman–Weinberg phase transition in two–scalar models. Phys. Rev. B 348, 89–99 (1995).
Gopalakrishnan, S., Shchadilova, Y. E. & Demler, E. Intertwined and vestigial order with ultracold atoms in multiple cavity modes. Phys. Rev. A 96, 063828 (2017).
Awadhesh, N., Balatsky, A. V. & Spaldin, N. A. Multiferroic quantum criticality. Preprint at https://arxiv.org/abs/1711.07989 (2017).
Acknowledgements
We thank E. Demler, S. Gopalakrishnan, A. Narayan, Y. E. Shchadilova and N. Spaldin for insightful discussions. We thank D. Dreon for careful reading of the manuscript and X. Li for experimental assistance. We acknowledge funding for the SBFI Horizon2020 project QUIC (grant agreement 641122) and the Horizon2020 European Training Network ColOpt (grant agreement 721465), and SNF support for the NCCR QSIT and the DACH project ‘Quantum Crystals of Matter and Light’.
Author information
Authors and Affiliations
Contributions
All authors contributed extensively to the work presented here.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures 1–3
Rights and permissions
About this article
Cite this article
Morales, A., Zupancic, P., Léonard, J. et al. Coupling two order parameters in a quantum gas. Nature Mater 17, 686–690 (2018). https://doi.org/10.1038/s41563-018-0118-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41563-018-0118-1
This article is cited by
-
Analysis of Shape Change of Droplet in Dipolar Bose–Hubbard Model
Journal of Low Temperature Physics (2022)
-
Multiferroic quantum criticality
Nature Materials (2019)