Abstract
Starting in mid-May 2020, many US states began relaxing social-distancing measures that were put in place to mitigate the spread of COVID-19. To evaluate the impact of relaxation of restrictions on COVID-19 dynamics and control, we developed a transmission dynamic model and calibrated it to US state-level COVID-19 cases and deaths. We used this model to evaluate the impact of social distancing, testing and contact tracing on the COVID-19 epidemic in each state. As of 22 July 2020, we found that only three states were on track to curtail their epidemic curve. Thirty-nine states and the District of Columbia may have to double their testing and/or tracing rates and/or rolling back reopening by 25%, while eight states require an even greater measure of combined testing, tracing and distancing. Increased testing and contact-tracing capacity is paramount for mitigating the recent large-scale increases in US cases and deaths.
Similar content being viewed by others
Main
The novel coronavirus pandemic (COVID-19), first detected in Wuhan, China in December 2019, has now reached pandemic status with spread to >210 countries and territories, including the United States1. The United States reported its first imported case of COVID-19 on 20 January 2020, arriving via an international flight from China2. Since then the disease has spread rapidly within the country, with every state reporting confirmed cases within 3 weeks of the first reported community transmission. As of 1 August, the United States has exceeded 4.5 million cases and 150,000 deaths, heterogeneously distributed across all states1. To date, states such as New York, New Jersey and California have borne the highest burden, with <420,000, 183,000 and 510,000 cases and 32,000, 15,000 and 9,000 deaths, respectively, while Alaska and Hawaii have each reported <4,000 cases and 25 deaths1.
COVID-19 is caused by a newly described and highly transmissible SARS-like coronavirus (SARS-CoV-2). Severe clinical outcomes have been observed in approximately 20% of symptomatic cases3,4. There is no vaccine and no cure or approved pharmaceutical intervention for this disease, making the fight against the pandemic reliant on non-pharmaceutical interventions (NPIs). These NPIs include: (1) case-driven measures such as testing, contact tracing and isolation5; (2) personal preventive measures such as hand hygiene, cough etiquette, face mask use, eye protection, physical distancing and surface cleaning, which aim to reduce the risk of transmission during contact with potentially infectious individuals6; and (3) social-distancing measures to reduce interpersonal contact in the population. In the United States, social-distancing measures have included policies and guidelines to close schools and workplaces, cancel and restrict mass gatherings and group events, restrict travel, maintain physical separation from others (for example, keeping six feet apart) and stay-at-home orders7.
Non-pharmaceutical interventions and other responses to COVID-19, especially stay-at-home orders, have varied widely across states, leading to spatial and temporal variation in the timing and implementation of mitigation strategies. This variation in policies and response efforts may have contributed to the observed heterogeneity in COVID-19 morbidity and mortality across states8. Recent studies suggest that state-wide social-distancing measures have probably contributed to reducing the spread COVID-19 epidemic in the United States9,10. Understanding the extent to which NPIs, such as social distancing, testing, contact tracing and self-quarantine, influence COVID-19 transmission in a local context is pivotal for predicting and better managing the future course of the epidemic on a state-by-state basis. This in turn will inform how these NPIs should be optimized to mitigate the spread and burden of COVID-19 while awaiting development of pharmaceutical interventions (for example, therapeutics and vaccines).
After several weeks of state-wide stay-at-home orders, most US states began to ease their social-distancing requirements in May/June 2020 (ref. 11) while attempting to increase their testing and contact-tracing capacities12. Mathematical modelling is a unique tool to help answer these important and timely questions. Models can contribute valuable insight for public health decision-makers by providing an evaluation of the effectiveness of ongoing control strategies along with predictions of the potential impact of alternative policy scenarios13.
To address these needs, we developed and validated a data-driven transmission dynamic model to evaluate the impact of social distancing, state reopening, testing and contact tracing on the state-level dynamics of COVID-19 infections and mortality in the United States, shown schematically in Fig. 1. Like many other COVID-19 transmission models14,15,16,17, we used an extended susceptible, exposed, infectious, removed (SEIR) compartmental model. The model divides the population into several disease compartments and tracks movements of individuals between the compartments through different transition rates. The main model compartments include: S, susceptible; E, exposed; A, infectious and asymptomatic; I, infectious and symptomatic; R, recovered; and F, dead. In addition to disease progression stages, our model incorporates social distancing informed by several public sources of mobility data, case identification via testing, isolation of detected cases and contact tracing. This is a mean-field epidemiological modelling approach that captures the average disease dynamics behaviour within a population18,19. We used Bayesian inference methods to calibrate and validate our model prediction to state-level daily reported COVID-19 cases and fatality data. Model parameters, prior distributions and their sources are shown in Table 1. We used the calibrated model to evaluate the transmissibility of COVID-19 in each state from March 2020 to late July 2020, to estimate the state-level impact of shelter-in-place and reopening on COVID-19 transmission. Finally, we evaluated the degree to which increasing testing efforts (rate of identification of infected cases) and/or contact tracing could curtail the spread of the disease and enable greater relaxation of social-distancing restrictions while preventing a resurgence of infections and deaths. A detailed description of the model considerations, parameterization and analysis is provided in Methods.
We used mobility data to constrain the time dependence of the contact rate. We fitted the model to daily reported cases and confirmed deaths from 19 March to 30 April 2020 and validated its projections against data from 1 May to 20 June 2020. On the model projections, the black solid line is the median, the pink band is the 95% CrI and the orange band is the IQR. We show model fitting and validation for four states: New York (NY), Ohio (OH), Texas (TX) and Washington (WA).
Results
Model performance and validation
We used state-level mobility data from Unacast, Google and OpenTable to calibrate a parametric model of shelter-in-place and reopening (Supplementary Fig. 1), and used the results to inform prior distributions for the transmission model (Fig. 1). We fit our model to state-level daily cases and deaths data using a Bayesian inference approach (Methods). Model performance assessment for several representative states is shown in Fig. 1, with full results in Supplementary Figs. 2 and 3. With respect to validation, the posterior 95% credible interval (CrI) of our model projections, estimated using data to 30 April 2020, covered 84% of the data points from 1 May to 20 June 2020. For seven states (Alaska, Montana, South Dakota, Iowa, Illinois, Michigan and Minnesota), validation had low coverage (<50%) because of insufficient training data to 30 April 2020 to adequately inform sheltering and reopening in those states. This inaccuracy was not unexpected, because the length of sheltering and the degree of reopening could not have been known on 30 April 2020, and thus our model predictions were based on generic prior distributions. However, during model calibration to data to 22 July 2020, these parameters were informed by updated state-specific mobility data. Model performance for fitting all data to 22 July 2020 is shown in Supplementary Figs. 4–6, with posterior parameter distributions shown in Supplementary Fig. 7. Good fits with high coverage (>88% for cases, >92% for deaths) were obtained for all states.
Estimations of effective reproduction number
The effective reproduction number, Reff, is the average number of secondary infection cases generated by a single infectious individual during their infectious period18. When Reff > 1 the epidemic curve is increasing, and when Reff < 1 the epidemic curve is decreasing18. Using the posterior distribution of our model parameters, we estimated Reff from 19 March to late July 2020 and identified the minimum level of transmission achieved in each state (Fig. 2a). We found that for all except five states (Alabama, Arkansas, North Carolina, Utah and Wisconsin), the interquartile range (IQR) for the minimum Reff value was <1 (varying 0.07–0.98), and these values were mainly achieved during the state shelter-in-place (11 April–29 May 2020) (Fig. 2a). Following states’ relaxations of social-distancing measures, disease transmission again started to increase. By 22 July 2020, 42 states and the District of Columbia had at least a 75% probability that Reff > 1. The model predicts therefore that, as states are reopening, a majority are at risk of continued increases in the scale of the outbreak and require additional mitigation to contain the spread of the disease.
a, Estimated Reff (median, IQR and 95% CrI) across states. The figure shows the value of Reff on 22 July 2020, as well as its minimum value between 19 March and 22 July 2020, in lighter shades of each colour. It also includes the date of minimum Reff. b, The level of reopening/rebound in disease transmission in each state relative to its minimum value during state shelter-in-place (median, IQR and 95% CrI).
We conducted an analysis of variance (ANOVA) to evaluate the contribution of each parameter to the variation in Reff (Supplementary Table 1). Across states, we found that the largest drivers of variation in Reff are (1) the power parameter for relating social distancing to hygiene-associated reduction in transmission, η (ANOVA F (one degree of freedom) = 2,989.166, P < 2.2 × 10–16, η2 > 5%, lower 95% confidence interval (CI) of η2 > 4.5%); (2) the degree of mitigation during shelter-in-place, θmin (ANOVA F (one degree of freedom) = 5,177.354, P < 2.2 × 10–16, η2 > 8.7%, lower 95% CI of η2 > 8.1%); (3) the maximum relative increase in contact after shelter-in-place orders, rmax (ANOVA F (one degree of freedom) = 8,051.61, P < 2.2 × 10–16, η2 > 13.5%, lower 95% CI of η2 > 12.8%); and (4) the fraction of contacts traced, fc (ANOVA F (one degree of freedom) = 13,834.053, P < 2.2 × 10–16, η2 > 23.2%, lower 95% CI of η2 > 22.4%), which together contribute >50% of variance (Extended Data Fig. 1 and Supplementary Table 1). This observation is consistent with mobility data alone being insufficient to account for the combined effect of multiple control measures, and suggests that the degree of adoption of non-mobility-related measures, such as enhanced hygiene practices and contact tracing, plays a large role in the extent to which a state may reduce disease transmission.
For each state, we defined Δ as the level of reopening/rebound (Δ = 0% at minimum, 100% at full reopening) in disease transmission relative to its lowest transmission rate observed during shelter-in-place, and estimated the current level of reopening/rebound (Fig. 2b). We found that 24 states had an average of 50–80% rebound in COVID-19 transmission by 22 July 2020, while no state had <25% rebound (Fig. 2b).
Impact of testing and contact tracing on easing of social distancing
Bringing and maintaining Reff < 1 is necessary to curtail the spread of an outbreak. We evaluated the probability of maintaining Reff < 1 for different levels of testing and contact tracing under the level of state reopening as of 22 July 2020. We found that in 42 states and the District of Columbia, bringing and maintaining Reff < 1 may not be possible without increased contact-tracing efforts because increasing testing and isolation alone would require at least a 3.5-fold increase in coverage to curtail the epidemic curve with 0.975 probability (Extended Data Figs. 2 and 3 and Supplementary Table 2). The challenges are even greater in ensuring continued control of the epidemic with full reopening, because testing and isolation alone would be insufficient to curtail the epidemic in 33 states and, in all states, contact-tracing coverage of 50–75% would be required to curtail the epidemic curve with 0.975 probability (Extended Data Fig. 4 and Supplementary Table 3).
To evaluate the impact of scaling up of testing and contact tracing on epidemic dynamics in each state, we assumed a linear ‘ramp-up’ of testing and/or contact tracing from 1–14 August 2020, after which both parameters remain constant. We then predicted the daily number of reported cases and deaths (Fig. 3 and Supplementary Fig. 8). We found that, under current levels of reopening and control, 40 states would be unable to curtail the spread of the epidemic within the following 2 months (Supplementary Fig. 8). Even with increased testing and contact tracing, these states will still experience an increase in reported cases and deaths of between 2 weeks and 2 months (Fig. 3 and Supplementary Fig. 8). For example, Ohio, Texas and Washington may experience a 2-week increase in cases and a 1-month increase in deaths even if their current testing and contact-tracing rates were doubled within the following 2 weeks (Fig. 3b–d). Moreover, reported cases increase during the 2-week ramp-up period (Fig. 3). We found that, in 27 states and the district of Columbia, an additional 25% (50%) relaxation of restrictions without simultaneously increasing contact tracing may exacerbate disease dynamics and result, on average, in increases of 25–65% (45–150%) in cases and 22–48% (35–92%) in deaths within the following 2 months (Supplementary Fig. 8).
We next evaluated the maximal degree of rebound in transmission (that is, level of reopening) permitted while maintaining Reff < 1 under different testing and contact-tracing scenarios (Fig. 4). We found that, under the current levels of testing and contact-tracing rate, 27 states cannot maintain Reff < 1 (at 75% confidence) even with only 25% reopening/rebound in transmission (Fig. 4a). By doubling the current testing rate, eight states could maintain Reff < 1 (at 75% confidence) even with a 50% level of reopening (Fig. 4b). By doubling contact tracing, nine states could remove all mobility restrictions while maintaining Reff < 1 (at 100% confidence) (Fig. 4c). By doubling both testing rate and contact tracing, ten states could remove all mobility restrictions while maintaining Reff < 1 (at 100% confidence) (Fig. 4d).
a–d, Levels of reopening/rebound if testing and contact rates are unchanged (a), testing rate is doubled (b), contact tracing is doubled (c) or both testing and contact tracing are doubled (d). Δ(t), the level of reopening/rebound in transmission on 22 July 2020, is denoted by circles. All boxplots show median, IQR and 95% CrI.
We categorized states by the additional amount of mitigation efforts needed to maintain R(t) < 1 with at least 75% confidence (Fig. 5 and Supplementary Fig. 8). We found that, under current control efforts, no states could reduce and maintain R(t) < 1 if their current level of reopening was relaxed by an additional 25% (‘Very Low’ category), and three states (Connecticut, Maine and New Hampshire) could reduce and maintain R(t) < 1 without additional reopening (‘Low’ category). Eight states could reduce and maintain R(t) < 1 by doubling their contact-tracing rate or by implementing additional social-distancing restrictions, a 25% reversal of the current level of reopening (‘Moderate’ category), while 30 states and the District of Columbia need a combined intervention of doubling both testing and contact tracing and/or 25% reversal of current reopening to reduce and maintain R(t) < 1 (‘High’ category). For the remaining eight states (Arizona, Florida, Idaho, Maryland, North Dakota, Nevada, South Carolina and Washington), a 50% reversal of current reopening, in addition to increased testing and/or contact tracing, are needed to reduce and maintain R(t) < 1 (‘Very High’ category).
Levels are based on maintaining R < 1 with at least 75% confidence, equivalent to the upper bound of IQR. Categories are based on evaluation of scenarios with different combinations of baseline/doubling testing, baseline/doubling contact tracing and baseline ±25% in the reopening parameter, Δ. Categories are defined as follows: Very Low (no states): can reopen further by >25% while maintaining R(t) < 1; Low (three states): can reopen further by <25% with up to 2× increase in testing while maintaining R(t) < 1; Moderate (nine states): requires 2× contact tracing or reversal of reopening by 25% to maintain R(t) < 1; High (30 states and DC): requires multiple interventions (2× testing, 2× contract tracing and reversal of reopening by 25%) to maintain R(t) < 1; Very High (eight states): reversal of reopening by 50% combined with 2× testing and/or 2× contact tracing to maintain R(t) < 1. Credit: the US map shapefile is derived from the usmap R package, which is open source under GPL-3.
Discussion
There is a delicate and continuous balance to strike between the use of social-distancing measures to mitigate the spread of an emerging and deadly disease such as COVID-19 and the need for reopening of various sectors of activities for the social, economic, mental and physical well-being of a community. To address this issue, it is imperative to design measurable, data-driven and flexible milestones to identify when to make specific transitions with regard to easing or re-tightening of specific social-distancing measures. We developed a data-driven SARS-CoV-2 transmission dynamic model, not only to make short-term predictions on COVID-19 incidence and mortality in the United States but, more importantly, to evaluate the impact of relaxation of social-distancing measures and increasing testing and contact tracing on the epidemic in each state.
We showed that, in most states, control strategies implemented during their shelter-in-place period were sufficient to contain the outbreak, defined as reducing and ultimately maintaining Reff < 1. However, for the majority of states, our modelling suggests that reopening has proceeded too rapidly and/or without adequate testing and contact tracing to prevent a resurgence of the epidemic. Our model suggests that, for some states, a substantial fraction of the population may have already been infected such that, even without additional intervention, Reff(t) is declining towards (or below) 1 even as R(t) > 1. The most extreme example is Arizona, where Reff(t) is estimated to have declined below the previous minimum Reff value achieved during shelter-in-place. However, accurate estimation of the susceptible fraction of the population is difficult due to the uncertain degree of undercounting in the reported case data. Thus, we used R(t) to categorize the mitigation requirements in each state and evaluate the level of control effort needed to curtail the spread of the epidemic in each state.
Moreover, even in states with currently decreasing incidence and mortality, such as Maine and New Jersey, additional relaxation of restrictions is likely to ‘bend the epidemic curve upwards’ in the absence of increased testing or tracing. However, our model predicts that a combination of increased testing, increased contact tracing and/or scaling back of reopening will be sufficient to curtail the spread of COVID-19 in most states. Specifically, doubling of current testing and contact-tracing rates would enable the majority of states to either maintain or increase the easing of social-distancing restrictions in a ‘safe’ manner in the short term. Scaling back the current level of reopening by 25%, in combination with doubling of testing and tracing, will be sufficient to control the epidemic in the long term in all but eight Very High risk states. The impact of these interventions on the epidemic curve was evaluated by computing their probability of reducing and maintaining R < 1. However, in states with high over-dispersion in disease transmission and faced with an epidemic with high super-spreadability characteristics, the reproduction number may be subject to large fluctuation as the number of infection cases decreases. This is more likely to be the case for states with lower dispersion parameters posterior values, such as Arkansas, Connecticut, Idaho, Kansas, Kentucky, Louisiana, Mississippi, New Hampshire, South Carolina and Wyoming (Supplementary Fig. 7).
Increasing testing and contact-tracing rates entails both increasing the number of tests performed per day and requires early identification and effective isolation of COVID-19-infected individuals. This can be accomplished through active case detection via efficient contact-tracing strategies. However, it should also be noted that increased testing and contact tracing will lead to a short-term increase in reported cases because a larger fraction of the infected population is being observed, and that several weeks may pass before these rates begin to show a decline. Therefore, it is imperative that policymakers and the public recognize that such a surge is actually a sign that testing and tracing efforts are succeeding, and exercise the patience to wait several weeks before these successes are reflected as declining rates of reported cases.
Other modelling studies have used SEIR-type compartmental models to assess the impact of social distancing, testing and contact tracing to curb the epidemic curve in Italy and the United Kingdom14,15,16,17. Consistent with our results, these studies have shown that rapid reopening of the economy without adequate testing and contact tracing could lead to a resurgence of the epidemic14,15,16,17. Specifically, they show that high testing and contact-tracing rates may enable the maintenance and increase the easing of social-distancing restrictions without an increased rate of COVID-19 transmission14.
Our study has several limitations, due to modelling assumptions and the quality of available data. Like most COVID-19 transmission models14,15,16,17, we used a compartmental SEIR-type model to model the spread of SARS-CoV-2 because of its simplicity and ability to capture population average dynamics. This modelling approach does not account for heterogeneity in individual-level behaviour, over-dispersion due to super-spreaders, social contact networks and inherent stochasticity, which may play an important role in SARS-CoV-2 transmission dynamics. Although these factors can be modelled through the use of individual-based models20,21,22, individual-based modelling is a more complex modelling framework and may require a substantial amount of individual-level data for model parameterization, calibration and validation.
To characterize the limitations of using cell-phone-based mobility data to infer (prior distributions for) contact rates, we examined the state-to-state variation in mobility data to the corresponding posterior distributions for each mobility-related parameter (Supplementary Fig. 9). Three parameters of particular interest are the minimum relative contact rate (θmin), the duration of the shelter-in-place phase (τs) and the maximum amount of reopening (rmax). For θmin, none of the r2 values were consistently <0.2 although the slope and intercept of the regression line for the Unacast Visitation metric were within 15% of 1 and 0, respectively. Similarly, for τs, the highest r2 value was 0.37 for OpenTable Bookings data, which also had a relatively accurate regression line (again within 15%). For rmax, the highest r2 values were for Google retail and recreation (0.49) and Unacast Visitation (0.52) metrics, but the Google data were much more accurate with a slope close to 1 and intercept close to 0. Overall, these results suggest that cell-phone-based mobility data vary substantially in their accuracy (slope and intercept near 1 and 0, respectively) and, overall, have low precision (no r2 more than about 0.5), and support our use of the range across multiple sources in developing prior distributions, rather than using such data directly for modelling contact rates.
The initiation of social-distancing measures, such as stay-at-home orders in the United States, for mitigating the spread of COVID-19 has occurred concurrently with increased promotion and application of other NPIs, such as hygiene practices (for example, hand hygiene, surface cleaning, cough etiquette and wearing of a face mask). These hygiene practices, coupled with the avoidance of physical contact whenever possible (keeping six feet apart), could impact the spread of COVID-19 by reducing the risk of both exposure and transmission of SARS-CoV-2 from infected patients23,24. Though our model explicitly accounts for the differential contribution of social distancing (mobility reduction) versus hygiene practices and physical distancing to reducing COVID-19 transmission, we assume that the impact of hygiene practices and physical distancing was a function of social distancing (mobility reduction). While mobile phone mobility data may continue to be informative in regard to to contact rates, at least in aggregate, the impact of enhanced hygiene practices is more difficult to measure independently. As several states have eased their social-distancing requirements, especially their stay-at-home orders, compliance with hygiene practices would become even more important for reducing individuals’ risk of getting or transmitting the pathogen. However, keeping a high population-level adherence to these measures is required to mitigate the spread of the COVID-19 epidemic25. As states are reopening various aspects of their economy, data on compliance with enhanced hygiene practices and physical distancing are needed to improve the estimation of these measures’ population-level impact on reducing disease transmission.
Additionally, consistent with previous COVID-19 modelling studies26,27,28, our model uses a simple functional form to model increases in testing rate from early March to June 2020. This testing rate was estimated through model fitting to daily reported case and mortality data. Particularly in states that have seen a substantial increase in testing capability and efforts during the month of May, our simple time-varying assumption may underestimate the current level of testing and contact tracing. However, it should be noted that increased testing capacity does not necessarily lead to an increased rate of testing if individuals are unaware, unwilling or unable to be tested29. Having data on contact tracing and date of symptoms onset would enable us to compute a better estimate of the current testing and contact-tracing rate in each state. Our model also assumes that all individuals who test positive to COVID-19 are effectively isolated for the remainder of their infectious period and no longer contribute to disease transmission. Though voluntary compliance to COVID-19 self-quarantine recommendations may be high across the United States, it is probably not 100%. Therefore, the assumption of effective isolation of all identified cases may cause our model to slightly overestimate the impact of increased testing rate on disease dynamics. However, we anticipate that this assumption would have only a marginal impact on the qualitative nature of our results.
Finally, our model does not explicitly account for age-stratified risk of disease transmission and mortality. This age stratification is important for the design and evaluation of social-distancing and testing strategies that are targeted towards the elderly population, which is at higher risk of COVID-19-induced hospitalization and death30. As reopening the economy becomes an imperative for states across the United States, age- or risk-targeted interventions may be a valuable tool to mitigate the burden of the pandemic. Future modelling studies could investigate the effectiveness of age- or risk-targeted non-pharmaceutical and potential pharmaceutical (vaccine or therapeutic) interventions for controlling the spread and burden of COVID-19.
In sum, we use a data-driven mathematical modelling approach to study the impacts of social distancing, testing and contact tracing on the transmission dynamics of SARS-CoV-2. Our findings emphasize the importance for public health authorities not only to monitor the case and mortality dynamics of SARS-CoV-2 in their state, but also to understand the impact of their existing social-distancing measures on SARS-CoV-2 transmission and to evaluate the effectiveness of their testing and contact-tracing programmes for prompt identification and isolation of new cases of COVID-19. As reported, case rates are increasing widely across US states because social-distancing restrictions have been eased to allow the resumption of greater economic activity, and we find that most states need to either substantially scale back reopening or enhance their capacity and scale of testing, case-isolation and contact-tracing programmes to mitigate large-scale increases in COVID-19 cases and deaths.
Methods
Our overall approach is as follows: (1) develop a mathematical model (an SEIR-type compartmental model)18,19 that incorporates social-distancing data, case identification via testing, isolation of detected cases and contact tracing; (2) assess the model’s predictive performance by training (calibrating) it to reported cases and mortality data from 19 March to 30 April 2020 and validating its predictions against data from 1 May to 20 June 2020; and (3) use the model, trained on data to 22 July 2020, to predict future incidence and mortality. The final stage of our approach predicts future events under a set of scenarios that include increased case detection through expansion of testing rate, contact tracing and relaxation or increase of measures to promote social distancing. All model fitting is performed in a Bayesian framework to incorporate available prior information and address multivariate uncertainty in model parameters.
Model formulation
We modified the standard SEIR model to address testing and contact tracing, as well as asymptomatic individuals. A fraction fA of those exposed (E) to enter the asymptomatic A class (divided into AU for untested and AC for contact traced) instead of the infected I class, which in our model formulation also includes infectious presymptomatic individuals. With respect to testing, separate compartments were added for untested, ‘freely roaming’ infected individuals (IU), tested/isolated cases (IT) and fatalities (FT). Following recovery, untested infected individuals (IU) and all asymptomatic individuals move to the untested recovered compartment, IU, and tested infected individuals move to the tested recovered compartment, IT. In balancing considerations of model fidelity and parameter identifiability, we made the reasonably conservative assumptions that all tested cases are effectively isolated (through self-quarantine or hospitalization) and thus unavailable for transmission, and that all COVID-related deaths are identified/tested.
With respect to contact tracing, the additional compartment SC represents unexposed contacts who undergo a period of isolation during which they are not susceptible before returning to S, while EC, AC and IC represent contacts who were exposed. Again, the reasonably conservative assumption was made that all exposed contacts undergo testing, with an accelerated testing rate compared to the general population. We assume a closed population of constant size, N, for each state.
The ordinary differential equations governing our model are as follows:
where c is the contact rate between individuals, β is the transmission probability per infected contact, fC is the fraction of contacts identified through contact tracing, 1/γ is the duration of self-isolation after contact tracing, 1/κ is the latent period, fA is the fraction of exposed who are asymptomatic, λ is the testing rate, δ is the fatality rate, ρ is the recovery rate and λC and ρC are the testing and recovery rates, respectively, of contact-traced individuals. The testing rates λ and λC, the fatality rate δ and the recovery rate of traced contacts ρC are each composites of several underlying parameters. The testing rate defined as
where Ftest,0 is the current testing coverage (fraction of infected individuals tested), Senstest is the test sensitivity (true positive rate) and ktest is the rate of testing for those tested, with a typical time-to-test equal to 1/ktest. The time-dependence term models the ramping up of testing using a logistic function with a growth rate of 1/τT d−1, where T50T is the time where 50% of the current testing rate is achieved. Similarly, for testing of traced contacts, the same definition is used with the assumption that all identified contacts are tested, Ftest,0 = 1 and at a faster assumed testing rate, kC,test:
Because all contacts are assumed to be tested, the rate ρC at which they enter the ‘recovered’ compartment, RU is simply the rate of false negative test results:
The fatality rate is adjusted to maintain consistency with the assumption that all COVID-19 deaths are identified, assuming constant IFR. Specifically, we first calculated the fraction of infected that is tested and positive:
Then the case fatality rate CFR(t) = IFR/fpos(t). Because CFR = δ/(δ + ρ), this implies
The model is ‘seeded’ Ninitial cases on 29 February 2020. Because in the early stages of the outbreak there may be multiple ‘imported’ cases, we fit to data only from 19 March 2020 onwards, 1 week after the US travel ban was put in place31.
Our model is fit to daily case yc and death yd data (cumulative data are not used for fitting because of autocorrelation). To adequately fit the case and mortality data, we accounted for two lag times. First, a lag is assumed between leaving the IU compartment and public reporting of a positive test result, accounting for the time it takes to seek a test, obtain testing and have the result reported. No lag is assumed for tests from contact tracing. Second, a lag time is assumed between entering the fatally ill compartment FT and publicly reported deaths. Additionally, we use a negative binomial likelihood to account for the substantial day-to-day over-dispersion in reporting results. The corresponding equations are as follows:
In this parameterization, because the dispersion parameter α → ∞, the likelihood becomes a Poisson distribution with expected value ypred,[c,d], whereas for small values of α there is substantial interindividual variability. Case and death data were sourced from The COVID Tracking Project32.
Finally, we derived the time-dependent reproduction number, R(t) and the effective reproduction number, Reff(t) of this model, given by
and
Reff(t) is the average number of secondary infection cases generated by a single infectious individual during their infectious period in partially susceptible population at time t. It is equal to the product of the transmission risk per contact of an infectious individual with their untraced contacts, c × β × (1 − fC), times their average duration of infection, \(\left( {\frac{{1 - f_{\mathrm{A}}}}{{\lambda + \rho }} + \frac{{f_{\mathrm{A}}}}{\rho }} \right)\), and the portion of contacts that are susceptible, \(\frac{{{{S}}(t)}}{N}\). This accounts for the relative contribution of asymptomatic, \(c \times \beta \times \left( {1 - f_{\mathrm{C}}} \right)\left( {\frac{{f_{\mathrm{A}}}}{\rho }} \right) \times \frac{{{{S}}(t)}}{N}\) and symptomatic infection, \(c \times \beta \times (1 - f_{\mathrm{C}})\left( {\frac{{1 - f_{\mathrm{A}}}}{{\lambda + \rho }}} \right) \times \frac{{{{S}}(t)}}{N}\). Using posterior samples for all 50 states and the District of Columbia, we conducted an analysis of variance using a linear model to characterize the contributions to the combined interstate and intrastate variation in Reff. Specifically, we used a linear model for Reff with the model parameters R0, η, θmin, rmax, fC, fA, λ and ρ as predictors, and evaluated the percentage of variance in Reff contributed by each parameter.
Incorporating social distancing, enhanced hygiene practices and reopening
The impact of social distancing, hygiene practices and reopening was modelled through a time dependence in the contact rate, c and the transmission probability per infected contact, β:
The θ(t) function parameterized social distancing during the progression to shelter-in-place, and is modelled as a Weibull function:
which starts as unity and decreases to θmin, with τθ being the Weibull scale parameter and nθ the Weibull shape parameter (Fig. 1).
The r(t) function parameterized relative increase in contacts due to reopening after shelter-in-place, with r = 1 corresponding to a return to baseline c = c0.
The term r(t) is 0 before tr, linear between tr and trmax and constant at a value of rmax after that, and made continuous by approximating the Heaviside function by a logistic function. The reopening time is defined as τs days after τθ, and the maximum relative increase in contacts rmax happens τr days after that.
We selected the functional form above for c(t) because it was found to be able to represent a wide variety of social-distancing data, including mobile phone mobility data from Unacast33 and Google34 as well as restaurant booking data from OpenTable35. We used these different mobility sources to derive state-specific prior distributions because different social-distancing datasets had different values for θmin, τθ, nθ, τs, rmax and τr (Supplementary Fig. 1).
With respect to the reduction in transmission probability β, we assumed that during the shelter-in-place phase, hygiene-based mitigation paralleled this decline with an effectiveness power η, and that this mitigation continued through reopening.
Finally, we define an overall reopening parameter Δ that measures the rebound in disease transmission, c × β relative to its minimum, defined to be 0 during shelter-in-place (that is, R(t) is at a minimum) and 1 when all restrictions are removed (when R(t) = R0), which can be derived as:
Our model is illustrated in Fig. 1, with parameters and prior distributions listed in Table 1.
Scenario evaluation
We used the model to make several inferences about the current and future course of the pandemic in each state. First, we consider the effective reproduction number. Two time points of particular interest are the time of minimum Reff, reflecting the degree to which shelter-in-place and other interventions were effective in reducing transmission, and the final time of the simulation, 22 July 2020, reflecting the extent to which reopening has increased Reff. Additional parameters of interest are the current levels of reopening Δ(t), testing λ and contact tracing fC.
We then conducted scenario-based prospective predictions using our model’s parameters as estimated to 22 July 2020. We then asked the following questions:
-
(1)
Assuming current levels of reopening, what increases in general testing λ and/or contact tracing fC would be necessary to bring Reff < 1?
-
(2)
What level of reopening Δ can maintain Reff < 1 under four different scenarios: current values of testing and contact tracing, doubling testing, double tracing and doubling both testing and tracing?
-
(3)
What will be the rates of new cases and deaths under different scenarios? Specifically, we evaluate the impact of increases in testing and contact tracing under current levels of reopening, as well as increases or decreases of 25 or 50%.
For (1), we evaluated the posterior probability that Reff < 1 under scaling transformations λ → λ × μλ and fC → fC × μC with scaling factors μλ and μC:
We additionally derived ‘critical’ values of μC and μλ where Reff(t) < 1 under the conditions of increased testing alone (μC = 1), increased contact tracing alone (μλ = 1) and equal increases in testing and tracing (μC = μλ). We also performed the same analysis under a full reopening scenario (that is, setting S(t) = 1, c = c0 and β = β0).
For (2), we rearranged the equation for Reff in terms of the reopening parameter Δ:
We then fixed the scaling factors at 1 or 2, and solved the above equation to determine the percentage of reopening (Δcrit) that can be achieved while keeping Reff < 1. Values of Δcrit ≥ Δ(t) indicate the additional degree of reopening possible while maintaining Reff < 1, while values of Δcrit < Δ(t) indicate that reduction of reopening is needed. To convert back to testing and contact-tracing rates, we multiplied the scaling factors μC and μλ by the original values of fC and λ, respectively.
Finally, for (3), we additionally evaluated changes in reopening Δ → Δ + ΔΔ for ΔΔ values of +25% (+50%) or −25% (−50%), for a total of 20 scenarios (four different levels of testing and tracing and five different levels of reopening). We then ran the SEIR model forward in time to 30 September 2020. For all three intervention parameters, μC, μλ and ΔΔ, we assumed a ramp-up period of 2 weeks from 1 to 14 August 2020.
To summarize the relative need for mitigation in each state, we categorized states based on which scenarios resulted in the IQR of R(t) < 1 on 15 August 2020. The categories were defined as follows:
-
Very Low: can reopen further by >25% while maintaining R(t) < 1
-
Low: can reopen further by <25% with up to 2× increase in testing while maintaining R(t) < 1
-
Moderate: requires 2× contact tracing or reversal of reopening by 25% to bring and maintain R(t) < 1
-
High: requires multiple interventions (2× testing, 2× contract tracing and reversal of reopening by 25%) to bring and maintain R(t) < 1
-
Very High: combining 2× testing, 2× contact tracing and reversal of reopening by 50% is needed to bring and maintain R(t) < 1
We use R(t) instead of Reff(t), to minimize the impact of heterogeneity and uncertainty in the value of S(t)/N on our results. Thus, requiring R(t) < 1 provides greater assurance of state-wide control of the epidemic.
Software and code
Posterior distributions were sampled with Markov chain Monte Carlo (MCMC) simulation performed using MCSim v.6.1.0 in Metropolis within Gibbs sampling36. For each US state, four chains of 200,000 iterations each were run, with the first 20% of runs discarded and 500 posterior samples saved for analysis. For each parameter, comparison of interchain and intrachain variability was assessed to determine convergence, with the potential scale reduction factor R ≤ 1.2 considered converged37. Additional analysis of model outputs was performed in RStudio v.1.2.1335 (ref. 38) with R v.3.6.1 (ref. 39).
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The following publicly available datasets are used: mobility data from Unacast were sourced from https://covid19-scoreboard-api.unacastapis.com/api/search/covidstateaggregates_v3; mobility data from Google were sourced from https://www.gstatic.com/covid19/mobility/Global_Mobility_Report.csv; restaurant booking data were sourced from OpenTable, https://www.opentable.com/state-of-industry; case and death data were sourced from The COVID Tracking Project, https://covidtracking.com/.
Mobility data are shown in Supplementary Fig. 1. Case and death data are shown in Figs. 1 and 3 and Supplementary Figs. 3–6 and 8. All data used are also available in the software and code repository.
Code availability
The codes used to generate our results will be available on GitHub prior to publication, at https://github.com/wachiuphd/COVID-19-Bayesian-SEIR-US.
References
Johns Hopkins Coronavirus Resource Center (Johns Hopkins University of Medicine, accessed 18 May 2020); https://coronavirus.jhu.edu/
Holshue, M. L. et al. First case of 2019 novel coronavirus in the united states. N. Engl. J. Med. 382, 929–936 (2020).
Weiss, P. & Murdoch, D. R. Clinical course and mortality risk of severe COVID-19. Lancet 395, 1014–1015 (2020).
Wu, Z. & McGoogan, J. M. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: summary of a report of 72314 cases from the Chinese Center for Disease Control and Prevention. JAMA 323, 1239–1242 (2020).
Kucharski, A. J. et al. Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: a mathematical modelling study. Lancet Infect. Dis. 20, 1151–1160 (2020).
Chu, D. K. et al. Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: a systematic review and meta-analysis. Lancet 395, 1973–1987 (2020).
Pearce, K. What is social distancing and how can it slow the spread of COVID-19? John Hopkins University Hub https://hub.jhu.edu/2020/03/13/what-is-social-distancing/ (2020).
Bialek, S. et al. Geographic differences in covid-19 cases, deaths, and Incidence—United States, February 12–April 7, 2020. Mmwr. Morb. Mortal. Wkly Rep. 69, 465–471 (2020).
Siedner, M. J. et al. Social distancing to slow the U.S. COVID-19 epidemic: an interrupted time-series analysis. PLoS Med. 17, e1003244 (2020).
Wagner, A. B. et al. Social distancing has merely stabilized COVID-19 in the US. Stat https://doi.org/10.1002/sta4.302 (2020).
Tolbert, J., Kates, J. & Levitt, L. Lifting social distancing measures in America: state actions & metrics. KFF.org https://www.kff.org/coronavirus-policy-watch/lifting-social-distancing-measures-in-america-state-actions-metrics/ (2020).
CDC COVID Data Tracker (Centers for Disease Control and Prevention, accessed 18 May 2020); https://www.cdc.gov/coronavirus/2019-ncov/cases-updates/testing-in-us.html
Garnett, G. P., Cousens, S., Hallett, T. B., Steketee, R. & Walker, N. Mathematical models in the evaluation of health programmes. Lancet 378, 515–525 (2011).
Giordano, G. et al. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 26, 855–860 (2020).
Russo, L. et al. Tracing DAY-ZERO and forecasting the fade out of the COVID-19 outbreak in Lombardy, Italy: a compartmental modelling and numerical optimization approach. Preprint at medRxiv https://doi.org/10.1101/2020.03.17.20037689 (2020).
Gevertz, J., Greene, J., Tapia, C. H. S. & Sontag, E. D. A novel COVID-19 epidemiological model with explicit susceptible and asymptomatic isolation compartments reveals unexpected consequences of timing social distancing. Preprint at medRxiv https://doi.org/10.1101/2020.05.11.20098335 (2020).
Colbourn, T. et al. Modelling the health and economic impacts of population-wide testing, contact tracing and isolation (PTTI) strategies for COVID-19 in the UK. Preprint at SSRN https://doi.org/10.2139/ssrn.3627273 (2020).
Anderson, R. M., May, R. M. & Anderson, B. Infectious Diseases of Humans: Dynamics and Control (Oxford Univ. Press, 1992).
Murray, J. D. Mathematical Biology I. An Introduction (Springer, 2002).
Moghadas, S. M. et al. The implications of silent transmission for the control of COVID-19 outbreaks. Proc. Natl Acad. Sci. USA 117, 17513–17515 (2020).
Chinazzi, M. et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 368, 395–400 (2020).
Panovska-Griffiths, J. et al. Determining the optimal strategy for reopening schools, the impact of test and trace interventions, and the risk of occurrence of a second COVID-19 epidemic wave in the UK: a modelling study. Lancet Child Adolesc. Health https://doi.org/10.1016/S2352-4642(20)30250-9 (2020).
Leung, N. H. L. et al. Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat. Med. 26, 676–680 (2020).
Greenhalgh, T., Schmid, M. B., Czypionka, T., Bassler, D. & Gruer, L. Face masks for the public during the covid-19 crisis. BMJ 369, m1435 (2020).
Eikenberry, S. E. et al. To mask or not to mask: modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infect. Dis. Model. 5, 293–308 (2020).
Pitzer, V. E. et al. The impact of changes in diagnostic testing practices on estimates of COVID-19 transmission in the United States. Preprint at medRxiv https://doi.org/10.1101/2020.04.20.20073338 (2020).
Yamana, T., Pei, S., Kandula, S. & Shaman, J. Projection of COVID-19 cases and deaths in the US as individual states re-open May 4, 2020. Preprint at medRxiv https://doi.org/10.1101/2020.05.04.20090670 (2020).
Peirlinck, M., Linka, K., Sahli Costabal, F. & Kuhl, E. Outbreak dynamics of COVID-19 in China and the United States. Biomech. Model. Mechanobiol. https://doi.org/10.1007/s10237-020-01332-5 (2020).
Thompson, S., Eilperin, J. & Dennis, B. U.S. states see COVID-19 testing supply improvements, but challenges abound. The Washington Post (18 May 2020); https://www.washingtonpost.com/health/as-coronavirus-testing-expands-a-new-problem-arises-not-enough-people-to-test/2020/05/17/3f3297de-8bcd-11ea-8ac1-bfb250876b7a_story.html
Keeling, M. J. et al. Predictions of COVID-19 dynamics in the UK: short-term forecasting and analysis of potential exit strategies. Preprint at medRxiv https://doi.org/10.1101/2020.05.10.20083683 (2020).
Presidential Proclamation—Travel From Europe (U.S. Department of State, 8 May 2020); https://travel.state.gov/content/travel/en/traveladvisories/presidential-proclamation-travel-from-europe.html
The COVID Tracking Project (The Atlantic, accessed 18 May 2020); https://covidtracking.com/
Data for Good (Unacast, accessed 18 May 2020); https://www.unacast.com/data-for-good
COVID-19 Community Mobility Reports (Google LLC, accessed 15 June 2020); https://www.google.com/covid19/mobility/
The State of the Restaurant Industry (Open Table, accessed 18 May 2020); https://www.opentable.com/state-of-industry
Bois, F. Y. GNU MCSim: Bayesian statistical inference for SBML-coded systems biology models. Bioinformatics 25, 1453–1454 (2009).
Gelman, A. & Rubin, D. B. Inference from iterative simulation using multiple sequences. Stat. Sci. 7, 457–472 (1992).
RStudio (RStudio Team, 2020); https://rstudio.com/
R: The R Project for Statistical Computing (R Core Team, 2020); https://www.r-project.org/
Population and Housing Unit Estimates Dataset, 2010–2019 (United States Census Bureau, accessed 19 May 2020); https://www2.census.gov/programs-surveys/popest/datasets/2010-2019/state/detail/
Lauer, S. A. et al. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann. Intern. Med. https://doi.org/10.7326/M20-0504 (2020).
He, X. et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 26, 672–675 (2020).
Mossong, J. et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 5, e74 (2008).
Verity, R. et al. Estimates of the severity of coronavirus disease 2019: a model-based analysis. Lancet Infect. Dis. 20, 669–677 (2020).
Li, Q. et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N. Engl. J. Med. 382, 1199–1207 (2020).
Riou, J. & Althaus, C. L. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Eurosurveillance 25, 2000058 (2020).
Park, S. W. et al. Reconciling early-outbreak estimates of the basic reproductive number and its uncertainty: a new framework and applications to the novel coronavirus (2019-nCoV) outbreak. J. R. Soc. Interface 17, 20200144 (2020).
America’s COVID Warning System (Covid Act Now, accessed 15 June 2020); https://covidactnow.org/?s=49762
Gao, Z. et al. A systematic review of asymptomatic infections with COVID-19. J. Microbiol. Immunol. Infect. https://doi.org/10.1016/j.jmii.2020.05.001 (2020).
Arons, M. M. et al. Presymptomatic SARS-CoV-2 infections and transmission in a skilled nursing facility. N. Engl. J. Med. 382, 2081–2090 (2020).
Nishiura, H. et al. Estimation of the asymptomatic ratio of novel coronavirus infections (COVID-19). Int. J. Infect. Dis. 94, 154–155 (2020).
Watson, J., Whiting, P. F. & Brush, J. E. Interpreting a covid-19 test result. Brit. Med. J. 369, m1808 (2020).
Cummings, M. J. et al. Epidemiology, clinical course, and outcomes of critically ill adults with COVID-19 in New York City: a prospective cohort study. Lancet 395, 1763–1770 (2020).
Sun, K., Chen, J. & Viboud, C. Early epidemiological analysis of the coronavirus disease 2019 outbreak based on crowdsourced data: a population-level observational study. Lancet Digit. Health 2, e201–e208 (2020).
Onder, G., Rezza, G. & Brusaferro, S. Case-fatality rate and characteristics of patients dying in relation to COVID-19 in Italy. JAMA 323, 1775–1776 (2020).
Map: How States are Reopening after Coronavirus Shutdown (Washington Post, accessed 15 June 2020); https://www.washingtonpost.com/graphics/2020/national/states-reopening-coronavirus-map/
Acknowledgements
We acknowledge funding from the National Science Foundation (no. RAPID DEB 2028632) and National Institutes of Health, National Institute of Environmental Health Sciences (no. P30 ES029067). The funders had no role in the conceptualization, design, data collection, analysis, decision to publish or preparation of the manuscript. We thank F. Y. Bois, J. K. Cetina, M. Giannoni, I. Rusyn and W. Więcek for useful input and advice on scenario development, model formulation and MCMC simulation. We also thank Unacast for making their mobility data available to researchers, and The COVID Tracking Project for compiling case and mortality data and providing these to the public. Portions of this research were conducted with the advanced computing resources provided by Texas A&M High Performance Research Computing.
Author information
Authors and Affiliations
Contributions
W.A.C. and M.L.N.-M. conceived and designed the study and developed the model. W.A.C. performed the analysis. W.A.C. and M.L.N.-M. drafted the paper, with critical revision by R.F.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Charlotte Payne.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Correlations across states between Reff(t) and (A) θmin, (B) η, (C) Δ, and (D) fC.
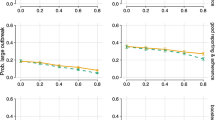
For each state, 500 posterior samples are shown. Substantial state-to-state heterogeneity is evident in all parameters, with η,θmin, rmax, and fC contribute over 50% of the variance in Reff(t) under a linear model (estimated from ANOVA table [Supplementary Table 1] using the sum-of-squares relative to the total sum-of-squares). For θmin, while lower values appear to be associated with greater current values of Reff(t) in a univariate model (linear model coefficient = -0.54, t statistic = -78.14, p < 2.2e-16, 95% CI = [-0.56,-0.53]), the correlation is positive in the multivariate model (coefficient = 0.11, t statistic = 13.65, p < 2.2e-16, 95% CI = [0.09, 0.13]). The other parameters correlate as expected: higher Reff(t) is correlated with lower contribution from hygiene practices (smaller η) (coefficient = -0.39, t statistic = -59.7, p < 2.2e-16, 95% CI = [-0.40,-0.38]), more reopening (larger rmax) (coefficient = 0.44, t statistic = 119.0, p < 2.2e-16, 95% CI = [0.43, 0.45]), and lower rates of contact tracing (smaller fC) (coefficient = -0.90, t statistic = -114.6, p < 2.2e-16, 95% CI = [-0.92, -0.89]).
Extended Data Fig. 2 Contour maps for each state of the probability that Reff(t) at different levels contact tracing fC and testing λ.
Contours are labelled as by median and 95% Credible interval, and current median estimates of fC and λ are shown by the circle.
Extended Data Fig. 3 Estimated testing and contact tracing rates needed for Reff(t) < 1 as of July 22, 2020.
Boxplots (line = median, box = IQR, whiskers = 95% CrI) are filled based on the estimated Reff(t) on July 22, 2020, as shown in the legend. Top panel is changing testing rate alone, the middle panel is changing contact tracing rate alone, and the bottom panel is changing both to the same value. Also shown are the current median estimates of the testing and contact tracing rates.
Extended Data Fig. 4 Estimated testing and contact tracing rates needed for R(t) < 1 with complete re-opening (that is, removal of all social distancing and hygiene mitigation).
Boxplots (line = median, box = IQR, whiskers = 95% CrI) are filled based on the estimated Reff(t) on July 22, 2020, as shown in the legend. Top panel is changing testing rate alone, the middle panel is changing contact tracing rate alone, and the bottom panel is changing both to the same value. Also shown are the current median estimates of the testing and contact tracing rates.
Supplementary information
Supplementary Information
Supplementary Figs. 1–9 and Supplementary Tables 1–3.
Rights and permissions
About this article
Cite this article
Chiu, W.A., Fischer, R. & Ndeffo-Mbah, M.L. State-level needs for social distancing and contact tracing to contain COVID-19 in the United States. Nat Hum Behav 4, 1080–1090 (2020). https://doi.org/10.1038/s41562-020-00969-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41562-020-00969-7
This article is cited by
-
Revealing associations between spatial time series trends of COVID-19 incidence and human mobility: an analysis of bidirectionality and spatiotemporal heterogeneity
International Journal of Health Geographics (2023)
-
Relative role of border restrictions, case finding and contact tracing in controlling SARS-CoV-2 in the presence of undetected transmission: a mathematical modelling study
BMC Medicine (2023)
-
Quantifying the spatial spillover effects of non-pharmaceutical interventions on pandemic risk
International Journal of Health Geographics (2023)
-
Effects of public-health measures for zeroing out different SARS-CoV-2 variants
Nature Communications (2023)
-
Analyzing the effect of restrictions on the COVID-19 outbreak for some US states
Theoretical Ecology (2023)