Abstract
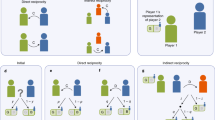
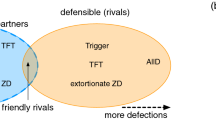
Reciprocity is a major factor in human social life and accounts for a large part of cooperation in our communities. Direct reciprocity arises when repeated interactions occur between the same individuals. The framework of iterated games formalizes this phenomenon. Despite being introduced more than five decades ago, the concept keeps offering beautiful surprises. Recent theoretical research driven by new mathematical tools has proposed a remarkable dichotomy among the crucial strategies: successful individuals either act as partners or as rivals. Rivals strive for unilateral advantages by applying selfish or extortionate strategies. Partners aim to share the payoff for mutual cooperation, but are ready to fight back when being exploited. Which of these behaviours evolves depends on the environment. Whereas small population sizes and a limited number of rounds favour rivalry, partner strategies are selected when populations are large and relationships stable. Only partners allow for evolution of cooperation, while the rivals’ attempt to put themselves first leads to defection.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Change history
27 March 2018
In the version of this Review Article originally published, in Fig. 4 an arrow pointing from ALLC to ALLD was mistakenly omitted. This has now been corrected in all versions of the Review Article.
References
von Neumann, J. & Morgenstern, O. Theory of Games and Economic Behavior (Princeton Univ. Press, Princeton, NJ, 1944).
Nash, J. F. Equilibrium points in n-person games. Proc. Natl Acad. Sci. USA 36, 48–49 (1950).
Flood, M. M. Some experimental games. Manage. Sci. 5, 5–26 (1958).
Rapoport, A. & Chammah, A. M. Prisoner’s Dilemma (Univ. Michigan Press, Ann Arbor, MI, 1965).
Trivers, R. L. The evolution of reciprocal altruism. Q. Rev. Biol. 46, 35–57 (1971).
Nowak, M. A. Evolutionary Dynamics (Harvard Univ. Press, Cambridge, MA, 2006).
Sigmund, K. The Calculus of Selfishness (Princeton Univ. Press, Princeton, NJ, 2010).
Nowak, M. A. Five rules for the evolution of cooperation. Science 314, 1560–1563 (2006).
Smale, S. The prisoner’s dilemma and dynamical systems associated to non-cooperative games. Econometrica 48, 1617–1634 (1980).
Mailath, G. J. & Samuelson, L. Repeated Games and Reputations (Oxford Univ. Press, Oxford, 2006). Extensive compendium on repeated games from an economics point of view, which gives an excellent overview on the folk theorem literature.
Abreu, D. Extremal equilibria of oligopolistic supergames. J. Econ. Theory 39, 191–225 (1986).
Bernheim, D. & Whinston, M. D. Multimarket contact and collusive behavior. Rand J. Econ. 21, 1–26 (1990).
Cable, D. M. & Shane, S. A prisoner’s dilemma approach to entrepreneur–venture capitalist relationships. Acad. Manage. Rev. 22, 142–176 (1997).
Majeski, S. J. Arms races as iterated prisoner’s dilemma games. Math. Soc. Sci. 7, 253–266 (1984).
Aumann, R. J. War and peace. Proc. Natl Acad. Sci. USA 103, 17075–17078 (2006).
Wilkinson, G. S. Reciprocal food-sharing in the vampire bat. Nature 308, 181–184 (1984).
Stephens, D. W., McLinn, C. M. & Stevens, J. R. Discounting and reciprocity in an iterated prisoner’s dilemma. Science 298, 2216–2218 (2002).
Milinski, M. Tit for tat in sticklebacks and the evolution of cooperation. Nature 325, 433–435 (1987).
Ben-Porath, E. The complexity of computing a best response automaton in repeated games with mixed strategies. Games Econ. Behav. 2, 1–12 (1990).
Papadimitriou, C. H. On players with a bounded number of states. Games Econ. Behav. 4, 122–131 (1992).
Friedman, J. A non-cooperative equilibrium for supergames. Rev. Econ. Stud. 38, 1–12 (1971).
Aumann, R. J. in Essays in Game Theory and Mathematical Economics in Honor of Oskar Morgenstern (eds Henn, R. & Moeschlin, O.) 11–42 (Wissenschaftsverlag, Mannheim, 1981).
Maynard Smith, J. Evolution and the Theory of Games (Cambridge Univ. Press, Cambridge, 1982).
Selten, R. & Hammerstein, P. Gaps in Harley’s argument on evolutionarily stable learning rules and in the logic of “Tit for Tat”. Behav. Brain Sci. 7, 115–116 (1984).
Boyd, R. & Lorberbaum, J. No pure strategy is evolutionary stable in the iterated prisoner’s dilemma game. Nature 327, 58–59 (1987).
Bendor, J. & Swistak, P. Types of evolutionary stability and the problem of cooperation. Proc. Natl Acad. Sci. USA 92, 3596–3600 (1995).
van Veelen, M., Garcia, J., Rand, D. G. & Nowak, M. A. Direct reciprocity in structured populations. Proc. Natl Acad. Sci. USA 109, 9929–9934 (2012).
Garcia, J. & van Veelen, M. In and out of equilibrium I: Evolution of strategies in repeated games with discounting. J. Econ. Theory 161, 161–189 (2016).
Boyd, R. Mistakes allow evolutionary stability in the repeated prisoner’s dilemma game. J. Theor. Biol. 136, 47–56 (1989).
Fudenberg, D. & Maskin, E. Evolution and cooperation in noisy repeated games. Am. Econ. Rev. 80, 274–279 (1990).
Nowak, M. A. & Sigmund, K. Chaos and the evolution of cooperation. Proc. Natl Acad. Sci. USA 90, 5091–5094 (1993).
Imhof, L. A., Fudenberg, D. & Nowak, M. A. Evolutionary cycles of cooperation and defection. Proc. Natl Acad. Sci. USA 102, 10797–10800 (2005).
Imhof, L. A. & Nowak, M. A. Stochastic evolutionary dynamics of direct reciprocity. Proc. R. Soc. London Ser. B 277, 463–468 (2010).
Nowak, M. A., Sasaki, A., Taylor, C. & Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650 (2004). Introduces finite population size to evolutionary game dynamics.
Imhof, L. A., Fudenberg, D. & Nowak, M. A. Tit-for-tat or win-stay, lose-shift? J. Theor. Biol. 247, 574–580 (2007).
Garcia, J. & Traulsen, A. The structure of mutations and the evolution of cooperation. PLoS ONE 7, e35287 (2012).
Kurokawa, S. & Ihara, Y. Emergence of cooperation in public goods games. Proc. R. Soc. London Ser. B 276, 1379–1384 (2009).
Martinez-Vaquero, L. A., Cuesta, J. A. & Sanchez, A. Generosity pays in the presence of direct reciprocity: a comprehensive study of 2×2 repeated games. PLoS ONE 7, e35135 (2012).
Baek, S. K., Jeong, H. C., Hilbe, C. & Nowak, M. A. Comparing reactive and memory-one strategies of direct reciprocity. Sci. Rep. 6, 25676 (2016).
Axelrod, R. The Evolution of Cooperation (Basic Books, New York, NY, 1984). Axelrod’s tournament and the success of tit-for-tat have been transformative for the field; this book contains a detailed analysis of the tournament’s results .
Molander, P. The optimal level of generosity in a selfish, uncertain environment. J. Conflict Resolut. 29, 611–618 (1985).
Nowak, M. A. & Sigmund, K. Tit for tat in heterogeneous populations. Nature 355, 250–253 (1992).
Nowak, M. A. & Sigmund, K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the prisoner’s dilemma game. Nature 364, 56–58 (1993). Describes a simple yet surprisingly powerful strategy to maintain cooperation in noisy repeated games, win-stay, lose-shift.
Kraines, D. P. & Kraines, V. Y. Pavlov and the prisoner’s dilemma. Theory Decis. 26, 47–79 (1989).
Lindgren, K. in The Economy as an Evolving Complex System II (eds Arthur, W. B., Durlauf, S. N. & Lane, D. A.) 337–368 (Addison-Wesley, Reading, MA, 1997).
Hauert, C. & Schuster, H. G. Effects of increasing the number of players and memory size in the iterated prisoner’s dilemma: a numerical approach. Proc. R. Soc. London Ser. B 264, 513–519 (1997).
Pinheiro, F. L., Vasconcelos, V. V., Santos, F. C. & Pacheco, J. M. Evolution of all-or-none strategies in repeated public goods dilemmas. PLoS Comput. Biol. 10, e1003945 (2014).
Hilbe, C., Martinez-Vaquero, L. A., Chatterjee, K. & Nowak, M. A. Memory-n strategies of direct reciprocity. Proc. Natl Acad. Sci. USA 114, 4715–4720 (2017).
Fischer, I. et al. Fusing enacted and expected mimicry generates a winning strategy that promotes the evolution of cooperation. Proc. Natl Acad. Sci. USA 110, 10229–10233 (2013).
Yi, S. D., Baek, S. K. & Choi, J.-K. Combination with anti-tit-for-tat remedies problems of tit-for-tat. J. Theor. Biol. 412, 1–7 (2017).
Duersch, P., Oechssler, J. & Schipper, B. When is tit-for-tat unbeatable? Int. J. Game Theory 43, 25–36 (2013).
Rapoport, A., Seale, D. A. & Colman, A. M. Is tit-for-tat the answer? On the conclusions drawn from axelrod’s tournaments. PLoS ONE 10, e0134128 (2015).
Bendor, J. In good times and bad: reciprocity in an uncertain world. Am. J. Polit. Sci. 31, 531–558 (1987).
Nowak, M. A., Sigmund, K. & El-Sedy, E. Automata, repeated games and noise. J. Math. Biol. 33, 703–722 (1995).
Brandt, H. & Sigmund, K. The good, the bad and the discriminator — errors in direct and indirect reciprocity. J. Theor. Biol. 239, 183–194 (2006).
Hofbauer, J. & Sigmund, K. Evolutionary Games and Population Dynamics (Cambridge Univ. Press, Cambridge, 1998).
Cressman, R. Evolutionary Dynamics and Extensive Form Games (MIT Press, Cambridge, MA, 2003).
Nowak, M. A. & Sigmund, K. The evolution of stochastic strategies in the prisoner’s dilemma. Acta Appl. Math. 20, 247–265 (1990).
Press, W. H. & Dyson, F. Iterated prisoner’s dilemma contains strategies that dominate any evolutionary opponent. Proc. Natl Acad. Sci. USA 109, 10409–10413 (2012). Using innovative mathematical concepts, Press and Dyson show there are strategies for the repeated prisoner’s dilemma that allow players to extort their opponents.
Chen, J. & Zinger, A. The robustness of zero-determinant strategies in iterated prisoner’s dilemma games. J. Theor. Biol. 357, 46–54 (2014).
Pan, L., Hao, D., Rong, Z. & Zhou, T. Zero-determinant strategies in iterated public goods game. Sci. Rep. 5, 13096 (2015).
McAvoy, A. & Hauert, C. Autocratic strategies for iterated games with arbitrary action spaces. Proc. Natl Acad. Sci. USA 113, 3573–3578 (2016).
McAvoy, A. & Hauert, C. Autocratic strategies for alternating games. Theor. Popul. Biol. 113, 13–22 (2016).
Ichinose, G. & Masuda, N. Zero-determinant strategies in finitely repeated games. J. Theor. Biol. 438, 61–77 (2018).
Hilbe, C., Nowak, M. A. & Sigmund, K. The evolution of extortion in iterated prisoner’s dilemma games. Proc. Natl Acad. Sci. USA 110, 6913–6918 (2013). Based on computer simulations, this article suggests that extortionate strategies can only succeed in small populations, or when two populations evolve at different rates.
Hilbe, C., Nowak, M. A. & Traulsen, A. Adaptive dynamics of exortion and compliance. PLoS ONE 8, e77886 (2013).
Szolnoki, A. & Perc, M. Evolution of extortion in structured populations. Phys. Rev. E 89, 022804 (2014).
Szolnoki, A. & Perc, M. Defection and extortion as unexpected catalysts of unconditional cooperation in structured populations. Sci. Rep. 4, 5496 (2014).
Adami, C. & Hintze, A. Evolutionary instability of zero-determinant strategies demonstrates that winning is not everything. Nat. Commun. 4, 2193 (2013).
Wu, Z.-X. & Rong, Z. Boosting cooperation by involving extortion in spatial prisoner’s dilemma games. Phys. Rev. E 90, 062102 (2014).
Hilbe, C., Röhl, T. & Milinski, M. Extortion subdues human players but is finally punished in the prisoner’s dilemma. Nat. Commun. 5, 3976 (2014).
Xu, B., Zhou, Y., Lien, J. W., Zheng, J. & Wang, Z. Extortion can outperform generosity in iterated prisoner’s dilemma. Nat. Commun. 7, 11125 (2016).
Milinski, M., Hilbe, C., Semmann, D., Sommerfeld, R. D. & Marotzke, J. Humans choose representatives who enforce cooperation in social dilemmas through extortion. Nat. Commun. 7, 10915 (2016).
Hilbe, C., Hagel, K. & Milinski, M. Asymmetric power boosts extortion in an economic experiment. PLoS ONE 11, e0163867 (2016).
Hilbe, C., Wu, B., Traulsen, A. & Nowak, M. A. Cooperation and control in multiplayer social dilemmas. Proc. Natl Acad. Sci. USA 111, 16425–16430 (2014).
Stewart, A. J. & Plotkin, J. B. From extortion to generosity, evolution in the iterated prisoner’s dilemma. Proc. Natl Acad. Sci. USA 110, 15348–15353 (2013). This study shows that large evolving populations favour the emergence of generous strategies, and introduces the important concept of evolutionary robustness.
Stewart, A. J. & Plotkin, J. B. Collapse of cooperation in evolving games. Proc. Natl Acad. Sci. USA 111, 17558–17563 (2014). Describes all evolutionary robust strategies for iterated 2 × 2 games.
Stewart, A. J. & Plotkin, J. B. Small groups and long memories promote cooperation. Sci. Rep. 6, 26889 (2016).
Stewart, A. J., Parsons, T. L. & Plotkin, J. B. Evolutionary consequences of behavioral diversity. Proc. Natl Acad. Sci. USA 113, E7003–E7009 (2016).
Akin, E. in Ergodic Theory, Advances in Dynamics (ed. Assani, I.) 77–107 (de Gruyter, Berlin, 2016). Based on the mathematical formalism of zero-determinant strategies, Akin characterized all memory-1 partner strategies (called ‘good strategies’ in this article).
Akin, E. What you gotta know to play good in the iterated prisoner’s dilemma. Games 6, 175–190 (2015).
Akin, E. Good strategies for the iterated prisoner’s dilemma: Smale vs. Markov. J. Dynam. Games 4, 217–253 (2017).
Hilbe, C., Traulsen, A. & Sigmund, K. Partners or rivals? Strategies for the iterated prisoner’s dilemma. Games Econ. Behav. 92, 41–52 (2015). Introduces the notion of competitive rival strategies, and describes partner and rival strategies for the repeated prisoner’s dilemma with discounted payoffs.
van den Berg, P., Molleman, L. & Weissing, F. J. Focus on the success of others leads to selfish behavior. Proc. Natl Acad. Sci. USA 112, 2912–2917 (2015).
Dal Bó, P. Cooperation under the shadow of the future: experimental evidence from infinitely repeated games. Am. Econ. Rev. 95, 1594–1604 (2005).
Blonski, M., Ockenfels, P. & Spagnolo, G. Equilibrium selection in the repeated prisoner’s dilemma: axiomatic approach and experimental evidence. Am. Econ. J. Microecon 3, 164–192 (2011).
Fudenberg, D., Dreber, A. & Rand, D. G. Slow to anger and fast to forgive: cooperation in an uncertain world. Am. Econ. Rev. 102, 720–749 (2012).
Doebeli, M. & Hauert, C. Models of cooperation based on the prisoner’s dilemma and the snowdrift game. Ecol. Lett. 8, 748–766 (2005).
Nowak, M. A. Evolving cooperation. J. Theor. Biol. 299, 1–8 (2012).
Frean, M. R. The prisoner’s dilemma without synchrony. Proc. R. Soc. London Ser. B 257, 75–79 (1994).
Nowak, M. A. & Sigmund, K. The alternating prisoner’s dilemma. J. Theor. Biol. 168, 219–226 (1994).
Zagorsky, B. M., Reiter, J. G., Chatterjee, K. & Nowak, M. A. Forgiver triumphs in alternating prisoner’s dilemma. PLoS ONE 8, e80814 (2013).
Roberts, G. & Sherratt, T. N. Development of cooperative relationships through increasing investment. Nature 394, 175–179 (1998).
Wahl, L. M. & Nowak, M. A. The continuous prisoner’s dilemma: I. Linear reactive strategies. J. Theor. Biol. 200, 307–321 (1999).
Killingback, T. & Doebeli, M. The continuous prisoner’s dilemma and the evolution of cooperation through reciprocal altruism with variable investment. Am. Nat. 160, 421–438 (2002).
Gokhale, C. S. & Traulsen, A. Evolutionary games in the multiverse. Proc. Natl Acad. Sci. USA 107, 5500–5504 (2010).
Traulsen, A., Nowak, M. A. & Pacheco, J. M. Stochastic dynamics of invasion and fixation. Phys. Rev. E 74, 011909 (2006).
Fudenberg, D. & Imhof, L. A. Imitation processes with small mutations. J. Econ. Theory 131, 251–262 (2006).
Wu, B., Gokhale, C. S., Wang, L. & Traulsen, A. How small are small mutation rates? J. Math. Biol. 64, 803–827 (2012).
Boerlijst, M. C., Nowak, M. A. & Sigmund, K. Equal pay for all prisoners. Am. Math. Mon. 104, 303–307 (1997).
Acknowledgements
This work was supported by the European Research Council Start Grant 279307: Graph Games (to K.C.), Austrian Science Fund (FWF) Grant P23499-N23 (to K.C.), FWF NFN Grant S11407-N23 Rigorous Systems Engineering/Systematic Methods in Systems Engineering (to K.C.), Office of Naval Research Grant N00014-16-1- 2914 (to M.A.N.) and the John Templeton Foundation (M.A.N.). C.H. acknowledges generous support from the ISTFELLOW programme.
Author information
Authors and Affiliations
Contributions
All authors conceived the study, performed the analysis and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures 1 and 2
Rights and permissions
About this article
Cite this article
Hilbe, C., Chatterjee, K. & Nowak, M.A. Partners and rivals in direct reciprocity. Nat Hum Behav 2, 469–477 (2018). https://doi.org/10.1038/s41562-018-0320-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41562-018-0320-9
This article is cited by
-
Effect of reciprocity mechanisms on evolutionary dynamics in feedback-evolving games
Nonlinear Dynamics (2024)
-
The effect of environmental information on evolution of cooperation in stochastic games
Nature Communications (2023)
-
Quantitative assessment can stabilize indirect reciprocity under imperfect information
Nature Communications (2023)
-
Personal sustained cooperation based on networked evolutionary game theory
Scientific Reports (2023)
-
Evolutionary Games and Applications: Fifty Years of ‘The Logic of Animal Conflict’
Dynamic Games and Applications (2023)