Abstract
Recent studies increasingly recognize the importance of critical-zone weathering during mountain building for long-term CO2 drawdown and release. However, the focus on near-surface weathering reactions commonly does not account for CO2 emissions from the crust, which could outstrip CO2 drawdown where carbonates melt and decarbonize during subduction and metamorphism. We analyse water chemistry from streams in Italy’s central Apennines that cross a gradient in heat flow and crustal thickness with relatively constant climatic conditions. We quantify the balance of inorganic carbon fluxes from near-surface weathering processes, metamorphism and the melting of carbonates. We find that, at the regional scale, carbon emissions from crustal sources outpace near-surface fluxes by two orders of magnitude above a tear in the subducting slab characterized by heat flow greater than 150 mW m–2 and crustal thickness of less than 25 km. By contrast, weathering processes dominate the carbon budget where crustal thickness exceeds 40 km and heat flow is lower than 30 mW m–2. The observed variation in metamorphic fluxes is one to two orders of magnitude larger than that of weathering fluxes. We therefore suggest that geodynamic modulations of metamorphic melting and decarbonation reactions are an efficient process by which tectonics can regulate the inorganic carbon cycle.
Similar content being viewed by others
Main
Global plate motions impact Earth’s carbon cycle by modulating both the release of CO2 from the crust and mantle1 and the emission or sequestration of CO2 from rock weathering2. In uplifting mountains, near-surface (critical-zone) chemical weathering reactions are particularly efficient3, resulting in timescale-dependent changes in the CO2 content of the atmosphere through silicate and carbonate mineral weathering with carbonic acid (H2CO3) and sulfuric acid (H2SO4). Thus, orogenesis is proposed to impact global climate by increasing the weatherability of Earth’s surface4,5. However, mountain building can also generate large volumes of ‘metamorphic’ CO2 from the decarbonation or melting of carbonate in the crust and mantle1,6,7,8, where orogenesis involves the collision and subduction of carbonate rock. This release of CO2 ultimately reflects the conversion of carbonate to weatherable silicate minerals that completes the global silicate weathering cycle9. However, the different timescales required for metamorphic CO2 release and silicate weathering suggest mountain building may impact global climate through the modulation of these deep CO2 emissions10,11.
Determining the role of orogenesis in the global carbon cycle requires direct comparisons of its impact on both deep processes and chemical weathering. To our knowledge, such comparisons exist for only two locations. In the New Zealand Southern Alps, collision of mostly siliceous rocks results in degassing-related CO2 emission fluxes, which are an order of magnitude smaller than inferred CO2 drawdown fluxes from silicate weathering12. In the Himalaya, the subduction and collision of carbonates lead to CO2 degassing that outpaces silicate weathering fluxes13,14. These studies estimate metamorphic CO2 degassing directly from samples in springs, aquifers and gas vents, whereas weathering fluxes are estimated from riverine fluxes. Therefore, these datasets cannot constrain how deep, crustal or mantle-derived CO2 fluxes interact with the critical zone and may be buffered by carbonate and silicate weathering. Moreover, it remains unclear how geodynamics—the influence of mantle convection on tectonics—impact the relative spatial importance of degassing and weathering fluxes across a mountain range.
To address this important knowledge gap in the inorganic carbon cycle, we investigate the relationship between deep CO2 release and chemical weathering in the critical zone along a geodynamic gradient in the central Apennines (Italy), an active mountain range that exposes and subducts large volumes of carbonate. We present major riverine element and isotope data from two large catchments that straddle a gradient in crustal thickness and heat flow above a tear and area of retreat within the subducting slab and assess inorganic CO2 emission and sequestration fluxes associated with critical zone and deep processes. We use an inverse approach to apportion the solute flux to the weathering of carbonates, silicates and sulfide and to distinguish atmospheric, lithologic and metamorphic CO2 sources. The results of this study demonstrate that the inorganic carbon budget of the central Apennines is controlled primarily by metamorphic release that varies strongly across the regional geodynamic gradient. Hence, the impact of regional tectonics on CO2 sources may be substantially larger than tectonic modulation of CO2 sinks.
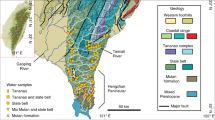
Tectonic setting of the central Apennines
The Apennine chain is a fold-and-thrust belt characterized by an accretionary wedge to the east and a back-arc extensional basin to the west15 (Fig. 1 and Supplementary Text 1), which developed through syn-convergent extension, due to the subduction and rollback of the Adriatic slab beneath Eurasia16. This dynamic has produced a tectonic gradient expressed by an increase in extension from east to west, resulting in lower crustal thickness (~20 km) and higher heat flow (>200 mW m–2) in the west relative to thicker crust (>40 km) and lower heat flow (<30 mW m–2) in the east8,17,18 (Fig. 1d). In the central Apennines, the absence of intermediate seismicity and the presence of anomalously low P-wave velocities have been interpreted as a slab window8,19,20 formed due to progressive east-directed rollback and tearing of the Adriatic slab. By contrast, intermediate and deep seismicity beneath the northern Apennines and Calabria illustrate an intact, subducting slab20.
a, Location of studied catchments (pink outlines) and location of the cross-section shown in e. b, Sample distribution (black circles) and river networks. Networks for the studied rivers are shown in blue, and adjacent river networks are shown in black. c, Simplified geologic map. d, Geodynamic setting for the central Apennines. Moho depth is illustrated as a colour gradient. Heat-flow isotherms are illustrated as contour lines for a 10 mW m–2 contour interval (dashed lines) or a 50 mW m–2 contour interval (solid line) unless otherwise noted. e, Geologic cross-section through the Italian peninsula. The cross-section illustrates the ages, lithologies and major tectonic structures in the upper 20 km of the crust. Layers in b–d are overlain on a Shuttle Radar Topography Mission (SRTM) 90 m hillshade and digital elevation model. All individual sample points are shown in Extended Data Fig. 1. Panels adapted with permission from: c, refs. 22,23 under a Creative Commons license CC BY 3.0; d, ref. 46, Oxford University Press; ref. 17, Springer; ref. 8, Elsevier; e, ref. 15, The Virtual Explorer Pty Ltd.
Water chemistry of the Tevere and Aterno-Pescara rivers
We present 104 water samples collected during winter 2021 (55) and summer 2020 (49) from these catchments (Fig. 1 and Extended Data Fig. 1), which were selected to maximize areal coverage and to sample different lithologies and water bodies (for example, river, springs/groundwater, lakes), to understand the potential sources of dissolved ions to the river channels. For all samples, we measured concentrations of dissolved major elements as well as isotopes of inorganic carbon (δ13C, F14C (fraction modern carbon)) and sulfur and oxygen in sulfate (δ34S, δ18O(SO4)). On the basis of these measurements, we can unmix the contributions to the dissolved load of carbonate, silicate and evaporite mineral sources (Methods). In addition, we distinguish the acid sources for weathering, including sulfuric acid (H2SO4), carbonic acid (H2CO3) derived from biogenic or atmospheric CO2 and H2CO3 derived from metamorphic carbon.
Because the weathering of carbonate versus silicate rocks can have different implications for the inorganic carbon cycle, we broadly categorize the lithology at each sampling location as ‘carbonate’, ‘siliciclastic’ or ‘mixed’ (a carbonate-siliciclastic mix)21 on the basis of the distribution of surface lithologies in refs. 22,23. The weathering of silicate or carbonate rock by H2CO3 or H2SO4 co-determines the resulting production of ions and dissolved inorganic carbon (DIC)24. In the absence of a gypsum contribution, the ratios of [SO42−]/[Σ+] and [Ca2+]/[Σ+] (where Σ+ is the sum of cations) reflect the balance of carbonate and silicate weathering with a mixture of H2CO3 and H2SO4 sources. Most river samples have ratios of [SO42−]/[Σ+] below 0.45 and [Ca2+]/[Σ+] ratios between ~0.3 and 0.9 (Fig. 2a,b). The siliciclastic samples and a subset of numbered Tevere samples collected at or near springs display the lowest [Ca2+]/[Σ+] ratios. Cations in these samples are dominated by Na+, rather than Ca2+, and the similarity between [Na+] and [Cl−] in these samples suggests that halite is probably the primary source of [Na+] (ref. 21). Overall, the high [Ca2+]/[Σ+] and low [SO42−]/[Σ+] values of the samples suggest that the study area is dominated by H2CO3 weathering of carbonate and silicate rock.
a,b, Ratios of [Ca2+]/[Σ+] plotted against ratios of [SO42−]/[Σ+] for winter samples (a) and summer samples (b). c,d, δ13C plotted against F14C for winter samples (c) and summer samples (d). Samples are coloured by the dominant lithology in the upstream area21: carbonate, mixed carbonate and siliciclastic, or siliciclastic. Bars represent ion or isotopic endmember compositions21. Annotated samples in a and b are samples with low [Ca2+]/[Σ+] that have higher [Na+] than [Ca2+] and reflect evaporite δ34S and δ18O(SO4) signatures.
Carbon isotopes and major element geochemistry yield insights into the proportions of DIC sourced from modern carbon (F14C = 1; for example, biogenic or atmospheric carbon) and from rock-derived, radiocarbon dead sources (F14C = 0; for example, from carbonate weathering or metamorphic carbon). Both δ13C and F14C values are highly variable and reflect these different carbon sources (Fig. 2c,d). Most samples lie between the biogenic (modern) carbon and the carbonate–H2CO3 endmembers, while approximately 30% of samples lie beyond the carbonate–H2CO3 endmember. These low F14C and enriched δ13C values could be explained by H2SO4 dissolution of carbonates25; however, major element chemistry is inconsistent with such large contributions of H2SO4 to the weathering budget (Extended Data Fig. 2). Hence, the low F14C and enriched δ13C values require that a substantial proportion of the H2CO3 is derived from upwelling of deeper, rock-derived CO2-rich fluids8.
Studies in the central Apennines from the past two decades have identified δ13C-enriched sources of CO2 at cold and thermal mineralized springs26,27,28 and in the regional aquifers29, as well as CO2 degassing from localized gas vents. The geochemical (4He/3He) signature of CO2 emissions suggests that degassing fluxes are sourced predominantly from melting of the carbonate sedimentary cover on the subducting Adriatic slab within the mantle lithosphere8,30,31, producing carbonate-rich melts that upwell through the mantle8. Additional CO2 derives from decarbonation of carbonates in the overriding Eurasian plate30. Localized metamorphic CO2 outgassing has been linked with periods of high seismicity16,32,33, suggesting that widespread normal faults and fractures are effective conduits for CO2-rich fluids that migrate through the crust34 (Fig. 1c,e). On reaching the surface, the CO2 either is outgassed at vents28 or mixes with meteoric water in the regional carbonate aquifers and can be released at springs8,35,36. Our chemical analysis of the stream waters suggests that CO2 not only is directly degassed but effectively interacts with the critical zone by providing H2CO3 that can weather carbonate and silicate rocks near the surface.
A CO2 budget for the central Apennines
To quantitatively deconvolve the sources of DIC and contributions of lithologic endmembers to central Apennine rivers, we use a recent inverse model, Mixing Elements and Dissolved Isotopes in Rivers (MEANDIR)37. We quantify the fraction of major ions (Ca2+, Na+, Mg2+, SO42+, Cl−) contributed from silicates, carbonates, evaporites, pyrite oxidation and meteoric water, as well as the fraction of DIC from biogenic carbon, rock-derived carbon, and atmospheric carbon and meteoric water (Methods). The pyrite oxidation endmember allows us to quantify the proportion of weathering by H2SO4. Together with the relative proportions of biogenic and rock-derived carbon, it further allows us to constrain the fraction of carbon derived from deep sources. Where possible, we convert ion concentrations to fluxes by multiplying molar masses of the respective ion with ion concentrations and available run-off estimates averaged over the months of data collection (Methods). We note that our model inputs of Ca2+, HCO3− and δ13C are corrected for the effects of secondary carbonate precipitation, which accounts for the loss of 45% of [Ca2+] for locations included in our carbon budget21. After this correction, estimates of [DIC] increase by 0–181% ([DIC]Corr) and metamorphic CO2 fluxes are 0–45% higher21.
We follow previous work38 and infer CO2 sequestration and release from our fluxes on timescales longer than the compensation of alkalinity fluxes to the ocean by carbonate precipitation (1–10 kyr) (ref. 39) but shorter than the timescales for sulfur reduction in the ocean (>10 Myr)39. We find that the solute and carbon budget of the main rivers in the study area are variable in space and related to the geomorphic setting. In the Aterno-Pescara River, CO2 fluxes (reported in tons of carbon (tC) per area per time) are dominated by silicate weathering (−0.4–0 tC km–2 yr–1), with minor fluxes from coupled pyrite oxidation and carbonate weathering (0–0.1 tC km–2 yr–1) but no measurable metamorphic carbon fluxes (Fig. 3), with the exception of springs or small tributaries near or along faults (Extended Data Figs. 3–6). CO2 fluxes from pyrite oxidation (0–0.2 tC km2 yr–1) and silicate weathering (−1.1–0 tC km2 yr–1) in the Tevere River are of similar magnitude to the Aterno-Pescara River. However, the net CO2 fluxes in the Tevere are 1–2 orders of magnitude higher than in the Aterno-Pescara River due to large CO2 fluxes inferred from metamorphic carbon (Fig. 3). In the largest Tevere tributaries, the flux of metamorphic CO2 is consistently 1−2 orders of magnitude higher than fluxes from silicate weathering and pyrite oxidation, respectively (Fig. 3)21. While smaller tributaries that drain siliciclastic-rich lithologies are dominated by silicate weathering (Extended Data Figs. 3–6), the regional inorganic carbon budget shows that the central Apennines are a net carbon source.
Regional inorganic CO2 fluxes from five sampling locations with the largest upstream drainage area. a, The sampling locations, site numbers21 and closest discharge stations. Upstream catchment areas from each sampling location are outlined in black and coloured in grey, and the corresponding drainage network (blue lines) is shown. Note that the upstream area for site 45 also includes the area encompassed by site 42. b, Enlarged image of Aterno-Pescara sampling locations and discharge stations. c, CO2 exchange with the atmosphere, shown as fluxes associated with mechanisms that result in long-term CO2 drawdown (silicate weathering) or CO2 release (pyrite oxidation and metamorphic carbon). The sum of the fluxes is illustrated as the total CO2 exchange with the atmosphere. Data bars represent mean values ± 1σ (ref. 21).
Our field seasons broadly reflect the hottest and driest or wettest and coldest times of the year40, allowing us to estimate minimum (summer) and maximum (winter) yearly CO2 fluxes. We calculate a minimum net CO2 flux of 7.9 ± 2.4 tC km–2 yr–1 over an area of 18,243 km2 (Sites 5, 45 and 46) and a maximum estimate of 16.4 ± 6.3 tC km–2 yr–1 over an area of 18,655 km2 (Sites 1, 5, 8, 45 and 46). Overall, the weighted yearly average net CO2 flux is 12.3 ± 4.1 tC km–2 yr–1 (Sites 5, 45 and 46). Relative to a yearly metamorphic CO2 flux upscaled from spring data (28 tC km–2 yr–1) (ref. 29), our estimate of CO2 fluxes is about a factor of 2 lower. These two values probably constitute minimum and maximum estimates, respectively, and their difference could be due to two reasons. First, our river estimates may underestimate CO2 fluxes because they miss rapid, diffusion-controlled CO2 degassing that is not associated with secondary precipitation of carbonate and has a negligible effect on the carbon isotopic composition of the water41. Second, upscaled fluxes from springs to the entire watersheds could overestimate the regional flux of CO2, because they miss diffuse inputs of water across the catchments that can represent between ~20% and 100% of riverine major ion concentrations42. Despite these uncertainties, we can conclude that CO2 fluxes from metamorphic carbon in the Tevere River are orders of magnitude larger than CO2 drawdown fluxes from silicate weathering in these watersheds.
To estimate a total carbon budget for the Apennines, we combine our results with estimates for inorganic CO2 emissions from gas vents and organic CO2 exchanges2. Discrete CO2 emissions from gas vents reported on the western side of the Apennines contribute 2–12 tC km–2 yr–1 over an estimated area of 52,000 km2 (Fig. 4)8,36. Estimates for petrogenic organic carbon oxidation do not exist for the Apennines but are probably small in these lithologies—analogous to the small sulfide oxidation rates. Particulate organic carbon export at 200 m depth in the Tyrrhenian Sea ranges from 1.3 to 6.1 tC km–2 yr–1 for spring and summer and is 0.7 tC km–2 yr–1 in the Adriatic Sea during autumn43. Estimates for dissolved organic carbon burial are lacking, but dissolved organic carbon export is probably much smaller than the particulate organic carbon export44. The central Apennines are thus a net carbon source on the western side of the mountain range, where CO2 emissions from metamorphic decarbonation are 2–10 times larger than organic carbon burial and 1–2 orders of magnitude larger than CO2 drawdown from silicate weathering. On the eastern side, the inorganic CO2 budget is dominated by silicate weathering and CO2-releasing sulfide oxidation from carbonate weathering, although the magnitude of carbon sources is much smaller relative to the western side of the range, so they may be compensated by organic carbon burial.
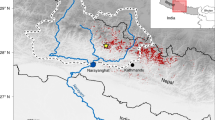
a, Coloured circles and squares illustrate samples with non-zero yearly average HCO3 from metamorphic carbon, scaled by the concentration21. Where both winter and summer concentrations were available for a sample, the symbol represents an average over the two seasons. White-outlined circles and squares illustrate samples where HCO3 from metamorphic CO2 is zero. The purple line marks the boundary between P-wave velocity (Vp) anomalies at 52 km depth; CAW and SAW on the dashed portion of the line highlight the locations of slab windows in the Central and Southern Apennines, respectively. The orange overlay illustrates the spatial extent of measured CO2 gas emissions, grey circles illustrate the locations and depths of seismicity deeper than 40 km and magnitude 3 or higher, and the black sawtoothed line marks the subduction front. b, Enlarged view of the results within the study area, including the locations of normal faults (black lines). Figure adapted with permission from refs. 8,47,48, Elsevier; ref. 49 under a Creative Commons license CC BY 4.0.
Impact of geodynamic setting on the inorganic CO2 budget
The stark difference in both the sources of CO2 and the magnitude of CO2 fluxes between the Tevere (Tyrrhenian side) and Aterno-Pescara Rivers (Adriatic side) coincides with a regional east to west geodynamic and tectonic gradient defined by a westward increase in extension and heat flow and a decrease in crustal thickness8,17,18 (Figs. 1d, 5). In contrast, climatic and lithologic differences between the two river systems are small. We propose that thin crust with high heat flow in the Tevere River drives important release of metamorphic CO2 (Figs. 3–5). In turn, higher crustal thickness and lower heat flow in the Aterno-Pescara River inhibit substantial CO2 release. Here only springs and river samples along or near faults provide evidence for metamorphic CO2 release (Fig. 4), and the composition of catchment-averaged river samples of the Aterno-Pescara River can be explained without any metamorphic inputs. The geodynamic control on CO2 release is also evident from the pattern of metamorphic CO2 emissions measured from local gas vents36 that are primarily on the Tyrrhenian side of the mountain range or are found almost exclusively along faults on the Adriatic side of the range (Fig. 4). This area coincides with the location of the slab window (CAW) (Fig. 4), whereas CO2 emissions have not been reported in Calabria and in the northern Apennines, where a subducting slab is still intact. Slab retreat and break-off have acted as a catalyst for regional mantle convection and increased heat flow19,20,16, which in turn facilitated melting and decarbonation of the carbonate sedimentary cover on the Adriatic plate8. Mantle upwelling induced by the slab dynamics is also responsible for driving long-wavelength uplift19,16, which in turn activated the extensional structures that bring metamorphic CO2 to the surface34. Due to the apparent link between the location of CO2 release with slab retreat and tearing, the timing of slab detachment (~2 Ma)20, and normal fault activation (2.5 and 3.3 Ma), we suggest that the dominance of metamorphic CO2 release on the Tyrrhenian side—and potentially the east–west contrast in the inorganic carbon budget—may have been present over at least 2 Ma.
The east–west patterns of CO2 fluxes, heat flow8,17 and Moho depth46 across the Central Apennines. a, The location of the cross-section from A to A′ is shown in the inset. b, The intersections of the heat flow and Moho depth data with the locations of the Tevere and Aterno-Pescara catchments are illustrated with orange and blue shaded areas, respectively.
The large differences in the riverine solute budget between the two major Apennine river systems, the location of reported CO2 gas emissions and the absence of major climatic or lithologic gradients across the study area support the notion that differences in crustal thickness and heat flow could cause order-of-magnitude variations in inorganic CO2 cycling over length scales of a few tens of kilometres (Fig. 5). Importantly, the variations in the flux of metamorphic CO2 release are much larger than variations in chemical weathering fluxes across the study area. Thus, in the central Apennines, the regional geodynamics and tectonics impact mountain building and the carbon cycle most significantly by modulating the release of metamorphic CO2, not by enhancing CO2 drawdown or release from critical-zone weathering reactions45. Furthermore, the subduction of passive margin carbonate-rich sediments and extension-induced variations in heat flow and crustal thickness reflect orogenic processes common to other mountain ranges during the initial stages of orogenesis1. We suggest that modelling and understanding the true impact of early-stage mountain building on the global carbon cycle should consider the broader role of geodynamics and tectonics beyond uplift and the balance of critical-zone weathering reactions.
Methods
Ion and isotope measurements
For each sample location, we collected water in high-density polyethylene bottles for cations (30 ml), anions (60 ml), alkalinity (250 ml) and δ34S and δ18O(SO42−) (250 ml) analyses. We filtered water samples in the field with 0.2 μm VWR filters and acidified cation samples with two drops of ultra-pure 36% HNO3. We also collected water in glass vials for δ13C and δ14C (20 ml) analyses. We measured the alkalinity of each sample within 24 hours of collection using Gran Titration with a Hach digital titrator. All samples were kept at the German Research Centre for Geosciences (GFZ) in cold storage at 4 °C before analysis.
To deconvolve the major lithologies being weathered in the Central Apennines, we measured the concentrations of major dissolved ions for each water sample. We measured major cations (Ca2+, K+, Mg2+, Na+) and dissolved silica on a Varian 720ES inductively coupled plasma optical emission spectroscope at the GFZ. To monitor machine drift, quality control samples were run for every ten measured samples, and accepted runs had a drift of <5%. We performed quality control tests using water standards SLRS-6 and USGS-T187. A set of 11 in-house standards were used to calibrate the cation measurements, and only those standards that fell within 10% of a linear fit through all standards were accepted. Similarly, we accepted only cation measurements within the range of the accepted standards. Measurement uncertainty was estimated from the maximum deviation of the calibration standards from the calibration line.
We measured major anions (F-, Cl−, SO42−) at the GFZ on a Dionex ICS-1100 chromatograph. Quality control was performed using a six-point linear calibration and USGS-206 and USGS-212 standards. We quantified measurement uncertainty on the basis of the standard deviation of three repeat measurements.
To distinguish between lithologic sources of riverine sulfate, we measured δ34S and δ18O(SO4) at the Centre de Recherche Pétrographiques et Géochimiques. The δ34S samples were prepared according to ref. 50. We extracted anions from water samples using column chemistry, with cationic resin AG1X8, and subsequently dried down and diluted the samples in 5% HNO3. We measured δ34S using a Thermo Fischer Scientific multicollector inductively coupled plasma mass spectrometer Neptune Plus (IRISS platform). Values are provided in the Vienna Canyon Diablo Troilite scale, thanks to an in-house bracketing standard calibrated against the International Atomic Energy Agency (IAEA) S1 standard51. External reproducibility is based on independently purified replicates of seawater, which had average measured δ34S values of 21.2 ± 0.12‰ (summer) and 21.2 ± 0.05‰ (winter), reported with 2σ errors.
We prepared δ18O(SO4) samples by measuring 250 ml of river water and acidifying the solution with HCl 3 N to a pH of 4.2 to eliminate HCO3 and CO3. The initial 250 ml of water was then heated to 200 °C for 30 minutes to eliminate CO2. The temperature was then adjusted to 70 °C, and a 5% BaCl2 solution was added to the water in a volume proportional to the measured concentration of SO4 in the individual water sample. The BaSO4 was allowed to precipitate from the solution for 1 hour, and then overnight at the ambient temperature. The precipitate was filtered using a 0.2 μm Nylon filter and subsequently rinsed twice with distilled water and three times with acidified water (5 ml HCl per litre water). The precipitate was then dried at 100 °C. We measured the δ18O(SO4) on a Thermo Fisher EAlsolink-Delta V isotope ratio mass spectrometer. Measured standards yielded δ18O(SO4) values of 23.3 ± 0.4‰ (IAEA) and 9.3 ± 0.4‰ (NBS 127) for the winter sample set, and 23.3 ± 0.8‰ (IAEA) and 9.3 ± 0.6‰ (NBS 127) for the summer sample set (reported with 2σ errors). We note that some of the samples lack replicates from each season (labelled as ‘NA’) because there was insufficient BaSO4 to measure δ18O(SO4) (ref. 21).
To distinguish between atmospheric and rock sources of dissolved carbon, we measured DI13C and DIC concentrations at the Centre de Recherche Pétrographiques et Géochimiques and DI14C at the Laboratory for Ion Beam Physics at the ETH Zürich. For δ13C measurements, the samples and H3PO4 were put into glass vials and vaporized. The isotopic composition of the dissolved inorganic carbon within the remaining CO2 gas was measured with a Thermo Fisher EAlsolink-Delta V isotope ratio mass spectrometer. The DIC concentrations were estimated relative to a pure, synthetic calcite internal standard. We assumed conservative errors of 10% on the DIC calculations due to differences in the volume of air within the sampling tubes between liquid and solid samples (estimated to be 5%). The δ14C samples were prepared by purging 6 ml aliquots of each water sample with helium, acidifying the sample with 150 μl of 85% H3PO4 and heating the sample to 60 °C for 2 hours. We measured δ14C from the CO2 gas that formed from this process using an online carbonate handling system, which was connected to a mini carbon accelerator mass spectrometer (MICADAS AMS) equipped with a gas-accepting ion source.
Weathering reactions: theoretical expectations
We assume silicate and carbonate compositions equivalent to the generic endmembers normalized by Σ+ (refs. 37,21) and converted to units of mol/mol.
Within this framework, we constrain endmember compositions for carbonic acid (H2CO3) and sulfuric acid (H2SO4) weathering of carbonate and silicate rock (Fig. 2 and equations (1)−(4)).
The weathering reactions in equations (1)–(4) also produce different theoretical DIC signatures52 that reflect modern carbon sources (for example, biogenic carbon or atmospheric carbon from meteoric water) and rock-derived, radiocarbon dead carbon sources (for example, rock and metamorphic carbon). The H2CO3 weathering of carbonate contributes 1 mole of modern carbon and 1 mole of rock-derived carbon to the solvent (water), so the expected fraction modern carbon (F14C) is 0.5, whereas silicate weathering by H2CO3 contributes only modern carbon and thus has an expected F14C signature of 1. Similarly, weathering 1 mole of carbonate minerals by H2SO4 contributes only rock-derived carbon (F14C = 0), whereas silicate weathering by H2SO4 produces no alkalinity or DIC since the reaction does not include any carbon species (equation (3)).
These theoretical expectations do not account for the dissolution of evaporites (for example, halite and gypsum). In the Tevere River, some spring and proximal river samples illustrate [Na+] that are higher than [Ca2+]. All other samples illustrate higher [Ca2+] than [Na+], even for samples derived from siliciclastic-rich turbidites. Assuming that all SO42− and Cl− are derived from evaporite and balancing the cations, virtually all of the Na+ would be removed from solution for halite, but 7−98% of Ca2+ would be removed. Thus, correcting the samples for evaporite dissolution would have the overall effect of increasing Ca/Σ+ and decreasing SO4/Σ+.
Elemental and isotope corrections for degassing and secondary carbonate precipitation
Elemental corrections for secondary carbonate precipitation
Secondary carbonate precipitation enriches the remaining fluid with Sr2+ so that Sr2+/Ca2+ increases. We can express the final Sr2+/Ca2+ ratio of the fluid relative to the initial ratio of Sr2+ to Ca2+ \(\left(\frac{{\left[{{{\mathrm{Sr}}}}^{2+}\right]}_{0}}{{\left[{{{\mathrm{Ca}}}}^{2+}\right]}_{0}}\right)\), which reflects the absence of secondary precipitation:
Here, kd is the partition coefficient for Sr2+, and \({\gamma }_{{{\mathrm{CaC}}}{{\mathrm{O}}}_{3}}\) is the fraction of primary calcite that remains in the fluid53. The \({\gamma }_{{{\mathrm{CaC}}}{{\mathrm{O}}}_{3}}\) can range from 0 to 1, where a value of 1 reflects no loss of primary carbonate, and a value of 0 would theoretically indicate that all primary carbonate has been lost to secondary precipitation. We constrained \(\frac{{\left[{{{\mathrm{Sr}}}}^{2+}\right]}_{0}}{{\left[{{{\mathrm{Ca}}}}^{2+}\right]}_{0}}\) from bedrock ratios in generic silicate and carbonate bedrock compositions54, which form an endmember mixing line expressed by:
where a and b are the intercept and slope of the fit, respectively. The amount of secondary carbonate precipitation is then calculated as the deviation of the solute samples from the bedrock mixing line. We can solve for \(\frac{{\left[{{{\mathrm{Sr}}}}^{2+}\right]}_{0}}{{\left[{{{\mathrm{Ca}}}}^{2+}\right]}_{0}}\) by rearranging equation (5):
Assuming the concentration of Na+ does not change due to secondary carbonate precipitation, we can express the initial ratio of Sr2+/Ca2+ in terms of the Na+/Ca2+ ratio:
where \(\frac{{\left[{{{\mathrm{Na}}}}^{+}\right]}_{0}}{{\left[{{{\mathrm{Ca}}}}^{2+}\right]}_{0}}=\frac{\left[{{{\mathrm{Na}}}}^{+}\right]}{\left[{{{\mathrm{Ca}}}}^{2+}\right]}\)
We then combine equations (7) and (8) and solve for \({\gamma }_{{{\mathrm{CaC}}}{{\mathrm{O}}}_{3}}\) numerically:
We corrected for secondary precipitation with a partition coefficient of k = 0.05, which is within the acceptable range of values for k (0.02–0.20) (refs. 55,56,57).
Isotope fractionation due to CO2 degassing and secondary carbonate precipitation
Fractionation of bicarbonate in water happens during degassing of CO2 and during precipitation of CaCO3. We assess the effect of CO2 degassing and secondary carbonate precipitation on measured DIC and Ca2+ concentrations and on DI13C isotopic signatures. Reporting 14C as fraction modern (F14C) already accounts for fractionation that occurs in nature58, so we do not correct these values.
Degassing will preferentially result in the loss of more depleted carbon, thus enriching the remaining fluid, whereas precipitation of carbonate will result in the loss of heavier (more enriched) carbon. To correct for CO2 degassing and secondary precipitation, we use fractionation and enrichment factors that describe how carbon isotopes are fractionated due to individual processes21. Following the methodology of ref. 59, we assume (1) that CO2 degassing and secondary precipitation are irreversible reactions within an open system13 and (2) that half of the enrichment is due to degassing and half is due to precipitation, so that carbon is equally distributed between the two reactions. The carbon isotopic signature is expressed as ratio R (for example, 13C/12C) where the heavier isotope is the numerator. The fractionation of R is expressed as a ratio between different states, where A refers to the final state and B refers to the initial state:
The enrichment factor for the fractionation of phase A and B is commonly expressed in permil (‰), and can be calculated in relation to the fractionation factor α:
When αA–B > 1 or εA–B > 0, phase A becomes enriched (heavier) during fractionation, whereas the phase A will become depleted (lighter) during fractionation if αA–B < 1 or εA–B < 0.
The final isotopic composition of phase B (in ‰) after fractionation \(({\delta }_{{{\mathrm{B}}}_{{{\mathrm{final}}}}})\) can be related to the initial composition of phase B \(({\delta }_{{{\mathrm{B}}}_{{{\mathrm{initial}}}}})\), using the approximation of ref. 60:
where \({f}_{{\mathrm{B}}}\) is the fraction of the material B that remains after fractionation. Once we calculate the fractionation factors due to degassing and carbonate precipitation21, we can then combine the fractionation factor from both reactions as follows:
The enrichment factor for CO2 degassing is expressed as \({\varepsilon }_{{{{\mathrm{CO}}}}_{2}({\mathrm{g}})-{{{\mathrm{HCO}}}}_{3}}\), so the isotopic signature of HCO3 after reaction 1 \(\left({\delta }_{{{{{\mathrm{HCO}}}}_{3}}_{{{\mathrm{Step}}}1}}\right)\) can be expressed as:
In equation (14), the enrichment factor is divided by two since we assume that half of the total enrichment occurs with reaction 1 and the other half occurs with reaction 2 (equation (15)). The enrichment factor for carbonate precipitation is expressed as \({\varepsilon }_{{{{\mathrm{CaCO}}}}_{3}-{{{\mathrm{HCO}}}}_{3}}\), so the isotopic signature of HCO3 after reaction 2 \(\left({\delta }_{{{{{\mathrm{HCO}}}}_{3}}_{{{\mathrm{Step}}}2}}\right)\) is then:
We then combine equations (14) and (15) to calculate the enrichment factor that encompasses the full set of reactions:
where
We calculate \({\alpha }_{{{{\mathrm{CaCO}}}}_{3}-{{{\mathrm{HCO}}}}_{3}}\) (equation (18)) and convert it to an enrichment factor, given the relationship between fractionation and enrichment factors in equation (11).
Enrichment factors are temperature dependent, so we calculated separate enrichment factors for the winter and summer samples using the seasonal range of temperatures from cold springs in the central Apennines21,29.
To estimate \({f}_{{\mathrm{B}}}\), we calculate the fraction of DIC lost due to CO2 degassing associated with secondary carbonate precipitation (γDIC). Some CO2 degassing controlled by diffusion may also occur in the absence of carbonate precipitation41, although we have no way to estimate the magnitude of this process. However, previous studies suggest that the effect of diffusion-controlled degassing is negligible on isotope fractionation between gaseous CO2 (CO2(g)) and CO2 dissolved in water (CO2(aq)) because the reservoir of CO2(aq) in solution is small between pH of 6 and 9, and the isotope fractionation between CO2(g) and CO2(aq) is small at 25 °C (ref. 61). By contrast, degassing caused by secondary carbonate precipitation produces a large fractionation between CO2(g) and HCO3− at ambient temperatures62.
Thus, we first calculate the amount of HCO3− lost due to secondary carbonate precipitation (equations (3)−(9)). For each mol Ca2+ lost due to secondary carbonate precipitation, we lose 2 mol HCO3− so that the concentration of HCO3− before secondary precipitation can be expressed as:
where \({\left[{{{\mathrm{Ca}}}}^{2+}\right]}_{{{\mathrm{Final}}}}\) is the measured concentration of Ca in our water samples, and the initial concentration of Ca2+ before secondary carbonate precipitation \(\left({\left[{{{\mathrm{Ca}}}}^{2+}\right]}_{{{\mathrm{Initial}}}}\right)\) is:
The initial DIC concentration \({\left[{{\mathrm{DIC}}}\right]}_{{{\mathrm{Initial}}}}\) can then be expressed as the sum of the measured DIC concentration \({\left[{{\mathrm{DIC}}}\right]}_{{{\mathrm{Final}}}}\) and \({\left[{{{\mathrm{HCO}}}}_{3}^{-}\right]}_{{{\mathrm{Initial}}}}\), so that the fraction of DIC lost due to secondary precipitation \(\left({\gamma }_{{{\mathrm{DIC}}}}\right)\) can be expressed as:
Given the assumption that diffusion-controlled degassing should be negligible, we use \({\gamma }_{{{\mathrm{DIC}}}}\) as an approximation of \({f}_{{\mathrm{B}}}\).
MEANDIR model
Scenario parameters
Scenario parameters for the inversion with MEANDIR are given in ref. 21 and details about the endmember compositions in Supplementary Text 2–4. Here we normalize all endmembers to the sum of measured concentrations (in μmol l–1) of riverine Ca2+, Mg2+, Na+, SO42− and DIC (equation (21)):
where \(\chi\) designates the number of moles. Pyrite oxidation does not source any cations, although it is a source of SO42− and a sink of alkalinity, so we include SO42− in the normalization and treat the pyrite oxidation endmember independently of any weathering lithology37. Including DIC in the normalization also allows us to represent carbon endmembers that are decoupled from the weathering of lithologic endmembers.
Each variable is normalized by the sum of major dissolved cations given in equation (21) and is expressed in milliequivalents (mEq). To assure that the sum of variable ratios equals 1 and to maintain internal consistency for each endmember (equation (22)), we calculate the most abundant ratio through mass balance37.
For the DIC endmember, we assume DIC is sourced exclusively from biogenic carbon, metamorphic carbon, atmospheric carbon, cyclic inputs and carbonates. We calculate the DIC contribution for cyclic inputs and carbonate through charge balance and then convert the molar contributions to units of mEq. For the biogenic carbon endmember, we select a broad range of isotopic signatures for C3 plants that are dominant in central Italy63 and account for the enrichment of δ13C due to plant degradation. DO13C estimates for the Tyrrhenian side of the Apennines are not available, although the importance of C4 crops such as maize within the Tevere catchment64 would suggest that waters may have more enriched isotopic signatures relative to those of C3 plants.
Inversion approach
We invert all 100 samples for which we have all the required elemental and isotopic measurements. To select successful runs, we employ two separate criteria. First, we select from 1 × 106 simulations those with reconstructed chemical compositions that fall within prescribed misfit ranges (the ‘iterate over samples’ approach in MEANDIR). The final value and uncertainty are then calculated as the median and interquartile range of all accepted simulations. For all ion data, we allow reconstructed value within 75–125% of the observations21. For δ34S and δ13C isotopes, we allow a maximum misfit of ±2‰ and a misfit smaller than or equal to 0.05 for F14C (ref. 21). Given these bounds, 41% of winter samples and 57% of summer samples produce successful simulations (Supplementary Text 5). Other samples have misfits that are greater than the acceptable limits (Supplementary Text 5 and Supplementary Fig. 3)21. Second, we follow previous approaches of inversion models38,65 and select the best 5% of simulations to calculate the inversion result from 1 × 104 simulations. This approach produces successful inversions for all samples. From all 5% of accepted simulations, we calculate minimum and maximum misfit values21.
In all figures we present data from the inversions that fit within the prescribed misfit bounds (those samples with successes under the iterate-over-samples approach). These results represent the most conservative treatment of the inversion because it requires successful iterations to reproduce the observations within some misfit bounds. In the supplement, we provide the MEANDIR model fractional output using the selection of the top 5% of simulations21 and an alternative to summary Fig. 4 (Extended Data Fig. 6) that includes the full sample set (samples with successes using the iterate-over-samples approach and the results from the iterate-over-endmembers approach for the remaining samples).
Model outputs and calculations
The fractional contribution from each endmember is expressed as the median value from all accepted simulations, which we convert to concentrations, to compare results from all sampling locations and different spatial scales. To estimate inorganic CO2 consumption and production, we calculate the concentration of CO2 (in μmol l–1) that is sequestered or released from weathering. For silicate weathering, the consumed CO2 concentration \({\left[{{{\mathrm{CO}}}}_{2}\right]}_{{{\mathrm{Sil}}}}\) is calculated by assuming that each charge-equivalent ion sequesters 0.5 mol CO2 (refs. 38,65), such that
For metamorphic CO2 release \({\left[{{{\mathrm{CO}}}}_{2}\right]}_{{{\mathrm{Meta}}}}\), every charge equivalent of metamorphic DIC \(\left({\left[{{\mathrm{DIC}}}\right]}_{{{\mathrm{Meta}}}}\right)\) acts as a source for one mol CO2 to the atmosphere.
For pyrite oxidation \({\left[{{{\mathrm{CO}}}}_{2}\right]}_{{{\mathrm{Pyr}}}}\), we consider each charge equivalent of SO42− as a source of 0.5 mol CO2 because of the alkalinity consumption by sulfuric acid.
We do not include K+ in our unmixing model or calculations because its inclusion reduces the number of successful runs in the MEANDIR model by more than 50% without substantially affecting the estimates of weathering and carbon sources.
Where discharge measurements were available from the regional hydrologic authorities21, we divided these measurements by the upstream drainage area to calculate run-off and converted the CO2 concentrations into fluxes, expressed in tons of carbon (tC km–2 yr–1) (ref. 21). Daily discharge estimates were averaged over the two summer (July–August) or winter (March–April) months during which we sampled.
Data availability
The datasets used in this paper are available from https://doi.org/10.5880/GFZ.4.6.2024.001 (ref. 21) and https://doi.org/10.13127/class.1.0 (earthquake data)49.
Code availability
The MEANDIR model and user guide3 are available at https://github.com/PrestonCosslettKemeny/MEANDIR.
References
Kerrick, D. M. & Caldeira, K. Metamorphic CO2 degassing from orogenic belts. Chem. Geol. 145, 213–232 (1998).
Hilton, R. G. & West, A. J. Mountains, erosion and the carbon cycle. Nat. Rev. Earth Environ. 1, 284–299 (2020).
Larsen, I. J., Montgomery, D. R. & Greenberg, H. M. The contribution of mountains to global denudation. Geology 42, 527–530 (2014).
Raymo, M. E. & Ruddiman, W. F. Tectonic forcing of late Cenozoic climate. Nature 359, 117–122 (1992).
Maffre, P. et al. Mountain ranges, climate and weathering. Do orogens strengthen or weaken the silicate weathering carbon sink? Earth Planet. Sci. Lett. 493, 174–185 (2018).
Mörner, N.-A. & Etiope, G. Carbon degassing from the lithosphere. Glob. Planet. Change 33, 185–203 (2002).
Touret, J. L. R. CO2 transfer between the upper mantle and the atmosphere: temporary storage in the lower continental crust. Terra Nova 4, 87–98 (1992).
Frezzotti, M. L., Peccerillo, A. & Panza, G. Carbonate metasomatism and CO2 lithosphere–asthenosphere degassing beneath the western Mediterranean: an integrated model arising from petrological and geophysical data. Chem. Geol. 262, 108–120 (2009).
Urey, H. C. On the early chemical history of the Earth and the origin of life. Proc. Natl Acad. Sci. USA 38, 351–363 (1952).
Guo, Z., Wilson, M., Dingwell, D. B. & Liu, J. India–Asia collision as a driver of atmospheric CO2 in the Cenozoic. Nat. Commun. 12, 3891 (2021).
Sternai, P. et al. Magmatic forcing of Cenozoic climate? J. Geophys. Res. Solid Earth 125, e2018JB016460 (2020).
Menzies, C. D. et al. Carbon dioxide generation and drawdown during active orogenesis of siliciclastic rocks in the Southern Alps, New Zealand. Earth Planet. Sci. Lett. 481, 305–315 (2018).
Evans, M. J., Derry, L. A. & France‐Lanord, C. Degassing of metamorphic carbon dioxide from the Nepal Himalaya. Geochem. Geophys. Geosyst. 9, Q04021 (2008).
Becker, J. A., Bickle, M. J., Galy, A. & Holland, T. J. B. Himalayan metamorphic CO2 fluxes: quantitative constraints from hydrothermal springs. Earth Planet. Sci. Lett. 265, 616–629 (2008).
Cosentino, D., Cipollari, P., Marsili, P. & Scrocca, D. Geology of the central Apennines: a regional review. J. Virtual Explor. https://doi.org/10.3809/jvirtex.2010.00223 (2010).
Cavinato, G. P. & De Celles, P. G. Extensional basins in the tectonically bimodal central Apennines fold-thrust belt, Italy: response to corner flow above a subducting slab in retrograde motion. Geology 27, 955–958 (1999).
della Vedova, B., Bellani, S., Pellis, G. & Squarci, P. in Anatomy of an Orogen: The Apennines and Adjacent Mediterranean Basins (eds Vai, G. B. & Martini, I. P.) 65–76 (Kluwer Academic Publishers, 2001).
Piana Agostinetti, N. & Amato, A. Moho depth and Vp/Vs ratio in peninsular Italy from teleseismic receiver functions. J. Geophys. Res. Solid Earth 114, B06303 (2009).
Chiarabba, C. & Chiodini, G. Continental delamination and mantle dynamics drive topography, extension and fluid discharge in the Apennines. Geology 41, 715–718 (2013).
Faccenna, C., Becker, T. W., Miller, M. S., Serpelloni, E. & Willett, S. D. Isostasy, dynamic topography, and the elevation of the Apennines of Italy. Earth Planet. Sci. Lett. 407, 163–174 (2014).
Erlanger, E. et al. Sample information, major element stream chemistry, inversion model setup and results, sample corrections for precipitation and degassing, and CO2 exchange calculations. GFZ Data Services https://doi.org/10.5880/GFZ.4.6.2024.001 (2024).
Bigi, G. et al. Structural Model of Italy Sheet 3, 1:500,000 (C.N.R., Progretto Finalizzato Geodinamica, SELCA, 1992).
Bigi, G. et al. Structural Model of Italy Sheet 4, 1: 500,000 (C.N.R., Progretto Finalizzato Geodinamica, SELCA, 1992).
Calmels, D., Gaillardet, J., Brenot, A. & France-Lanord, C. Sustained sulfide oxidation by physical erosion processes in the Mackenzie River basin: climatic perspectives. Geology 35, 1003–1006 (2007).
D’Angeli, I. M. et al. Sulfuric acid caves of Italy: a review. Geomorphology 333, 105–122 (2019).
Frondini, F. Geochemistry of regional aquifer systems hosted by carbonate-evaporite formations in Umbria and southern Tuscany (central Italy). Appl. Geochem. 23, 2091–2104 (2008).
Chiodini, G. et al. Correlation between tectonic CO2 Earth degassing and seismicity is revealed by a 10-year record in the Apennines, Italy. Sci. Adv. 6, eabc2938 (2020).
Minissale, A. Origin, transport and discharge of CO2 in central Italy. Earth Sci. Rev. 66, 89–141 (2004).
Chiodini, G., Frondini, F., Cardellini, C., Parello, F. & Peruzzi, L. Rate of diffuse carbon dioxide Earth degassing estimated from carbon balance of regional aquifers: the case of central Apennine, Italy. J. Geophys. Res. Solid Earth 105, 8423–8434 (2000).
Ascione, A. et al. Assessing mantle versus crustal sources for non-volcanic degassing along fault zones in the actively extending southern Apennines mountain belt (Italy). GSA Bull. 130, 1697–1722 (2018).
Di Luccio, F. et al. Geodynamics, geophysical and geochemical observations, and the role of CO2 degassing in the Apennines. Earth Sci. Rev. 234, 104236 (2022).
Roberts, G. P. & Michetti, A. M. Spatial and temporal variations in growth rates along active normal fault systems: an example from The Lazio–Abruzzo Apennines, central Italy. J. Struct. Geol. 26, 339–376 (2004).
Cosentino, D. et al. New insights into the onset and evolution of the central Apennine extensional intermontane basins based on the tectonically active L’Aquila Basin (central Italy). GSA Bull. 129, 1314–1336 (2017).
Ghisetti, F. & Vezzani, L. Normal faulting, transcrustal permeability and seismogenesis in the Apennines (Italy). Tectonophysics 348, 155–168 (2002).
Chiodini, G. et al. Quantification of deep CO2 fluxes from central Italy. Examples of carbon balance for regional aquifers and of soil diffuse degassing. Chem. Geol. 159, 205–222 (1999).
Rogie, J. D., Kerrick, D. M., Chiodini, G. & Frondini, F. Flux measurements of nonvolcanic CO2 emission from some vents in central Italy. J. Geophys. Res. Solid Earth 105, 8435–8445 (2000).
Kemeny, P. C. & Torres, M. A. Presentation and applications of mixing elements and dissolved isotopes in rivers (MEANDIR), a customizable MATLAB model for Monte Carlo inversion of dissolved river chemistry. Am. J. Sci. 321, 579–642 (2021).
Bufe, A. et al. Co-variation of silicate, carbonate and sulfide weathering drives CO2 release with erosion. Nat. Geosci. 14, 211–216 (2021).
Berner, E. K. & Berner, R. A. Global Environment: Water, Air, and Geochemical Cycles (Princeton Univ. Press, 2012).
Crespi, A., Brunetti, M., Lentini, G. & Maugeri, M. 1961–1990 high-resolution monthly precipitation climatologies for Italy. Int. J. Climatol. 38, 878–895 (2018).
Dreybrodt, W. Physics and chemistry of CO2 outgassing from a solution precipitating calcite to a speleothem: implication to 13C, 18O, and clumped 13C18O isotope composition in DIC and calcite. Acta Carsologica 48, 59–68 (2019).
Calmels, D. et al. Contribution of deep groundwater to the weathering budget in a rapidly eroding mountain belt, Taiwan. Earth Planet. Sci. Lett. 303, 48–58 (2011).
Ramondenc, S. et al. An initial carbon export assessment in the Mediterranean Sea based on drifting sediment traps and the underwater vision profiler data sets. Deep-Sea Res. I: Oceanogr. Res. Pap. 117, 107–119 (2016).
Galy, V., Peucker-Ehrenbrink, B. & Eglinton, T. Global carbon export from the terrestrial biosphere controlled by erosion. Nature 521, 204–207 (2015).
Torres, M. A., West, A. J. & Li, G. Sulphide oxidation and carbonate dissolution as a source of CO2 over geological timescales. Nature 507, 346–349 (2014).
Spada, M., Bianchi, I., Kissling, E., Agostinetti, N. P. & Wiemer, S. Combining controlled-source seismology and receiver function information to derive 3-D moho topography for Italy. Geophys. J. Int. 194, 1050–1068 (2013).
Devoti, R., Esposito, A., Pietrantonio, G., Pisani, A. R. & Riguzzi, F. Evidence of large scale deformation patterns from GPS data in the Italian subduction boundary. Earth Planet. Sci. Lett. 311, 230–241 (2011).
Latorre, D., Di Stefano, R., Castello, B., Michele, M. & Chiaraluce, L. An updated view of the Italian seismicity from probabilistic location in 3D velocity models: the 1981–2018 Italian catalog of absolute earthquake locations (CLASS). Tectonophysics 846, 229664 (2023).
Latorre, D., Di Stefano, R., Castello, B., Michele, M. & Chiaraluce, L. Catalogo delle Localizzazioni ASSolute (CLASS): Locations Version 1 (INGV, 2022).
Paris, G., Sessions, A. L., Subhas, A. V. & Adkins, J. F. MC-ICP-MS measurement of δ34S and ∆33 S in small amounts of dissolved sulfate. Chem. Geol. 345, 50–61 (2013).
Ding, T. et al. Calibrated sulfur isotope abundance ratios of three IAEA sulfur isotope reference materials and V-CDT with a reassessment of the atomic weight of sulfur. Geochim. Cosmochim. Acta 65, 2433–2437 (2001).
Blattmann, T. M. et al. Sulphuric acid-mediated weathering on Taiwan buffers geological atmospheric carbon sinks. Sci. Rep. 9, 2945 (2019).
Bickle, M. J., Tipper, E., Galy, A., Chapman, H. & Harris, N. On discrimination between carbonate and silicate inputs to Himalayan rivers. Am. J. Sci. 315, 120–166 (2015).
Gaillardet, J., Dupré, B. & Louvat, P. Global silicate weathering and CO2 consumption rates deduced from the chemistry of large rivers. Chem. Geol. 159, 3–30 (1999).
Nehrke, G., Reichart, G.-J., Van Cappellen, P., Meile, C. & Bijma, J. Dependence of calcite growth rate and Sr partitioning on solution stoichiometry: non-Kossel crystal growth. Geochim. Cosmochim. Acta 71, 2240–2249 (2007).
Gabitov, R. I. & Watson, E. B. Partitioning of strontium between calcite and fluid. Geochem. Geophys. Geosyst. https://doi.org/10.1029/2005GC001216 (2006).
Tesoriero, A. J. & Pankow, J. F. Solid solution partitioning of Sr2+, Ba2+, and Cd2+ to calcite. Geochim. Cosmochim. Acta 60, 1053–1063 (1996).
Fahrni, S. M. et al. Reassessment of the 13C/12C and 14C/12C isotopic fractionation ratio and its impact on high-precision radiocarbon dating. Geochim. Cosmochim. Acta 213, 330–345 (2017).
Hayes, J. M. Fractionation of carbon and hydrogen isotopes in biosynthetic processes. Rev. Mineral. Geochem. 43, 225–277 (2001).
Mariotti, A. et al. Experimental determination of nitrogen kinetic isotope fractionation: some principles; illustration for the denitrification and nitrification processes. Plant Soil 62, 413–430 (1981).
Vogel, J. C., Grootes, P. M. & Mook, W. G. Isotopic fractionation between gaseous and dissolved carbon dioxide. Z. Phys. A 230, 225–238 (1970).
Yan, H., Liu, Z. & Sun, H. Large degrees of carbon isotope disequilibrium during precipitation-associated degassing of CO2 in a mountain stream. Geochim. Cosmochim. Acta 273, 244–256 (2020).
Quade, T. C. J. in Climate Change in Continental Isotopic Records (eds Swart, P. K. et al.) 217–231 (AGU, 1993).
Fanfarillo, E., Kasperski, A., Giuliani, A. & Abbate, G. Shifts of arable plant communities after agricultural intensification: a floristic and ecological diachronic analysis in maize fields of Latium (central Italy). Bot. Lett. 166, 356–365 (2019).
Torres, M. A. et al. The acid and alkalinity budgets of weathering in the Andes–Amazon system: insights into the erosional control of global biogeochemical cycles. Earth Planet. Sci. Lett. 450, 381–391 (2016).
Acknowledgements
We thank T. Rigaudier, O. Rach, T. Goldberg and C. Zimmermann for analysing our water chemistry samples; D. Benedini for his help with collecting samples in the field; and S. Gallen and J. Rugenstein for their input and discussions. We also thank the Regione Abruzzo-Servizio Idrografico Mareografico; the Regione Umbria-Servizio Rischio idrogeologico, idraulico e sismico, difesa del suolo; and the Centro Funzionale della Regione Lazio for providing discharge information. This project was funded by an SNF Early Postdoc Mobility Fellowship (P2EZP2_187993) and a Europlanet 2024 Research Infrastructure Grant (20-EPN2-014). P.C.K. acknowledges support through NSF-EAR (award #2204376) and through the TC Chamberlin Fellowship at UChicago.
Funding
Open access funding provided by Helmholtz-Zentrum Potsdam Deutsches GeoForschungsZentrum - GFZ.
Author information
Authors and Affiliations
Contributions
E.E., A.B. and N. Hovius conceived the study; E.E., A.B., G.P., I.D., L.P., J.S. and N. Haghipour contributed samples and laboratory analyses; E.E. led the data analysis with contributions from A.B. and P.C.K.; and all authors contributed to the writing and editing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Geoscience thanks Catriona Menzies and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Alireza Bahadori and Tamara Goldin, in collaboration with the Nature Geoscience team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Location map with numbered sampling locations.
Stream networks for the studied rivers are shown in blue, and adjacent stream networks are shown in black. Layers are overlain on a Shuttle Radar Topography Mission (SRTM) 90-m hillshade and digital elevation model (DEM).
Extended Data Fig. 2 Endmember mixing models for sulfur, oxygen, and carbon isotopic signatures.
δ18O(SO42−) plotted against δ34S for (a) winter samples and (b) summer samples. Ternary diagram illustrating the proportion of measured DIC, SO42−, and Ca2+ concentrations relative to endmember weathering acids for (c) winter samples and (d) summer samples. River samples are colored by the measured δ34S signature. (a, b) Samples are colored by surface lithology (carbonate, mixed, and siliciclastic) and by catchment (Aterno-Pescara or Tevere River). River and spring samples are illustrated as circle and x symbols, respectively, and the numbered springs correspond with sampling locations given in ref. 21. Endmember isotopic signatures for pyrite and evaporites are given in ref. 21.
Extended Data Fig. 3 CO2 sinks and sources (winter samples) illustrated in concentration units.
CO2 exchange with the atmosphere is attributed to (a) and (b) silicate weathering, (c) and (d) pyrite oxidation, and (e) and (f) metamorphic carbon for sampling locations along the Tevere River (left column) and the Aterno-Pescara River (right column). Data bars represent sample mean values ± 1σ (ref. 21).
Extended Data Fig. 4 CO2 sinks and sources (summer samples) illustrated in concentration units.
CO2 exchange with the atmosphere is attributed to (a) and (b) silicate weathering, (c) and (d) pyrite oxidation, and (e) and (f) metamorphic carbon for sampling locations along the Tevere River (left column) and the Aterno-Pescara River (right column). Data bars represent sample mean values ± 1σ (ref. 21).
Extended Data Fig. 5 CO2 sinks and sources inferred from the Tevere and Aterno Pescara River chemistry for all locations with successful MEANDIR runs using the ‘iterate over samples’ approach and available discharge measurements.
CO2 exchange with the atmosphere is shown as fluxes associated with mechanisms that result in long-term CO2 drawdown (silicate weathering) or CO2 release (pyrite oxidation and metamorphic carbon). The sum of the fluxes is illustrated as the total CO2 exchange with the atmosphere. Data bars represent mean values ± 1σ (ref. 21). Note that the fluxes from L’Aquila are shown to illustrate the dominate flux patterns, although the fluxes themselves are on the order of 1e−6 and are thus negligible.
Extended Data Fig. 6 Overview of the regional geodynamic setting in relation to the full set of metamorphic CO2 results from both the ‘iterate over samples’ and ‘iterate over endmembers’ model approaches.
a) and b) Colored circles and squares illustrate samples with non-zero yearly average HCO3 from metamorphic carbon, scaled by the concentration. White, outlined circles and squares illustrate samples where HCO3 from metamorphic CO2 is zero (ref. 21). The purple line marks the boundary between low p-wave velocity (Vp) anomalies to the west and high Vp anomalies to the east at 52 km depth, and the dashed indentations in the line mark the locations of slab windows in the central (CAW) and southern Apennines (SAW). The orange overlay illustrates the spatial extent of measured CO2 gas emissions, gray circles illustrate the locations and depth of seismicity deeper than 40 km and magnitude 3 or higher, and the black sawtoothed line marks the subduction front. b) illustrates an enlarged view of the results within the study area, including the locations of normal faults (black lines). Figure adapted with permission from refs. 8,47,48 Elsevier.
Supplementary information
Supplementary Information
Supplementary Fig. 1 and Text.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Erlanger, E., Bufe, A., Paris, G. et al. Deep CO2 release and the carbon budget of the central Apennines modulated by geodynamics. Nat. Geosci. 17, 465–471 (2024). https://doi.org/10.1038/s41561-024-01396-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41561-024-01396-3