Abstract
The extent of grounded ice and buttressing by the Ronne Ice Shelf, which provides resistance to the outflow of ice streams, moderate West Antarctic Ice Sheet stability. During the Last Glacial Maximum, the ice sheet advanced and was grounded near the Weddell Sea continental shelf break. The timing of subsequent ice sheet retreat and the relative roles of ice shelf buttressing and grounding line changes remain unresolved. Here we use an ice core record from grounded ice at Skytrain Ice Rise to constrain the timing and speed of early Holocene ice sheet retreat. Measured δ18O and total air content suggest that the surface elevation of Skytrain Ice Rise decreased by about 450 m between 8.2 and 8.0 kyr before 1950 ce (±0.13 kyr). We attribute this elevation change to dynamic thinning due to flow changes induced by the ungrounding of ice in the area. Ice core sodium concentrations suggest that the ice front of this ungrounded ice shelf then retreated about 270 km (±30 km) from 7.7 to 7.3 kyr before 1950 ce. These centennial-scale changes demonstrate how quickly ice mass can be lost from the West Antarctic Ice Sheet due to changes in grounded ice without extensive ice shelf calving. Our findings both support and temporally constrain ice sheet models that exhibit rapid ice loss in the Weddell Sea sector in the early Holocene.
Similar content being viewed by others
Main
Currently, 40–70% of Antarctic Bottom Water formation occurs in the Weddell Sea and the nine ice streams in the Weddell Sea Embayment (WSE; defined as 0° W to ~60° W) drain 22% of the Antarctic Ice Sheet’s grounded ice area1,2. The ice dynamics of the WSE are therefore an important control of sea level and thermohaline circulation3. The buttressing effect of the Ronne Ice Shelf, located at the edge of the Weddell Sea, plays a critical role in the stability of the West Antarctic Ice Sheet (WAIS)3. The WAIS is prone to instability and rapid grounding-line retreat because the ice is grounded below sea level and its bed deepens poleward3,4,5,6. Such retreat could, for example, be initiated by sub-ice-shelf melting due to ocean warming. Grounding-line retreat and reduced buttressing can result from ice thinning and ice shelf calving. The relative effect of these two processes on modern WAIS retreat is still an area of active research7,8.
Understanding past ice sheet elevation change and ice shelf calving and thinning in the WSE provides insight into how ice sheet stability in the region may change as the ocean continues to warm9. The understanding that the WSE deglaciated since the Last Glacial Maximum (LGM; ca. 23 to 19 kyr before present (BP) (defined as 1950 ce)) is well established, but the timing of retreat, which could help in determining how quickly the ice sheet could retreat in the future, is still debated10,11,12,13. This uncertainty is largely due to a scarcity of geological data pertaining to the glaciological history of the region3,6,11,14,15.
Ice sheet simulations and data syntheses provide a variety of reconstructions. They suggest that the ice sheet in the WSE possibly (1) did not retreat until later in deglaciation or possibly even until the Holocene10; (2) retreated and thinned rapidly for a few thousand years in the Holocene4,9,13,15; and/or (3) may have even re-advanced in the late Holocene11,16.
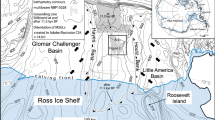
The timing of ice sheet change in the Holocene is not well resolved and was potentially not spatially uniform across the WSE4,14,15. In this Article, this ice sheet change is investigated using an ice core drilled at Skytrain Ice Rise (SIR). An ice rise is an area of grounded ice consisting of a separate flow centre within an ice shelf17,18. SIR is located north of the Ellsworth Mountains at the southern edge of the Ronne Ice Shelf (Fig. 1). In this study, the magnitude of rapid thinning at SIR and subsequent Ronne Ice Shelf retreat in the western part of the WSE is estimated. The timing of these events is constrained to periods of about 200 and 400 years in the early Holocene, respectively. These periods were identified using stable water isotope (δ18O), seasalt and total air content (TAC) records from the ice core drilled at SIR. This ice-core-derived history is compared with previously published Parallel Ice Sheet Model (PISM) predictions of the last deglaciation to demonstrate that the SIR data can quantitatively constrain ice sheet models12.
a,b, Regional map48 based on USGS Antarctic Overview map (a) and local map of the SIR developed using the Quantarctica mapping environment detailed in Matsuoka et al. (2021)49 (b). a, The red shading shows the locations9,15,42,43,44 of the cosmogenic exposure ages referred to in the text that are closest to SIR. b, The elevation shading is from the CryoSat-2 and RAMP2 elevation models, and the contour lines are at 500-m intervals from CryoSat-2 (ref. 49). The star shows the location of the drill site (b).
SIR δ 18O and TAC records
The SIR ice core δ18O record shows a major shift from −35.3‰ to −31.5‰ from 8.17 to 7.99 ka BP (Fig. 2). The rise of 3.9 ± 0.1‰ occurs in a span of 176 ± 43 years, diverging from an otherwise stable δ18O record, with only slight variability around the mean throughout the Holocene. After this increase, δ18O remained elevated to present.
a–c, Early Holocene Skytrain ice core δ18O (a), sodium (b) and TAC (c). Top and middle: dark-blue and dark-green lines show 20-year bin averages (a and b). The red lines are the linear fits of the δ18O and sodium records. The raw sodium data are truncated at higher values (Supplementary Fig. 3). The violet and grey bars are the early Holocene δ18O and sodium transitions, respectively. Bottom: the black line is the TAC record on the gas age scale (c). The red lines are the early and late Holocene means.
The strong present-day linear relationship between local temperature and surface snow δ18O is widely used to interpret temporal ice core δ18O variability as changes in temperature19. However, a similar abrupt shift is not present in global temperature reconstructions of the Holocene or in the WAIS Divide ice core δ18O record20,21,22. Global temperature reconstructions show an early Holocene optimum and cooling throughout the Holocene21,22. In West Antarctica, summer temperatures increased from the early Holocene to 4.1 kyr BP and then cooled to present20. Winter WAIS Divide ice core δ18O does drop briefly at about 8 kyr BP20, but it does not exhibit the dramatic increase that is then retained for the rest of the Holocene in the SIR ice core δ18O record.
Given the inconsistency between the δ18O signal at SIR and those at all other Antarctic sites, it is unlikely that the SIR abrupt shift is reflective of wider regional climatic change. We hypothesize that the SIR δ18O signal is controlled by local elevation change due to the surface lapse rate effect, which is the inverse relationship between temperature and ice sheet elevation that also affects ice core δ18O (refs. 19,20,23,24). As moist air travels higher in elevation, cools and condenses, more of the 18O is lost relative to 16O. This isotopic fractionation results in a change in δ18O in response to elevation at SIR, as measured in the ice core.
We therefore propose that the SIR δ18O increase centred at 8.1 kyr BP represents an abrupt elevation decrease of SIR to its present elevation. The δ18O transition is compared to observations and to isotope-enabled general circulation model results19,24,25 to investigate the magnitude of SIR elevation change that it could represent. Using relationships derived from spatial data and from isotope-enabled models (Methods), we estimate that the gradient of δ18O versus ice sheet elevation change applicable to SIR is 0.8 ± 0.2‰ per 100 m. This range implies that the elevation decrease at SIR in the early Holocene was probably between 390 m and 650 m, with the central value of the gradient suggesting an elevation decrease of 480 m.
The drop in elevation indicated by the δ18O record is supported by the SIR TAC data. Before the shift in water isotopes (from 9.5 to 8.5 kyr BP), TAC is relatively stable at 118.4 ± 1.4 ml kg−1 (±1σ). Following a complex oscillation, TAC stabilizes at levels of 125.0 ± 2.4 ml kg−1 from 6.6 to 5.0 kyr BP. The overall increase of 6.6 ml kg−1 equates to an elevation drop of 430 ± 110 m when the uncertainties in the temperature and pore volume at bubble closure are taken into account (Methods). This falls within the range, but at the lower end, of the isotope-based estimate.
The large swings in TAC from 8.0 to 7.0 kyr BP preclude an independent constraint on the timing of the elevation drop. In this section of the ice core, the signal is altered by large and poorly understood effects from the dynamical adjustment of the firn to rapid increases in both temperature and accumulation, and perhaps shear caused by changes in ice flow. Most ice core records of TAC come from sites that have not experienced large and sudden changes in elevation and thus the TAC signal is dominated by these other effects26,27, including those induced by orbital variations28. SIR is unique in that we have clear evidence of a rapid change in elevation that is directly supported by TAC. Further work may disentangle the firn response from the elevation effect, but, for now, we stress that the TAC data between 8.0 and 7.0 kyr BP cannot be interpreted as changes in elevation.
The SIR sodium record
SIR ice core sodium concentrations more than double from 26 to 59 μg kg−1 over a 600-year interval between 7.7 and 7.1 kyr BP. The main increase occurs over a 340 ± 80 year period centred at 7.5 kyr BP (Fig. 2). Ice core sodium is derived from seasalt aerosol sourced from the open ocean and the sea ice surface29,30,31 and is often interpreted as a proxy for sea ice extent32,33,34,35,36 and/or atmospheric circulation variability33. Other ions that are also sourced primarily from seasalt (chloride and magnesium) show the same feature at SIR in the early Holocene, mirroring the rapid increase in sodium.
The abrupt SIR sodium concentration increase is not observed in other Antarctic ice core sodium records, which exhibit a slight increase in sodium throughout the Holocene, especially between 10 and 8 kyr BP, attributed to circum-Antarctic wintertime sea ice expansion35. Given its abruptness, magnitude and absence in other Holocene ice core records, this sodium rise must be symptomatic of something more dramatic than a distant, gradual change in sea ice extent.
We note that the increase in sodium concentrations begins about 300 years after the δ18O increase has ended (Fig. 2). With such a large delay, a common hydrological cause37 can be ruled out. Furthermore, this lag suggests that the sodium decrease does not result from the site’s elevation decline. This is supported by comparisons of chemistry in shallow ice cores from Berkner Island and the ice shelf to its west, which show no change in seasalt concentration across a 900-m gradient in elevation38.
There is a direct relationship between sodium concentration and distance from the coast (that is, proximity to seasalt sources)39. The distance from SIR to the coast would change if the ice sheet or, more specifically, the Ronne Ice Shelf retreated. The magnitude of the possible retreat of the Ronne Ice Shelf in the early Holocene is estimated by comparison to a study40, in which major ions were measured in snow samples from a spatial transect stretching from the edge of the Ronne Ice Shelf towards the grounding line (Fig. 3). Because both chloride and sodium at this site are dominated by seasalt, we can convert chloride data from the transect40 to equivalent sodium concentrations using their ratio in seawater. The relationship between sodium concentration and distance is fit to an exponential function used to estimate the magnitude of ice shelf retreat (Methods). This analysis suggests that SIR was about 1,000 km from the edge of the Ronne Ice Shelf in the early Holocene. It then retreated about 270 ± 30 km between 7.7 and 7.3 kyr BP to 700 km, which is near its current position about 680 km from the ice edge.
Constraints on ice sheet retreat
Ice sheet model simulations estimate a period of WAIS retreat in the WSE between 13 and 5 kyr BP3,10,12. Several local palaeo-elevation studies show coincident WSE ice sheet thinning. Depending on the study location and proxy used, this period lasted between 3,000 and 8,000 years at varying time intervals3,4,9,11,15,41. Exposure age studies suggest that this thinning ranged from 200 to 800 m depending on the WSE site. These sites include the Ellsworth Mountains15, the Pensacola Mountains42,43,44, the southern Antarctic Peninsula45 and the Lassiter Coast9.
SIR is located between the Rutford and Institute Ice Streams, and is bordered by the Ellsworth Mountains to the south. The ice streams exceeded elevations of 1,300 m during the LGM4. Geomorphological and cosmogenic nuclide data from the Ellsworth Mountains suggest that ice thickness 100 km inland (west) of SIR decreased by ~400 m from ca. 6.5 to 3.5 kyr BP, similar in magnitude to the thinning shown in the SIR δ18O record, but slightly later (although with large chronological uncertainty)15. It was proposed that this period of thinning may have been due to grounding-line retreat into the Hercules Inlet that changed the direction of regional ice flow from southeastward towards the Institute Ice Stream to its present direction northward towards Horseshoe Glacier, directly south of SIR15.
Geological reconstructions4 suggesting fast but asynchronous thinning of the Institute and Rutford Ice Streams have been interpreted using a set of PISM simulations. A later version of the PISM model has also been used to investigate post-glacial retreat of the Antarctic Ice Sheet, including that in the WSE10,12. These predictions support an extensive early Holocene retreat of WAIS.
In this study, we used the PISM reference scenario (2205_LGM) from this later model version to extract surface elevation change at SIR at centennial-scale resolution to further understand this retreat at SIR12. We also estimated the distance from the ice core site to the grounding line and ice shelf edge along a transect that runs roughly perpendicular to the modern ice shelf edge (azimuth 65° from SIR). This simulation shows a rapid decrease (>2 m per year) in elevation at SIR of ~1,000 m starting around 12.5 kyr BP, followed by a gradual increase (~0.1 m per year) in elevation due to isostatic rebound (Fig. 4). In this simulation, preceding the drop in elevation, the grounding line first pulls back gradually (~0.3 km per year) over about 1,000 years. It then retreats rapidly (>1 km per year) to near its present-day position. This rapid retreat is coincident with the large drop in elevation. Once ice sheet thinning leads to the formation of a floating ice shelf, the ice shelf edge retreats in conjunction with the grounding line. The modelled minimum extent of the ice shelf edge is ~500 km from SIR. The ice shelf then re-advances to a position that is farther from SIR than the actual modern-day configuration. This bias continues to the present day in the model run.
a, Surface elevation (blue solid line) and bedrock elevation (blue dashed line) simulated using the PISM model12 and surface elevation calculated using SIR δ18O (pink) with 250-year box smoothing. The shading represents the range when using slopes of 0.8 ± 0.2‰ per 100 m as the conversion from δ18O to elevation. b, Rate of surface elevation change determined using PISM model (blue shading) and SIR δ18O (pink shading). The pink dashed lines show the rate calculated using the range of δ18O to elevation slopes. c, Grounding line (solid line) and ice shelf edge (dashed line) simulated using PISM model. Ice core data are plotted using the SIR age scale (top axis) and model results are plotted on the model timescale (bottom axis). The grey bar is the early Holocene transition, and the black dashed line is the inflection point of the transition.
The SIR isotope-derived estimate of the rate of elevation change and the model prediction show remarkable agreement (Fig. 4). The model and observations both show that SIR dropped by over 2 m per year in an event lasting just a few centuries. This is a direct confirmation of rapid ice sheet retreat. These results strongly support an inherently unstable WAIS in the WSE during the LGM that becomes rapidly ungrounded.
However, the overall magnitude of the drop simulated by PISM is larger than the ice core estimate. The simulated absolute timing of the drop also varies widely depending on various parameter choices, resolution and imposed bed topography. For example, a similar sequence of events is simulated in an updated and re-tuned version of PISM, but the timing of the elevation drop occurs around 6 kyr BP (not shown)10. Additionally, the simulated early ice shelf retreat and subsequent re-advance are not supported by the SIR sodium data. These discrepancies demonstrate how the SIR ice core data can be used to tune ice sheet models to improve the accuracy of simulated rapidity, timing and magnitude of ice sheet elevation change (and secondarily ice shelf extent) during the Holocene.
The SIR ice core δ18O and sodium records have the accuracy and resolution to reveal centennial-scale ice dynamical change in the WSE in the Holocene. Given the ice mass loss reported in the millennial-scale studies and PISM modelling, and the centennial-scale delay between the SIR ice core δ18O and sodium records, we propose the following sequence of events between 8.2 and 7.3 kyr BP: (1) while the Antarctic Ice Sheet may have become ungrounded farther north at an earlier date, ungrounding north of SIR occurred at ca. 8.2 kyr BP. The instability that resulted as grounded ice became floating ice shelf allowed SIR ice to flow faster and possibly in a different direction, leading to thinning over a short period of time of only 176 ± 43 years between 8.2 and 8.0 kyr BP. After this shift, SIR remained near its current elevation throughout the rest of the Holocene. (2) Within a few hundred years of this elevation change, the Ronne Ice Shelf edge then retreated between 7.7 and 7.3 kyr BP to near its current position. This retreat was far from SIR and apparently did not further affect SIR elevation (Fig. 5).
Broader implications for past and future retreat
This study shows that SIR can become unstable without extensive simultaneous ice shelf calving. Instability could instead have been driven by ice sheet thinning and ungrounding. This possibility is well aligned with Gudmundsson et al. (2019)8, which demonstrated, using a process-based model, that ice shelf thinning drives modern grounded ice mass loss. The subsequent ice shelf calving exhibited in the record also demonstrates that calving does not necessarily result in ice sheet instability in the WSE, at least as far inland as SIR. This idea of passive ice shelf calving was proposed in Furst et al. (2016)7. The retreat of the ice shelf edge was, however, coincident with abrupt thinning close to the ice shelf margin, at least at the Lassiter Coast9. This ice shelf weakening related to nearby rapid thinning on land is proposed in cosmogenic nuclide studies46,47.
Our result places a strong constraint on the timing of ice sheet retreat in the WSE. In the future this constraint could be supplemented by similar studies at other ice rises in the Ronne and Ross Ice Shelf regions, so as to place precise timings on other aspects of post-glacial WAIS retreat. Our results are also a direct demonstration of the speed at which ice mass can be lost when the grounding line of a marine-based ice sheet retreats. Our results suggest that the elevation at SIR reduced by an average of more than 2 m per year for two centuries.
Methods
Site characteristics and sample preparation
The ice core analysed in this study was drilled over a 3-month period from 2018 to 2019 on SIR (79° 44.46′ S, 78° 32.69′ W). At the time of drilling, the surface elevation of the site was 784 m above sea level and the ice was grounded 133 m above sea level. The site is directly south of the Ronne Ice Shelf and about 50 km north of the Ellsworth Mountains. It has a mean annual surface temperature of −26 °C. The ice core was drilled to the bedrock (651 m) using the British Antarctic Survey (BAS) intermediate depth drill and cut into 80-cm sections18,50.
Ice core analysis
The chemical components presented in this study were primarily measured using the BAS continuous flow analysis (CFA) system. A 3.2-cm × 3.2-cm inner cross-section of each 80-cm cylindrical ice core segment was used for CFA. This system is described in detail in Grieman et al. (2022)48.
Stable water isotope analysis
Stable water isotopes (H218O and HDO, defined relative to Vienna Standard Mean Ocean Water and Vienna Standard Light Antarctic Precipitation (VSMOW-VSLAP) as δ18O and δD, respectively) were measured continuously using a Picarro L2130-i cavity ring down spectrometer (CRDS; Supplementary Fig. 1). Melt water was directed via peristaltic pump from the continuous melter to the CRDS, where the sample was vapourized. The water vapour pressure of the sample inside the CRDS measurement cell was controlled using a manual needle valve attached to the outlet of the CRDS connected to a membrane vacuum pump. Using this valve, the water vapour pressure was maintained near 20,000 ppm (water vapour/ambient air) throughout the campaign. Samples of known isotopic composition from an ice core drilled at Berkner Island and modern ultrapure water samples previously analysed using isotope-ratio mass spectrometry were used for calibration.
Ice core δ18O and δD levels measured using CFA were compared with those measured in discrete samples (Supplementary Fig. 2). A Picarro L2130-i CRDS was used to measure δ18O and δD in discrete samples cut along the ice core from the discrete isotope strips 1 and 2 (ref. 48) as well as in 95 snow pit samples. The snow pit was sampled at 3 cm resolution along the topmost 2.85 m from the surface. A total of 2.2 μl of each sample was injected to maintain a water concentration of 18,000 ppm. Seven injections were made of each sample. To avoid carry-over, the data from the first three injections were discarded.
Seasalt analysis
Sodium and calcium were measured continuously using an Agilent 7700x inductively coupled plasma mass spectrometer. This analysis was validated using simultaneous Dionex ICS-3000 fast ion chromatography measurements (Supplementary Fig. 3). Calcium was also measured using a continuous fluorometry technique. These methods are compared and described in detail in Grieman et al. (2022)48. The inductively coupled plasma mass spectrometer measurements are presented in this study. The 43Ca isotope was used for calcium. Calcium was used in this study to determine the seasalt component of total sodium.
To understand how the sources of seasalt to SIR changed throughout the Holocene, the seasalt component of the sodium signal in the ice core needed to be determined. A method following35,37,51,52,53 was used to partition the sodium signal based on known crustal and marine ratios of calcium to sodium. The seasalt sodium (ssNa) component was determined using equation (1)
in which [Na] and [Ca] are the total measured concentrations of sodium and calcium, respectively, and Rm and Rt are the mean marine and terrestrial ratios of calcium to sodium of 0.038 and 1.78, respectively54. This calculation assumes that these marine and terrestrial ratios are correct and remained constant throughout the Holocene. Using this equation, the fraction of ssNa was determined to be 97% in the Holocene.
This percentage was defined as the mean of the ratios of the 20-year bin averages of the seasalt content to the total concentrations of sodium. Total sodium is used to represent seasalt in this study due to its high seasalt fraction.
TAC analysis
TAC samples were prepared using 10-cm-long sections from the second CFA cut of the SIR ice core48. At least 2 mm of the outer surfaces of the sample were removed to create plane surfaces using a sledge microtome. Subsequently, the dimensions of the elongated cube shaped samples were carefully measured using a caliper. After weighing, the approximately 60-g samples were sealed inside glass flasks and measured using a discrete wet-extraction method developed at BAS. This method is an improved volumetric vacuum-extraction technique inspired by previously developed TAC analytical methods55,56. After evacuation of the ambient air the samples were melted by two 200 W infra-red lamps. As the ice was melting, the released air and generated water vapour were allowed to expand into a previously evacuated 30-litre expansion chamber acting as an infinite gas reservoir. The stream of gas was dried using cold traps at −90 °C, removing the water vapour and only allowing the extracted air to expand into the chamber. A high-precision pressure gauge attached to the chamber and a calibrated temperature probe inside the expansion chamber allow for the calculation of TAC according to Martinerie et al. (1992)26.
The TAC data presented here were derived from 326 to 416 m below the surface. The uncertainty associated with the TAC measurement is 0.4%. The raw TAC data are typically corrected for the air released from bubbles that have been cut open during sample preparation, which is commonly known as the cut-bubble effect57. This correction requires knowledge about the precise geometrical shape of the bubbles, which is difficult to estimate and changes with depth, in particular for the topmost 100 m of the ice sheet58. The depth section investigated here lies well below 300 m depth, and the cut-bubble correction can be assumed to be constant, given that the surface to volume ratio of the prepared ice samples is kept constant. We refrain from applying this correction as it does not impact our estimation of the relative change in elevation.
The ST22 age scale
The Skytrain ice core age scale (ST22) has been developed using interpolation of annual layer counting of the top 184 m (last 2 ka) of the ice core. The age scale was refined using volcanic tie points identified using sulfate isotopes and a 1965 tritium peak59. The rest of the ice core from 184 m to 651 m was dated using the Paleochrono model60 and CH4, δ18Oair, 10Be and ice chemistry absolute tie points61. We used the version of the age scale synchronized to the WD2014 ages. Years BP is defined as years before 1950. The age uncertainty between 9 and 7 kyr BP is less than a century.
Some of the processes that affect TAC (for example, orbital insolation influence on firn structure) occur at the top of the ice sheet28. The effect of these processes on TAC therefore depends on the age of the ice rather than the gas age. Other processes are imprinted only at close-off27 and therefore appear at depths corresponding to the gas age of the event. The effect of elevation change (that is, change of barometric pressure) on TAC is assumed to be instantaneous. In this study, we therefore present the TAC data on the gas age scale while acknowledging that some of the dynamic features may correspond to the ice age. For clarity, the TAC data on the depth scale are shown in Supplementary Fig. 4.
Estimating the timing of the early Holocene transitions
The timing of the changes in δ18O and Na was determined using Rampfit62, which provides an estimate of the start and end of a linear ramp, with corresponding uncertainties in age and y value. The change in isotopes was estimated using both continuous and discrete isotope data, all averaged to 10-cm intervals. The isotope increase corresponds rather well to a linear ramp, and was robust against the use of different change windows and other parameters. The rather small uncertainties on the timing of the start and end of the isotope ramp arise from the assumption that the increase is a simple ramp between two stable levels. A larger uncertainty for the start of the ramp would be found if the ramp was allowed to start in the dip that is centred about one century before the best fit ramp in Fig. 2.
The Na change was estimated using 20-cm averages (reflecting the need for greater smoothing of the relatively noisier dataset). It occurs in two steps and is less suited to a ramp. We report the changes across the initial increase (which is akin to a ramp), while accepting that the change does not become fully locked in until later than the ages we provide.
Estimating the change in elevation based on water isotopes
δ18O is expected to fall with elevation, in parallel with the fall in temperature characterized by a lapse rate. A few studies have attempted to determine the isotope–elevation slope (which we here express as a positive number when δ18O falls with increasing elevation).
Using an Antarctic continent-wide compilation of data25, spatial slopes ranging between 0.7‰ and 0.91‰ per 100 m were derived19. Using an isotope-enabled model19, the spatial slope for a region surrounding Fletcher Promontory (which includes SIR) was determined to be a little higher than the continent-wide range at 0.95‰ per 100 m. The gradient for the change in elevation between various simulations of the LGM and the present day was 0.74 ± 0.18‰ per 100 m in the same region. Using a different model and idealized changes in elevation around the Antarctic24, a similar range of values was found at high elevation. Higher values of the slope at low elevation might be an artefact of the experimental protocol, where low-elevation sites experienced small changes in altitude but were subject to influences from much larger elevation changes inland.
Taking into account the observations and the modelled slopes derived in the region around SIR19, we propose that a slope of 0.8 ± 0.2‰ per 100 m encompasses most of the reliable evidence, and is suitable for assessing possible elevation changes implied by our isotopic data. We express elevations based on the isotope data using the central value of 0.8‰ per 100 m, and with ranges based on the uncertainty of 0.2‰ per 100 m.
Calculating the change in elevation based on TAC
To calculate a TAC-based elevation history, we employed a Monte Carlo (MC) simulation (n = 5,000) that provides an estimate for the combined uncertainty of the relative elevation drop based on the TAC analytical error (0.4%), a range of isotope-to-temperature relationships (0.8 ± 0.2‰ per degree Celsius) and a range of pore volume at bubble closure (Vc)-to-temperature relationships (0.45 ± 0.30 ml kg−1 K−1)26,63.
Atmospheric pressure at the time of bubble closure (Pc in mbar) is reconstructed from TAC, the temperature at bubble closure, and the volume at bubble closure (equation (2))
where Vc is the assumed volume per ice mass at bubble closure (ml kg−1), Tc is the temperature at bubble closure (K) and PS and Ts normalize the data to standard temperature and pressure (1,013.25 mbar and 273.15 K, respectively). The unit of TAC is ml kg−1. The resultant pressure at closure (Pc) histories are transformed into elevation using a generalized pressure–elevation equation derived for Antarctica63,64 (equation (3))
The modern Vc and temperature are fixed at 127 ml kg−1 and −26 °C (247.15 K), respectively. Thus, the changes in elevation and the associated uncertainty are all relative to modern values and the uncertainty increases as the data depart from the modern values. We note that to first order the change in elevation is proportional to ln (Pc1/Pc2), where 1 and 2 denote times before and after the change in elevation. This means that changes in any of the constants in equation (2), or a constant scaling of TAC values due to the cut bubble correction, do not significantly alter the change in elevation.
The temperature at the time when the bubbles close off controls the TAC following the ideal gas law. The temperature of the air at the moment of bubble close-off is set by the temperature of the surrounding ice, with a given amount of air taking up larger volumes at warmer temperatures. A rapid warming thus drives a decrease in TAC. All else being equal, this would lead to an inferred drop in barometric pressure and therefore an increase in surface elevation. However, because it takes several hundred years for the base of the firn to equilibrate with the surface temperature, the temperature at bubble closure is a smoothed and lagged response to the surface temperature forcing.
We modelled the temperature at bubble closure using the Community Firn Model65 forced by a surface temperature history from the high-resolution isotope data (interpolated to 1 year) and constant accumulation. Thermal conductivity is based on Calonne et al. (2019)66, and the densification is based on a dynamic version of the Herron–Langway model. The surface temperature is derived by scaling the isotope variability to a single sensitivity of 1.00‰ K−1 and pinned to the modern using an observed temperature of −26 °C. This single, smoothed temperature history at bubble closure is varied in MC simulations to mimic a greater range of isotopic-to-temperature calibrations between 0.6‰ and 1.0‰ K−1.
Additionally, the relationship between volume per mass unit of ice (Vc) and temperature at bubble closure is varied. Modern observations from Antarctica and Greenland over a wide range of temperatures and accumulation rates suggest that Vc increases with increasing temperature. The exact slope of the relationship is not well known and most probably varies depending on the overall climatology of the site. Overall, slopes can range from between 0.450 ml kg−1 K−1 for ‘warm’ sites (~−20 °C and −35 °C), which applies to SIR during the Holocene, to 1.030 ml kg−1 K−1 for cold sites if Vostok data are excluded26. Various compilations exist for a broader range of climate conditions with slopes of 0.760 ml kg−1 K−1 (ref. 26) and 0.695 ml kg−1 K−1 (ref. 67). It is currently not known whether this relationship holds or even applies back in time. We choose to set the mean to the ‘warm’ site calibration (0.45 ml kg−1 K−1) but include a range of uncertainty (±0.30 ml kg−1 K−1) that encompasses all known sites and even the possibility that Vc does not change significantly with temperature.
To calculate the relative elevation drop we first binned the predicted elevation histories into pre- and post-rise periods from 9.5 to 8.5 and 6.6 to 5.0 kyr BP, respectively. For each bin, the mean and standard deviation are calculated for all scenarios in terms of absolute elevation (Supplementary Table 1). This describes the uncertainty from both the sample-to-sample variability within a bin and the uncertainty imparted from the random and systematic errors introduced in MC simulation.
We then take the difference between the pre- and post-rise means within a given scenario to calculate a relative change in elevation. The range in the relative difference assumes we have adequately sampled the mean elevation before and after the increase and thus only encompass the errors in the MC simulation.
Estimating distances from the ice edge using sodium
Minikin et al. (1994)40 presented data showing the way that Na concentration falls with distance from the ice shelf edge on the Ronne Ice Shelf. Using their data, we plotted \(\ln [{\mathrm{Na}}]\) versus distance from the ice edge (Fig. 3). This gives a very strong correlation with R2 = 0.91. The uncertainty in the derived slope is 10%. We know very precisely the present-day Na concentration (65 ppb for 2–25 m, just over a century) and the distance from the ice edge of the drill site today (680 km). This point lies very close to the extrapolated best fit line (Fig. 3). By taking the ratio of the Na concentration before and after the increase in [Na], we can estimate the change in distance, x, from the ice edge, following equation (4),
where b is the derived slope (−0.00293), and the uncertainty is estimated from the uncertainty in the mean Na concentration before and after the increase, combined with the uncertainty of the slope. This calculation allowed us to derive the value of 270 ± 30 m for the change in distance from the ice edge in the early Holocene.
Data availability
Ice core data are available at https://doi.org/10.1594/PANGAEA.966266, https://doi.org/10.1594/PANGAEA.966226 and https://doi.org/10.1594/PANGAEA.966296. PISM model data are available at https://doi.org/10.5880/PIK.2018.008 ref. 68.
Code availability
Rampfit use was adapted from Mudelsee et al. (2000)62. The code used to calculate elevation data from TAC data is available via Zenodo (https://zenodo.org/records/10178665).
Change history
25 March 2024
A Correction to this paper has been published: https://doi.org/10.1038/s41561-024-01430-4
References
Garabato, A. C. N., McDonagh, E. L., Stevens, D. P., Heywood, K. J. & Sanders, R. J. On the export of Antarctic Bottom Water from the Weddell Sea. Deep-Sea Res. Part II: Top. Stud. Oceanogr. 49, 4715–4742 (2002).
Joughin, I. et al. Integrating satellite observations with modelling: basal shear stress of the Filcher–Ronne ice streams, Antarctica. Philos. Trans. R. Soc. A 364, 1795–1814 (2006).
Hillenbrand, C.-D. et al. Reconstruction of changes in the Weddell Sea sector of the Antarctic Ice Sheet since the Last Glacial Maximum. Quat. Sci. Rev. 100, 111–136 (2014).
Fogwill, C. et al. Drivers of abrupt Holocene shifts in West Antarctic ice stream direction determined from combined ice sheet modelling and geologic signatures. Antarctic Sci. 26, 674–686 (2014).
Schoof, C. Marine ice-sheet dynamics. Part 1. The case of rapid sliding. J. Fluid Mech. 573, 27–55 (2007).
Siegert, M., Ross, N., Corr, H., Kingslake, J. & Hindmarsh, R. Late Holocene ice-flow reconfiguration in the Weddell Sea sector of West Antarctica. Quat. Sci. Rev. 78, 98–107 (2013).
Fürst, J. J. et al. The safety band of Antarctic ice shelves. Nat. Clim. Change 6, 479–482 (2016).
Gudmundsson, G. H., Paolo, F. S., Adusumilli, S. & Fricker, H. A. Instantaneous Antarctic ice sheet mass loss driven by thinning ice shelves. Geophys. Res. Lett. 46, 13903–13909 (2019).
Johnson, J. S., Nichols, K. A., Goehring, B. M., Balco, G. & Schaefer, J. M. Abrupt mid-Holocene ice loss in the western Weddell Sea Embayment of Antarctica. Earth Planet. Sci. Lett. 518, 127–135 (2019).
Albrecht, T., Winkelmann, R. & Levermann, A. Glacial-cycle simulations of the Antarctic Ice Sheet with the Parallel Ice Sheet Model (PISM)—Part 2: Parameter ensemble analysis. Cryosphere 14, 633–656 (2020).
Bradley, S. L., Hindmarsh, R. C., Whitehouse, P. L., Bentley, M. J. & King, M. A. Low post-glacial rebound rates in the Weddell Sea due to Late Holocene ice-sheet readvance. Earth Planet. Sci. Lett. 413, 79–89 (2015).
Kingslake, J. et al. Extensive retreat and re-advance of the West Antarctic Ice Sheet during the Holocene. Nature 558, 430–434 (2018).
Wolstencroft, M. et al. Uplift rates from a new high-density GPS network in Palmer Land indicate significant late Holocene ice loss in the southwestern Weddell Sea. Geophys. J. Int. 203, 737–754 (2015).
Bentley, M. J. et al. A community-based geological reconstruction of Antarctic Ice Sheet deglaciation since the Last Glacial Maximum. Quat. Sci. Rev. 100, 1–9 (2014).
Hein, A. S. et al. Mid-Holocene pulse of thinning in the Weddell Sea sector of the West Antarctic Ice Sheet. Nat. Commun. 7, 1–8 (2016).
Siegert, M. J. et al. Major ice sheet change in the Weddell Sea Sector of West Antarctica over the last 5,000 years. Rev. Geophys. 57, 1197–1223 (2019).
Matsuoka, K. et al. Antarctic ice rises and rumples: Their properties and significance for ice-sheet dynamics and evolution. Earth Sci. Rev. 150, 724–745 (2015).
Mulvaney, R. et al. Ice drilling on Skytrain Ice Rise and Sherman Island, Antarctica. Ann. Glaciol. 62, 311–323 (2021).
Werner, M., Jouzel, J., Masson-Delmotte, V. & Lohmann, G. Reconciling glacial Antarctic water stable isotopes with ice sheet topography and the isotopic paleothermometer. Nat. Commun. 9, 1–10 (2018).
Jones, T. R. et al. Seasonal temperatures in West Antarctica during the Holocene. Nature 613, 292–297 (2023).
Kaufman, D. et al. Holocene global mean surface temperature, a multi-method reconstruction approach. Sci. Data 7, 201 (2020).
Marcott, S. A., Shakun, J. D., Clark, P. U. & Mix, A. C. A reconstruction of regional and global temperature for the past 11,300 years. Science 339, 1198–1201 (2013).
Buizert, C. et al. Antarctic surface temperature and elevation during the Last Glacial Maximum. Science 372, 1097–1101 (2021).
Goursaud, S. et al. Antarctic Ice Sheet elevation impacts on water isotope records during the last interglacial. Geophys. Res. Lett. 48, e2020GL091412 (2021).
Masson-Delmotte, V. et al. A review of Antarctic surface snow isotopic composition: observations, atmospheric circulation, and isotopic modeling. J. Clim. 21, 3359–3387 (2008).
Martinerie, P., Raynaud, D., Etheridge, D. M., Barnola, J.-M. & Mazaudier, D. Physical and climatic parameters which influence the air content in polar ice. Earth Planet. Sci. Lett. 112, 1–13 (1992).
Eicher, O. et al. Climatic and insolation control on the high-resolution total air content in the NGRIP ice core. Clim. Past. 12, 1979–1993 (2016).
Raynaud, D. et al. The local insolation signature of air content in Antarctic ice. A new step toward an absolute dating of ice records. Earth Planet. Sci. Lett. 261, 337–349 (2007).
De Leeuw, G. et al. Production flux of sea spray aerosol. Rev. Geophys. 49 https://doi.org/10.1029/2010RG000349 (2011).
Frey, M. M. et al. First direct observation of sea salt aerosol production from blowing snow above sea ice. Atmos. Chem. Phys. 20, 2549–2578 (2020).
Guelle, W., Schulz, M., Balkanski, Y. & Dentener, F. Influence of the source formulation on modeling the atmospheric global distribution of sea salt aerosol. J. Geophys. Res. Atmos. 106, 27509–27524 (2001).
Abram, N. J., Wolff, E. W. & Curran, M. A. J. A review of sea ice proxy information from polar ice cores. Quat. Sci. Rev. 79, 168–183 (2013).
Levine, J. G., Yang, X., Jones, A. E. & Wolff, E. W. Sea salt as an ice core proxy for past sea ice extent: A process-based model study. J. Geophys. Res. Atmos. 119, 5737–5756 (2014).
Pasteris, D. R. et al. Seasonally resolved ice core records from West Antarctica indicate a sea ice source of sea-salt aerosol and a biomass burning source of ammonium. J. Geophys. Res. Atmos. 119, 9168–9182 (2014).
Winski, D. A. et al. Seasonally resolved Holocene sea ice variability inferred from South Pole ice core chemistry. Geophys. Res. Lett. 48, e2020GL091602 (2021).
Wolff, E. W., Rankin, A. M. & Röthlisberger, R. An ice core indicator of Antarctic sea ice production? Geophys. Res. Lett. 30 https://doi.org/10.1029/2003GL018454 (2003).
Markle, B. R., Steig, E. J., Roe, G. H., Winckler, G. & McConnell, J. R. Concomitant variability in high-latitude aerosols, water isotopes and the hydrologic cycle. Nat. Geosci. 11, 853–859 (2018).
Wagenhach, D. et al. Reconnaissance of chemical and isotopic firn properties on top of Berkner Island, Antarctica. Ann. Glaciol. 20, 307–312 (1994).
Bertler, N. et al. Snow chemistry across Antarctica. Ann. Glaciol. 41, 167–179 (2005).
Minikin, A., Wagenbach, D., Graf, W. & Kipfstuhl, J. Spatial and seasonal variations of the snow chemistry at the central Filchner-Ronne Ice Shelf, Antarctica. Ann. Glaciol. 20, 283–290 (1994).
Winter, K. et al. Airborne radar evidence for tributary flow switching in Institute Ice Stream, West Antarctica: implications for ice sheet configuration and dynamics. J. Geophys. Res. Earth Surf. 120, 1611–1625 (2015).
Balco, G. et al. Cosmogenic-nuclide exposure ages from the Pensacola Mountains adjacent to the Foundation Ice Stream, Antarctica. Am. J. Sci. 316, 542–577 (2016).
Bentley, M. J. et al. Deglacial history of the Pensacola Mountains, Antarctica from glacial geomorphology and cosmogenic nuclide surface exposure dating. Quat. Sci. Rev. 158, 58–76 (2017).
Nichols, K. A. et al. New Last Glacial Maximum ice thickness constraints for the Weddell Sea Embayment, Antarctica. Cryosphere 13, 2935–2951 (2019).
Bentley, M. J., Fogwill, C. J., Kubik, P. W. & Sugden, D. E. Geomorphological evidence and cosmogenic 10Be/26Al exposure ages for the Last Glacial Maximum and deglaciation of the Antarctic Peninsula Ice Sheet. Geol. Soc. Am. Bull. 118, 1149–1159 (2006).
Jones, R. et al. Rapid Holocene thinning of an East Antarctic outlet glacier driven by marine ice sheet instability. Nat. Commun. 6, 8910 (2015).
Stutz, J. et al. Mid-Holocene thinning of David Glacier, Antarctica: chronology and controls. Cryosphere 15, 5447–5471 (2021).
Grieman, M. M. et al. Continuous flow analysis methods for sodium, magnesium and calcium detection in the Skytrain ice core. J. Glaciol. 68, 90–100 (2022).
Matsuoka, K. et al. Quantarctica, an integrated mapping environment for Antarctica, the Southern Ocean, and sub-Antarctic Islands. Environ. Model. Softw. 140, 105015 (2021).
Mulvaney, R., Alemany, O. & Possenti, P. The Berkner Island (Antarctica) ice-core drilling project. Ann. Glaciol. 47, 115–124 (2007).
Fischer, H. et al. Reconstruction of millennial changes in dust emission, transport and regional sea ice coverage using the deep EPICA ice cores from the Atlantic and Indian Ocean sector of Antarctica. Earth Planet. Sci. Lett. 260, 340–354 (2007).
Maselli, O. J. et al. Sea ice and pollution-modulated changes in Greenland ice core methanesulfonate and bromine. Clim. Past 13, 39–59 (2017).
Röthlisberger, R. et al. Dust and sea salt variability in central East Antarctica (Dome C) over the last 45 kyrs and its implications for southern high-latitude climate. Geophys. Res. Lett. 29, 1963 (2002).
Bowen, H. J. M. Environmental Chemistry of the Elements (Academic Press, 1979).
Lipenkov, V., Candaudap, F., Ravoire, J., Dulac, E. & Raynaud, D. A new device for the measurement of air content in polar ice. J. Glaciol. 41, 423–429 (1995).
Schmitt, J., Seth, B., Bock, M. & Fischer, H. Online technique for isotope and mixing ratios of CH4, N2O, Xe and mixing ratios of organic trace gases on a single ice core sample. Atmos. Meas. Techn. 7, 2645–2665 (2014).
Martinerie, P., Lipenkov, V. & Raynaud, D. Correction of air-content measurements in polar ice for the effect of cut bubbles at the surface of the sample. J. Glaciol. 36, 299–303 (1990).
Mitchell, L. et al. Observing and modeling the influence of layering on bubble trapping in polar firn. J. Geophys. Res. Atmos. 6, 2558–2574 (2015).
Hoffmann, H. M. et al. The ST22 chronology for the Skytrain Ice Rise ice core—Part 1: A stratigraphic chronology of the last 2000 years. Clim. Past 18, 1831–1847 (2022).
Parrenin, F. et al. IceChrono1: a probabilistic model to compute a common and optimal chronology for several ice cores. Geosci. Model Dev. 8, 1473–1492 (2015).
Mulvaney, R. et al. The ST22 chronology for the Skytrain Ice Rise ice core—Part 2: An age model to the last interglacial and disturbed deep stratigraphy. Clim. Past 19, 851–864 (2023).
Mudelsee, M. Ramp function regression: a tool for quantifying climate transitions. Comput. Geosci. 26, 293–307 (2000).
Fegyveresi, J. M. Physical Properties of the West Antarctic Ice Sheet (WAIS) Divide Deep Core: Development, Evolution, and Interpretation. Ph.D. thesis, Pennsylvania State Univ. (2015).
Stone, J. O. Air pressure and cosmogenic isotope production. J. Geophys. Res. Solid Earth 105, 23753–23759 (2000).
Stevens, C. M. et al. The community firn model (CFM) v1. 0. Geosci. Model Dev. 13, 4355–4377 (2020).
Calonne, N. et al. Thermal conductivity of snow, firn, and porous ice from 3-D image-based computations. Geophys. Res. Lett. 46, 13079–13089 (2019).
Delmotte, M., Raynaud, D., Morgan, V. & Jouzel, J. Climatic and glaciological information inferred from air-content measurements of a Law Dome (East Antarctica) ice core. J. Glaciol. 45, 255–263 (1999).
Albrecht, T. PISM simulation results of the Antarctic Ice Sheet deglaciation. GFZ Data Services https://doi.org/10.5880/PIK.2018.008 (2018).
Acknowledgements
This project received funding from the European Research Council under the Horizon 2020 research and innovation programme (grant agreement no. 742224, WACSWAIN). This material reflects only the authors’ views, and the Commission is not liable for any use that may be made of the information contained therein. E.W.W. and H.M.H. have been funded through a Royal Society Professorship. The authors thank R. Tuckwell, J. Rix, E. Doyle, C. McKeever and S. Polfrey for ice core drilling support; S. Miller, E. Ludlow and V. Alcock for help with cutting and processing the ice core; J. Humby and C. Durman for help with the CFA analysis; and C. Martin and H. Pryer for valuable discussions. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.
Author information
Authors and Affiliations
Contributions
E.W.W. and R.M. planned the WACSWAIN project. R.M., E.W.W., C.N.-A. and M.M.G. took part in drilling the ice core. R.M., E.W.W., C.N.-A., A.C.F.K., I.F.R. and M.M.G. sampled (cut) the ice core for analysis. H.M.H., I.F.R., E.R.T. and M.M.G. performed the CFA laboratory analysis. M.M.G. analysed the CFA data. C.N.-A. developed the TAC method. C.N.-A., T.K.B. and A.C.F.K. performed the TAC laboratory analysis and analysed the TAC data. T.K.B. analysed the published ice sheet model output. M.M.G., E.W.W., R.H.R., T.K.B., C.N.-A. and H.M.H. interpreted the records and wrote the paper. All authors edited the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Geoscience thanks Keir Nichols, Martin Wearing and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: James Super, in collaboration with the Nature Geoscience team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Table 1 and Figs. 1–5.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grieman, M.M., Nehrbass-Ahles, C., Hoffmann, H.M. et al. Abrupt Holocene ice loss due to thinning and ungrounding in the Weddell Sea Embayment. Nat. Geosci. 17, 227–232 (2024). https://doi.org/10.1038/s41561-024-01375-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41561-024-01375-8
This article is cited by
-
Simulating the aftermath of Northern European Enclosure Dam (NEED) break and flooding of European coast
Engineering with Computers (2024)