Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Longitudinal structure of Earth’s magnetic field controlled by lower mantle heat flow

Nature Geoscience (2023)Cite this article

Subjects

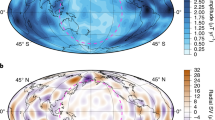
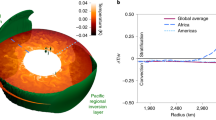
Abstract

Thermal interactions between Earth’s core and mantle provide the power that maintains the geomagnetic field. However, the effect of these interactions and, in particular, the thermochemical piles at the base of the mantle on magnetic field behaviour remains uncertain. Here we present numerical dynamo simulations with strong lateral variations in heat flow imposed at the core–mantle boundary to reproduce conditions within Earth and indicate how the mantle controls core dynamics. Comparing these simulations to recent global magnetic field models, based on observational data spanning tens of thousands of years, they successfully reproduce the morphology and secular variation of Earth’s modern field and the inferred large-scale flow structure at the top of the core. These simulations reveal that the long-term geomagnetic signatures of thermal core–mantle interactions are evident in the longitudinal structure of the geomagnetic field as equatorial patches of reverse flux, rather than the high-latitude patches suggested by less Earth-like simulations. Comparison of these simulations with the field models also suggests that the amplitude of the present-day longitudinal hemispheric imbalance in secular variation is anomalously large, indicating our present-day geomagnetic field may be unusual.

This is a preview of subscription content, access via your institution

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Time-averaged magnetic fields for our simulations.
Fig. 2: Comparison of our Ra = 2,000 and q* = 2.3 simulation with gufm1.
Fig. 3: The longitudinal variation in Pi.
Fig. 4: Time-averaged radial magnetic field at the CMB in the equatorial regions of the simulations.

Data availability

Original data underlying the figures and plain text versions of tables are available at github.com/jonmound/MD2023data.

Code availability

For access to the github repository containing the Leeds dynamo code, please contact the corresponding author.

References

  1. Landeau, M., Fournier, A., Nataf, H.-C., Cébron, D. & Schaeffer, N. Sustaining Earth’s magnetic dynamo. Nat. Rev. Earth Environ. 3, 255–269 (2022).

    Article  Google Scholar 

  2. Nakagawa, T. & Tackley, P. J. Lateral variations in CMB heat flux and deep mantle seismic velocity caused by a thermal-chemical-phase boundary layer in 3D spherical convection. Earth Planet. Sci. Lett. 271, 348–358 (2008).

    Article  Google Scholar 

  3. Stackhouse, S., Stixrude, L. & Karki, B. B. First-principles calculations of the lattice thermal conductivity of the lower mantle. Earth Planet. Sci. Lett. 427, 11–17 (2015).

    Article  Google Scholar 

  4. Olson, P., Coe, R., Driscoll, P., Glatzmaier, G. & Roberts, P. Geodynamo reversal frequency and heterogeneous core–mantle boundary heat flow. Phys. Earth Planet. Inter. 180, 66–79 (2010).

    Article  Google Scholar 

  5. Laj, C., Mazaud, A., Weeks, R., Fuller, M. & Herrrero-Bervera, E. Geomagnetic reversal paths. Nature 351, 447 (1991).

    Article  Google Scholar 

  6. Doell, R. R. & Cox, A. Pacific geomagnetic secular variation. Science 171, 248–254 (1971).

    Article  Google Scholar 

  7. Gubbins, D. in Earth’s Core: Dynamics, Structure, Rotation (eds Dehant, V. et al.) 163–179 (American Geophysical Union, 2003).

  8. Panovska, S., Constable, C. G. & Korte, M. Extending global continuous geomagnetic field reconstructions on timescales beyond human civilization. Geochem. Geophys. Geosyst. 19, 4757–4772 (2018).

    Article  Google Scholar 

  9. Jackson, A., Jonkers, A. R. T. & Walker, M. R. Four centuries of geomagnetic secular variation from historical records. Philos. Trans. R. Soc. A 358, 957–990 (2000).

    Article  Google Scholar 

  10. Panovska, S., Korte, M. & Constable, C. G. One hundred thousand years of geomagnetic field evolution. Rev. Geophys. 57, 1289–1337 (2019).

    Article  Google Scholar 

  11. Finlay, C. C. et al. The CHAOS-7 geomagnetic field model and observed changes in the South Atlantic Anomaly. Earth Planets Space 72, 156 (2020).

    Article  Google Scholar 

  12. Panovska, S. & Constable, C. G. An activity index for geomagnetic paleosecular variation, excursions, and reversals. Geochem. Geophys. Geosyst. 18, 1366–1375 (2017).

    Article  Google Scholar 

  13. Korte, M. & Constable, C. Improving geomagnetic field reconstructions for 0–3 ka. Phys. Earth Planet. Inter. 188, 247–259 (2011).

    Article  Google Scholar 

  14. Korte, M., Constable, C., Donadini, F. & Holme, R. Reconstructing the Holocene geomagnetic field. Earth Planet. Sci. Lett. 312, 497–505 (2011).

    Article  Google Scholar 

  15. Nilsson, A., Holme, R., Korte, M., Suttie, N. & Hill, M. Reconstructing Holocene geomagnetic field variation: new methods, models and implications. Geophys. J. Int. 198, 229–248 (2014).

    Article  Google Scholar 

  16. Mound, J., Davies, C. & Silva, L. Inner core translation and the hemispheric balance of the geomagnetic field. Earth Planet. Sci. Lett. 424, 148–157 (2015).

    Article  Google Scholar 

  17. Holme, R. Large-Scale Flow in the Core: Treatise on Geophysics 2nd edn (Elsevier, 2015).

  18. Jackson, A., Bloxham, J. & Gubbins, D. in Dynamics of Earth’s Deep Interior and Earth Rotation (eds J.-L. Le Mouël, D. E. Smylie & T. Herring) 97–107 (IUGG and AGU, 1993).

  19. Barrois, O., Hammer, M. D., Finlay, C. C., Martin, Y. & Gillet, N. Assimilation of ground and satellite magnetic measurements: inference of core surface magnetic and velocity field changes. Geophys. J. Int. 215, 695–712 (2018).

    Article  Google Scholar 

  20. Whaler, K. A., Hammer, M. D., Finlay, C. C. & Olsen, N. Core surface flow changes associated with the 2017 Pacific geomagnetic jerk. Geophys. Res. Lett. 49, e2022GL098616 (2022).

    Article  Google Scholar 

  21. Pais, M. A. & Jault, D. Quasi-geostrophic flows responsible for the secular variation of the Earth’s magnetic field. Geophys. J. Int. 173, 421–443 (2008).

    Article  Google Scholar 

  22. Gillet, N., Jault, D. & Finlay, C. C. Planetary gyre, time-dependent eddies, torsional waves and equatorial jets at the Earth’s core surface. J. Geophys. Res. B: Solid Earth 120, 3991–4013 (2015).

    Article  Google Scholar 

  23. Willis, A. P., Sreenivasan, B. & Gubbins, D. Thermal core–mantle interaction: exploring regimes for ‘locked’ dynamo action. Phys. Earth Planet. Inter. 165, 83–92 (2007).

    Article  Google Scholar 

  24. Christensen, U. R., Aubert, J. & Hulot, G. Conditions for Earth-like geodynamo models. Earth Planet. Sci. Lett. 296, 487–496 (2010).

    Article  Google Scholar 

  25. Davies, C. J. & Constable, C. G. Insights from geodynamo simulations into long-term geomagnetic field behaviour. Earth Planet. Sci. Lett. 404, 238–249 (2014).

    Article  Google Scholar 

  26. Aubert, J., Finlay, C. C. & Fournier, A. Bottom-up control of geomagnetic secular variation by the Earth’s inner core. Nature 502, 219–223 (2013).

    Article  Google Scholar 

  27. Davies, C. J., Stegman, D. R. & Dumberry, M. The strength of gravitational core–mantle coupling. Geophys. Res. Lett. 41, 3786–3792 (2014).

    Article  Google Scholar 

  28. Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. Thermal and electrical conductivity of solid iron and iron–silicon mixtures at Earth’s core conditions. Earth Planet. Sci. Lett. 393, 159–164 (2014).

    Article  Google Scholar 

  29. Labrosse, S. Thermal and compositional stratification of the inner core. C.R. Geosci. 346, 119–129 (2014).

    Article  Google Scholar 

  30. Lythgoe, K. H., Rudge, J. F., Neufeld, J. A. & Deuss, A. The feasibility of thermal and compositional convection in Earth’s inner core. Geophys. J. Int. 201, 764–782 (2015).

    Article  Google Scholar 

  31. Deguen, R., Alboussiére, T. & Labrosse, S. Double-diffusive translation of Earth’s inner core. Geophys. J. Int. 214, 88–107 (2018).

    Google Scholar 

  32. Gubbins, D. & Kelly, P. Persistent patterns in the geomagnetic field over the past 2.5 Myr. Nature 365, 829–832 (1993).

    Article  Google Scholar 

  33. Gubbins, D., Willis, A. P. & Sreenivasan, B. Correlation of Earth’s magnetic field with lower mantle thermal and seismic structure. Phys. Earth Planet. Inter. 162, 256–260 (2007).

    Article  Google Scholar 

  34. Olson, P., Landeau, M. & Reynolds, E. Dynamo tests for stratification below the core–mantle boundary. Phys. Earth Planet. Int. 271, 1–18 (2017).

    Article  Google Scholar 

  35. Meduri, D. G. et al. Numerical dynamo simulations reproduce paleomagnetic field behavior. Geophys. Res. Lett. 48, e2020GL090544 (2021).

    Article  Google Scholar 

  36. Aubert, J., Gastine, T. & Fournier, A. Spherical convective dynamos in the rapidly rotating asymptotic regime. J. Fluid Mech. 813, 558–593 (2017).

    Article  Google Scholar 

  37. Aubert, J. Approaching Earth’s core conditions in high-resolution geodynamo simulations. Geophys. J. Inter. 219, S137–S151 (2019).

    Article  Google Scholar 

  38. Davies, C. J. & Mound, J. E. Mantle-induced temperature anomalies do not reach the inner core boundary. Geophys. J. Inter. 219, S21–S32 (2019).

    Article  Google Scholar 

  39. Mound, J. E. & Davies, C. J. Scaling laws for regional stratification at the top of Earth’s core. Geophys. Res. Lett. 47, e2020GL087715 (2020).

    Article  Google Scholar 

  40. Olson, P. & Christensen, U. R. The time-averaged magnetic field in numerical dynamos with non-uniform boundary heat flow. Geophys. J. Inter. 151, 809–823 (2002).

    Article  Google Scholar 

  41. Sahoo, S. & Sreenivasan, B. Response of Earth’s magnetic field to large lower mantle heterogeneity. Earth Planet. Sci. Lett. 549, 116507 (2020).

    Article  Google Scholar 

  42. Finlay, C. C., Jackson, A., Gillet, N. & Olsen, N. Core surface magnetic field evolution 2000–2010. Geophys. J. Inter. 189, 761–781 (2012).

    Article  Google Scholar 

  43. Dumberry, M. & More, C. Weak magnetic field changes over the Pacific due to high conductance in lowermost mantle. Nat. Geosci. 13, 516–520 (2020).

    Article  Google Scholar 

  44. Masters, G., Johnson, S., Laske, G. & Bolton, H. A shear-velocity model of the mantle. Phil. Trans. R. Soc. A 354, 1385–1411 (1996).

    Article  Google Scholar 

  45. Holme, R., Olsen, N. & Bairstow, F. L. Mapping geomagnetic secular variation at the core–mantle boundary. Geophys. J. Inter. 186, 521–528 (2011).

    Article  Google Scholar 

  46. Mound, J. E. & Davies, C. J. Heat transfer in rapidly rotating convection with heterogeneous thermal boundary conditions. J. Fluid Mech. 828, 601–629 (2017).

    Article  Google Scholar 

  47. Mound, J., Davies, C., Rost, S. & Aurnou, J. Regional stratification at the top of Earth’s core due to core–mantle boundary heat flux variations. Nat. Geosci. 12, 575–580 (2019).

    Article  Google Scholar 

  48. Long, R. S., Mound, J. E., Davies, C. J. & Tobias, S. M. Scaling behaviour in spherical shell rotating convection with fixed-flux thermal boundary conditions. J. Fluid Mech. 889, A7 (2020).

    Article  Google Scholar 

  49. Schaeffer, N., Jault, D., Nataf, H. C. & Fournier, A. Turbulent geodynamo simulations: a leap towards Earth’s core. Geophys. J. Inter. 211, 1–29 (2017).

    Article  Google Scholar 

  50. McNamara, A. K. A review of large low shear velocity provinces and ultra low velocity zones. Tectonophysics 760, 199–220 (2019).

    Article  Google Scholar 

  51. Olson, P., Deguen, R., Rudolph, M. L. & Zhong, S. Core evolution driven by mantle global circulation. Phys. Earth Planet. Inter. 243, 44–55 (2015).

    Article  Google Scholar 

  52. Dziewonski, A. M. & Anderson, D. L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356 (1981).

    Article  Google Scholar 

  53. Ichikawa, H., Tsuchiya, T. & Tange, Y. The P–V–T equation of state and thermodynamic properties of liquid iron. J. Geophys. Res. 119, 240–252 (2014).

    Article  Google Scholar 

  54. Davies, C., Pozzo, M., Gubbins, D. & Alfè, D. Constraints from material properties on the dynamics and evolution of Earth’s core. Nat. Geosci. 8, 678–685 (2015).

    Article  Google Scholar 

  55. Konôpková, Z., McWilliams, R. S., Gómez-Pérez, N. & Goncharov, A. F. Direct measurement of thermal conductivity in solid iron at planetary core conditions. Nature 534, 99–101 (2016).

    Article  Google Scholar 

  56. Hirose, K., Wood, B. & Voçadlo, L. Light elements in the Earth’s core. Nat. Rev. Earth Environ. 2, 645–658 (2021).

    Article  Google Scholar 

  57. Tassin, T., Gastine, T. & Fournier, A. Geomagnetic semblance and dipolar–multipolar transition in top-heavy double-diffusive geodynamo models. Geophys. J. Inter. 226, 1897–1919 (2021).

    Article  Google Scholar 

  58. Aurnou, J. M. et al. Rotating convective turbulence in Earth and planetary cores. Phys. Earth Planet. Inter. 246, 52–71 (2015).

    Article  Google Scholar 

  59. Orszag, S. A. Numerical simulation of incompressible flows within simple boundaries. I. Galerkin (spectral) representations. Stud. Appl. Math. 50, 293–327 (1971).

    Article  Google Scholar 

  60. Schwaiger, T., Gastine, T. & Aubert, J. Force balance in numerical geodynamo simulations: a systematic study. Geophys. J. Inter. 219, S101–S114 (2019).

    Article  Google Scholar 

  61. Hunter, J. D. Matplotlib: a 2D graphics environment. Comput. Sci. Eng. 9, 90–95 (2007).

    Article  Google Scholar 

  62. Cartopy: A Cartographic Python Library with a Matplotlib Interface (Met Office, 2015); http://scitools.org.uk/cartopy

Download references

Acknowledgements

We thank C. Constable for useful discussion that improved this work. C.J.D. acknowledges funding via a Natural Environment Research Council Pushing the Frontiers award, reference NE/V010867/1. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript. Figures were produced using Matplotlib61 and Cartopy62. This work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk) and ARC2, part of the High Performance Computing facilities at the University of Leeds, UK.

Author information

Authors and Affiliations

  1. School of Earth and Environment, University of Leeds, Leeds, UK

    Jonathan E. Mound & Christopher J. Davies

Authors
  1. Jonathan E. Mound
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Christopher J. Davies
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.E.M. and C.J.D. both conceived of the study, carried out and analysed the simulations and co-wrote the paper.

Corresponding author

Correspondence to Jonathan E. Mound.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Geoscience thanks Nathanaël Schaeffer, Andreas Nilsson and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Louise Hawkins, in collaboration with the Nature Geoscience team.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Time-averaged magnetic fields.

Time-averaged magnetic fields. Maps are for GGF100k (a) and our simulations with Ra = 6000 and q* = 2.3, 5.0 (b,c). The radial component of the magnetic field on the CMB truncated at spherical harmonic degree and order 4. Note that the simulations use a non-dimensional scale.

Extended Data Fig. 2 Evolution of the contributions to magnetic field and secular variation semblance over our simulations.

Evolution of the contributions to magnetic field and secular variation semblance over our simulations. The χ2 contribution from the O/E, Z/NZ, AD/NAD, FCF, and Hsv measures are given by the orange, green, red, purple, and brown filled areas, respectively. The black solid line highlights the sum of the four compliance criteria for the magnetic field geometry and the grey horizontal lines indicate the values below which this total compliance is considered excellent, good, or marginal in comparison with Earth as derived from gufm1. Values to the right of each panel indicate the percentage of 400-year windows that fall in each compliance band. Simulations have Ra = 2000 (panels a,b,c) or Ra = 6000 (panels d,e,f) and q* = 0.0 (a,d), q* = 2.3 (b,e), or q* = 5.0 (c,f).

Extended Data Fig. 3 Time-averaged radial magnetic field at the core–mantle boundary in the equatorial regions of the simulations.

Time-averaged radial magnetic field at the core–mantle boundary in the equatorial regions of the simulations. Runs are characterised by Ra = 6000 and q* = 2.3, 5 (a,b). Both plots use the same colour scale for the (non-dimensional) magnetic field strength and are truncated at spherical harmonic degree and order 8.

Extended Data Fig. 4 Time-averaged values of the paleosecular variation index from our simulations.

Time-averaged values of the paleosecular variation index from our simulations. Runs are characterised by Ra = 2000 and q* = 0, 2.3, 5 (a,c,e); Ra = 6000 and q* = 2.3, 5 (d,f). The final map is GGF100k (b). All plots use the same colour scale.

Extended Data Table 1 Dynamo Parameters that Vary Between Runs
Full size table
Extended Data Table 2 Geomagnetic Field Measures
Full size table

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Mound, J.E., Davies, C.J. Longitudinal structure of Earth’s magnetic field controlled by lower mantle heat flow. Nat. Geosci. (2023). https://doi.org/10.1038/s41561-023-01148-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1038/s41561-023-01148-9

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing