Abstract
Angular momentum is fundamental to the structure and variability of the atmosphere and therefore has an important influence on regional weather and climate. Total atmospheric angular momentum is also directly related to the rotation rate of the Earth and, hence, the length of day. However, the long-range predictability of fluctuations in the length of the day and atmospheric angular momentum is unknown. Here we show that fluctuations in atmospheric angular momentum and the length of day are predictable out to more than a year ahead and that this provides an atmospheric source of long-range predictability for surface climate. Using ensemble forecasts from a dynamical climate model, we demonstrate long-range predictability of signals in the atmospheric angular momentum field that propagate slowly and coherently polewards due to wave–mean flow interaction within the atmosphere. These predictable signals are also shown to precede changes in extratropical climate via the North Atlantic Oscillation and the extratropical jet stream. These results extend the lead time for length-of-day predictions, provide a source of long-range predictability from within the atmosphere and provide a link between geodesy and climate prediction.
Similar content being viewed by others
Main
Earth and its atmosphere are largely isolated in space and therefore conserve total angular momentum to a close approximation. Notwithstanding effects on long timescales due to changes in the angular momentum of Earth’s fluid core and oceans1, many of the fluctuations seen in the rotation rate of Earth and hence the length of day can be explained by exchange of axial angular momentum between Earth and the atmosphere2,3,4. Prominent fluctuations in the length of day have been attributed to weather phenomena on monthly timescales such as the Madden Julian Oscillation5,6, and skilful forecasts of the length of day have been developed using weather forecast information. Length-of-day forecasts are used for accurate global positioning using satellites, for pointing of astronomical instruments and for deep space navigation. There have also been attempts at seasonal predictions of length of day using statistical-empirical forecasts as these are useful for re-acquisition of satellite signals after long instrumental off-line periods7 and have even been connected to fluctuations in geohazards such as earthquakes8. However, although studies with idealized models have shown long-lived atmospheric angular momentum (AAM) anomalies9,10,11, whether they are predictable at long lead times and whether they can lead to long-range prediction of weather and climate are unknown. Here we demonstrate long-range predictability of AAM and the length of day, and we show how AAM fluctuations that migrate slowly polewards are not only predictable on interannual timescales but also precede extratropical climate fluctuations.
Long-range predictability of length of day
Fluctuations in the length of day derived from radio telescope measurements of distant astronomical sources (for the geodetic observation of length-of-day variations, see Methods) are shown in Fig. 1. It is these anomalies in the length of day that we first aim to predict. We use the Met Office Hadley Centre Global Environmental Model of the atmosphere and ocean, initialized with observational analyses, to predict atmospheric angular momentum (for the calculation of AAM, see Methods). This model knows nothing of the fluctuations in Earth’s rotation rate, but it has been demonstrated in previous studies to accurately predict the main sources of interannual climate variability in the tropics and extratropics months to years ahead12,13,14,15. Ensembles of ten retrospective forecasts started each year in November show fluctuations of ~1025 kg m2 s−1 in global AAM between years, which corresponds to ~0.5 × 10−3 s in the length of day and compares well with observed fluctuations (Fig. 1a). A summary of the predictability of the length of day in model forecasts is shown in Fig. 1b. To calculate the so-called perfect model predictability within our forecasts, we first calculate correlations between each ensemble member and the mean of the remaining ensemble members (Fig. 1b). This measure of the ability of the model to predict its own forecast members remains above 0.8 for the first few months of the forecast, suggesting very high potential predictability of the modelled AAM and hence the length of day within our model forecast system. As expected, this modelled predictability then decreases with lead time into the forecast. However, it reaches a minimum in the following boreal summer and autumn before rising again in winter, over a year after the start of the forecast. This is followed by a second drop in skill with residual predictability out to around two years ahead. A similar variation is found in the actual forecast skill when we use the model ensemble mean to predict the observed length of day from either radio telescope observations or observational analysis of atmospheric angular momentum. Similar peaks are again found in the first and second winters in the skill for predicting observed length-of-day variations, and skill again extends out to over a year ahead. Naturally, the scores are statistically noisier in this case as there is only one realization of the observed length of day whereas the model perfect predictability is an average of the scores over ten cases, one for each ensemble member. Nevertheless, these results demonstrate that total atmospheric angular momentum is among the most highly predictable characteristics of Earth’s atmosphere, with forecast skill scores that decline non-monotonically with lead time. This behaviour resembles the skill of predictions of the El Niño/Southern Oscillation (ENSO)14,16. Indeed, our monthly angular momentum predictions in the first few months of the forecast show a correlation of ~0.7 with the monthly Niño3.4 ENSO index, consistent with the known triggering of AAM anomalies often by ENSO17,18,19.
a, Variations in the length of day (LOD) showing the prominent interannual variability of around 0.5 × 10−3 s in observations (black) and the first year of ensemble mean model predictions starting in November each year (red). b, Correlation of predicted seasonal length-of-day anomalies in the ensemble mean with length-of-day anomalies from single model ensemble members (black), with radio telescope observations of Earth’s rotation (blue) and with atmospheric reanalysis (red). The perfect model predictability (black) is smoother than the prediction skill against observations (red, blue) due to averaging of the correlations with each ensemble member in the model case. Note the non-monotonic variation with lead time and the peaks at leads of 3 and 15 months in winter. Statistical significance at the 95% level according to a one-sided t test for positive correlations is shown by the dotted line.
Predictable migrating signals
So far, we have considered only globally integrated atmospheric angular momentum and the length of day. However, regional analyses of AAM have also been possible since early reanalyses of global atmospheric winds and density were first constructed20. A comparison between predicted and observed angular momentum anomaly structures is shown in Fig. 2 as a function of latitude and time. Observed and predicted AAM anomalies fluctuate between similar amplitude positive and negative values, originating in the subtropics and propagating polewards. Large anomalies in global AAM show a particular latitudinal structure that first peaks around 20–30° N and 20–30° S (Fig. 2) and is roughly symmetric about the Equator. We noted earlier the previous findings that the tropical origin of large AAM anomalies is often related to ENSO variability17,18,19, and these initial subtropical signatures are consistent with known ENSO-induced changes in the strength of the subtropical jets. However, unlike ENSO events, which decline over a few months in spring, predicted AAM anomalies persist throughout the following year. They can often be traced for over a year as they propagate coherently polewards out of the tropics into both hemispheres, before terminating near 50° N and 50° S in a similar manner to the propagation of observed AAM anomalies18,21. The skill of the predicted AAM as a function of lead time and latitude is shown in Fig. 2c, and positive prediction skill is found at all lead times between the latitudes where propagating AAM anomalies occur. There is also a signature of increased skill after one year, in agreement with the skill of global AAM and length-of-day predictions in Fig. 1. This confirms that predictable signals reach the mid-latitudes, persisting for more than a year after they are initiated (Fig. 2) and long after the ENSO events that trigger the initial AAM anomalies have declined.
a,b, Latitude–time plots of zonally integrated AAM anomalies are shown for a 20-year sample period from observational analysis (a) and corresponding ensemble means for the first year of each forecast from 1980 to 2000 (b). Vertical lines represent November each year, when forecasts are initialized. Units are 1024 kg m2 s−1 per 0.55° latitude band, and the mean seasonal cycle has been removed from each latitude. Observational analyses are taken from the ERA datasets35,36. c, The correlation skill of the ensemble mean predictions as a function of latitude and lead time (months) for the whole period (1960–2017) using running seasonal means and a 6° latitudinal averaging.
Atmospheric wave driving
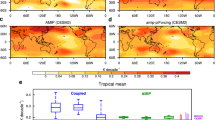
Studies using idealized atmospheric models and observations have previously identified analogous long-lived zonal wind signatures that persist and migrate polewards by internal wave forcing without any external forcing9,10,11,22,. Zonal flow variations in the extratropics of both hemispheres are also known to involve positive feedback from transient eddies10,23. Figure 3a shows the structure of the predicted angular momentum anomalies and the atmospheric wave driving of zonal winds and hence axial angular momentum. We measure the atmospheric wave driving using the Eliassen–Palm flux24. The Eliassen–Palm flux represents the net effect of atmospheric eddy momentum and heat fluxes on the zonal mean momentum budget, and it is calculated from the atmospheric state in each of our ensemble predictions. The wave-driven acceleration (Fig. 3a) is of order 0.1 m s−1 d−1 and is displaced polewards of the peak in AAM. This phase relation between the AAM anomalies and the wave driving leads to forcing on the poleward side of the AAM anomaly and hence leads to propagation of the AAM anomalies into the extratropics, confirming that the atmosphere is driving the AAM signals. Figure 3a also shows the wave driving from stationary waves alone, which is small compared with the total wave driving. This confirms that it is transient waves (with non-zero phase speeds) that provide the bulk of the forcing. The schematic (Fig. 3b–d) illustrates how the mechanism can be understood in terms of the meridional propagation and hence momentum flux of the eddies. Although the interannual AAM fluctuations are initiated in the tropics, the driving waves for these persistent poleward-migrating anomalies originate in the extratropics of each hemisphere where there is a vigorous source of equatorward-propagating transient eddies with a broad spectrum of phase speeds (Fig. 3b). These eddies are known to propagate primarily equatorwards towards the latitude where the jet wind speed matches their phase speed, dissipating as they approach this critical latitude and thereby retarding the mean westerly flow25,26. Any perturbation to the axial angular momentum and hence the jet causes a displacement in the latitude of the critical lines and hence the latitude of the wave driving of the mean flow (Fig. 3c). A dipole anomaly in the wave driving either side of the perturbation results, which accelerates the perturbation on its poleward side. Similar to other wave-driven phenomena of this kind, such as the quasi-biennial oscillation27 and sudden stratospheric warmings28, the anomalies therefore migrate towards the source of driving waves (Fig. 3d). Eventually, they terminate at the wave source near 50° in the jet core in the extratropics of both hemispheres as is shown in Fig. 2.
a, Predicted anomalies in AAM (black, 1024 kg m2 s−1) and wave-driven acceleration (blue, 10−4 m s−2) from all waves (solid) and stationary waves (dotted) as a function of latitude, for the difference between the highest and lowest predicted AAM years. Anomalies are plotted from late spring/early summer (April–June) when ENSO anomalies decline to zero and the direct effect of ENSO from the tropics is small. Note how the wave driving accelerates the flow on the poleward side of the AAM anomaly in each hemisphere and how the stationary wave component is small compared with the total, implying that transient waves supply most of the wave-driven body force. b–d, A schematic of the wave-driven poleward propagation process for a positive perturbation to the AAM and zonal winds. b, The climatological jets (dashed line), spectrum of transient waves (wavy lines), climatological eddy momentum flux convergence (red) and divergence (blue). c,d, Initial perturbed jets and anomalies in eddy momentum flux divergence (c) and as the jet perturbation migrates poleward (d). Note that the same mechanism operates if the sign of anomalies is reversed.
Predictability of extratropical climate
Having established predictability of global AAM fluctuations and the link to meteorological fields, we now show that this mechanism provides predictability of the extratropical atmosphere. Signatures of increased AAM associated with the positive phase of the North Atlantic Oscillation (NAO) have previously been found in observations29. In addition, predictions of the NAO have been shown to be skilful a season ahead in the model used here12, and some skill persists for predictions of the NAO at lead times of a year14. Is it possible, therefore, that the AAM predictability shown here could be responsible for some of this long-range predictability of surface climate? Fig. 4 shows that correlations between predicted AAM and key aspects of the subsequent observed winter climate in the Atlantic and Pacific basins are significant out to a year ahead and persist throughout the forecast year. The correlations also show the characteristic poleward propagation seen in the AAM anomalies themselves, confirming that at each lead time into the forecast, as the AAM anomaly slowly approaches the extratropics, it is a statistically significant predictor of aspects of the following observed winter climate. The correlation between the average value of predicted AAM along the straight line of best fit through the correlations in Fig. 4 and the subsequent observed boreal winter NAO is 0.4 and is highly statistically significant (P < 0.01). This is larger than the correlation between ENSO and the NAO and similar to the NAO prediction skill at a one-year lead time14. Figure 4b shows a similar plot for Pacific jet-stream winds in the extratropics. Again, a statistically significant link is present at lead times of one year,and again, the correlations between predicted AAM and subsequent variations are significant (similar results hold for the Atlantic jet). The slow poleward propagation of AAM anomalies and their high predictability are therefore skilful indicators of extratropical climate at lead times over a year ahead.
a,b, Correlation between the ensemble mean predicted AAM (from forecasts started in November) and the following observed winter NAO (a) and Pacific jet-stream winds (b). Forecasts were started in November, and the NAO and jet-stream winds are predicted at a lead time of 13 months for all years between 1960 and 2017, inclusive. The NAO is the two-point difference in sea-level pressure between the Azores and Iceland, and the jet-stream wind is the zonal mean wind at 300 hPa and 60° N averaged over the Pacific (150° E to 150° W). The correlation with the following winter NAO and winds is plotted at each latitude and for each month as the forecasts progress. Positive correlations indicate that AAM anomalies precede the same-sign NAO and winds in the following winter as expected. Note the poleward migration with lead time (months), consistent with predictability arising from the poleward-migrating AAM anomalies. Hatching shows regions where the correlation between AAM and NAO is significant at the 90% level according to a one-sided t test.
Long-range prediction skill of the atmosphere, especially in the tropics, is thought to originate mainly from predicted ocean conditions. Similarly, ENSO often triggers the anomalous atmospheric angular momentum17,18,19 studied here and explains about half (though not all) of the year-to-year variance (r2 ≈ 0.5) in AAM at the start of the forecasts as explained above. In this Article, we have shown that these AAM anomalies are actually predictable at long lead times through a predictable atmospheric forcing mechanism that continues after the triggering ENSO anomalies have declined to zero. We have also shown that they precede important changes in extratropical climate. The poleward propagating signals found here are slower than some of the examples studied in observations21, and more work to understand the timescale of poleward propagation and, for example, the role of advection by the mean meridional flow would be useful. Nevertheless, these results present a source of long-range predictability that is often triggered by ENSO but subsequently resides within the atmosphere. Our analysis also helps to explain earlier findings of a stronger link between the extratropical atmosphere and ENSO in the winter following ENSO events than during concurrent winters30,31. We also note that use of AAM as a predictor achieves a level of skill at the one-year lead time similar to that of ensemble forecasts with four times as many members14, providing a diagnostic to interpret impending signals in operational near-term climate predictions and a focus for research into the signal-to-noise problems that necessitate the use of large ensembles in current prediction systems32.
Transient eddy driving of the zonal flow is an internal atmospheric process, and so given the link with long-range predictability shown here, the improved representation of transient eddy momentum fluxes in higher resolution climate models33,34 is likely to improve long-range predictions of the atmosphere. Finally, this source of predictability is analogous to other phenomena driven by wave–mean flow interaction such as sudden stratospheric warmings and the quasi-biennial oscillation27,28 that also provide long-range predictability. However, in the case analysed here, long-range predictability is provided by slow horizontal rather than vertical migration of zonal flow anomalies.
Methods
Model predictions
Our predictions of AAM are derived from the fourth decadal prediction system of the Met Office Hadley Centre (DePreSys4). This system uses the HadGEM3 global climate model37 at a resolution of 0.83° longitude and 0.53° latitude in the atmosphere and 0.25° in both latitude and longitude in the ocean. Forecasts are initialized with observational analyses of the ocean and atmosphere on 1 November each year as recommended for decadal climate predictions38. Members differ by ocean initial conditions from an ensemble of observational ocean analyses and the application of stochastic physics at each model time step. Ensemble predictions of ten members were initialized each year from 1960 and run out to ten years ahead.
AAM and length of day
The AAM is calculated at each time step and for each latitude, integrating through the depth of the atmosphere to the model lid at 85 km. The global AAM is calculated as follows:
where ρ is the atmospheric density, λ is longitude, φ is latitude, U is the zonal wind, r is radial distance from Earth’s centre, a is the radius of Earth and Ω is the mean angular velocity of Earth. Monthly means were then stored for each month, each forecast member and each start year. For comparison with observed values, the model fluctuations in AAM, ∆AAM, are converted to fluctuations in length of day τ assuming a constant moment of inertia I for the solid Earth of 8 × 1037 kg m2 and using the relation:
Observations
Length-of-day observations are from radio telescope observations analysed by the International Earth Rotation and Reference Systems Service. We use the service’s dataset 14 CO4, which provides monthly mean values from 1962 onwards when comprehensive data became available. Data have an accuracy of order 10−5 s. As is standard practice in long-range climate prediction, we removed the mean annual cycle to avoid artificially high prediction scores simply from predicting the annual cycle. We also removed low-frequency multidecadal variations using a five-year running mean to reveal the interannual anomalies shown in Fig. 1. Raw data are available from the IERS39.
The AAM from reanalysis was calculated from the ERA datasets35,36 using the preceding method. The NAO is calculated as the grid-point difference in sea-level pressure between the Azores and Iceland using the HadSLP2 dataset40. ENSO is measured by the Niño3.4 index from the HadISST2 dataset41.
Data availability
Atmospheric angular momentum data from the model predictions are available from https://doi.org/10.5281/zenodo.7003975. Observed length-of-day data are available from https://www.iers.org/IERS/EN/Home/home_node.html.
Code availability
The code we used to calculate atmospheric angular momentum is available from https://zenodo.org/record/7003975.
References
Rosen, R. D. The axial angular momentum balance of Earth and its fluid envelope. Surv. Geophys. 14, 1–29 (1993).
Munk, W. H. & McDonald, G. J. F. The Rotation of the Earth (Cambridge Univ. Press, 1960).
Barnes, R. T. H., Hide, R., White, A. A. & Wilson, C. A. Atmospheric angular momentum fluctuations, length of day changes and polar motion. Proc. R. Soc. Lond. A 387, 31–73 (1983).
Hide, R. & Dickey, J. O. Earth’s variable rotation. Science 253, 629–637 (1991).
Langley, R. B., King, R. W., Shapiro, I. I., Rosen, R. D. & Salstein, D. A. Atmospheric angular momentum and the length of day: a common fluctuation with a period near 50 days. Nature 294, 730–732 (1981).
Weickmann, K. M., Kiladis, G. N. & Sardeshmukh, P. D. The dynamics of intraseasonal atmospheric angular momentum oscillations. J. Atmos. Sci. 54, 1445–1461 (1997).
Dill, R., Dobslaw, H. & Thomas, M. Improved 90-day Earth orientation predictions from angular momentum forecasts of atmosphere, ocean, and terrestrial hydrosphere. J. Geod. 93, 287–295 (2019).
Bendick, R. & Bilham, R. Do weak global stresses synchronize earthquakes? Geophys. Res. Lett. 44, 8320–8327 (2017).
James, I. N. & Dodd, J. P. A mechanism for the low‐frequency variability of the mid‐latitude troposphere. Q. J. R. Meteorol. Soc. 122, 1197–1210 (1996).
Lee, S., Son, S.-W., Grise, K. & Feldstein, S. B. A mechanism for poleward propagation of zonal mean flow anomalies. J. Atmos. Sci. 64, 849–868 (2007).
Chemke, R. & Kaspi, Y. Poleward migration of eddy-driven jets. J. Adv. Model. Earth Syst. 7, 1457–1471 (2015).
Scaife, A. A. et al. Skillful long‐range prediction of European and North American winters. Geophys. Res. Lett. 41, 2514–2519 (2014).
MacLachlan, C. et al. Global Seasonal forecast system version 5 (GloSea5): a high‐resolution seasonal forecast system. Q. J. R. Meteorol. Soc. 141, 1072–1084 (2015).
Dunstone, N. et al. Skilful predictions of the winter North Atlantic Oscillation one year ahead. Nat. Geosci. 9, 809–814 (2016).
Smith, D. M. et al. North Atlantic climate far more predictable than models imply. Nature 583, 796–800 (2020).
Knight, J. R. et al. Predictions of climate several years ahead using an improved decadal prediction system. J. Clim. 27, 7550–7567 (2014).
Chao, B. F. Interannual length of day variation with relation to the Southern Oscillation/El Niño. Geophys. Res. Lett. 11, 541–544 (1984).
Dickey, J. O., Marcus, S. L. & Hyde, R. Global propagation of interannual fluctuations in atmospheric angular momentum. Nature 357, 484–488 (1992).
de Viron, O. & Dickey, J. O. The two types of El-Niño and their impacts on the length of day. Geophys. Res. Lett. 41, 3407–3412 (2014).
Swinbank, R. The global atmospheric angular momentum balance inferred from analyses made during FGGE. Q. J. R. Meteorol. Soc. 111, 977–992 (1985).
Feldstein, S. B. An observational study of the intraseasonal poleward propagation of zonal mean flow anomalies. J. Atmos. Sci. 55, 2516–2529 (1998).
James, I. N. & James, P. M. Spatial structure of ultra‐low‐frequency variability of the flow in a simple atmospheric circulation model. Q. J. R. Meteorol. Soc. 118, 1211–1233 (1992).
Karoly, D. J. The role of transient eddies in low‐frequency zonal variations of the Southern Hemisphere circulation. Tellus A 42, 41–50 (1990).
Edmon, H. J., Hoskins, B. J. & McIntyre, M. E. Eliassen–Palm cross sections for the troposphere. J. Atmos. Sci. 37, 2600–2616 (1980).
Randel, W. J. & Held, I. M. Phase speed spectra of transient eddy fluxes and critical layer absorption. J. Atmos. Sci. 48, 688–697 (1991).
Robinson, W. A. A baroclinic mechanism for the eddy feedback on the zonal index. J. Atmos. Sci. 57, 415–422 (2000).
Lindzen, R. S. & Holton, J. R. A theory of the quasi-biennial oscillation. J. Atmos. Sci. 25, 1095–1107 (1968).
Matsuno, T. A dynamical model of the stratospheric sudden warming. J. Atmos. Sci. 28, 1479–1494 (1971).
Baldwin, M. P. Annular modes in global daily surface pressure. Geophys. Res. Lett. 28, 4115–4118 (2001).
Ren, R. et al. Observational evidence of the delayed response of stratospheric polar vortex variability to ENSO SST anomalies. Clim. Dyn. 38, 1345–1358 (2012).
Okumura, Y. M., DiNezio, P. & Deser, C. Evolving impacts of multiyear La Niña events on atmospheric circulation and US drought. Geophys. Res. Lett. 44, 11–614 (2017).
Scaife, A. A. & Smith, D. A signal-to-noise paradox in climate science. NPJ Clim. Atmos. Sci. 1, 28 (2018).
Held, I. M. & Phillipps, P. Sensitivity of the eddy momentum flux to meridional resolution in atmospheric GCMs. J. Clim. 6, 499–507 (1993).
Scaife, A. A. et al. Does increased atmospheric resolution improve seasonal climate predictions? Atmos. Sci. Lett. 20, e922 (2019).
Uppala, S. M. et al. The ERA‐40 re‐analysis. Q. J. R. Meteorol. Soc. 131, 2961–3012 (2005).
Dee, D. P. et al. The ERA‐Interim reanalysis: configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 137, 553–597 (2011).
Williams, K. D. et al. The Met Office Global Coupled model 3.0 and 3.1 (GC3.0 and GC3.1) configurations. J. Adv. Model. Earth Syst. 10, 357–380 (2017).
Boer, G. J. et al. The Decadal Climate Prediction Project (DCPP) contribution to CMIP6. Geosci. Model Dev. 9, 3751–3777 (2016).
International Earth Rotation and Reference Systems Service: https://www.iers.org/IERS/EN/Home/home_node.html
Allan, R. & Ansell, T. A new globally complete monthly historical gridded mean sea level pressure dataset (HadSLP2): 1850–2004. J. Clim. 19, 5816–5842 (2006).
Titchner, H. A. & Rayner, N. A. The Met Office Hadley Centre sea ice and sea surface temperature data set, version 2: 1. Sea ice concentrations. J. Geophys. Res. Atmos. 119, 2864–2889 (2014).
Acknowledgements
This work was supported by the UK–China Research & Innovation Partnership Fund through the Met Office Climate Science for Service Partnership (CSSP) China as part of the Newton Fund (A.A.S., N.J.D., S.C.H., M.A.). A.A.S., L.H., N.J.D., S.C.H. and D.S. were also supported by the Met Office Hadley Centre Climate Programme funded by BEIS and Defra and by the European Commission Horizon 2020 EUCP project (GA 776613). A.A.S. was also supported by the Natural Environment Research Council NE/S004645/1. H.-L.R. is sponsored by the China National Key Research and Development Program on Monitoring, Early Warning and Prevention of Major Natural Disaster (2018YFC1506004), and A.v.N. was supported by the Met Office Weather and Climate Science for Service Partnership (WCSSP) India as part of the Newton Fund.
Author information
Authors and Affiliations
Contributions
A.A.S. led the study and carried out the analysis of the data. L.H. ran the climate model predictions. A.V.N. produced the observed angular momentum from reanalysis. M.A. provided code to calculate the EP fluxes. M.P.B., S.B., P.B., R.E.C., N.J.D., R.G., S.C.H., S.I., J.K., Y.N., H.-L.R. and D.S. provided constructive criticism, ideas and additional analysis as the work evolved, and all helped to write the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Geoscience thanks Robert Dill, David Straus and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Tom Richardson, in collaboration with the Nature Geoscience team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Scaife, A.A., Hermanson, L., van Niekerk, A. et al. Long-range predictability of extratropical climate and the length of day. Nat. Geosci. 15, 789–793 (2022). https://doi.org/10.1038/s41561-022-01037-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41561-022-01037-7
This article is cited by
-
Skillful prediction of length of day one year ahead in multiple decadal prediction systems
npj Climate and Atmospheric Science (2024)
-
Assessment of length-of-day and universal time predictions based on the results of the Second Earth Orientation Parameters Prediction Comparison Campaign
Journal of Geodesy (2024)