Abstract
Rapid ice loss from the Greenland ice sheet since 1992 is due in equal parts to increased surface melting and accelerated ice flow. The latter is conventionally attributed to ocean warming, which has enhanced submarine melting of the fronts of Greenland’s marine-terminating glaciers. Yet, through the release of ice sheet surface meltwater into the ocean, which excites near-glacier ocean circulation and in turn the transfer of heat from ocean to ice, a warming atmosphere can increase submarine melting even in the absence of ocean warming. The relative importance of atmospheric and oceanic warming in driving increased submarine melting has, however, not been quantified. Here, we reconstruct the rate of submarine melting at Greenland’s marine-terminating glaciers from 1979 to 2018 and estimate the resulting dynamic mass loss. We show that in south Greenland, variability in submarine melting was indeed governed by the ocean, but, in contrast, the atmosphere dominated in the northwest. At the ice sheet scale, the atmosphere plays a first-order role in controlling submarine melting and the subsequent dynamic mass loss. Our results challenge the attribution of dynamic mass loss to ocean warming alone and show that a warming atmosphere has amplified the impact of the ocean on the Greenland ice sheet.
Similar content being viewed by others
Main
Ocean forcing is understood to have driven half of the mass loss from the Greenland ice sheet during 1992–20181,2,3, leading to the ice sheet’s contribution to global sea level rise increasing from 5% in 1993 to 25% in 20144. Ocean forcing manifests as melting of the submerged fronts of Greenland’s marine-terminating glaciers (submarine melting) and can result in glacier retreat and acceleration either directly or by increasing the rate of iceberg production5,6,7.
The rate of submarine melting is controlled both by the heat content of the ocean near the glacier and by the turbulent processes that flux heat from the ocean into the ice8,9. These turbulent processes are strongly influenced by vigorous upwelling of ocean waters in buoyant plumes adjacent to the ice, driven by the release of fresh subglacial discharge from beneath the glacier (Fig. 1)10,11. In turn, subglacial discharge is sourced largely from atmospheric-driven melting of the ice sheet surface12. Thus, submarine melting experiences both oceanic and atmospheric influences (Fig. 1), with oceanic variability controlling the heat available for melting and atmospheric variability determining to a large extent how much of the heat is actually used.
Freshwater emerging from beneath marine-terminating glaciers (subglacial discharge) drives vigorous upwelling plumes. Subglacial discharge can be sourced either from surface melting or frictional melting at the bed. Plumes entrain warm fjord waters, which are replenished by the ocean and fjord circulation processes. The combination of fast-moving and warm water in the plume drives melting of submerged ice at the glacier terminus (submarine melting). By the described chain of processes, submarine melting is influenced by both atmospheric and oceanic variability.
The relative importance of atmospheric and oceanic sources of variability to submarine melting and the subsequent ice sheet dynamic mass loss has, however, not been quantified. The prevailing view is that submarine melt rate variability and the consequent impact on marine-terminating glacier dynamics result predominantly from changes in the ocean1,3,5,13, but previous work has either been limited to individual glaciers, or has not accounted for or not isolated the atmospheric influence on submarine melting. This limits our understanding of the fundamental sensitivity of the ice sheet to climate warming and restricts our ability to project future change.
Here, we use observations and reanalysis of the atmosphere and ocean to reconstruct submarine melt rates at Greenland’s marine-terminating glaciers over a 40-year period from 1979 to 2018. We isolate variability driven by the atmosphere and ocean respectively and force a two-stage glacier model with the resulting time series to estimate the impact on ice sheet dynamic mass loss. Our findings suggest that atmospheric variability is nearly as important as oceanic variability to submarine melting at the ice sheet scale and is dominant in some regions, challenging the paradigm that equates Greenland’s dynamic mass loss with ocean variability alone.
Submarine melting of Greenland’s marine-terminating glaciers
We quantify plume-driven submarine melt rate, \(\dot{m}\), for 123 marine-terminating glaciers around the ice sheet as \(\dot{m}=0.142\,{Q}^{0.31}\,{{{\mbox{TF}}}}^{1.19}\), in which Q is the subglacial discharge arising from both surface melting and frictional melting at the bed and TF is the ocean thermal forcing, defined as the difference between the in situ ocean temperature and freezing point (Methods and Extended Data Fig. 3). While there exists substantial uncertainty regarding the absolute values predicted by the parameterization9, the form of the parameterization, which dictates the relative change in melt rates used in this study, has extensive support from theory14,15, observations10,16,17,18 and modelling19,20. Subglacial discharge arising from surface melting is estimated by summing the surface meltwater volume, as simulated by the regional climate model RACMO21, over the subglacial hydrological catchment of the glacier22 (Methods). The assumption that the majority of surface meltwater enters the fjord subglacially is supported by a high moulin and crevasse density at the margin of the ice sheet23 and by studies that find agreement between RACMO-estimated subglacial discharge and plume freshwater content10,17. Discharge from melting at the ice sheet bed is assumed constant and is estimated following ref. 24. Ocean thermal forcing is estimated using a multi-model mean of the ocean reanalyses ASTE_R1, ORAS5 and CHORE_RL25,26,27 and the observational dataset EN.4.2.128, with properties extrapolated into fjords from the nearest available values on the continental shelf, taking into account fjord bathymetry (Methods). Given the seasonality of both subglacial discharge (Extended Data Fig. 1) and ocean thermal forcing (Extended Data Fig. 2), we estimate monthly submarine melt rate using monthly subglacial discharge and monthly ocean thermal forcing before averaging over each year from 1979 to 2018. When splitting out variability in submarine melting driven by the atmosphere or ocean we allow one factor to vary while holding the other constant at its mean 1979–1993 value (Supplementary Information).
Spatial variability in submarine melting
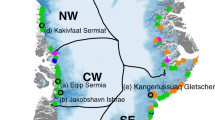
The 40-year mean annual submarine melt estimate shows that at the ice sheet scale, spatial variability in submarine melting is controlled to first order by the distribution of ocean heat governed by the large-scale ocean circulation (Fig. 2a). The highest melt rates are found in south Greenland where glaciers and fjords have ready access to warm Atlantic waters from the Irminger Sea. There is a marked latitudinal gradient in submarine melting along west Greenland north of the Davis Strait, with melt rates declining with increasing distance from the warm source waters in the south. Even more pronounced is the gradient across Denmark Strait, meaning that glaciers in northeast Greenland experience much colder ocean waters and relatively little submarine melting. Glaciers in north Greenland, farthest from the source of warm water, experience the coldest ocean and least submarine melting of all (Fig. 2a).
a, Ocean thermal forcing (shaded areas) at the ocean bottom or 1000 m (whichever is shallower) and annual submarine melt rate (filled squares) at Greenland’s marine-terminating glaciers. The black dotted line shows the 1,000 m isobath and delineates the extent of the continental shelf. The black dashed regions on the ice sheet delineate the hydrological catchments for three large example glaciers: Jakobshavn Isbrae (JI), Helheim (HH) and Kangerdlugssuaq (KG). The five ice sheet regions considered throughout the paper—south (SO), central-west (CW), northwest (NW), northeast (NE) and north (NO)—are delineated by the black ticks. Other labels are the Irminger Sea (Irm), Davis Strait (Dav) and Denmark Strait (Den). Bathymetry is from ref. 42 and ref. 43. b, Subglacial discharge (x axis, note logarithmic scale) and ocean thermal forcing (y axis) for each marine-terminating glacier. The background shading shows the resulting submarine melt rate. Glaciers are coloured by their regional grouping. The larger squares and error bars show the median and interquartile range for each region, respectively. c, Submarine melt rate versus grounding line depth by region with fitted linear trends (all significant at the 5% level) as dashed lines. All the results shown in these plots are annually averaged over 1979–2018.
Grouping of the glaciers into five regions shows that submarine melt rate varies within a region due to order-of-magnitude differences in subglacial discharge and smaller differences in ocean thermal forcing (Fig. 2b). Variability in subglacial discharge is linked to hydrological catchment size, and there exist statistically significant relationships between ocean thermal forcing and grounding line depth (Extended Data Fig. 5), and submarine melt rate and grounding line depth, in each region (Fig. 2c). As a rule, annual submarine melt rate increases by 0.2 to 0.4 m d−1 for every 100 m of grounding line depth. Therefore, although grounding line depth does not appear explicitly in the submarine melt rate parameterization, it plays an important role in determining glacier-to-glacier variability in submarine melt rate within a region.
Temporal variability in submarine melting
Annual submarine melt rate increased in all regions from the 1990s to peak in the 2000s at 13–50% above 1979–1993 mean values (Fig. 3a–d, black). Since the 2000s, melt rates have decreased but have not returned to pre-1990s values. Note that here we highlight only the three regions that dominate Greenland’s dynamic sea level contribution (south, central-west and northwest Greenland); northeast and north Greenland are described in the Extended Data Figs. 6 and 7.
a–d, Regional percentage change in annual submarine melt rate relative to the 1979–1993 mean accounting for only atmospheric variability (solid blue), accounting for only oceanic variability (solid red) and accounting for both atmospheric and oceanic variability (solid black) for SO (a), CW (b), NW (c) and all Greenland (d). e–h, Percentage change in annual subglacial discharge (blue) and annual ocean thermal forcing (red) relative to the 1979–1993 mean for SO (e), CW (f), NW (g) and all Greenland (h). In all plots the lines show the median value over all marine-terminating glaciers in the region, while the shading shows the interquartile range. The fact that this shading is relatively narrow shows that all glaciers in a region experience similar variability in forcing. All time series have been smoothed using a ten-year window. Equivalent plots for the two ice sheet regions not highlighted here are given in Extended Data Fig. 6.
The dominant driver of change in submarine melt rate varies by region and is revealed by allowing only the atmosphere or ocean to vary while holding the other constant. In south and central-west Greenland, ocean variability alone explains most of the change in submarine melt rate (Fig. 3a,b). The rapid increase in submarine melting from the mid-1990s in these regions was driven almost exclusively by increased ocean thermal forcing, and even high subglacial discharge during the 2010s has played only a minor role (Fig. 3e,f). By contrast, in northwest Greenland atmospheric and oceanic variability seem to be approximately equally important to the evolution of submarine melt rate (Fig. 3c). The importance of the atmosphere in this region results from the dramatic increase in subglacial discharge beginning in 2000 relative to the much more muted increase in ocean thermal forcing (Fig. 3g).
For Greenland as a whole, the ocean seems to be more important in controlling submarine melting, especially during the 1990s, but the atmosphere has played a substantial role, especially since 2000 (Fig. 3d,h). For example, the ten-year smoothed submarine melt rate in 2010 was 22% above the 1979–1993 value, but only three-fifths of this elevated value can be accounted for by the ocean alone.
Impact on dynamic mass loss
We assess the impact of submarine melting on Greenland’s marine-terminating glaciers using a simple two-stage model that has been shown to reliably capture a glacier’s dynamic response to external forcing when compared to more complex models29,30. The model accounts for terminus ice loss due to submarine melting and the subsequent potential amplification of calving. For each of the 123 glaciers, we run the model forwards from 1979 holding surface mass balance constant and assuming a linear prograde bed slope, but imposing the three submarine melt rate time series (atmosphere only, ocean only, both vary). We generate a large ensemble of simulations by varying all remaining free parameters (Methods), which control the timescale and magnitude of the glacier’s dynamic response. Lastly, we group the simulations by ice sheet region. We strongly emphasize that due to their simplicity, particularly regarding geometry and their neglect of forcings beyond submarine melting, these simulations are not intended to accurately simulate any individual glacier. Instead, these simulations quantify the dynamic response to submarine melt rate of an idealized glacier located in a given region of the ice sheet, essentially providing a mapping from submarine melt rate (Fig. 3a–d) to retreat and dynamic sea level contribution.
All simulations show retreat and a positive dynamic sea level contribution in response to increased submarine melting (Fig. 4). In south and central-west Greenland, simulations in which submarine melt rate fluctuates only due to oceanic variability give ~75% of the retreat and dynamic sea level contribution compared with simulations in which both atmospheric and oceanic variability are considered (Fig. 4a,b,e,f), consistent with the limited importance of atmospheric variability to the submarine melt rate (Fig. 3a,b). Conversely, in northwest Greenland, atmospheric-sourced variability in submarine melting alone explains ~60% of retreat and dynamic sea level contribution, with oceanic variability playing a lesser role (Fig. 4c,g), once more consistent with the greater importance of the atmosphere to submarine melting in northwest Greenland (Fig. 3c). There is only little sensitivity of these percentages to the choice of a particular ocean reanalysis product, except in northwest Greenland where use of only the ORAS5 dataset would suggest an even greater role for the atmosphere (Extended Data Fig. 10). At the ice sheet scale, oceanic-sourced variability in submarine melting alone accounts for ~70% of retreat and dynamic sea level contribution (Fig. 4d,h), such that atmospheric-sourced variability in submarine melting (which accounts for the remainder) has played a substantial amplifying role in glacier retreat and ice sheet dynamic mass loss.
a–h, The results are obtained by forcing a simple glacier model ensemble with the submarine melt rate variability shown in Fig. 3. Each plot contains the scenario in which only the atmosphere varies (blue), only the ocean varies (red) and both vary (black) for SO (a, e), CW (b, f), NW (c, g) and all Greenland (d, h). The results are normalized by the retreat (a–d) or sea level contribution (e–h) by 2018 when both atmosphere and ocean vary. The shading shows the interquartile range of results obtained by varying parameters in the model, while the solid lines show the ensemble median. The retreat and sea level time series have been smoothed using four- and one-year windows, respectively. Additional plots showing the regions not highlighted here, retreat observations and ice discharge are given in Extended Data Figs. 7-9.
Interplay of atmospheric and oceanic variability
The relative importance of atmospheric and oceanic sources of variability in submarine melting to ice sheet dynamic mass loss (Fig. 1) is determined firstly by how these factors combine in the submarine melt rate parameterization, secondly by their observed relative variability (Figs. 2 and 3) and thirdly by the sensitivity of glaciers to submarine melting (Fig. 4). Owing to plume dynamics and the physics of heat transfer from ocean to ice, the melt rate parameterization contains the subglacial discharge and ocean thermal forcing raised to the power 0.31 and 1.18, respectively. Thus, submarine melt rate is approximately four times more sensitive to equivalent variability in ocean thermal forcing than subglacial discharge. Yet, in all regions, the relative increase in subglacial discharge from the 1990s into the 2000s is larger than for the thermal forcing, dramatically so in northwest Greenland (Fig. 3e–h). Once the glacier model is forced by these submarine melt rate time series, seasonality also modulates the relative importance of atmosphere and ocean. The increased subglacial discharge from a warming atmosphere manifests as rapid submarine melting during summer but makes little difference during winter, while the impact of a warming ocean is felt year-round. In our simple simulations the glaciers seem to be particularly sensitive to rapid summer melting, lending greater importance to atmospheric-sourced variability than might be expected from examining submarine melt rates alone (Figs. 3 and 4).
In sum, our results show that the retreat and speed-up of Greenland’s marine-terminating glaciers over past decades was a result of a combination of atmospheric and oceanic variability whose relative role varied by sector: in south and central-west Greenland it was largely a result of ocean warming, while in northwest Greenland the atmosphere played the greater role (Fig. 4). We suggest that these regional differences arise from the same large-scale atmospheric and oceanic circulations that explain spatial variability in submarine melting (Fig. 2). South Greenland is directly exposed to North Atlantic Ocean variability1, while northwest Greenland sees only a muted signal because waters lose much of their heat as they travel up the west coast of Greenland (Fig. 2)3,13,31,32. Similarly, owing to Arctic amplification and a differing cloud response to large-scale atmospheric changes, northern Greenland has seen greater relative increases in air temperature and subglacial discharge than southern Greenland, although changes in the south remain larger in an absolute sense33. Our conclusions for northwest Greenland are comparable to ref. 34, which found that marine-terminating glaciers on the other side of Baffin Bay in Arctic Canada have primarily responded to atmospheric temperature.
The primary implication of our results is that a full understanding of submarine melting and its impacts requires careful accounting for both atmospheric and oceanic change, particularly as large-scale circulation ensures that these changes may not be coupled either in space or in time. For example, global climate models project nuanced and regionally variable ocean warming over the coming century35,36,37,38. Yet the same models, once downscaled using regional climate models, also project vast, ice-sheet-wide increases in subglacial discharge38,39,40 that may amplify or overwhelm ocean-sourced variability in submarine melting, leading to the possibility that submarine melt rates could continue to increase and drive glacier retreat even if for some regions or time periods the ocean has not warmed. The sea level implication is clearly most relevant to regions of the ice sheet that are exposed to the ocean through many tidewater glaciers, such as southeast and northwest Greenland41.
The dynamics of plumes at Greenland’s tidewater glaciers ensure that atmospheric variability is a first-order control on submarine melting and the associated glacier retreat and dynamic mass loss. A simple glacier model suggests that, without concurrent atmospheric warming, the retreat and dynamic sea level contribution of Greenland’s marine-terminating glaciers would have been reduced by around a third (and by nearly a half in northwest Greenland). If we are to attribute the recent dramatic retreat and acceleration of Greenland’s marine-terminating glaciers to increased submarine melting, then this is due to a warming of both the atmosphere and ocean. As such, the atmosphere has substantially amplified the response of the ice sheet to ocean warming and will likely continue to do so over the coming century.
Methods
Only a brief description of the methods is given here. For full details, see the Supplementary Information.
Marine-terminating glaciers
To define the set of marine-terminating glaciers considered, we start from a list of Greenland’s 243 fastest-flowing glaciers provided in Table S1of ref. 43. To focus on marine-terminating glaciers, we remove 69 glaciers that are either land-terminating or effectively land-terminating (maximum grounding line depth <50 m). We also remove 41 glaciers for which the deepest path to the ocean crosses a point shallower than 25 m. These glaciers are either relatively isolated from the ocean, or if the bathymetry is inaccurate then we cannot reliably infer ocean properties for these glaciers. Lastly, we remove 10 glaciers with a mean annual subglacial discharge <2.5 m3 s−1. The final dataset of 123 marine-terminating glaciers (Fig. 2) contains 76 of Greenland’s fastest 100 glaciers43.
Subglacial discharge
We estimate monthly subglacial discharge for each marine-terminating glacier (Extended Data Fig. 1) by delineating its hydrological catchment and estimating surface runoff and basal melt rates following the method of ref. 22. The hydrological catchment is defined by performing flow routing44 on the subglacial hydropotential defined in terms of the bed topography and ice thickness according to BedMachine v343, and assuming a subglacial water pressure equal to the ice overburden pressure. Monthly surface runoff is obtained from the regional climate model RACMO2.3p221, while a constant basal melt rate is assumed following ref. 24. Subglacial discharge is then the sum of the surface and basal meltwater runoff over the hydrological catchment of the glacier. We assume that the catchments are stable throughout the time period and that little supraglacial redirection into neighbouring catchments occurs.
Ocean thermal forcing
In the absence of continuous, long-term oceanographic observations from a substantial number of glacial fjords around Greenland, we have used the ocean reanalysis and observational products ASTE_R1, ORAS5, CHORE_RL and EN.4.2.125,26,27,28 to quantify properties on Greenland’s continental shelf (for example, Fig. 2). For each glacier, we apply an algorithm similar to ref. 45 and ref. 38 to identify the deepest, closest water on the continental shelf that is able to access the calving front without being impeded by bathymetry (Extended Data Fig. 2). Note that we assign only a single grounding line temperature and salinity to the glacier rather than a full profile—we assume that owing to upwelling in the plume, this grounding line value is the most relevant for submarine melting of the glacier. Grounding line water properties are then converted to thermal forcing, defined as the difference between the in situ temperature and in situ freezing point, using the linearized freezing point equation of ref. 14. Because each of the four ocean products considered have different resolutions and bathymetry, the process is repeated separately for each product, and the resulting four time series are combined into a single time series by averaging over the data products to create a multi-model mean (Extended Data Fig. 2).
Submarine melt rate
Submarine melting induced by a plume can be parameterized in the form \(\dot{m}=\kappa \,{Q}^{\alpha }\,{{{\mbox{TF}}}}^{\beta }\), where κ, α and β are constants, Q is subglacial discharge and TF is ocean thermal forcing (for example, refs. 14,15,20). Note that within a discharge plume, submarine melt rate close to the grounding line is independent of terminus shape46 and so provided we consider melt rate close to the grounding line (as in this study), we can equally apply this parameterization at vertical or undercut fronts and at glaciers having an ice tongue or shelf. We take \(\dot{m}\) to be the maximum submarine melt rate in the plume and fix the constants κ, α and β by comparison to a standard buoyant plume model14,15 with a line plume geometry of width w (ref. 17), so that the subglacial discharge per unit width is then q = Q/w. We perform a parameter sweep over q, TF and grounding line depth and fit the parameterization to these simulations by least squares (Extended Data Fig. 3), obtaining \(\dot{m}=0.732\,{q}^{0.31}\,{{{\mbox{TF}}}}^{1.19}\). Note that beyond its effect on thermal forcing, grounding line depth only weakly impacts maximum submarine melt rate and so does not appear explicitly in the parameterization. Observations support a line plume width w ≈ 200 m (ref. 17) so that the final parameterization may be written in terms of the total subglacial discharge Q and thermal forcing TF as \(\dot{m}=0.142\,{Q}^{0.31}\,{{{\mbox{TF}}}}^{1.19}\). When splitting out variability due to atmosphere and ocean, we apply the same parameterization but hold one of the factors Q or TF constant at its mean 1979–1993 value.
Glacier model
To estimate the impact of variability in submarine melt rate on glacier retreat, ice discharge and mass loss we use a simple two-stage glacier model adapted from ref. 29, with the only difference to that study being the addition of submarine melt rate and calving amplification to the calving flux. The model consists of a glacier interior of length L, ice thickness H and surface mass balance P. The glacier interior delivers an ice flux Q to the terminus, which has ice thickness hg, while the grounding line/calving flux is Qg. Following ref. 29, mass conservation for the interior and terminus regions gives \(\frac{{\mathrm{d}}H}{{\mathrm{d}}t}=P-\frac{{Q}_{{\mathrm{g}}}}{L}-\frac{H}{{h}_{{\mathrm{g}}}L}\left(Q-{Q}_{{\mathrm{g}}}\right)\) and \(\frac{{\mathrm{d}}L}{{\mathrm{d}}t}=\frac{1}{{h}_{{\mathrm{g}}}}\left(Q-{Q}_{{\mathrm{g}}}\right)\) where t is time. The interior flux is estimated as \(Q=\nu \frac{{H}^{2n+1}}{{L}^{n}}\), in which n = 3 is the Glen’s flow law exponent and ν is a constant related to the basal friction. The grounding line/calving flux is written \({Q}_{{\mathrm{g}}}={{\varOmega }}{h}_{{\mathrm{g}}}^{\gamma }+(1+\theta )\dot{m}{h}_{{\mathrm{g}}}\), in which Ω is a constant related to the basal friction and ice softness, γ = 19/4 (ref. 47), \(\dot{m}\) is the submarine melt rate and θ is a calving multiplier. Finally, the terminus is assumed to be at flotation hg = −(ρw/ρi)bL, in which bL is the water depth at the terminus, ρw = 1,028 kg m−3 is the density of ocean water and ρi = 917 kg m−3 is the density of ice. The model applies equally to glaciers with an ice shelf, provided that the ice shelf provides little buttressing to flow, which is a simplifying assumption but affects very few of the glaciers in the dataset.
Glacier simulations
To initialize the glacier model we assume that during 1979–1993 the glacier is close to steady state (that is, the mean value of \(\frac{{\mathrm{d}}H}{{\mathrm{d}}t}\) and \(\frac{{\mathrm{d}}L}{{\mathrm{d}}t}\) during this period is 0). The model then has six remaining free parameters, which can be taken as initial ice velocity v0, initial calving front ice thickness hg0, initial inland ice thickness H0, initial glacier length L0, bed slope bx and calving rate multiplier θ. All constants in the glacier model can be expressed in terms of these parameters. Rather than trying to model a specific glacier, we instead test two representative values for each of these six free parameters (Supplementary Table 2), giving a set of 26 = 64 simulations for each submarine melt rate time series. With this initialization, the model is run forwards from 1979 to 2018, forced by monthly submarine melt rate from each glacier in the dataset. Surface mass balance is held constant throughout. We consider three submarine melt rate time series per glacier: atmosphere varies, ocean varies and both vary. We then have 64 simulations for each of 123 glaciers and for each of 3 submarine melt scenarios (total 23,616 simulations).
Analysis of simulations
The terminus position, L, is a direct output of the simulations while the cumulative sea level contribution per unit width of glacier in year t, SLR, is calculated as \(\,{{\mbox{SLR}}}\,=\int\nolimits_{1979}^{t}\left(PL-Q\right)\,{\mathrm{d}}{t}^{\prime}\). In order to facilitate comparison between simulations, we calculate normalized terminus position \(\tilde{L}=\frac{L-{L}_{0}}{{R}_{{\mathrm{b}}}}\), in which Rb is the total retreat between 1979 and 2018 obtained in the simulation with both atmospheric and oceanic variability in submarine melting. Similarly, sea level contribution is normalized as \(\tilde{\,{{\mbox{SLR}}}}=\frac{{{\mbox{SLR}}}}{{{{\mbox{SLR}}}}_{{\mathrm{b}}}}\), where SLRb is the total 1979–2018 sea level contribution in the simulation with both atmospheric and oceanic variability in submarine melting (Extended Data Fig. 4). By this normalization, all simulations that account for both atmospheric and ocean-sourced variability in submarine melting have a normalized retreat of −1 and a sea level contribution of 1 in 2018, while simulations accounting for only atmospheric or oceanic variability alone have a smaller normalized retreat and sea level contribution (Fig. 4). Lastly, simulations are grouped by ice sheet region.
Data availability
All the datasets produced by this work can be found at https://doi.org/10.5281/zenodo.7113992 and https://github.com/donaldaslater/slater_2022_submelt. This includes the final subglacial discharge, ocean thermal forcing and submarine melt rate time series for each of the 123 glaciers. Concerning the key datasets used, further details are given at the links above. Here we note that BedMachinev3 is available from the NSIDC at https://nsidc.org/data/idbmg4/versions/4. RACMO surface runoff data is available upon request from Brice Noël at B.P.Y.Noel@uu.nl. ASTE_R1 output may be downloaded from the UT Austin ECCO portal at https://web.corral.tacc.utexas.edu/OceanProjects/ASTE/. ORAS5 output may be downloaded from the Integrated Climate Data Center at https://www.cen.uni-hamburg.de/icdc/data/ocean/easy-init-ocean/ecmwf-oras5.html. CHORE_RL output may be obtained from the Centro Euro-Mediterraneo sui Cambiamenti Climatici at http://c-glors.cmcc.it/index/index.html. EN.4.2.1 output may be downloaded from the UK Met Office at https://www.metoffice.gov.uk/hadobs/en4/download-en4-2-1.html.
Code availability
All of the code required to reproduce this work and the plots may be found at https://github.com/donaldaslater/slater_2022_submelt and https://doi.org/10.5281/zenodo.7113992.
References
Straneo, F. & Heimbach, P. North Atlantic warming and the retreat of Greenland’s outlet glaciers. Nature 504, 36–43 (2013).
The IMBIE Team Mass balance of the Greenland ice sheet from 1992 to 2018. Nature 579, 233–239 (2020).
Wood, M. et al. Ocean forcing drives glacier retreat in Greenland. Sci. Adv. 7, eaba7282 (2021).
Chen, X. et al. The increasing rate of global mean sea-level rise during 1993–2014. Nat. Clim. Change 7, 492–495 (2017).
Holland, D. M., Thomas, R. H., de Young, B., Ribergaard, M. H. & Lyberth, B. Acceleration of Jakobshavn Isbrae triggered by warm subsurface ocean waters. Nat. Geosci. 1, 659–664 (2008).
O’Leary, M. & Christoffersen, P. Calving on tidewater glaciers amplified by submarine frontal melting. Cryosphere 7, 119–128 (2013).
Catania, G. A., Stearns, L. A., Moon, T. A., Enderlin, E. M. & Jackson, R. H. Future evolution of Greenland’s marine-terminating outlet glaciers. J. Geophys. Res. Earth Surf. 125, e2018JF004873 (2020).
Holland, D. M. & Jenkins, A. Modeling thermodynamic ice-ocean interactions at the base of an ice shelf. J. Phys. Oceanogr. 29, 1787–1800 (1999).
Sutherland, D. A. et al. Direct observations of submarine melt and subsurface geometry at a tidewater glacier. Science 365, 369–374 (2019).
Mankoff, K. D. et al. Structure and dynamics of a subglacial discharge plume in a Greenlandic fjord. J. Geophys. Res. 121, 8670–8688 (2016).
Jackson, R. H. et al. Meltwater intrusions reveal mechanisms for rapid submarine melt at a tidewater glacier. Geophys. Res. Lett. 47, e2019GL085335 (2020).
Chu, V. W. Greenland ice sheet hydrology: a review. Prog. Phys. Geogr. Earth Environ. 38, 19–54 (2014).
Khazendar, A. et al. Interruption of two decades of Jakobshavn Isbrae acceleration and thinning as regional ocean cools. Nat. Geosci. 12, 277–283 (2019).
Jenkins, A. Convection-driven melting near the grounding lines of ice shelves and tidewater glaciers. J. Phys. Oceanogr. 41, 2279–2294 (2011).
Slater, D. A., Goldberg, D. N., Nienow, P. W. & Cowton, T. R. Scalings for submarine melting at tidewater glaciers from buoyant plume theory. J. Phys. Oceanogr. 46, 1839–1855 (2016).
Motyka, R. J., Dryer, W. P., Amundson, J., Truffer, M. & Fahnestock, M. Rapid submarine melting driven by subglacial discharge, LeConte Glacier, Alaska. Geophys. Res. Lett. 40, 5153–5158 (2013).
Jackson, R. H. et al. Near-glacier surveying of a subglacial discharge plume: implications for plume parameterizations. Geophys. Res. Lett. 44, 6886–6894 (2017).
Washam, P., Nicholls, K. W., Münchow, A. & Padman, L. Summer surface melt thins Petermann Gletscher ice shelf by enhancing channelized basal melt. J. Glaciol. 65, 662–674 (2019).
Xu, Y., Rignot, E., Fenty, I., Menemenlis, D. & Flexas, M. M. Subaqueous melting of Store Glacier, West Greenland from three-dimensional, high-resolution numerical modeling and ocean observations. Geophys. Res. Lett. 40, 4648–4653 (2013).
Rignot, E. et al. Modeling of ocean-induced ice melt rates of five west Greenland glaciers over the past two decades. Geophys. Res. Lett. 43, 6374–6382 (2016).
Noël, B. et al. Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 1: Greenland (1958–2016). Cryosphere 12, 811–831 (2018).
Slater, D. A. et al. Estimating Greenland tidewater glacier retreat driven by submarine melting. Cryosphere 13, 2489–2509 (2019).
Yang, K. & Smith, L. C. Internally drained catchments dominate supraglacial hydrology of the southwest Greenland ice sheet. J. Geophys. Res. Earth Surf. 121, 1891–1910 (2016).
Karlsson, N. B. et al. A first constraint on basal melt-water production of the Greenland ice sheet. Nat. Commun. 12, 3461 (2021).
Yang, C., Masina, S. & Storto, A. Historical ocean reanalyses (1900–2010) using different data assimilation strategies. Q. J. R. Meteorol. Soc. 143, 479–493 (2017).
Zuo, H., Balmaseda, M. A., Tietsche, S., Mogensen, K. & Mayer, M. The ECMWF operational ensemble reanalysis-analysis system for ocean and sea ice: a description of the system and assessment. Ocean Sci. 15, 779–808 (2019).
Nguyen, A. T. et al. The Arctic Subpolar gyre sTate Estimate: description and assessment of a data-constrained, dynamically consistent ocean-sea ice estimate for 2002–2017. J. Adv. Model. Earth Syst. 13, e2020MS002398 (2021).
Good, S. A., Martin, M. J. & Rayner, N. A. EN4: quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J. Geophys. Res. Oceans 118, 6704–6716 (2013).
Robel, A. A., Roe, G. H. & Haseloff, M. Response of marine-terminating glaciers to forcing: time scales, sensitivities, instabilities, and stochastic dynamics. J. Geophys. Res. Earth Surf. 123, 2205–2227 (2018).
Robel, A. A., Seroussi, H. & Roe, G. H. Marine ice sheet instability amplifies and skews uncertainty in projections of future sea-level rise. Proc. Natl Acad. Sci. USA 116, 14887–14892 (2019).
Zweng, M. M. & Munchow, A. Warming and freshening of Baffin Bay, 1916–2003. J. Geophys. Res. Oceans 111, C07016 (2006).
Myers, P. G., Kulan, N. & Ribergaard, M. H. Irminger water variability in the West Greenland Current. Geophys. Res. Lett. 34, 17601 (2007).
Noël, B., van de Berg, W. J., Lhermitte, S. & van den Broeke, M. R. Rapid ablation zone expansion amplifies north Greenland mass loss. Sci. Adv. 5, eaaw0123 (2019).
Cook, A. J. et al. Atmospheric forcing of rapid marine-terminating glacier retreat in the Canadian Arctic Archipelago. Sci. Adv. 5, eaau8507 (2019).
Yin, J. et al. Different magnitudes of projected subsurface ocean warming around Greenland and Antarctica. Nat. Geosci. 4, 524–528 (2011).
Barthel, A. et al. CMIP5 model selection for ISMIP6 ice sheet model forcing: Greenland and Antarctica. Cryosphere 14, 855–879 (2020).
Golledge, N. R. et al. Global environmental consequences of twenty-first-century ice-sheet melt. Nature 566, 65–72 (2019).
Slater, D. A. et al. Twenty-first century ocean forcing of the Greenland ice sheet for modelling of sea level contribution. Cryosphere 14, 985–1008 (2020).
Fettweis, X. et al. Estimating the Greenland ice sheet surface mass balance contribution to future sea level rise using the regional atmospheric climate model MAR. Cryosphere 7, 469–489 (2013).
Hofer, S. et al. Greater Greenland ice sheet contribution to global sea level rise in CMIP6. Nat. Commun. 11, 6289 (2020).
Goelzer, H. et al. The future sea-level contribution of the Greenland ice sheet: a multi-model ensemble study of ISMIP6. Cryosphere 14, 3071–3096 (2020).
Schaffer, J. et al. A global, high-resolution data set of ice sheet topography, cavity geometry, and ocean bathymetry. Earth Syst. Sci. Data 8, 543–557 (2016).
Morlighem, M. et al. BedMachine v3: complete bed topography and ocean bathymetry mapping of Greenland from multibeam echo sounding combined with mass conservation. Geophys. Res. Lett. 44, 11051–11061 (2017).
Schwanghart, W. & Scherler, D. TopoToolbox 2 - MATLAB-based software for topographic analysis and modeling in Earth surface sciences. Earth Surf. Dyn. 2, 1–7 (2014).
Morlighem, M., Wood, M., Seroussi, H., Choi, Y. & Rignot, E. Modeling the response of northwest Greenland to enhanced ocean thermal forcing and subglacial discharge. Cryosphere 13, 723–734 (2019).
Slater, D. A., Nienow, P. W., Goldberg, D. N., Cowton, T. R. & Sole, A. J. A model for tidewater glacier undercutting by submarine melting. Geophys. Res. Lett. 44, 2360–2368 (2017).
Schoof, C. Ice sheet grounding line dynamics: steady states, stability, and hysteresis. J. Geophys. Res. Earth Surf. 112, F03S28 (2007).
King, M. D. et al. Dynamic ice loss from the Greenland ice sheet driven by sustained glacier retreat. Commun. Earth Environ. 1, 1 (2020).
Acknowledgements
D.A.S. acknowledges support from NERC Independent Research Fellowship NE/T011920/1 and from NERC award NE/P011365/1. F.S. acknowledges NSF support.
Author information
Authors and Affiliations
Contributions
D.A.S. performed the analysis and wrote the paper with feedback from F.S. D.A.S. and F.S. jointly conceived the study and interpreted the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Geoscience thanks Vena Chu and Christoph Kittel for their contribution to the peer review of this work. Primary Handling Editor: James Super, in collaboration with the Nature Geoscience team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 An example subglacial discharge time series for Jakobshavn Isbrae in west Greenland.
(a) Hydrological drainage basin and (b) subglacial discharge.
Extended Data Fig. 2 An example ocean thermal forcing time series, for Helheim Glacier in south-east Greenland.
(a) Attempting to find ocean properties at 500 m depth. In this case there is a continuous path out of the fjord at 500 m depth that reaches shelf points in the ORAS5 reanalysis, but these shelf points do not have properties at 500 m depth because the bathymetry in the reanalysis is too shallow. Some points further offshore do have properties at 500 m depth, but these are not connected to the fjord at 500 m depth. (b) Attempting to find ocean properties at 350 m depth. In this case there are multiple shelf points in ORAS5 that are both connected to the calving front and have properties at 350 m depth (and this is the largest depth for which this is the case). We choose the closest point (blue diamond) to sample ocean properties for Helheim Glacier. The equivalent positions for CHORE_RL, EN.4.2.1 and ASTE_R1 are shown as the other coloured diamonds. (c) The resulting monthly thermal forcing time series for Helheim Glacier in each product, and the mean values that are finally used in this study.
Extended Data Fig. 3 Calibration of the summer submarine melt rate parameterisation using buoyant plume theory.
(a) Under variation in subglacial discharge, (b) variation in ocean thermal forcing and (c) variation in grounding line depth. In each panel, the markers are the full plume theory solution, while the lines are the fitted parameterisation shown in panel d. In panels (a)-(c) we hold two variables constant and vary the third. In panel (d) all three variables are varied.
Extended Data Fig. 4 An illustration of results from the glacier model.
(a) Submarine melt rate time series obtained from the melt rate parameterisation and data sources. The other subplots show simulated (b) absolute ice discharge, (c) absolute terminus position, (d) absolute sea level contribution, (e) normalised ice discharge, (f) normalised retreat and (g) normalised sea level contribution. (b) and (c) show both seasonal and smoothed time series. (b) and (d) assume a glacier width of 5 km so that the results may be expressed in terms of mass, but the normalised time series used in the main article are independent of the choice of width. All plots show the three submarine melt scenarios: atmosphere varies, ocean varies and both vary.
Extended Data Fig. 5 Relationship between key quantities and grounding line depth.
All values are 1979-2018 averages as in Fig. 2 of the main article. (a) subglacial discharge (note logarithmic scale), (b) thermal forcing and (c) submarine melt rate. All plots are coloured by ice sheet sector as defined in Fig. 2 of the main article, and trends lines are shown where the relationship between the quantity and the grounding line depth is significant at the 5% level. There is therefore a significant relationship between subglacial discharge and grounding line depth for central-west and north-west Greenland. There are significant relationships between thermal forcing and grounding line depth, and submarine melt rate and grounding line depth, for all regions.
Extended Data Fig. 8 Modeled regional retreat as in Fig. 4 of the main article, but with observations from48 shown in yellow.
When comparing model and observation, note that due to the normalisation, the model and observations automatically agree at the start and end of the time series. These plots do not, therefore, indicate that the model captures the magnitude of retreat, but they do show some ability to capture the timing of retreat.
Extended Data Fig. 9 Simulated importance of atmospheric and oceanic variability to glacier ice discharge.
Figure is the equivalent of Fig. 4 of the main article, but showing normalised ice discharge instead of retreat and dynamic sea level contribution.
Extended Data Fig. 10 A version of Fig. 4 of the main article showing sensitivity to the ocean reanalysis product used.
All lines show the ensemble median of the glacier simulations forced by the indicated ocean reanalysis product. As in Fig. 4, blue lines show simulations in which only the atmosphere is allowed to vary while red lines show simulations where only the ocean is allowed to vary. All results are plotted relative to the retreat or sea level in 2018 in simulations where both atmosphere and ocean vary. Note that ASTE is not shown as it begins in 2002 and so is difficult to plot on a figure showing retreat or sea level change since 1979.
Supplementary information
Supplementary Information
Supplementary description of methods, model and analysis.
Extended data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Slater, D.A., Straneo, F. Submarine melting of glaciers in Greenland amplified by atmospheric warming. Nat. Geosci. 15, 794–799 (2022). https://doi.org/10.1038/s41561-022-01035-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41561-022-01035-9
This article is cited by
-
Atlantic Water warming increases melt below Northeast Greenland’s last floating ice tongue
Nature Communications (2024)
-
Heterogeneous impacts of ocean thermal forcing on ice discharge from Greenland's peripheral tidewater glaciers over 2000–2021
Scientific Reports (2024)
-
Extreme summer temperature anomalies over Greenland largely result from clear-sky radiation and circulation anomalies
Communications Earth & Environment (2024)
-
Sediment discharge from Greenland’s marine-terminating glaciers is linked with surface melt
Nature Communications (2024)
-
Abrupt increase in Greenland melt enhanced by atmospheric wave changes
Climate Dynamics (2024)