Main

The Earth’s lithosphere is defined by its mechanically rigid behaviour in contrast to the relatively weak underlying asthenosphere. This rheological stratification, which ultimately allowed for the emergence of plate tectonics, results primarily from the thermal gradient across the crust and upper mantle and the temperature-dependent activation of dislocation- and diffusion-related crystal–plastic creep of rocks and minerals1,2,3,4. Scaling of such experimentally derived creep laws to natural strain rates allows us to estimate viscosities and strength of the lithosphere (Extended Data Fig. 1). Geophysical constraints on the elastic thickness of the continental lithosphere, which is a proxy for its strength, led to contrasting views on the strength of the uppermost mantle, with it being either strong and best represented by dry dislocation creep of olivine5 or weak according to a wet olivine rheology6,7.

Whether deformation within the upper mantle is dominated by dislocation creep or diffusion creep is still a matter of debate. The observation of crystallographic preferred orientation in mantle xenoliths8 and evidence for strong seismic anisotropy9 has long been interpreted as an indicator for dislocation creep as the dominant deformation mechanism10. However, there is reported evidence that crystallographic preferred orientation, and therefore seismic anisotropy, may also develop as a result of diffusion creep of fine-grained olivine-rich aggregates11. In contrast to dislocation creep, the relationship between stress and strain rate for diffusion creep is dependent on grain size, which is a crucial parameter when considering the dominant deformation mechanism in the upper mantle1,3,12. A transition from dislocation to diffusion creep at depths greater than ~250 km was proposed by Hirth and Kohlstedt1 on the basis of theoretical estimates that olivine grain size in the upper mantle is on the order of 10 mm13. Numerical experiments of mantle convection have since implemented a composite diffusion–dislocation creep rheology and constant mantle grain size, which may result in dramatic convective instability and thermal erosion of the lithosphere14. However, the assumption of a constant upper-mantle grain size is an oversimplification that appears contradictory to several observational and experimental datasets. Experimental data on wave speed and attenuation of olivine, for example, fit best with a seismological model that implies an increase in grain size from ~1 mm to ~5 cm between depths of 100 and 200 km15. Furthermore, natural samples of exhumed lithospheric mantle rocks show a large variety of grain sizes ranging from tens to hundreds of microns in olivine mylonites and tectonites to the centimetre scale in weakly deformed or annealed xenoliths16,17,18.

Plate tectonics requires mechanical weakening and prolonged strain localization along lithospheric shear zones at the plate boundaries19,20. Several studies suggest that grain-size reduction and the consequent activation of diffusion creep is a viable process to initiate localization of deformation in the lithosphere21,22,23,24,25, perhaps complementary to other potential weakening mechanisms such as shear heating26, reaction-induced weakening27 or the presence of pre-existing weak zones or viscous anisotropy28. For example, Bercovici and Ricard29,30 demonstrated that dynamic grain damage and phase mixing may explain fast (<1 Myr) weakening and localization of shear zones because Zener pinning severely inhibits the process of grain growth. By contrast, long-term grain-size-dependent weakening in the absence of grain pinning has been considered unlikely31 due to fast grain-growth laws for olivine32. Unfortunately, most models that investigate grain-size-related weakening describe one-dimensional parameterizations that lack the necessary dynamic context to better understand complex tectonic systems21,33,34. Furthermore, recent studies suggest that the coupling of grain size and thermo-mechanical systems has important effects on the dynamics of mantle convection35, the initiation of transfer faults25 and the segmentation of subducting slabs36.

In this Article, we present a two-dimensional thermo-mechanical numerical model with a composite diffusion–dislocation creep flow law coupled to a self-consistent grain-size-evolution model based on the palaeowattmeter37. Such a model allows us to estimate apparent grain-size distribution and the dominant deformation mechanism within the upper mantle and to investigate the importance of grain-size evolution for strain localization in the lithosphere during continental rifting. The two-dimensional approach furthermore allows for the evaluation of complex thermal and geometric feedback effects related to upper-mantle dynamics. We test the influence of hydrogen concentration in the mantle, which affects both its viscosity and rate of grain growth. Furthermore, the effect of localized grain-size-dependent weakening on the long-term strength and elastic thickness of continental lithosphere is investigated and compared with pure dislocation-creep experiments.

Modelling grain-size evolution in the upper mantle

We apply a finite-difference thermo-mechanical numerical model of the upper mantle and crust with a Eulerian domain of 1,000 × 670 km that undergoes horizontal divergence at a constant total rate of 1 cm yr–1 (Extended Data Fig. 2). Additional experiments were run with divergence rates of 4 and 8 cm yr–1 for comparison. The model employs a visco-elasto-plastic rheology where the viscous strain rate is composed of both dislocation and diffusion creep for a constant hydrogen concentration1 and stresses are capped depending on the Drucker–Prager yield criterion (Extended Data Tables 1–3 and Methods). Although grain boundary sliding (GBS) may be important in olivine at dry conditions38, it is expected to have a minor effect in wet experiments1, requiring either high stresses (>1 GPa) or high temperatures (>1,500 °C) for grain sizes of 1–10 mm (ref. 39). Nevertheless, we conducted additional experiments including a wet GBS flow law39 to test its effect on the mechanics of the upper mantle. The applied hydrogen concentrations in the mantle are COH = 50, 175, 600 and 2,500 H atoms per 106 Si atoms (H/106 Si), which cover the range of estimated values obtained from experimental studies40,41, and measured values from mid-ocean ridge basalts42, and peridotite xenoliths43 (Methods). Olivine grain size is calculated on the basis of the palaeo-wattmeter37, which introduces a grain-size-evolution rate composed of independent growth and reduction terms (Extended Data Table 4 and Methods). Grain-size reduction occurs through the process of dynamic recrystallization during dislocation creep, whereas grain growth controls the grain size during diffusion creep44. Therefore, only dislocation creep is responsible for grain-size reduction. On the basis of grain sizes from experimentally deformed olivine aggregates, the fraction of work that goes into grain-size reduction during dynamic recrystallization is estimated to be λ = 0.01 (Extended Data Fig. 3a), which is in agreement with recent estimates for olivine45. Additional experiments were conducted with λ = 0.003, 0.04 and 0.1 for comparison. The implemented grain-growth parameters derive from experiments on natural olivine aggregates with in situ hydrogen concentrations46 that predict substantially slower grain growth than previous constraints from experiments on water-saturated, synthetic olivine32 (Extended Data Fig. 3b). Grain sizes within the lithosphere are driven mainly by the reduction term due to lower temperatures and higher deviatoric stresses (Extended Data Fig. 3c). However, initial grain sizes in the lower part of the model domain rapidly adjust to a steady-state grain size due to high temperatures and thus fast growth rates (Extended Data Fig. 3d).,

Rheological implications and the formation of shear zones

Composite diffusion–dislocation-creep numerical experiments were conducted with various constant hydrogen concentrations in the mantle (COH = 50, 175, 600 and 2,500 H/106 Si) that affect both viscous creep and grain growth. Mantle viscosities of the reference model (COH = 600 H/106 Si) show values of 1019–1021 Pa s for the asthenosphere after 5 Myr of divergence (Fig. 1a). At 10 Myr, lithospheric thinning and related temperature increase below the rifted region lead to viscosities as low as 5 × 1017 Pa s, relatively fast velocities and gravitationally induced lithospheric dripping. After 15 and 20 Myr of divergence, asthenospheric viscosities remain within 1018–1021 Pa s, with lower values where fast velocities occur due to thermally and gravitationally induced lithospheric erosion (Fig. 1a). Away from the rift, the lithosphere remains intact and strong. Additional experiments including GBS deformation mechanism39 with hydrogen concentrations of COH = 50 H/106 Si indicate a negligible and for COH = 600 H/106 Si a minor (<1% of total strain rate) contribution of GBS to upper-mantle dynamics (Extended Data Fig. 4).

Fig. 1: Temporal evolution of the experiment with COH = 600 H/106 Si.
figure 1

a, Viscosity of upper mantle and marker composition of crust. White lines denote isotherms up to 1,300 °C. b, Deformation mechanism in the uppermost mantle and composition of crust. Red, diffusion creep; white, dislocation creep; blue contours indicate grain size; grey and yellow colours, continental crust marker composition; green, oceanic crust marker composition; x, width; y, depth.

Full size image

Illustrations of the dominant deformation mechanism (dislocation versus diffusion creep) and contours of grain size in the mantle demonstrate that localization of stress in the centre of the model domain leads to grain-size reduction and the activation of diffusion creep along large-scale lithospheric shear zones (Fig. 1b). The large shear zones retain relatively small grain sizes and remain dominated by diffusion creep even after 15 to 20 Myr of divergence, when a mid-ocean spreading centre is established, consuming most of the extensional velocity. This general observation is also valid if the fraction of work that goes into grain-size reduction is varied to λ = 0.004, 0.03 and 0.1, with larger λ values resulting in smaller grain sizes and a stronger impact of diffusion creep within the mantle lithosphere (Extended Data Fig. 5a–c). In contrast to the grain-growth law for natural damp olivine aggregates, the implementation of much faster grain-growth law from water-saturated synthetic olivine32 results in grain sizes responsible for dislocation creep dominating across the entire upper mantle and the lack of grain-size-induced weakening (Extended Data Fig. 5d). This result has previously led to the suggestion that phase mixing and grain boundary pinning is the primary driver for strain localization in mantle shear zones29. However, our results demonstrate that even in the absence of phase mixing, grain growth is sluggish enough to permit sustained localization through the persistence of diffusion creep after initial dynamic recrystallization. This result is consistent with observations from nature that many mantle shear zones also localize in olivine-dominated (for example, non-phase-mixed) peridotites such as dunites18,47.

For experiments with the recent grain-growth law and a λ = 0.01, grain sizes vary spatially throughout the model domain; furthermore, their values are strongly sensitive to implemented mantle hydrogen concentration. Vertical grain-size profiles along the side of the domain (at 5 Myr), away from the extensional zone, show values of 0.3–3.0 mm at the Moho (depending on COH) that increase to 6–15 cm at the lithosphere–asthenosphere boundary (LAB) and decrease to 3–10 cm at the base of the olivine-rich mantle at 410 km depth (Fig. 2a). Grain sizes within localizing shear zones in the uppermost lithosphere at 40 km depth (y = 50 km) show a rapid initial decrease to 60–250 μm (Fig. 2b). Depending on the hydrogen concentration in the mantle, they are able to recover after ~15 Myr (COH = 2,500 H/106 Si) or ~20 Myr (COH = 600 H/106 Si). Lower hydrogen concentration hampers substantial grain growth within previously active shear zones before 40 Myr. Average upper-mantle grain sizes below 300 km depth establish within ~2 Myr and range between 3 and 12 cm (Fig. 2c). Further undulations in average mantle grain size result from the downwelling of small-grain-size lithospheric driplets.

Fig. 2: Grain sizes in the mantle at variable water content.
figure 2

a, Vertical profile at x = 990 km after 5 Myr. See location in Fig. 1a. b, Temporal evolution of grain size within lithospheric shear zones at y = 50 km. c, Temporal evolution of grain size between 200 and 410 km depth.

Full size image

Figure 3 shows the portions of accumulated finite viscous strain within the mantle accommodated by diffusion and dislocation creep after 20 Myr of divergence. Dislocation creep is the dominant deformation mechanism in large parts of the upper mantle, independent of hydrogen concentration. Diffusion creep dominates within lithospheric shear zones that form in the early stages of rifting (Fig. 1b) and assist in lithospheric dripping (Fig. 3b–d). The continental lithospheric thickness defined by its viscosity varies between 90 and 150 km, depending on hydrogen concentration (Fig. 3).

Fig. 3: Percentage of finite strain accumulation in a lithospheric shear zone.
figure 3

Strain due to diffusion creep (blue) or dislocation creep (white) after 20 Myr of divergence. Red, contour of η = 1021.5 Pa s indicating thickness of the elastic lithosphere. a, COH = 50 H/106 Si. b, COH = 175 H/106 Si. c, COH = 600 H/106 Si. d, COH = 2,500 H/106 Si.

Full size image

Effects of grain size on lithospheric strength

The importance of a self-consistent grain-size distribution for upper-mantle dynamics becomes evident when comparing our results with numerical experiments with pure dislocation creep of olivine or composite diffusion–dislocation creep with a constant grain size throughout the entire upper mantle. Experiments with dry dislocation creep result in a thicker elastic lithosphere and increased viscosities (Extended Data Fig. 6a). Experiments with composite diffusion–dislocation creep and small constant grain size (1 mm) result in a lithosphere thinned by convective erosion (<90 km) driven by low asthenosphere viscosities of <1018 Pa s (Extended Data Fig. 6b). For constant grain sizes larger than 1 cm, dislocation creep becomes the main deformation mechanism throughout the entire upper mantle14. These numerical experiments fail to match the effective elastic lithospheric thicknesses necessary to sustain orogens5, while brittle deformation in the lithosphere remains absent7. However, our implementation of a self-consistent grain-size evolution is able to resolve this obstacle. Observed lithospheric thicknesses vary between 90 and 150 km (Fig. 3), while localization of deformation in the mantle lithosphere rapidly leads to grain-size reduction, diffusion-creep activation and related stress drop below the frictional yield, omitting failure. The diffusion-creep-related stress drop furthermore reduces and replaces the importance of (work-related) shear heating along lithospheric shear zones26,48.

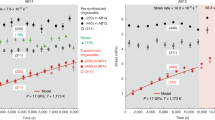
The temporal evolution of the vertically integrated strength illustrates that experiments with composite diffusion–dislocation creep coupled to a self-consistent grain-size evolution show a decrease of boundary forces below 5 TN m–1 within 1–2 Myr, while pure dislocation-creep experiments remain above 10 TN m–1 for at least ~15 Myr (Fig. 4a). Typical forces along plate boundaries are on the order of 1–5 TN m–1 (refs. 49,50), which is sufficient to initiate continental rifting if the grain size is small enough and diffusion creep dominates deformation23. Vertical strength profiles indicate that most of the strength of coupled experiments remains within the crust, with maximal values of ~200 MPa, while pure dislocation-creep experiments exhibit at least 10 km of brittle–plastic mantle lithosphere with differential stresses up to ~600–700 MPa (Fig. 4b). Differential stresses of ~200 MPa close to the Moho in composite diffusion–dislocation-creep experiments stand in contrast to significantly lower strength along a lithospheric shear zone after 5 Myr (Fig. 4c). There, values of 1–10 MPa are defined by grain sizes as small as 100 μm and diffusion creep as the consequent deformation mechanism, efficiently weakening the entire lithospheric rift system.

Fig. 4: Strength of the lithosphere.
figure 4

a, Temporal evolution of the laterally averaged integrated strength (boundary force) of pure dislocation and grain-size-dependent composite diffusion–dislocation-creep experiments. b, Laterally (x = 990–1,000 km) averaged lithospheric strength profiles after 5 Myr. For colour code, see a. c, Strength and grain-size profile along lithospheric shear zone at 5 Myr. Location of profile indicated in Fig. 1b.

Full size image

Hydrogen concentration in the upper mantle has important implications for the relationships between viscous flow and seismic anisotropy41, hydrous melting51 and the distribution of geochemical reservoirs52. The strength of olivine in the presence of water is significantly reduced53,54, as expressed in the flow law we apply1. Furthermore, increased hydrogen concentration results in faster olivine grain growth46. The combined increase in grain-growth rate and decrease in flow stress associated with higher hydrogen concentrations in our experiments leads to lower asthenospheric viscosity and increased thermal erosion of the lithosphere driven by diffusion creep (Fig. 3).

The numerically predicted olivine grain size in the upper lithosphere away from shear zones (0.5–10 mm; Fig. 2a) is in agreement with naturally measured values from exhumed xenoliths16,55,56. Furthermore, recrystallized grain sizes of 10–100 μm from localized lithospheric shear zones57,58,59 match the grain sizes established in the diffusion-creep-dominated numerical shear zones for hydrogen concentrations >175 H/106 Si (Fig. 2b). There are only a few constraints on grain size in the lower part of the upper mantle. However, Faul and Jackson15 suggested that the seismic signature of the upper-mantle low-velocity zone may be explained with a grain size of 5 cm together with the presence of fluids, which is consistent with our numerical results (Fig. 2a,b).

Implications for continental margin architecture

Numerical experiments with a self-consistent grain-size-evolution model result in reduced grain sizes and the consequent activation of diffusion creep below continental rift zones. The long-term low viscosity of such lithospheric shear zones leads to mechanical decoupling along the Moho and allows for stretching of the continental crust and the formation of a hyper-extended margin, where the continental crust is <10 km thick horizontally extended over >100 km with a lack of high-angle faulting60, forming continental slivers and extensional allochthons61 (Fig. 1b). Previous studies demonstrated that strain-dependent rheologies (either brittle or viscous strain weakening) of continental crust and lithospheric mantle play a crucial role in the formation of asymmetric rifting and hyper-extended margins62,63. In fact, numerical experiments with a pure dislocation-creep mantle flow and without a grain-size-dependent weakening consistently produce symmetric and localized rifts (Extended Data Fig. 6a). This is also the case for experiments with a constant grain size of 1 mm due to the strong, dislocation-creep-dominated uppermost mantle lithosphere (Extended Data Fig. 6b).

The formation of diffusion-creep-dominating mantle shear zones is also observed when increasing the divergence velocity of rifting experiments to a total of 4 and 8 cm yr–1 (Extended Data Fig. 6c,d). However, faster extension leads to increased rifting symmetry, with smaller grain sizes in the mantle lithosphere. The impact of weak rheologies and plate velocities on rift architecture is not novel62,63,64. However, in contrast to previous studies, we present a self-consistent fully coupled physical implementation supported by observed variance of grain size in mantle rocks that is responsible for crust–mantle mechanical decoupling necessary to form hyper-extended margins.

In summary, presented numerical results are able to reproduce naturally observed distributions of olivine grain size, which indicate that dislocation creep is the dominant deformation mechanism in the upper mantle except along lithospheric shear zones, where diffusion creep is activated as a result of grain-size reduction by earlier dislocation creep at high stress. This intrinsic weakness of such shear zones reduces the necessary boundary force to initiate continental break-up and accelerates related rifting events. A typical feature of our experiments including grain-size evolution is the development of hyper-extended margin architectures, enabled by mechanical decoupling along diffusion-creep-dominated weaknesses below the extending continental crust.

Methods

Numerical experiments were conducted with a finite-difference thermo-mechanical numerical code with a fully staggered Eulerian grid and a Lagrangian particle field based on the marker-in-cell technique65,66,67. The mechanical implementation employs a visco-elasto-plastic rheology, and governing equations are discretized on the non-deformable Eulerian grid and solved with MATLAB’s backslash direct solver for the two velocity components and dynamic pressure. Temperature is solved separately on the Eulerian pressure nodes with MATLAB’s backslash direct solver. Material properties are interpolated on freely moving Lagrangian markers that advect through the fixed Eulerian grid according to a fourth-order Runge–Kutta derived velocity field.

Governing equations

The mechanical model implements the equations for conservation of mass (incompressible)

$$\frac{{\partial u_i}}{{\partial x_i}} = 0$$
(1)

and conservation of momentum (Stokes equation)

$$\frac{{ - \partial P}}{{\partial x_i}} + \frac{{\partial \tau _{ij}}}{{\partial x_j}} = \rho g_i.$$
(2)

where P is mean stress, ui is velocities, xi is spatial coordinates, τij is deviatoric stress tensor, ρ is density and gi is the gravitational acceleration.

Temperature is implemented by the energy equation

$$\rho C_P\left( {\frac{{DT}}{{Dt}}} \right) = k\frac{{\partial ^2T}}{{\partial x_i^2}} + H_{\mathrm{a}} + H_{\mathrm{r}} + H_{\mathrm{s}}.$$
(3)

where T is temperature, t is is time, CP is isobaric heat capacity and k is thermal conductivity coefficient. Additional heat sources include adiabatic heating (Ha), radioactive heating (Hr) and shear heating (Hs):

$$H_{\mathrm{a}} = \alpha T\left( {\frac{{DP}}{{Dt}}} \right)$$
(4)
$$H_{\mathrm{s}} = \xi \sigma _{ij}\dot \varepsilon _{ij}$$
(5)

where ξ is fraction of work adding to shear heating. Hr is implemented as a constant for each rock type. Density changes related to thermal expansion α and compressibility β are implemented following

$$\rho = \rho _{\mathrm{r}}\left[ 1 + \beta \left( {P - P_{\mathrm{r}}} \right)\right] \times \left[ 1 - \alpha \left( {T - T_{\mathrm{r}}} \right)\right]$$
(6)

where ρr is reference density, Pr is reference pressure (1 bar), Tr is reference temperature (273 K), α is thermal expansivity and β is compressibility.

Rheological model

The visco-elastic relation between stress and strain rate follows a Maxwell-type model composed of a viscous and an elastic strain rate part

$$\dot \varepsilon _{ij} = \frac{1}{2}\tau _{ij} + \frac{1}{{2G}}\frac{{D\tau _{ij}}}{{Dt}},$$
(7)

where G indicates the shear modulus and η the effective viscosity with lower and upper cut-offs of 1017 and 1025 Pa s, respectively. Elasticity is implemented by adapting the effective viscosity depending on the ‘computational’ time step and the stress history65,68,69. The objective co-rotational time derivative of visco-elastic stresses is discretized as a function after applying first-order finite difference

$$\frac{{D\tau _{ij}}}{{Dt}} = \frac{{\tau _{ij} - \tau _{ij}^{{\mathrm{old}}}}}{{\Delta t}}$$
(8)

with

$$\tau _{ij} = 2\dot \varepsilon _{ij}Z + \tau _{ij}^{{\mathrm{old}}}\left( {1 - Z} \right)$$
(9)

and the visco-elasticity factor

$$Z = \frac{{\Delta t\times\Delta G}}{{\eta + \Delta t\times\Delta G}}$$
(10)

with η as effective viscosity, which leads to the numerical visco-elastic viscosity

$$\eta _{{\mathrm{num}}} = \eta \times Z = \frac{{\eta \times \Delta t \times G}}{{\eta \ + \Delta t \times G}}$$
(11)

used to solve the set of equations.

The viscous strain rate is composed of both dislocation and diffusion creep following the general power law for a viscous implementation1:

$$\dot \varepsilon = A_D \times f{\mathrm{H}_{2}{\rm{O}}}^r \times \sigma ^n \times d^m \times {\mathrm{exp}}\left( { - \frac{{E + P \times V}}{{RT}}} \right),$$
(12)

where AD is pre-exponent, fH2O is water fugacity, r is water-fugacity exponent, σ is stress, n is stress exponent, d is grain size, m is grain-size exponent, E is activation energy, V is activation volume and R is gas constant (8.314 J K–1 mol–1).

Viscosities for dislocation creep ηdisl and diffusion creep ηdiff are calculated separately by reformulating the general viscous power law (equation (12)):

$$\eta _{{\mathrm{disl}},{\mathrm{diff}}} = 0.5 \times \frac{1}{{A_D\,f{\mathrm{H}_{2}{\rm{O}}}^r}} \times \sigma _{{\mathrm{II}}}^{(1 - n)} \times d^{ - m} \times {\mathrm{exp}}\left( {\frac{{E + PV}}{{RT}}} \right)$$
(13)

with

$$\sigma _{{\mathrm{II}}} = \sqrt {\frac{1}{2}\tau _{ij}^2} .$$
(14)

The composite viscosity resulting for the simultaneous occurrence of dislocation and diffusion creep follows

$$\eta _{\mathrm{v}} = \left( {\frac{1}{{\eta _{{\mathrm{disl}}}}} + \frac{1}{{\eta _{{\mathrm{diff}}}}}} \right)^{ - 1}$$
(15)

Extended Data Fig. 1 shows vertical viscosity (Extended Data Fig. 1a–c) and strength profiles (Extended Data Fig. 1d–f) for variable grain sizes, strain rates and hydrogen concentrations. Such an illustration helps interpret the dominating deformation mechanism in the uppermost mantle depending on the investigated variables.

Plastic failure occurs if the visco-elastic differential trial stresses exceed the yield stress (F > 0) according to the Drucker–Prager yield criterion with a flow potential resulting in a dilation angle of zero:

$$F = \sigma _{{\mathrm{II}}} - \sigma _y$$
(16)

where

$$\sigma _y = P \times \left( {1 - \lambda _{\mathrm{f}}} \right) \times \sin \varphi + C \times \cos \varphi$$
(17)

where C is cohesion, φ is friction angle and λf is fluid pressure ratio. Exceeded stresses are kept within the failure envelope by decreasing the plastic viscosity ηp to maintain those stresses

$$\eta _{\mathrm{p}} = \frac{{\sigma _y}}{{2\dot \varepsilon _{{\mathrm{II}}}}}$$
(18)

where

$$\dot \varepsilon _{{\mathrm{II}}} = \sqrt {\frac{1}{2}\dot \varepsilon _{ij}^2} .$$
(19)

The effective viscosity going into the viscous part of the Maxwell rheological model follows

$$\eta = \min \left( {\eta _{\mathrm{v}},\eta _{\mathrm{p}}} \right).$$
(20)

After interpolation of the Eulerian velocity field onto the Lagrangian markers, stress changes and plasticity are calculated on those. The updated effective viscosity is then interpolated back onto the Eulerian nodes and used to solve the system of equations. Time steps exhibit maximally ≤1,000 yr following a Courant number of 0.25.

Grain-size-evolution model

Grain size is calculated on the basis of the palaeo-wattmeter37, in contrast to grain-size pinning and damage in a two-phase medium. Grain size depends on independently acting growth and reduction terms29,36 (see ref. 33 for a comparison). Grain-size reduction rate is related to mechanical work executed by dislocation creep (\(\sigma \dot \varepsilon _{{\mathrm{disl}}}\)) and is described by

$$\dot{d} _{\mathrm{red}} = \frac{{{{{{\sigma }}}}\dot \varepsilon _{{\mathrm{disl}}}{{{{\lambda }}}}{{{{d}}}}^2}}{{{{{{c}}}}{{{{\gamma }}}}}},$$
(21)

where σ is stress, \({\dot \varepsilon _{\mathrm{disl}}}\) is dislocation-creep strain rate, c is a geometric constant (π for spheric grains), γ is the grain boundary energy (1.4 J m–2 for olivine70) and λ denotes the fraction of work that goes into grain-size reduction (λ = 1 – ξ), whereas the rest of the work goes into the shear heating term (Hs; see equation (5))71,72,73. Fitting experimentally derived olivine grain sizes versus expected grain size using the palaeo-wattmeter with the grain-growth law constrained by ref. 46 and others resulted in a λ of 0.01 (Extended Data Fig. 3a). The constrained fraction of work that adds to the grain-size reduction term is substantially smaller than previously applied fractions of λ = 0.1 (refs. 21,35,37). However, a recent study demonstrated that the energy partitioning factor λ of olivine ranges between 0.003 and 0.040 for a wide spectrum of pressure and temperature conditions45 (Extended Data Fig. 5).

Grain-growth rate follows a normal relationship given by

$$\dot{d} _{\mathrm{gr}} = {{{{K}}}}_{{{{{\mathrm{g}}}}}}{{{{f{\mathrm{H}}}}}}_2{{{{{\mathrm{O}}}}}}\exp \left( { - \frac{{{{{{E}}}}_{{{{{\mathrm{g}}}}}} + {{{{P}}}} \times {{{{V}}}}_{{{{{\mathrm{g}}}}}}}}{{{{{{RT}}}}}}} \right){{{{p}}}}^{ - 1}{{{{d}}}}^{1 - {{{{p}}}}},$$
(22)

where Kg is growth-rate constant, fH2O is water fugacity, Eg is activation energy, Vg is activation volume, P is pressure, T is temperature, R is gas constant, d is grain size and p is growth exponent. We applied experimentally derived olivine grain-growth parameters by ref. 46 and others that result in significantly slower grain growth than previous constraints32 (Extended Data Figs. 3b and 6). The new grain size dnew is calculated on the Lagrangian markers following

$${{{{d}}}}_{{{{{{\mathrm{new}}}}}}} = \left( {{{{\dot{d}}}}_{{{{{{\mathrm{gr}}}}}}} - {{{\dot{d}}}}_{{{{{{\mathrm{red}}}}}}}} \right) \times {{{{Dt}}}}$$
(23)

and then goes into the power-law creep calculation for diffusion creep (equation (13)).

Model set-up

The Eulerian model domain measures 1,000 × 670 km in x and y directions, respectively (Extended Data Fig. 2). The nodal resolution is 501 × 336 in x and y directions, which results in a cell size of 2 × 2 km. Rock type, rheological information and mechanical, thermal and grain-size material properties (Extended Data Tables 1–4) are stored on 25 Lagrangian markers per Eulerian cell. The initial marker distribution (Extended Data Fig. 3) describes, from top to bottom, (1) a 10-km-thick layer of low-viscosity sticky air, which allows for a quasi-stress-free surface (air–rock interface)74, (2) a 23-km-thick upper continental crust with quartzite rheology2,75, (3) a 10-km-thick lower continental crust with anorthite rheology4 and (4) 627 km of upper mantle with dry or wet olivine rheology1. Although no olivine occurs below 410 km depth (transition to wadsleyite, ringwoodite and majorite), olivine rheology is implemented here for the entire upper mantle for simplification and due to the lack of respective flow laws. A weak inclusion of 4 × 4 km of quartzite rheology is placed in the lower continental crust at x = 500 km to localize rifting at the centre of the model (Extended Data Fig. 2).

Fugacity in the upper continental crust is calculated after ref. 76. In the upper mantle, fugacity is implemented as constant hydrogen concentration obtained and constrained following the Paterson calibration77 with values of COH = 50, 175, 600 or 2,500 H/106 Si, covering the range of estimated values obtained from experimental studies40,41 as well as measurements from mid-ocean-ridge basalts42,78 and peridotite xenoliths43, which affects both viscosity (equation (13)) and grain growth (equation 22)). Elevated hydrogen concentrations in the upper mantle are introduced due to dehydration of subducting slabs or released from the mantle transition zone79.

The initial temperature distribution describes 0 °C within the sticky-air layer, a linear increase from 0 °C at the surface (y = 10 km) to 660 °C at the Moho (y = 43 km), and from there to 1,345 °C at the thermally induced LAB at 150 km depth (y = 160 km). Below the LAB, a static temperature increase of 0.5 °C km–1 is introduced. Such a temperature distribution is in agreement with the thermal structure of the lithosphere below continents80.

Oceanic crust with an anorthite–diopside (50/50) rheology81 is produced if mantle rock markers less than 8 km below the surface (air–rock interface) have a temperature of <400 °C.

Boundary conditions

Lateral boundaries prescribe a constant horizontal velocity of vx = –0.5 cm yr−1 on the left and vx = 0.5 cm yr−1 on the right side (Extended Data Fig. 1). In addition, experiments with a total horizontal divergence of 4 and 8 cm yr–1 were conducted (Extended Data Fig. 6c,d). Vertical velocities at lateral boundaries prescribe a free-slip condition (zero shear stress). Top and bottom boundaries exhibit vertical velocities to ensure conservation of area during divergence (Extended Data Fig. 1) and horizontal velocities prescribing free slip.

Initial grain-size distribution

Grain sizes in the crust remain constant at 1 mm. Initial grain size in the mantle of all experiments in the main figures logarithmically increases from 5 mm at the Moho to 10 cm at the LAB and 10 cm throughout the lower part of the mantle. Extended Data Fig. 3 shows the grain-size distribution within the uppermost 300 km after 10 Myr (Extended Data Fig. 3a) and the temporal evolution of average grain size between 200 and 410 km depth (Extended Data Fig. 3b) for different initial conditions. Grain sizes within the lithosphere are driven mainly by the reduction term due to lower temperatures. High temperatures and thus fast growth rates allow the lower part of the model domain to rapidly restore deformation-related reduced grain sizes. As a result, the initial grain size within the lower 300 km of the model is of little importance, while initial grain sizes should be large enough throughout the lithosphere not to be dependent on initial growth.

Surface-evolution model

The surface line (rock–air interface) undergoes simple syn-tectonic sedimentation and erosion mimicked by a linear diffusion scheme

$$\frac{{\partial h_s}}{{\partial t}} = \kappa \frac{{\partial ^2h_s}}{{\partial x_i^2}},$$
(24)

where h is surface elevation and κ is diffusion coefficient (10−6 m2 s–1). Syn-tectonic sediments have equal material and strength properties as the initial sediment sequence.