Abstract
Global climate is thought to be modulated by the supply of minerals to Earth’s surface. Whereas silicate weathering removes carbon dioxide (CO2) from the atmosphere, weathering of accessory carbonate and sulfide minerals is a geologically relevant source of CO2. Although these weathering pathways commonly operate side by side, we lack quantitative constraints on their co-variation across erosion rate gradients. Here we use stream-water chemistry across an erosion rate gradient of three orders of magnitude in shales and sandstones of southern Taiwan, and find that sulfide and carbonate weathering rates rise with increasing erosion, while silicate weathering rates remain steady. As a result, on timescales shorter than marine sulfide compensation (approximately 106–107 years), weathering in rapidly eroding terrain leads to net CO2 emission rates that are about twice as fast as CO2 sequestration rates in slow-eroding terrain. We propose that these weathering reactions are linked and that sulfuric acid generated from sulfide oxidation boosts carbonate solubility, whereas silicate weathering kinetics remain unaffected, possibly due to efficient buffering of the pH. We expect that these patterns are broadly applicable to many Cenozoic mountain ranges that expose marine metasediments.
Similar content being viewed by others
Main
Silicate weathering is a key component of Earth’s long-term carbon cycle. It neutralizes CO2 emissions from the crust and mantle by producing alkalinity, thereby driving precipitation of carbonates in the oceans1. Weathering rates are controlled by temperature, the availability of weathering fluids and the reactive mineral surface area2. They can be limited either by the supply of minerals (supply limit)3,4,5, by the kinetics of weathering reactions (kinetic limit)3,4 or by the availability of acidic fluids (equilibrium limit; see Table 1 for definitions)5. As a result, an intimate link emerges between chemical weathering, the supply of fresh rocks by physical erosion and climate4,6,7,8,9. The sensitivity of weathering to erosion rates underpins the hypothesis that major orogenic events can lead to increased silicate weathering rates, which decreases atmospheric CO2 concentrations and cools the planet7,10,11,12.
Most Cenozoic orogens do not exhume pure silicate rocks, but instead expose lithologies, such as shallow marine metasediments, that contain accessory carbonate and sulfide minerals. Recent studies found that weathering of these accessory minerals complicates the simple link between the supply of fresh rocks by erosion, enhanced weathering rates and drawdown of atmospheric CO2. Importantly, sulfuric acid that is produced during the oxidation of sulfide minerals, such as pyrite, can titrate alkalinity13,14. Therefore, silicate weathering by sulfuric acid does not contribute to CO2 drawdown, whereas carbonate weathering by sulfuric acid releases CO213,14. Because carbonate and sulfide minerals dissolve up to three orders of magnitude faster than silicates2,15,16, they frequently dominate weathering fluxes, even where they constitute only minor proportions of the exposed lithologies12,13,14,17,18. Moreover, sulfide weathering rates increase with erosion, and the consequent titration of alkalinity has been proposed to compensate for increases in silicate weathering rates during mountain building12,13,14,19.
Based on these studies, existing global carbon cycle models assume that the weathering rates of all mineral phases, including sulfides, carbonates and silicates, increase with erosion and proceed independently of each other1,9,10,20. However, where these weathering processes operate side by side, the acidity produced by sulfide oxidation may modulate silicate and carbonate weathering rates, with consequences for the carbon cycle13,14,21,22. Critically, we lack quantitative constraints on silicate, carbonate and sulfide weathering rates in parallel across extensive and continuous erosion rate gradients without accompanying variations in runoff, temperature and lithology. In existing compilations where erosion rate and runoff are correlated4,8,18, unravelling the impact of mineral supply on weathering rates is challenging, because runoff impacts weathering23,24. As a consequence, it remains unclear how weathering of accessory sulfide and carbonate minerals co-evolve across erosion rate gradients, and how the supply of fresh minerals during mountain building impacts the balance of CO2 emission and sequestration and, ultimately, Earth’s climate.
Here we present water chemistry data from streams in southern Taiwan that span an erosion rate gradient of nearly three orders of magnitude in a relatively homogeneous substrate with minimal variations in runoff. These data allow us, for the first time to our knowledge, to quantify the impact of erosion rates—independent of lithology and runoff—on the concomitant variation of carbonate, silicate and sulfide weathering and, thereby, on the sequestration and emission of CO2 from these weathering reactions.
Water chemistry in southern Taiwan
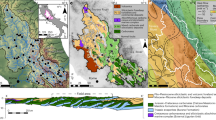
We present 103 water samples from 40 separate catchments that span a striking gradient of northward-increasing relief, channel steepness and erosion rates25,26,27 (Fig. 1). Erosion rate estimates from cosmogenic nuclide data are available for a subset of the sampled catchments26,27. These 10Be erosion rate data are well correlated with the normalized catchment-averaged steepness index (ksn), and we used a regression to predict the erosion rate for each sample from its catchment-averaged ksn estimate (Extended Data Fig. 1). Results show a northward increase of inferred erosion rates from <0.004 to >2 mm yr−1. In contrast to this erosion rate gradient of three orders of magnitude, average annual rainfall and inferred runoff vary by no more than a factor of three within the study area28,29. The bedrock in the sampled catchments is dominated by mildly metamorphosed calcareous argillites and shales of the Cenozoic slate belt30 (Fig. 1). In the northernmost part of the study area, these rocks unconformably overlie high-grade metapelites, whereas the southernmost tip of the island is characterized by alternations of sandstones and shales of the Mutan formation30. Minor carbonate is found as interstitial cement, clastic grains or in veins, in all formations of the study area, and pyrite occurs as a minor rock building mineral30 (Supplementary Text 1).
Map of the southern tip of Taiwan showing all sampling locations. Major lithological units and structures are modified after refs. 30,50. Symbols for water samples indicate dominant lithology outcropping in the catchment. Light grey lines mark the 40 unique catchments sampled here. Two rivers mentioned in the main text are marked.
For all samples, we measured concentrations of major dissolved cations, anions and silica. Across the erosion rate gradient, we find an increase in the concentrations of Ca2+ and SO42− ions (Fig. 2a), whereas Na+ and dissolved silica show constant concentrations at low erosion rates and a decrease at high erosion rates (Fig. 2b). The concentrations of Mg2+ and K+ do not change systematically (Fig. 2c). We used an inverse approach to estimate the cation concentrations contributed from silicates ([Cat]sil ; Fig. 2d), carbonates ([Cat]carb; Fig. 2e), hotsprings and cyclic sources (Extended Data Fig. 2), as well as the fraction of the total cation charge derived from carbonate weathering (fcarb; Fig. 2f). We further estimated the concentration of sulfates contributed from pyrite oxidation ([SO4]w; Fig. 2e), the fraction of weathering by sulfuric acid (fsulf; Fig. 2f) and the concentration of Ca2+ lost to secondary precipitation of carbonate (Fig. 2d). Inputs from evaporites and anthropogenic pollution are considered negligible (Methods).
a–e, Concentrations of calcium and sulfate (a), silica and sodium (b), magnesium and potassium (c), cations from carbonate weathering (d) and cations from silicate weathering and sulfate from sulfide oxidation (e). f, Fraction of cation charge contributed from carbonate weathering and fraction of cation charge balanced by sulfate. All results are plotted against the catchment-averaged steepness index (lower x axis) and inferred erosion rates (upper x axis). Symbols mark dominant lithology (see Fig. 1). Error bars are equivalent to a 95% confidence interval. Samples with anomalously high sulfate concentrations are marked as darker points.
Based on the inversion, weathering inputs dominate the solute load and contribute a median of ~88% (first quartile 74%, third quartile 95%) of the total cation budget, whereas the remaining solutes are related to cyclic and hotspring inputs. We find that silicate and carbonate cation concentrations are similar (fcarb ≈ 0.5) for erosion rates <0.1 mm yr−1 (Fig. 2f). At higher erosion rates, [Cat]carb increases five- to tenfold, whereas [Cat]sil remains constant or even declines, resulting in a dominance of carbonate weathering (fcarb = 0.8–1; Fig. 2d–f). In turn, sulfate concentrations from sulfuric acid weathering increase monotonically by more than 40-fold from <50 to >2,000 µmol l−1 as erosion increases (Fig. 2e). Consequently, fsulf increases from near 0% to about 50% from low to high erosion rates (Fig. 2f).
Silicate, carbonate and sulfide weathering
Using our new water chemistry data, we investigate the limits to weathering of sulfide, carbonate and silicate phases in parallel across a single erosion rate gradient. Because runoff is inferred to vary by less than two- to threefold across the erosion rate gradient28,29, we interpret the solute concentrations to be proportional to weathering rates (within a factor of two to three). The steady, 40-fold increase in concentrations of sulfates (Fig. 2e) suggests that pyrite weathering is limited by the supply of fresh minerals to the weathering zone (supply limit). Such supply limitation is consistent with previous studies14 and with the observed depletion of pyrite in the deepest parts of the weathering zone31,32. The supply of sulfuric acid by sulfide oxidation has been hypothesized to either increase both carbonate and silicate weathering rates14 or to boost only carbonate weathering13. Our observations suggest that carbonate weathering rates are closely associated with sulfuric acid addition, whereas silicate weathering rates are decoupled (Fig. 3a).
a, Co-variation of cation concentrations with sulfate. b, Predicted maximum pH in the weathering zone (pHeq) against catchment-averaged steepness index (lower x axis) and inferred erosion rates (upper x axis). c, Predicted pH for a carbonate-buffered solution after addition of sulfuric acid (\({\mathrm{pH}}_{{\rm{SO}}_4}\)) against the equilibrium pH. The solid line shows regression with 95% confidence bands; the dotted lines show initial pH before addition of sulfuric acid. Symbols mark dominant lithology (see Fig. 1). Error bars are equivalent to a 95% confidence interval. Samples with anomalously high sulfate concentrations are marked as darker points.
Carbonate weathering in Taiwan seems to be limited by the saturation of weathering fluids (equilibrium limit), based on several observations that include supersaturation of stream waters with respect to calcium carbonate (Extended Data Fig. 3), secondary carbonate precipitates around springs (see Fig. 2 in ref. 33) and the presence of detrital carbonate in streams. Yet, despite this equilibrium limit, [Cat]carb increases across the erosion rate gradient (Fig. 2d,f). This key observation implies that the solubility of carbonates must increase with erosion. A northward trend of cooling water temperatures from ~30 ± 5 to ~23 ± 4 °C can only account for a <1.7-fold increase in [Ca2+], much lower than the observed 5- to 10-fold increase. In contrast, acid addition can increase carbonate solubility by an order of magnitude per unit pH decrease (Supplementary Text 2). Hence, based on the close association of sulfate concentrations with [Cat]carb (Fig. 3a), we propose that northward-increasing acid availability is the main driver of the solubility increase. We estimate the pH at which the sampled supersaturated river waters would be at saturation with calcium carbonate (pHeq)—a maximum estimate of the pH in the subsurface (Fig. 3b). This inferred equilibrium pH of the weathering fluids generally decreases with increasing erosion rates, mirroring the pattern of [Cat]carb (Fig. 3b). We find that this observed trend in pHeq can be explained to a large extent by an estimate of \({\mathrm{pH}}_{{\mathrm{SO}}_4}\), which we define as the pH that results from the addition of sulfuric acid to a carbonate-buffered solution (Fig. 3c). The deviation from the 1:1 line between pHeq and \({\mathrm{pH}}_{{\mathrm{SO}}_4}\) implies that we either overestimate the loss of carbonates to secondary precipitation, or that the supply of another source of acidity, for example carbonic acid, also increases with erosion rates. In either case, carbonate weathering increases substantially with erosion and appears strongly coupled to sulfuric acid supply.
In contrast to carbonate weathering, cation concentrations from silicate weathering do not increase or may even decline at higher erosion rates (Fig. 2e). An equilibrium limit whereby silicates are saturated is unlikely, because, similar to carbonates, the decrease of the solution pH by at least one unit (Fig. 3b) is expected to increase the solubility of silicates by a factor of three to ten34. Hence, silicate weathering in the study area appears limited across almost the entire erosion rate gradient of three orders of magnitude wide by the slow kinetics of silica dissolution3,4. This interpretation implies that silicate weathering kinetics are constant or declining from south to north. Northward-decreasing temperatures may explain a slowing of weathering kinetics by a factor of ~1.5–2.5 (Supplementary Text 2). In addition, the potential two- to threefold increase in runoff could dilute major cations, although the dilution is probably less than a factor of two to three (see Supplementary Text 2). In contrast, silicate weathering kinetics can be strongly modulated by the solution pH and increase by up to an order of magnitude per unit of pH change, both with increasing acidity (at pH <5–6) and with increasing alkalinity (at pH >8–9)2,35. Such changes would more than compensate for the potential impact of temperatures or runoff. However, at circumneutral pH values of ~6–8 the dissolution rate of feldspars is at a minimum and insensitive to pH changes35. The observed invariance or even slight decline of silicate weathering kinetics despite a 40-fold increase in the supply of sulfuric acid (Fig. 2e) is, therefore, notable. The subsurface pH appears to be sufficiently buffered to within circumneutral values to prevent any substantial increase in silicate weathering kinetics by the addition of sulfuric acid. On the contrary, addition of sulfuric acid may even slightly decrease weathering rates by pushing the pH from alkaline (pH ~8.5) to circumneutral. Such buffering of the pH is consistent with subsurface pH values inferred from carbonate equilibria (Fig. 3b), and it provides a compelling explanation for the differential coupling of silicate and carbonate weathering to sulfide oxidation (Fig. 3a).
By observing the weathering of sulfide, silicate and carbonate across a single erosion rate gradient, we find that rock mass weathering does not have a universal limit. Rather, across a large range of erosion rates in the mountains of Taiwan, silicate weathering is kinetically limited, carbonate weathering is equilibrium limited and sulfide weathering is supply limited. Moreover, our data suggest that the supply of sulfuric acid does not increase weathering rates of both silicates and carbonates as previously hypothesized14, even though sulfuric acid probably contributes to weathering of both phases22. Instead, we propose that in metasediments with sufficient buffering capacity, the supply of sulfuric acid increases the equilibrium limit of carbonates, whereas buffering of weathering fluids at circumneutral pH prevents an increase in silicate weathering rates. The details of this coupling depend on the relative positions of weathering fronts and the distribution of mineral phases in the subsurface32, but the dominance of carbonate weathering, especially at high erosion rates (Fig. 2), implies that most sulfuric acid must be buffered by carbonates, as previously described for shale weathering36.
The observed trends continue across the lithologic boundary between the more sand-rich Mutan formation and the more shale-rich slate belt (Fig. 1). Lithology may cause a change in the trend between carbonate weathering rates and erosion rates (Fig. 2d), and local lithologic variations may lead to anomalously high sulfate concentrations of some samples. Nevertheless, our observations also hold when only catchments in the slate belt are considered (circles in all figures; spanning a ~200-fold range of estimated erosion rates). The similarity of samples collected under different hydrological conditions across two field seasons—a dry winter and a wet spring (Extended Data Fig. 4)—suggests that the broad patterns we observe hold across variations in discharge. Moreover, the chemistry of many streams is relatively insensitive to short-term variations in runoff24,37, and Taiwanese catchments typically show dilution by factors of less than five across discharge ranges of several orders of magnitude38,39. In apparent contrast to our findings, existing global compilations of river chemistry often find a positive link between silicate weathering fluxes (that is, the concentration multiplied by runoff) and erosion4,8. However, these positive correlations are frequently dominated by a strong co-variation of runoff and erosion rate. Because runoff can directly affect weathering rates23, this co-variation obscures the link between mineral supply and chemical weathering. Hence, a direct comparison between these data and our observations is difficult.
Impacts for Earth’s carbon cycle
Existing carbon cycle models typically assume that the reactivities of all mineral phases increase with rates of erosion and mineral supply, and evolve independently of each other1,9,10,20. As a consequence, decreasing atmospheric CO2 concentrations during the Cenozoic era have been linked to increased silicate weathering rates with uplift and erosion of the Alpine–Himalayan system7,10,11. In contrast, our data suggest that in the absence of a strong co-variation of mineral supply and runoff, increased erosion of marine siliciclastic sediment sequences may lead to a constant or even decreasing reactivity of silicate minerals, whereas carbonate and sulfide reaction rates increase (Fig. 2). We postulate that this co-variation of silicate, carbonate and sulfide weathering rates applies to erosion rate gradients in many active mountain ranges. Catchments in southern Taiwan are underlain by (meta)sedimentary rocks of an inverted passive margin sequence that is typical of rocks uplifted along active orogens. Moreover, solutes from carbonates and sulfides dominate total weathering budgets from freshly exposed metasediments in the Southern Alps of New Zealand18, the Himalaya17, the Rocky Mountains14, the Andes13 and even in slower-eroding continental interior settings such as northern Texas40. Finally, it is likely that sulfuric acid addition acts to increase silicate weathering rates only in rare cases, where acid production exceeds the buffering capacity of the sediment, for example in acid mine drainage41,42, or in headwater streams draining pure silicate lithologies43.
Relative changes in sulfide, silicate and carbonate weathering rates modulate the sequestration and release of CO2 on millennial to multi-million-year timescales13. In particular, the increase of sulfide weathering relative to silicate dissolution as erosion rates increase (Figs. 2 and 3) results in a clear shift from reactions that sequester CO2 to reactions that release CO2 (Fig. 4). In southern Taiwan, this shift occurs at erosion rates of ~0.3–1 mm yr−1 (Fig. 4). Importantly, CO2 release rates at erosion rates >1 mm yr−1 are substantially higher than CO2 sequestration rates at erosion rates of <0.1 mm yr−1 (Fig. 4). This contrast between CO2 release and sequestration may be even more pronounced where runoff increases in parallel with erosion rates4,8,44. As a result, the total CO2 release from mountain building may overwhelm CO2 drawdown from more slowly eroding landscapes, even if areas of high erosion rates do not cover the majority of exposed land area45.
Moles of CO2 emitted or sequestered per volume of water against catchment-averaged steepness index (lower x axis) and inferred erosion rates (upper x axis). Symbols mark dominant lithology (see Fig. 1). Error bars are equivalent to a 95% confidence interval. Samples with anomalously high sulfate concentrations are marked as darker points.
Ultimately, sulfuric acid generation by sulfide oxidation is balanced by marine sulfate reduction, although the timescale for achieving such a balance probably exceeds 106 years46. Thus, the shift from CO2 sequestration to CO2 emission with increasing erosion rates (Fig. 4) applies to timescales between those of carbonate compensation (~103–104 years) and pyrite neoformation in marine sediments (~106–107 years). These are the timescales of long-term climate change and mountain building. Even beyond the timescales of sulfide compensation in the ocean, the rate of CO2 sequestration from silicate weathering may be largely unaffected by mineral supply (Extended Data Fig. 5), because the concentration of solutes from silicate weathering does not increase across a large range of erosion rates (Fig. 2e). If our findings extend to metasediments globally, the Cenozoic decrease of atmospheric CO2 concentrations cannot be associated with an increased supply of minerals within inverted passive margins and must, instead, be linked to increased organic carbon burial47, increased relief and orographic precipitation23,44, alkalinity generation in floodplains48 or weathering of fertile igneous silicates49. Over the course of Earth history, the growing accumulation of carbonaceous shelf sediments on continental crust may thus have shifted orogenesis from a net sink of CO2 to a net source of CO2.
Methods
Notations and constants
We use the following notations (Extended Data Table 1): [i] is the concentration of ion i, υi is the valence of ion i, [i]eq = υi[i] is the charge equivalent concentration of ion i, γi is the activity coefficient of ion i and ai is the activity of ion i with ai = γi[i]. Subscripts carb, sil and sulf denote quantities calculated for the ions derived from carbonate, silicate and sulfide weathering, respectively, and the subscripts hs, cy, sc, m and wtot refer to contributions from hotsprings, cyclic sources, silicate and carbonate weathering, and to the total measured concentrations and the solutes from weathering reactions, respectively. We use the equilibrium constants and standard enthalpies as specified in Extended Data Table 2.
Water sampling and measurements
We collected 119 water samples across southern Taiwan for chemical analysis in 1 litre high-density polyethylene bottles from river banks with access to the main flow. The transition from colluvial to fluvial processes typically occurs around ~1 km2 of drainage area in Taiwanese mountain catchments51. Because a scaling of erosion rates and catchment-averaged steepness indices is only sensible within the fluvial regime, we limit our analysis to 104 samples with catchment areas of >2 km2. All samples were filtered the evening after sampling into a set of smaller high-density polyethylene bottles (for anion and cation measurements) using 0.22 µm Merck Express Plus membrane filters. We rinsed each bottle with filtered water before filling, and we acidified all bottles for cation analyses with concentrated ultrapure nitric acid (HNO3). We measured pH and temperature of the river in the field at the sample location using a WTW Multi 3430 multimeter and a WTW SensoLyt 900 pH probe. Electrical conductivity and dissolved oxygen content of the water were measured with a WTW TetraCon 925 and a WTW FDO 925 probe, respectively. After dilution with a caesium-spiked solution, cations (Ba2+, Ca2+, Fe2+, K+, Li+, Mg2+, Mn2+, Na+ and Sr2+) and dissolved silica were measured on a Varian 720 ICP-OES at the GFZ. Every ten samples, a quality control sample mixed at the GFZ was measured to monitor machine drift. All accepted runs had a drift of <5%. We measured external river water standards SLRS-5 or SLRS-6 and USGS-T187 and M212 for quality control. The measurements were calibrated using a set of 11 in-house standards, and any standards that did not fall within 10% of a linear fit through all standards were discarded. We used measurements only within the range of accepted standards, and estimated the uncertainty in the cation analysis from the maximum deviation of the calibration standards from the calibration line. We measured major anions (F−, Cl−, \({\mathrm{NO}}_3^ -\) and \({\mathrm{SO}}_4^{2 -}\)) on a Dionex ICS-1100 chromatograph using a six-point linear calibration and USGS-206 and USGS-212 standards for quality control. Uncertainty estimates were based on the standard deviation from three repeat measurements. Bicarbonate concentrations (\({\mathrm{HCO}}_3^ -\)) were estimated by charge balance, which assumes that the contribution of bicarbonate from organic sources is negligible (Supplementary Text 4). Uncertainties were propagated from the analytical uncertainties of the measured concentrations. All raw measurements are reported in Supplementary Data 1.
Erosion rate–k sn scaling
Catchment-averaged erosion rates are commonly well correlated with channel steepness, but the relationship has to be calibrated locally52. We used a regression between existing cosmogenic nuclide erosion rate data26,27 (Extended Data Fig. 1 and Supplementary Data 2) and the catchment-averaged steepness indices for all catchments with drainage areas of >2 km2 to predict catchment-averaged erosion rates for each of our water samples. First, we calculated mean steepness indices upstream of each cosmogenic nuclide sample and upstream of each water sample using TopoToolbox v2.253. Cosmogenic nuclide concentrations in southern Taiwan decrease northward, and concentrations in repeat samples collected in 2006, 2015 and 2016 generally agree26,27. We used a regression through the catchment-averaged normalized steepness and catchment-averaged erosion rates to predict, from the steepness index, a catchment-averaged erosion rate for each of the water samples collected in this study (Extended Data Fig. 1). Uncertainties in erosion rates were estimated from the confidence band of the regression. 10Be concentrations in samples collected in 2012 tend to be relatively lower and more scattered than during other years27. The decrease in 10Be concentrations of the 2012 samples was interpreted to result from extensive landsliding triggered by Typhoon Morakot in 200927, and we excluded these data from the analysis (blue points in Extended Data Fig. 1). Our water samples extend farther south than existing cosmogenic nuclide data. Therefore, all erosion rates <0.06 mm yr−1 were extrapolated from the regression (Supplementary Text 4).
Unmixing major contributions to the cation solute budget
We consider carbonates, silicates, cyclic water and hotsprings as major contributors to the cation budget (see endmembers in Extended Data Table 3, Supplementary Text 3 and Supplementary Data 3). No evaporite deposits have been reported in Taiwan30,54, and stream waters were collected upstream of major anthropogenically managed areas. In our analysis, we considered only the major cations Ca2+, Mg2+, K+ and Na+. The concentrations of cations derived from carbonate weathering, [Cat]carb, silicate weathering, [Cat]sil, the sum of silicate and carbonate weathering [Cat]wtot, cyclic contributions [Cat]cy and hotsprings [Cat]hs are:
We define corresponding charge equivalent concentrations, [Cat]eq, as:
The fraction of cation charge related to carbonate weathering, fcarb, and the fraction of cation charge balanced by sulfate, fsulf, are defined as:
We used an inverse approach to estimate the contribution of carbonate and silicate minerals to the dissolved solids. Following previous authors4,8,33,37,55, this estimate was based on modelling the relative concentrations of three major soluble cations, Na+, Ca2+ and Mg2+, as a mix of a silicate and a carbonate endmember (Extended Data Table 3). In addition, here we include the concentration of Cl−, to allow correction of the cyclic and hotspring contribution (Extended Data Table 3). Based on these endmembers, we solved the following equations using the linear least squares solver lsqlin in MATLAB:
under the conditions that:
and
where αCa,sil, αCa,carb, αCa,cy and αCa,hs are the fractions of calcium sourced from silicate weathering, carbonate weathering, cyclic input and hotspring input, respectively. Following previous authors37, we estimated sets of ‘best fit’ endmembers for each sample with 10,000 Monte Carlo runs. In each run, we randomly picked each endmember from normal distributions defined by the mean and the standard deviation of the local endmember estimates (Extended Data Table 3). For each sample, we then obtained an individual endmember estimate from the mean and standard deviation of all Monte Carlo runs that were weighted by the inverse chi-squared misfit between model and data of each run (Extended Data Fig. 6). One sample with an anomalously high ratio of \(\left[ {\frac{{\mathrm{Mg}}^{2 + }}{{\mathrm{Ca}}^{2 +}}} \right]\) was discarded from the inversion because it does not fall within the bounds of the silicate–carbonate–hotspring–cyclic endmember (Supplementary Fig. 2a).
Estimate of sulfuric acid contribution to weathering
The contribution of weathering by sulfuric acid was estimated from the total sulfate concentrations corrected for cyclic and hotspring inputs:
with
This calculation assumes negligible anthropogenic and evaporite inputs of sulfate to Taiwanese rivers and an absence of major sulfate sinks (Supplementary Text 4).
Corrections for secondary precipitation of calcite
Supersaturation of almost all sampled waters (Extended Data Fig. 3) and the presence of calcium carbonate precipitates near springs in the field (see Fig. 2 in ref. 33) attest to the importance of secondary calcite precipitation in the studied catchments. Supersaturation can occur where subsurface waters equilibrate at a high partial pressure of CO2 (that is, at a low pH) in soils and then degas CO2 in contact with the atmosphere. Degassing leads to secondary precipitation of CaCO3, but where secondary precipitation is incomplete, waters remain supersaturated. The enrichment of waters in Sr2+ relative to Ca2+ and Na+ can be used as an indicator for secondary precipitation of calcite33,56. Assuming that all measured Sr is contributed from chemical weathering, solutes from a mixed silicate and carbonate source that have not experienced re-precipitation of calcite should fall on a mixing line between a pure calcite endmember at \(\left[ {\frac{{\mathrm{Na}}^ + }{{\mathrm{Ca}}^{2 +}}} \right]\) close to zero and 1,000 × \(\left[ {\frac{{\mathrm{Sr}}^{2 + }}{{\mathrm{Ca}}^{2 +}}} \right]\) = 1 − 2, and a silicate endmember with both a higher \(\left[ {\frac{{\mathrm{Na}}^ + }{{\mathrm{Ca}}^{2 +}}} \right]\) and a higher \(\left[ {\frac{{\mathrm{Sr}}^{2 +}}{{\mathrm{Ca}}^{2 +}}} \right]\) ratio33. We assumed that the published elemental analyses of suspended sediments sampled in the Chenyoulan River33 (Supplementary Data 4) approximate the endmember mixing line between silicates and carbonates, and we found the best fit line through these data that is described by:
where a and b are the parameter of the linear fit (Extended Data Fig. 7). With precipitation of calcium, the Sr/Ca ratio increases according to:
where subscripts 0 and f denote the initial and final concentrations respectively, kd is the partition coefficient for Sr into abiotic calcite, and \(\beta = \frac{{\left[ {\rm{Ca}}^{2 + } \right]_{\rm{f}}}}{{\left[ {\rm{Ca}}^{2 + } \right]_0}}\) is the fraction of original calcite remaining in the water56. The partition coefficient has been shown to vary with precipitation rates and temperature between ~0.02 and 0.2 (refs. 57,58,59). The influence of this value is relatively small (Supplementary Text 4), so we follow refs. 33,56 and use a value of kd = 0.05. Moreover, we neglect incorporation of Mg into calcite, because Mg incorporation into calcite at concentrations of \(\left[ {\frac{{\rm{Mg}}^{2 + }}{{\rm{Ca}}^{2 + }}} \right] < 1\) (Extended Data Fig. 6) is expected to be <5%60,61. To estimate β (and thereby [Ca2+]0) we note that:
and because the concentration of sodium is unchanged:
From Eqs. (11) and (14) and the definition of β, we get:
Now, we have two estimates for \(\frac{{\left[{\mathrm{Sr}}^{2 + } \right]_0}}{{\left[{\mathrm{Ca}}^{2 + } \right]_0}}\) from equations (13) and (15), and we minimized the following equation numerically:
Uncertainties in the fraction of original calcite remaining in the water, β, were estimated from uncertainties in the regression parameters and the measured concentrations using a Monte Carlo routine. To this end, we repeated the minimization 10,000 times, randomly picking (1) the regression parameters from a bivariate normal distribution defined by the coefficients and variance–covariance matrix of the regression, and (2) [Sr2+], [Ca2+] and [Na+] from the normal distribution defined by the measurement and uncertainty. We then estimated the uncertainty of β from the standard deviation of β from all Monte Carlo runs. The final uncertainty in the corrected calcium concentrations was estimated from this standard deviation and the analytical uncertainty of the original calcium measurement.
CO2 budget from weathering reactions
We estimated the impact of erosion rates and the associated weathering patterns measured in Taiwan on the emission or drawdown of CO2 by considering the balance of alkalinity and dissolved inorganic carbon produced by weathering (see Table A.1 and equations A11 amd A12 in ref. 13). Importantly, this CO2 balance does not depend on whether sulfuric acid reacts with carbonates or silicates. The short-term effect of weathering on the inorganic CO2 balance, [CO2]st, is (Extended Data Fig. 5a):
where [CO2] is the moles of CO2 produced (positive [CO2]) or sequestered (negative [CO2]) per unit volume of weathering fluid. Remembering that:
this equation can be simplified to:
Beyond the calcium carbonate compensation time (~10 kyr; ref. 62), the production of alkalinity and dissolved cations by chemical weathering is balanced by the precipitation of (mostly) marine calcium carbonate. Then, the medium-term effect of weathering on the inorganic CO2 balance, [CO2]mt, is (Extended Data Fig. 5b):
This equation can be simplified to:
We stress that equations (19) and (21) yield idealized estimates for the CO2 balance of weathering rates on timescales shorter and longer than the precipitation of calcium carbonate. These scenarios do not consider alkalinity consumption by reverse-weathering reactions63 or alkalinity production by sulfide reduction64, and they do not distinguish between alkalinity produced by weathering sodium, potassium or calcium silicates65. We also note that the timescale of ~10 kyr for carbonate precipitation in the ocean is only an estimate (although probably a maximum estimate). As argued above, some carbonate evidently precipitates once the water exits the subsurface. The location of precipitation is not directly relevant for the CO2 balance, but it will influence the timescales over which equations (19) and (21) apply. On multi-million-year timescales, for a system under constant boundary conditions and a carbon cycle in steady state, the long-term effect of weathering on the inorganic CO2 balance, [CO2]lt, may depend only on the calcium produced by silicate weathering1 (Extended Data Fig. 5c):
where \(\left[{\mathrm{Ca}}^{2 +} \right]_{\mathrm{sil}}^{\mathrm{eq}}\) is the equivalent calcium concentration from silicate weathering.
Carbonate equilibria
The saturation state of calcium carbonate in water (Ωcal) is defined as:
where Ksp is the equilibrium constant for the dissolution/precipitation reaction of calcium carbonate in water (Extended Data Table 2). By definition, the second dissociation constant of carbonic acid (K2):
It follows that
In order to convert the measured concentrations into activities, we calculated the activity coefficients γi for both calcium and bicarbonate using the Davies equation66:
where \(A = 1.82 \times 10^6\left( {\varepsilon T} \right)^{ - \frac{3}{2}}\) is an empirical constant, T is the temperature, ε is the dielectric constant and I is the ionic strength of the solution given by:
We estimated the dielectric constant using an empirical fit to measurements of the dielectric constant at atmospheric pressures and temperatures between 273.15 and 373.15 K (Table 4 in ref. 67):
The overall temperature dependence of the factor A in equation (26) is small and A ≈ 0.51.
We also estimated the equilibrium constant for reaction j at water temperature T (Kj,T) using the van’t Hoff equation68:
where Kj,298 is the equilibrium constant of reaction j at 298.15 K, \(\Delta H_j^ \circ\) is the standard enthalpy of reaction j and R is the ideal gas constant. The saturation index for calcium carbonate in water SIcal at temperature T (Extended Data Fig. 3) is then:
In addition to the saturation index, we estimated the pH at equilibrium (pHeq) using:
This pHeq (Fig. 3b) represents the pH of a solution that is exactly saturated with respect to the measured solutes. The value is a maximum estimate for the pH in the subsurface waters and the pH could, in principle, be lower. The presence of detrital carbonate in streams69 and carbonate precipitation around natural springs in the field suggests that carbonates are not strongly undersaturated in the subsurface. For all steps described above, uncertainties were propagated from the analytical uncertainties of measured concentrations. In these calculations, we considered the contributions of solutes only from weathering, cyclic sources and the secondary carbonate lost to precipitation. This procedure assumes that any hotspring input occurs in the stream, downstream of the weathering zone, and does not contribute substantially to the dissolved Sr2+ (Supplementary Text 4).
Estimate of pH change due to addition of sulfuric acid
We compared the inferred subsurface pH, pHeq, with the pH obtained by adding sulfuric acid to a carbonate-buffered solution, \({\mathrm{pH}}_{{\mathrm{SO}}_4}\). For simplicity, this particular calculation assumes that all sulfuric acid reacts with calcium carbonate, which is reasonable, particularly for the northern rivers in which carbonate weathering constitutes much more than half and up to >90% of the weathering budget. We define \({\mathrm{pH}}_{{\mathrm{SO}}_4}\) as the pH of a solution that results from the addition of sulfuric acid with concentration \(\left[{\mathrm{SO}}_4^{2 -} \right]\) to a calcium-carbonate-buffered solution with an initial pH noted as pH0. From equation (25), we recall that for a calcium-carbonate-buffered solution at equilibrium (that is, at Ωcal = 1), we have:
where the subscript 0 denotes the quantities before the addition of sulfuric acid. We further assume that the following reaction of sulfuric acid with calcium carbonate dominates:
and that \({\mathrm{HCO}}_3^{-}\) remains the dominant dissolved carbonate species (which is reasonable for the range of pH between 6 and 8). After addition of the acid, the new activity of protons at equilibrium with the acid is:
where the subscript f denotes the final quantities after equilibration with the acid. Hence:
Next, we link the initial concentration of calcium, \(\left[{\mathrm{Ca}}^{2 +} \right]_0\) and bicarbonate, \(\left[ {\mathrm{HCO}}_3^ - \right]_0,\) to the initial pH, pH0 (or initial activity of protons \(a_{\mathrm{H}^ + ,0}\)). Let \(\left[{\mathrm{CC}} \right]_0 = \left[{\mathrm{Ca}}^{2 +} \right]_0\left[{\mathrm{HCO}}_3^ - \right]_0\). Rearranging equation (33) we get:
Further, we posit that we can express the concentration of calcium before the addition of sulfuric acid as a function of the concentration of bicarbonate and vice versa:
and
where \(X_{{{\mathrm{Ca}}^{2+}},0}\) is the fraction of the total cation charge that is represented by calcium:
with
and
Equations (38)–(42) allow us to express the concentrations of calcium and bicarbonate by their total concentration [CC]0:
and
Now, the combination of equations (36), (43) and (44) yields:
and the final pH after addition of sulfuric acid is:
In our data analysis, we used equation (37) and an estimate of pH0 = 8.51 (see below for reasoning) to calculate [CC]0. Then, we calculated the pH change that is expected from pH0 due to the addition of sulfuric acid. We discarded 37 datapoints for which sulfate concentrations are larger than or within 10 µmol l−1 of the calcium concentrations (\(\left[ {\mathrm{Ca}}^{2 + } \right]_{\mathrm{f}} - 2\left[ {\mathrm{SO}}_4^{2 -} \right]\) < 10 μmol l−1). In these cases, the assumption that all sulfuric acid was buffered entirely by calcium carbonate dissolution is clearly inapplicable. Note that the factor of \(\sqrt {\frac{{X_{{\mathrm{Ca}}^{2 +},0}}}{2} + \frac{2}{{X_{{\mathrm{Ca}}^{2 +},0}}}}\) and, thus, the measured calcium \([{\mathrm{Ca}}^{2+}]_{\mathrm{f}}\) and inferred bicarbonate \(\left[ {\mathrm{HCO}}_3^ - \right]_f\) values have a very small effect on the final \({\mathrm{pH}}_{{\mathrm{SO}}_4}\). The main controls on \({\mathrm{pH}}_{{\mathrm{SO}}_4}\) are the initial pH and the concentration of sulfate. Thus, \({\mathrm{pH}}_{{\mathrm{SO}}_4}\) (equation (46)) is mostly independent of pHeq (equation (31)), except for the shared activity coefficients and equilibrium constants. We define the initial pH, pH0 = 8.51 (pH0 = 8.58 without secondary precipitation of calcite), as the unique value at which a regression through the data intersects the point \({\mathrm{pH}}_{{\mathrm{SO}}_4} = {\mathrm{pH}}_{\mathrm{eq}} = {\mathrm{pH}}_0\). This point represents the necessity that the subsurface pH before addition of sulfuric acid is equal to the initial pH. All uncertainties were propagated from the analytical uncertainties of measured concentrations. We note that bicarbonate contributions (used to calculate pHeq) were derived from a charge balance and are, therefore, negatively correlated with sulfate concentrations. In the case that we inadvertently ignore a major charge contributor (Supplementary Text 4), the correlation between the two pH estimates could be weakened.
All calculated quantities are reported in Supplementary Data 5.
Data availability
All data analysed in this study are available at https://doi.org/10.5880/GFZ.4.6.2021.001 (ref. 70).
Code availability
The MATLAB code used to implement the inversion of the geochemical data is available on request from the corresponding author.
Change history
25 March 2024
A Correction to this paper has been published: https://doi.org/10.1038/s41561-024-01426-0
References
Berner, R. A., Lasaga, A. C. & Garrels, R. M. The carbonate–silicate geochemical cycle and its effect on atmospheric carbon dioxide over the past 100 million years. Am. J. Sci. 283, 641–683 (1983).
Lasaga, A. C. Chemical kinetics of water–rock interactions. J. Geophys. Res. 89, 4009–4025 (1984).
Gabet, E. J. & Mudd, S. M. A theoretical model coupling chemical weathering rates with denudation rates. Geology 37, 151–154 (2009).
West, A. J., Galy, A. & Bickle, M. Tectonic and climatic controls on silicate weathering. Earth Planet. Sci. Lett. 235, 211–228 (2005).
Maher, K. & Chamberlain, C. P. Hydrologic regulation of chemical weathering and the geologic carbon cycle. Science 343, 1502–1504 (2014).
Riebe, C. S., Kirchner, J. W. & Finkel, R. C. Erosional and climatic effects on long-term chemical weathering rates in granitic landscapes spanning diverse climate regimes. Earth Planet. Sci. Lett. 224, 547–562 (2004).
Raymo, M. E. & Ruddiman, W. F. Tectonic forcing of late Cenozoic climate. Nature 359, 117–122 (1992).
Gaillardet, J., Dupré, B., Louvat, P. & Allègre, C. J. Global silicate weathering and CO2 consumption rates deduced from the chemistry of large rivers. Chem. Geol. 159, 3–30 (1999).
Maffre, P. et al. Mountain ranges, climate and weathering. Do orogens strengthen or weaken the silicate weathering carbon sink? Earth Planet. Sci. Lett. 493, 174–185 (2018).
Caves Rugenstein, J. K., Ibarra, D. E. & von Blanckenburg, F. Neogene cooling driven by land surface reactivity rather than increased weathering fluxes. Nature 571, 99–102 (2019).
Kump, L. R. & Arthur, M. A. in Tectonic Uplift and Climate Change (ed. Ruddiman, W. F.) 399–426 (Springer, 1997).
Hilton, R. G. & West, A. J. Mountains, erosion and the carbon cycle. Nat. Rev. Earth Environ. 1, 284–299 (2020).
Torres, M. A. et al. The acid and alkalinity budgets of weathering in the Andes–Amazon system: insights into the erosional control of global biogeochemical cycles. Earth Planet. Sci. Lett. 450, 381–391 (2016).
Calmels, D., Gaillardet, J., Brenot, A. & France-Lanord, C. Sustained sulfide oxidation by physical erosion processes in the Mackenzie River basin: climatic perspectives. Geology 35, 1003–1006 (2007).
Williamson, M. A. & Rimstidt, J. D. The kinetics and electrochemical rate-determining step of aqueous pyrite oxidation. Geochim. Cosmochim. Acta 58, 5443–5454 (1994).
Morse, J. W. & Arvidson, R. S. The dissolution kinetics of major sedimentary carbonate minerals. Earth Sci. Rev. 58, 51–84 (2002).
Sarin, M. M., Krishnaswami, S., Dilli, K., Somayajulu, B. L. K. & Moore, W. S. Major ion chemistry of the Ganga–Brahmaputra river system: weathering processes and fluxes to the Bay of Bengal. Geochim. Cosmochim. Acta 53, 997–1009 (1989).
Jacobson, A. D. & Blum, J. D. Relationship between mechanical erosion and atmospheric CO2 consumption in the New Zealand Southern Alps. Geology 31, 865–868 (2003).
Torres, M. A., West, A. J. & Li, G. Sulphide oxidation and carbonate dissolution as a source of CO2 over geological timescales. Nature 507, 346–349 (2014).
Mills, B. J. W. et al. Modelling the long-term carbon cycle, atmospheric CO2, and Earth surface temperature from late Neoproterozoic to present day. Gondwana Res. 67, 172–186 (2019).
Das, A., Chung, C.-H. & You, C.-F. Disproportionately high rates of sulfide oxidation from mountainous river basins of Taiwan orogeny: sulfur isotope evidence. Geophys. Res. Lett. 39, L12404 (2012).
Blattmann, T. M. et al. Sulphuric acid-mediated weathering on Taiwan buffers geological atmospheric carbon sinks. Sci. Rep. 9, 2945 (2019).
Guo, J. et al. Reconciling chemical weathering rates across scales: application of uranium-series isotope systematics in volcanic weathering clasts from Basse-Terre Island (French Guadeloupe). Earth Planet. Sci. Lett. 530, 115874 (2019).
Godsey, S. E., Hartmann, J. & Kirchner, J. W. Catchment chemostasis revisited: water quality responds differently to variations in weather and climate. Hydrol. Process. 33, 3056–3069 (2019).
Ramsey, L. A., Walker, R. T. & Jackson, J. Geomorphic constraints on the active tectonics of southern Taiwan. Geophys. J. Int. 170, 1357–1372 (2007).
Fellin, M. G., Chen, C.-Y., Willett, S. D., Christl, M. & Chen, Y.-G. Erosion rates across space and timescales from a multi-proxy study of rivers of eastern Taiwan. Glob. Planet. Change 157, 174–193 (2017).
Chen, C.-Y. et al. The impact of storm-triggered landslides on sediment dynamics and catchment-wide denudation rates in the southern Central Range of Taiwan following the extreme rainfall event of Typhoon Morakot. Earth Surf. Proc. Land. 45, 548–564 (2020).
Dadson, S. J. et al. Links between erosion, runoff variability and seismicity in the Taiwan orogen. Nature 426, 648–651 (2003).
Lee, C.-H., Chen, W.-P. & Lee, R.-H. Estimation of groundwater recharge using water balance coupled with base-flow-record estimation and stable-base-flow analysis. Environ. Geol. 51, 73–82 (2006).
Lin, C.-W. & Chen, W.-S. Geologic Map of Taiwan (Geological Society of Taiwan, 2016).
Gu, X. et al. Chemical reactions, porosity, and microfracturing in shale during weathering: the effect of erosion rate. Geochim. Cosmochim. Acta 269, 63–100 (2020).
Kanzaki, Y., Brantley, S. L. & Kump, L. R. A numerical examination of the effect of sulfide dissolution on silicate weathering. Earth Planet. Sci. Lett. 539, 116239 (2020).
Emberson, R., Galy, A. & Hovius, N. Weathering of reactive mineral phases in landslides acts as a source of carbon dioxide in mountain belts. J. Geophys. Res. 123, 2695–2713 (2018).
Ibarra, D. E. et al. Modeling the consequences of land plant evolution on silicate weathering. Am. J. Sci. 319, 1–43 (2019).
Gudbrandsson, S., Wolff-Boenisch, D., Gislason, S. R. & Oelkers, E. H. Experimental determination of plagioclase dissolution rates as a function of its composition and pH at 22 °C. Geochim. Cosmochim. Acta 139, 154–172 (2014).
Wilke, F. D. H., Vieth-Hillebrand, A., Naumann, R., Erzinger, J. & Horsfield, B. Induced mobility of inorganic and organic solutes from black shales using water extraction: implications for shale gas exploitation. Appl. Geochem. 63, 158–168 (2015).
Moon, S., Chamberlain, C. P. & Hilley, G. E. New estimates of silicate weathering rates and their uncertainties in global rivers. Geochim. Cosmochim. Acta 134, 257–274 (2014).
Milliman, J. D., Lee, T. Y., Huang, J. C. & Kao, S. J. Impact of catastrophic events on small mountainous rivers: temporal and spatial variations in suspended- and dissolved-solid fluxes along the Choshui River, central western Taiwan, during Typhoon Mindulle, July 2–6, 2004. Geochim. Cosmochim. Acta 205, 272–294 (2017).
Lee, Y.-J., Chen, P.-H., Lee, T.-Y., Shih, Y.-T. & Huang, J.-C. Temporal variation of chemical weathering rate, source shifting and relationship with physical erosion in small mountainous rivers, Taiwan. Catena 190, 104516 (2020).
Hercod, D. J., Brady, P. V. & Gregory, R. T. Catchment-scale coupling between pyrite oxidation and calcite weathering. Chem. Geol. 151, 259–276 (1998).
Herlihy, A. T. & Mills, A. L. Sulfate reduction in freshwater sediments receiving acid mine drainage. Appl. Environ. Microbiol. 49, 179–186 (1985).
Kwong, Y. T. J., Whitley, G. & Roach, P. Natural acid rock drainage associated with black shale in the Yukon Territory, Canada. Appl. Geochem. 24, 221–231 (2009).
Marx, A. et al. A review of CO2 and associated carbon dynamics in headwater streams: a global perspective. Rev. Geophys. 55, 560–585 (2017).
Bookhagen, B. & Burbank, D. W. Topography, relief, and TRMM-derived rainfall variations along the Himalaya. Geophys. Res. Lett. 33, L08405 (2006).
Larsen, I. J., Montgomery, D. R. & Greenberg, H. M. The contribution of mountains to global denudation. Geology 42, 527–530 (2014).
Turchyn, A. V. & Schrag, D. P. Oxygen isotope constraints on the sulfur cycle over the past 10 million years. Science 303, 2004–2007 (2004).
Galy, V. et al. Efficient organic carbon burial in the Bengal fan sustained by the Himalayan erosional system. Nature 450, 407–410 (2007).
Lupker, M. et al. Predominant floodplain over mountain weathering of Himalayan sediments (Ganga basin). Geochim. Cosmochim. Acta 84, 410–432 (2012).
Macdonald, F. A., Swanson-Hysell, N. L., Park, Y., Lisiecki, L. & Jagoutz, O. Arc–continent collisions in the tropics set Earth’s climate state. Science 364, 181–184 (2019).
Resentini, A., Goren, L., Castelltort, S. & Garzanti, E. Partitioning sediment flux by provenance and tracing erosion patterns in Taiwan. J. Geophys. Res. 122, 1430–1454 (2017).
Ramsey, L. A., Hovius, N., Lague, D. & Liu, C.-S. Topographic characteristics of the submarine Taiwan orogen. J. Geophys. Res. 111, F02009 (2006).
Lague, D. The stream power river incision model: evidence, theory and beyond. Earth Surf. Proc. Land. 39, 38–61 (2014).
Schwanghart, W. & Scherler, D. Short communication: TopoToolbox 2 – MATLAB-based software for topographic analysis and modeling in Earth surface sciences. Earth Surf. Dynam. 2, 1–7 (2014).
Ho, C. S. A synthesis of the geologic evolution of Taiwan. Tectonophysics 125, 1–16 (1986).
Burke, A. et al. Sulfur isotopes in rivers: insights into global weathering budgets, pyrite oxidation, and the modern sulfur cycle. Earth Planet. Sci. Lett. 496, 168–177 (2018).
Bickle, M. J., Tipper, E., Galy, A., Chapman, H. & Harris, N. On discrimination between carbonate and silicate inputs to Himalayan rivers. Am. J. Sci. 315, 120–166 (2015).
Nehrke, G., Reichart, G. J., Van Cappellen, P., Meile, C. & Bijma, J. Dependence of calcite growth rate and Sr partitioning on solution stoichiometry: non-Kossel crystal growth. Geochim. Cosmochim. Acta 71, 2240–2249 (2007).
Gabitov, R. I. & Watson, E. B. Partitioning of strontium between calcite and fluid. Geochem. Geophys. Geosyst. 7, Q11004 (2006).
Tesoriero, A. J. & Pankow, J. F. Solid solution partitioning of Sr2+, Ba2+, and Cd2+ to calcite. Geochim. Cosmochim. Acta 60, 1053–1063 (1996).
Loste, E., Wilson, R. M., Seshadri, R. & Meldrum, F. C. The role of magnesium in stabilising amorphous calcium carbonate and controlling calcite morphologies. J. Cryst. Growth 254, 206–218 (2003).
Meldrum, F. C. & Hyde, S. T. Morphological influence of magnesium and organic additives on the precipitation of calcite. J. Cryst. Growth 231, 544–558 (2001).
Zeebe, R. E. & Westbroek, P. A simple model for the CaCO3 saturation state of the ocean: the ‘Strangelove,’ the ‘Neritan,’ and the ‘Cretan’ Ocean. Geochem. Geophys. Geosyst. 4, 1104 (2003).
Garrels, R. M. Silica: role in the buffering of natural waters. Science 148, 69 (1965).
Jørgensen, B. B. Mineralization of organic matter in the sea bed—the role of sulphate reduction. Nature 296, 643–645 (1982).
France-Lanord, C. & Derry, L. A. Organic carbon burial forcing of the carbon cycle from Himalayan erosion. Nature 390, 65–67 (1997).
Davies, C. W. Ion Association (Butterworths, 1962).
Archer, D. G. & Wang, P. The dielectric constant of water and Debye–Hückel limiting law slopes. J. Phys. Chem. Ref. Data 19, 371–411 (1990).
van’t Hoff, M. J. H. Etudes de Dynamique Chimique (Frederik Muller & Company, 1884).
Garzanti, E. & Resentini, A. Provenance control on chemical indices of weathering (Taiwan river sands). Sediment. Geol. 336, 81–95 (2016).
Bufe, A. et al. Major Element Stream Water Chemistry, Compiled 10Be Erosion Rates, and Analyses of Weathering Across an Erosion-rate Gradient in in Southern Taiwan (GFZ Data Services, 2021); https://doi.org/10.5880/GFZ.4.6.2021.001
Parkhurst, D. L. & Appelo, C. User’s Guide to PHREEQC (Version 2): A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations Water-Resources Investigations Report 99-4259 (US Geological Survey, 1999).
Acknowledgements
This research was enabled by resources from the Initiative and Networking Fund of the Helmholtz Association. A.B. was supported by an EU Marie Skłodowska-Curie Research Fellowship (no. 841663). J.K.C.R. was supported by an ETH Fellowship and an Alexander von Humboldt Fellowship. We thank C. Zorn, B. Zimmermann, J. Schlegel, D. Frick, A. Gottsche and the HELGES Lab for laboratory assistance; and J. Bouchez and F. v. Blanckenburg for valuable discussions.
Funding
Open access funding provided by Helmholtz-Zentrum Potsdam Deutsches GeoForschungsZentrum - GFZ (4217).
Author information
Authors and Affiliations
Contributions
N.H., R.E. and A.B. conceived the study; A.B., R.E., H.J.H.-G. and N.H. contributed samples and laboratory analyses; A.B. led the data analysis with contributions from J.K.C.R., N.H., R.E. and A.G., and the writing of the manuscript with contributions from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Geoscience thanks Jérôme Gaillardet, Lee Kump and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Clare Davis; Rebecca Neely.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Normalized steepness index and erosion rates.
Scaling between catchment-averaged steepness index and catchment-averaged erosion rates from published 10Be cosmogenic nuclide data. Red line shows regression through data from before and from at least 6 years after Typhoon Morakot (red points) and 95% confidence band. Three outliers, all located in the Mutan formation (see Fig. 1) were excluded. If they were included, the inferred erosion rate gradient across the study area would be even wider. Symbols mark dominant lithology (see Fig. 1). Error bars are equivalent to a 95% confidence interval.
Extended Data Fig. 2 Inversion results including hotspring and cyclic contributions.
Symbology is equivalent to Fig. 2. Error bars are equivalent to a 95% confidence interval.
Extended Data Fig. 3 Saturation index.
Saturation index of samples corrected for secondary precipitation (blue) and uncorrected for secondary precipitation (grey). Symbols mark dominant lithology (see Fig. 1). Error bars are equivalent to a 95% confidence interval. Samples with anomalously high sulfate concentrations are marked as darker points.
Extended Data Fig. 4 Variations of total dissolved solid concentrations between sampling seasons.
Total dissolved solid values for samples collected in 2017 and 2015. Both sampling seasons include samples from across the erosion rate gradient. Whereas the drier year of 2015 was characterized by somewhat higher concentrations, both distributions are within one standard deviation.
Extended Data Fig. 5 Impact of weathering on the CO2-balance.
Moles of CO2 emitted or sequestered per volume of water plotted against catchment-averaged steepness index (lower x-axis) and inferred erosion rates (upper x-axis) for different scenarios and timescales. a, Impact of weathering reactions only. b, Impact of weathering reactions and carbonate precipitation. c, Impact of only Ca-silicate weathering. Symbols mark dominant lithology (see Fig. 1). Error bars are equivalent to a 95% confidence interval.
Extended Data Fig. 6 Mixing diagram for weathering contributions.
a, Mg2+/Ca2+ – Na+/Ca2+ mixing diagram showing raw data (grey) and weathering contributions (red). Blue points mark endmembers with two standard deviations. Dark-red squares are available hotspring data. Purple points are the suspended sediment data from the Chenyoulan. The grey lines are the best fit endmember mixing lines found by the inverse approach. b, Close-up of panel a. Symbols mark dominant lithology (see Fig. 1). Error bars are equivalent to a 95% confidence interval.
Extended Data Fig. 7 Correction for secondary precipitation.
a, Stream water chemistry including contributions from rainwater and weathering coloured by erosion rate. All purple suspended sediment data are used to define the endmember trend (purple line with 95% confidence bands), and all data above that line are projected onto that line. b, Stream water chemistry corrected for secondary precipitation of calcite. Only points above the mixing line were corrected. Symbols mark dominant lithology (see Fig. 1). Error bars are equivalent to a 95% confidence interval.
Supplementary information
Supplementary information
Supplementary Text 1–4 and Figs. 1–8.
Supplementary Data
Supplementary Data 1–5.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bufe, A., Hovius, N., Emberson, R. et al. Co-variation of silicate, carbonate and sulfide weathering drives CO2 release with erosion. Nat. Geosci. 14, 211–216 (2021). https://doi.org/10.1038/s41561-021-00714-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41561-021-00714-3
This article is cited by
-
Deep CO2 release and the carbon budget of the central Apennines modulated by geodynamics
Nature Geoscience (2024)
-
Resolving controversies surrounding carbon sinks from carbonate weathering
Science China Earth Sciences (2024)
-
Alkalinity responses to climate warming destabilise the Earth’s thermostat
Nature Communications (2023)
-
Hydrochemistry and carbon isotope characteristics of Nujiang River water: Implications for CO2 budgets of rock weathering in the Tibetan Plateau
Science China Earth Sciences (2023)
-
Impact of stylolite cementation on weathering rates of carbonate rocks
Carbonates and Evaporites (2023)