Abstract
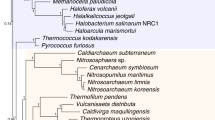
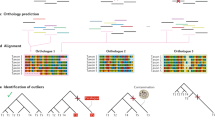
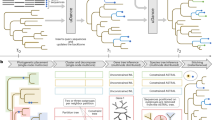
Ancestor–descendent relations play a cardinal role in evolutionary theory. Those relations are determined by rooting phylogenetic trees. Existing rooting methods are hampered by evolutionary rate heterogeneity or the unavailability of auxiliary phylogenetic information. Here we present a rooting approach, the minimal ancestor deviation (MAD) method, which accommodates heterotachy by using all pairwise topological and metric information in unrooted trees. We demonstrate the performance of the method, in comparison to existing rooting methods, by the analysis of phylogenies from eukaryotes and prokaryotes. MAD correctly recovers the known root of eukaryotes and uncovers evidence for the origin of cyanobacteria in the ocean. MAD is more robust and consistent than existing methods, provides measures of the root inference quality and is applicable to any tree with branch lengths.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Fitch, W. M. & Margoliash, E. Construction of phylogenetic trees. Science 155, 279–284 (1967).
Ragan, M. A. Trees and networks before and after Darwin. Biol. Direct 4, 43 (2009).
Kluge, A. G. & Farris, J. S. Quantitative phyletics and the evolution of anurans. Syst. Biol. 18, 1–32 (1969).
Farris, J. S. Estimating phylogenetic trees from distance matrices. Am. Nat. 106, 645–668 (1972).
Lepage, T., Bryant, D., Philippe, H. & Lartillot, N. A general comparison of relaxed molecular clock models. Mol. Biol. Evol. 24, 2669–2680 (2007).
Williams, T. A. et al. New substitution models for rooting phylogenetic trees. Phil. Trans. R. Soc. B 370, 20140336 (2015).
Stechmann, A. & Cavalier-Smith, T. Rooting the eukaryote tree by using a derived gene fusion. Science 297, 89–91 (2002).
Katz, L. A., Grant, J. R., Parfrey, L. W. & Burleigh, J. G. Turning the crown upside down: gene tree parsimony roots the eukaryotic tree of life. Syst. Biol. 61, 653–660 (2012).
Guindon, S. et al. New algorithms and methods to estimate maximum-likelihood phylogenies: assessing the performance of PhyML 3.0. Syst. Biol. 59, 307–321 (2010).
Ronquist, F. et al. MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space. Syst. Biol. 61, 539–542 (2012).
Bapteste, E. et al. Prokaryotic evolution and the tree of life are two different things. Biol. Direct 4, 34 (2009).
Turner, S., Pryer, K. M., Miao, V. P. W. & Palmer, J. D. Investigating deep phylogenetic relationships among cyanobacteria and plastids by small subunit rRNA sequence analysis. J. Eukaryot. Microbiol. 46, 327–338 (1999).
Shih, P. M. et al. Improving the coverage of the cyanobacterial phylum using diversity-driven genome sequencing. Proc. Natl Acad. Sci. USA 110, 1053–1058 (2013).
Dagan, T. et al. Genomes of stigonematalean cyanobacteria (subsection V) and the evolution of oxygenic photosynthesis from prokaryotes to plastids. Genome Biol. Evol. 5, 31–44 (2013).
Huerta-Cepas, J. et al. eggNOG 4.5: a hierarchical orthology framework with improved functional annotations for eukaryotic, prokaryotic and viral sequences. Nucleic Acids Res. 44, D286–D293 (2016).
O’Leary, N. A. et al. Reference sequence (RefSeq) database at NCBI: current status, taxonomic expansion, and functional annotation. Nucleic Acids Res. 44, D733–D745 (2016).
Markowitz, V. M. et al. IMG 4 version of the integrated microbial genomes comparative analysis system. Nucleic Acids Res. 42, D560–D567 (2014).
Altschul, S. F., Gish, W., Miller, W., Myers, E. W. & Lipman, D. J. Basic local alignment search tool. J. Mol. Biol. 215, 403–410 (1990).
Tatusov, R. L., Koonin, E. V. & Lipman, D. J. A genomic perspective on protein families. Science 278, 631–637 (1997).
Rice, P., Longden, I. & Bleasby, A. EMBOSS: the European molecular biology open software suite. Trends Genet. 16, 276–277 (2000).
Enright, A. J., Van Dongen, S. & Ouzounis, C. A. An efficient algorithm for large-scale detection of protein families. Nucleic Acids Res. 30, 1575–1584 (2002).
Thiergart, T., Landan, G. & Martin, W. F. Concatenated alignments and the case of the disappearing tree. BMC Evol. Biol. 14, 266 (2014).
Katoh, K. & Standley, D. M. MAFFT multiple sequence alignment software version 7: improvements in performance and usability. Mol. Biol. Evol. 30, 772–780 (2013).
Author information
Authors and Affiliations
Contributions
We thank D. Bryant, A. Kupczok and M. Wilkinson for critical comments on the manuscript. We acknowledge support from the European Research Council (grant no. 281375) and CAPES (Coordination for the Improvement of Higher Education Personnel–Brazil).
T.D., G.L. and F.D.K.T. conceived the study. F.D.K.T. and G.L. developed and implemented the method. F.D.K.T. performed all analyses. T.D., G.L. and F.D.K.T. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figure 1; Supplementary Tables 1 and 2. (PDF 221 kb)
Supplementary Table 3
Species composition in the three datasets. (XLS 59 kb)
Rights and permissions
About this article
Cite this article
Tria, F., Landan, G. & Dagan, T. Phylogenetic rooting using minimal ancestor deviation. Nat Ecol Evol 1, 0193 (2017). https://doi.org/10.1038/s41559-017-0193
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41559-017-0193
This article is cited by
-
Phylogenomic profiles of whole-genome duplications in Poaceae and landscape of differential duplicate retention and losses among major Poaceae lineages
Nature Communications (2024)
-
Stepwise pathway for early evolutionary assembly of dissimilatory sulfite and sulfate reduction
The ISME Journal (2023)
-
Replicated life-history patterns and subsurface origins of the bacterial sister phyla Nitrospirota and Nitrospinota
The ISME Journal (2023)
-
Common loss of far-red light photoacclimation in cyanobacteria from hot and cold deserts: a case study in the Chroococcidiopsidales
ISME Communications (2023)
-
Phylogenomic insights into the polyphyletic nature of Altai falcons within eastern sakers (Falco cherrug) and the origins of gyrfalcons (Falco rusticolus)
Scientific Reports (2023)