Abstract
It has been argued that the −5 °C annual mean 2 m air temperature isotherm defines a limit of ice shelf viability on the Antarctic Peninsula as melt ponding increases at higher temperatures. It is, however, presently unknown whether this threshold can also be applied to other Antarctic ice shelves. Here we use two present-day and three future high-resolution Antarctic climate simulations to predict warming thresholds for Antarctic ice shelf melt pond formation on the basis of the melt-over-accumulation ratio. The associated warming thresholds match well with observed melt pond volumes and are found to be spatially highly variable and controlled by snow accumulation. For relatively wet ice shelves, the −5 °C temperature threshold was confirmed; but cold and dry ice shelves such as Amery, Ross and Filchner-Ronne are more vulnerable than previously thought, with threshold temperatures well below −15 °C. Coupled Model Intercomparison Project Phase 6 models predict that towards the end of this century these thresholds can be reached on many ice shelves, even on cold ice shelves and under moderate warming scenarios.
Similar content being viewed by others
Main
Several processes have been identified that precede the disintegration of Antarctic ice shelves, the floating extensions of the Antarctic ice sheet (AIS). At the ice shelf–ocean interface, the warming of intermediate-depth waters increases basal melting, leading to ice shelf thinning, weakening and damage, which is currently driving the break-up of the Thwaites Eastern ice shelf in West Antarctica1. At the ice shelf–atmosphere interface, atmospheric warming increases surface melt rates along the entire margin of the AIS, most notably over the low-lying, floating ice shelves2,3,4. The additional meltwater can lead to firn air depletion, ponding and subsequent ice shelf hydrofracturing and disintegration5,6,7,8, the latter often in combination with enhanced ocean swell and atmospheric river activity9. Ice shelf hydrofracturing also requires the presence of deep, pre-existing crevasses, which applies to most of the Antarctic ice shelf area8. In the eastern Antarctic Peninsula (AP), a considerable fraction of ice shelves has (partly) disintegrated following extensive melt ponding, such as the Larsen A and Larsen B ice shelves in 1995 and 2002, respectively10,11. There are concerns that future warming and associated melt increases will cause more ice shelves to disintegrate in the AP as well as elsewhere in Antarctica, leading to enhanced mass loss where ice shelves buttress grounded ice and an acceleration in sea level rise. In this study, we present AIS-wide temperature thresholds for melt pond formation, a necessary condition for the potential hydrofracture of Antarctic ice shelves, and explore to what extent these thresholds have been passed or will be passed in the future.
Temperature thresholds for meltwater ponding
The impact of atmospheric forcing on ice shelf viability in the AP was previously quantified by Morris and Vaughan12, who showed that ice shelves situated at the warm side of the −9 °C annual mean surface temperature isotherm are susceptible to meltwater ponding and disintegration, and that no ice shelves exist above −5 °C in this region. It is presently unknown whether these thresholds can also be applied to other Antarctic ice shelves. An alternative method to predict the onset of meltwater ponding considers the formation (by snow accumulation) and demise (by refreezing and densification) of firn air content5. Theoretical considerations imply that when the melt-over-accumulation (MOA) ratio exceeds 0.7, firn pore space can no longer be maintained, and meltwater runoff and/or ponding is initiated13,14. This threshold, when calculated using contemporary (1979–2018) output of a high-resolution (5.5 km) polar regional climate model (RACMO2.3p2), accurately predicts the viability threshold for ice shelves in the eastern AP (Supplementary Fig. 1b), but for temperatures that are typically lower than the thresholds mentioned above (Supplementary Fig. 1a). This suggests that a universal temperature threshold for all Antarctic ice shelves does not exist.
An advantage of using the MOA = 0.7 threshold is that the effects of snow accumulation and liquid water availability (melt and rain, henceforth referred to as melt for readability), which are both expected to increase in Antarctica in a warming climate, can be separately quantified. This is relevant because model studies suggest that Antarctic-wide snow accumulation increases quasi-linearly with temperature, in first order following the Clausius–Clapeyron relationship15,16, but with large regional variations owing to changes in precipitation phase and large-scale circulation14,17,18. In contrast, surface melt is expected to increase more strongly than linear with temperature19 because of several feedback mechanisms, such as the snowmelt–albedo feedback20, the wind–albedo interaction21 and/or the poorly understood impacts of ice clouds and water clouds on rainfall22 and surface melt23. We thus expect a non-trivial response of MOA to future warming.
The goal of this study is to include these feedbacks when calculating the spatial distribution of the MOA = 0.7 threshold, while still being able to use low-resolution Coupled Model Intercomparison Project Phase 6 (CMIP6) models that often represent Antarctic temperature reasonably well, but not accumulation and/or melt, owing to lacking resolution and/or snow physics. To that end, we used five contemporary and future AIS-wide climate realizations from the high-resolution, polar regional climate model RACMO2.3p2 to robustly fit annual totals of snow accumulation and melt to annual average 2 m air temperature (T2m). The climate realizations used are one observationally constrained simulation for the present day (R-ERA5, 1979–2021) and four simulations forced by the Community Earth System Model Version 2 (CESM2): one historical (R-HIST, 1950–2014) and three different future emission pathways extending to 2100 (R-CESM2; SSP1-2.6, SSP2-4.5 and SSP5-8.5). We calculated the MOA = 0.7 threshold temperature (TT) and uncertainty (dTT) for groups of ice shelves (Fig. 1), individual ice shelves (Fig. 2, Extended Data Fig. 1 and Supplementary Fig. 3) and individual RACMO2.3p2 grid cells (27 × 27 km2, Fig. 3 and Extended Data Fig. 2).
a,b, Annual ice shelf average surface melt rate (filled dots) and accumulation (open dots) for R-ERA5 (black), R-HIST (blue), R-126 (green), R-245 (yellow) and R-585 (red) (in mm w.e. per year) as a function of T2m for cold (contemporary (1979–2021, R-ERA5) T2m < −15 °C) and dry (contemporary accumulation (A) < 500 mm w.e. per year) (a) and mild (T2m > −15 °C) and wet (A > 500 mm w.e. per year) (b) climatic conditions. The selected climatic thresholds are medians—that is, just as many ice shelves fall in the cold and dry as in the wet and mild category. The resulting fits of melt and accumulation are shown by solid lines, their upper and lower uncertainty (±1σ) are shown by dashed lines, and the resulting TT ± dTT is shown in the lower right corner. The vertical dashed line represents the MOA = 0.7 intersection at T2m = TT. See the Methods for more details.
Ice shelf average threshold temperature to reach MOA = 0.7, as a function of R-ERA5 average present-day (1979–2021) accumulation in mm w.e. per year. The colours represent R-ERA5 present-day surface melt rates (mm w.e. per year). Some specific ice shelves are highlighted, and only major ice shelves (>800 km2) are shown. The square boxes represent the average conditions presented in Fig. 1. The vertical error bars denote the uncertainty in TT (dTT, one standard deviation as described in the Methods), and the horizontal error bars indicate the uncertainty in accumulation (10% of the present-day mean accumulation3). The horizontal dashed lines represent the −9 and −5 °C isotherms commonly applied to AP ice shelves12. The black line is a power-law fit of TT as a function of accumulation, with the fit parameters, R2 and root mean square error (RMSE) denoted in the figure text.
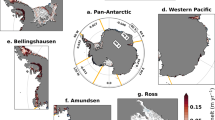
a, Intersect values of T2m for which the MOA = 0.7 threshold is reached (TT). The values are calculated at all grid points that have melt rates greater than 0.01 mm w.e. per year in any of the model runs. Ice shelves mentioned in the text are denoted. b, The T2m increase (ΔT) needed to reach the MOA = 0.7 threshold (TT), with respect to the base climate (1979–2021) from R-ERA5. Values below zero (ΔT < 0, yellow) denote locations where TT has already been reached in the present day.
Thresholds controlled by snow accumulation
The temperature threshold (TT) for Antarctic ice shelves grouped in two distinct present-day (R-ERA5, 1979–2021) climate regimes is presented in Fig. 1: relatively dry and cold (snow accumulation < 500 mm water equivalent (w.e.) per year; T2m < −15 °C), and relatively wet and mild (snow accumulation > 500 mm w.e. per year; T2m > −15 °C). For the dry and cold ice shelves, MOA = 0.7 is reached at TT = −13.4 ± 0.2 °C; for the mild and wet ice shelves, it is reached at TT = −9.0 ± 0.2 °C. While the latter value equals the lower AP temperature threshold proposed in ref. 12, the value for the cold and dry ice shelves is considerably lower, as the lower accumulation rates enable the threshold to be reached at a lower temperature. Note that above −10 °C (red dots in Fig. 1b), the dependency of snow accumulation on temperature decreases, a result of increased rainfall at the expense of snowfall under these warmer conditions.
The values of TT determined individually for all 56 major Antarctic ice shelves as a function of present-day (1979–2021) snow accumulation are presented in Fig. 2. TT asymptotically converges to values around −5 °C, which suggests that the AP temperature thresholds can be applied to wetter Antarctic ice shelves but not to colder and drier ice shelves. The strong increase of TT with accumulation highlights the pivotal role of fresh snow in buffering meltwater and keeping the surface bright, reducing the strength of the snowmelt–albedo feedback. Melt rate does not predict the warming threshold as skilfully, because the melt fits are comparable for most ice shelves (Extended Data Fig. 1).
TT on the scale of individual 27 × 27 km2 grid cells is presented in Fig. 3a, with values higher than −9 °C found in relatively warm and wet coastal regions, mostly in West Antarctica and the western AP. Colder and drier conditions with lower TT values around −12 °C are found in the eastern AP and coastal East Antarctica. The lowest TT values, less than −15 °C, are found on the coldest and driest ice shelves, such as Filchner-Ronne, Ross and Amery. Climate and thus the warming threshold can also vary substantially within individual ice shelves. On the Ross ice shelf, TT is distributed relatively uniformly, but Amery and Filchner-Ronne show larger spatial variability, with TT generally increasing towards the seaward parts of the ice shelves, which are generally wetter.
Observations confirm modelled thresholds
There is a high correspondence of low/negative values of ΔT (the increase in contemporary T2m required to reach the warming threshold (Fig. 3b)) with high observed supraglacial meltwater volume (Methods, Extended Data Fig. 3 and Supplementary Fig. 2). The regional variability of ΔT is large, even on individual ice shelves. On the furthest-inland parts of the Amery ice shelf, where accumulation and TT are the lowest, ΔT is close to zero, which is confirmed by observations of extensive meltwater ponding24 (Extended Data Fig. 3) and tidally induced hydrofracturing25. In contrast, towards the northwestern parts of the Amery ice shelf, accumulation rates increase, and approximately five degrees of warming is needed to reach the warming threshold.
Further east along the coast of East Antarctica, the Shackleton ice shelf also has considerably positive ΔT values and low observed melt pond volumes on the relatively wet western part, decreasing to ΔT < 0 further east, as confirmed by ubiquitous melt ponds26. Just east of the Shackleton ice shelf, we find ΔT < 0 on the Conger ice shelf, which has been gradually retreating since the 1970s, the last part breaking up in March 2022. Further east still, ice shelves along Sabrina Coast also have small ΔT values and high observed melt pond volumes (Extended Data Fig. 3), suggesting that they are also close to or beyond the warming threshold, in line with, for example, the 2007 retreat of the Voyeykov ice shelf27.
The Fimbul and Roi Baudouin ice shelves in Dronning Maud Land show the lowest ΔT values near their grounding lines and higher values further seaward. The region near the grounding line is characterized by strong melt–albedo feedbacks causing meltwater flow, ponding and englacial water storage21. In the relatively mild AP, some ice shelves have also passed the threshold for melt pond formation (ΔT < 0): the remnants of Larsen B, northern Larsen C, northern George VI and dry inland parts of Wilkins and Bach. Most other AP ice shelves show small positive ΔT values—that is, they only require little additional warming to reach TT. This is different for coastal West Antarctica, where TT is high, ΔT relatively large and the currently observed melt pond volumes low. On the Getz, Abbot and Venable ice shelves, considerable warming (ΔT > 5 °C) is needed to reach the threshold. Only the dry section of the Abbot ice shelf in the lee of Thurston Island shows lower ΔT values. In summary, the ΔT = 0 threshold derived here robustly detects observed melt ponds in coastal Antarctica, which is further supported by a quantitative comparison of ΔT with observed melt pond volumes as well as two previously reported products of melt pond concentrations26,28 (Supplementary Fig. 2).
Apart from locations where closed basins form in response to underlying bedrock topography, meltwater ponding is less likely to occur over grounded ice, where the surface slope induces downslope runoff, amplifying the availability of liquid water and the ponding potential over the adjacent ice shelf. Moreover, for most of the elevated interior, ice sheet melt remains small, and a meaningful warming threshold (hence ΔT) cannot be calculated (Fig. 3). Notable exceptions are the grounded ice sheet regions south of Amery and east of Ross. Over the Amery ice shelf, persistent meltwater flow over grounded ice and pond formation over the adjacent ice shelf were confirmed by ref. 26. For the large, relatively gently sloping grounded ice in West Antarctica east of the Ross ice shelf, ΔT values are relatively small and similar to those on the ice shelf, implying a notable potential for enhanced meltwater runoff from the grounded ice sheet onto the eastern Ross ice shelf in a future climate that is only moderately (~3–4 °C) warmer.
Future melt ponding potential
To assess future melt pond formation, we used T2m projections for the end of the century (2090–2100), averaged over individual ice shelves, from the full suite (N = 41) of CMIP6 models. The results for seven selected ice shelves that are large enough to be resolved by the low-resolution CMIP6 model grids (typically ~100 km) are presented in Fig. 4. The three largest and coldest ice shelves (Ross, Filchner-Ronne and Amery) are predicted to react very differently to future warming: even in the strongest warming scenario, the Filchner-Ronne ice shelf does not reach the warming threshold (TT) (for simplicity taken here as the median CMIP6 warming reaching the average TT value). In contrast, the warming threshold is reached for the Ross ice shelf for both the SSP5-8.5 and SSP3-7.0 warming scenarios. For the Amery ice shelf, with the lowest threshold temperature, all emission scenarios result in the warming threshold being passed by a significant margin.
Ice shelf average TT to reach MOA = 0.7 (solid lines) and spatial variability (dashed lines; 1σ of all ice shelf grid points) of the Ross, Filchner-Ronne, Amery, Shackleton, Baudouin, Larsen C and Getz ice shelves. The end-of-century (2090–2100) average T2m for R-CESM2 (SSP1-2.6, SSP2-4.5 and SSP5-8.5) (black stars) and end-of-century T2m box plots for the full CMIP6 ensemble of SSP1-2.6 (blue, 40 models), SSP2-4.5 (green, 40 models), SSP3-7.0 (yellow, 36 models) and SSP5-8.5 (red, 41 models) are shown. The boxes represent the 33–67% percentiles, the middle line represents the median and the whiskers represent the 10–90% percentiles. Also shown for each ice shelf are the average 1979–2021 R-ERA5 (open circles) and 1950–2014 R-HIST (solid circles) T2m, and (in text) the 1979–2021 R-ERA5 average snow accumulation (A).
The responses of the four selected warmer ice shelves are also very different. For the Shackleton and Larsen C ice shelves, the warming threshold will be passed in all warming scenarios, and for Roi Baudouin in all but the coldest scenario. For the Larsen C ice shelf, the warming threshold will be passed even in the strongest mitigation scenario. In contrast, despite it currently being one of the warmest ice shelves, Getz is also the most resilient and is not projected to reach the warming threshold this century in any of the warming scenarios. Not only its recent but also its future thinning will therefore largely depend on ocean influences.
Discussion
These results show that snow accumulation rates control the atmospheric warming threshold for surface melt pond formation, a prerequisite for the hydrofracture of Antarctic ice shelves. Our approach to calculating these warming thresholds involves historical, contemporary and future regional climate model realizations. The model used (RACMO2.3p2) is known to realistically simulate the contemporary climate and surface mass balance of the AIS, and the chosen method (which uses temperature fits to all available data) ensures that the threshold values obtained are less sensitive to the choice of the individual model realizations or the forcing model. Changing the MOA threshold to, for example, MOA = 1.0 (which reflects the situation where more snow mass is melted than is gained) simply increases TT but does not fundamentally change its spatial variability or its dependency on accumulation. The most likely reason for these results to become inaccurate is when future changes in the large-scale atmospheric circulation and its effects on snowfall distribution are not well represented17. We also note that meltwater ponding does not necessarily imply ice shelf break-up through hydrofracturing, because hydrofracture may not always occur8,29 or the ice shelf may be able to sustain some amount of hydrofracture25.
Nonetheless, it is evident that numerous cold and dry Antarctic ice shelves are more susceptible to meltwater ponding than previously thought. Further refining these results will require improved (satellite) observations of melt ponding and Earth system models with improved snow physics and/or polar-specific, high-resolution regional climate models.
Methods
Regional atmospheric climate model
We used the hydrostatic regional atmospheric climate model RACMO2.3p2 over Antarctica3. At the lateral and ocean boundaries, the model is forced by ERA5 reanalysis30 data every six hours from 1979 to 2021. The model is run at 27 km horizontal resolution for the entire AIS (henceforth R-ERA5), which constitutes an update of the simulation forced from 1979 to 2018 by ERA-Interim31 reported in ref. 3. Upper air relaxation is also active32. The model topography and ice mask in this model are aggregated from ref. 33 and from ref. 34 for the AP. The data used in this study are provided in ref. 35.
CESM2
To simulate the recent past (1950–2014) and the future (2015–2100), we used RACMO2.3p2 at 27 km resolution to dynamically downscale one historical and three future projections emission scenarios (SSP1-2.6, SSP2-4.5 and SSP5-8.5) of CMIP6, henceforth called R-HIST and R-CESM2 (SSP126, SSP245 and SSP585). CESM2 simulates coupled interactions between atmosphere–ocean–land systems on the global scale. The model incorporates the Community Atmosphere Model version 6 (ref. 36), the Parallel Ocean Program model version 2.1 (ref. 37) and the Los Alamos National Laboratory Sea Ice Model version 5.1 (ref. 38). Here we used a full atmosphere–ocean coupling in CESM2—that is, including sea ice dynamics and sea surface temperature evolution while excluding land ice dynamics (for example, calving). The model is run at 1° (~100 km) spatial resolution and only prescribes atmospheric greenhouse gas (CO2 and CH4) and aerosol emissions as well as land cover use39. A detailed model description, the latest updates40 and an evaluation over Greenland are provided in ref. 41.
Fitting MOA
Using the five climate simulations at 27 km for the AIS, we fit exponential and power-law relations of annual total liquid water production (melt + rain; M) and snow accumulation (snowfall − sublimation; A) to calculate MOA sensitivity as a function of annual average T2m:
where a, b, c and d are fitting parameters. This approach enabled us to solve for T2m for MOA = 0.7 and compare this threshold temperature (TT) with modelled warming rates in different climate projections and models. To calculate the uncertainty, dTT, we used the error (one standard deviation) in both fits (for example, a ± da) to calculate a lower and upper value of the temperature intersection TT. Our calculations were done by first averaging ice shelf annual melt and accumulation and then calculating TT ± dTT (Figs. 1, 2 and 4; Extended Data Fig. 1; and Supplementary Fig. 3), but we also calculated TT and dTT for every grid point separately (Fig. 3 and Extended Data Fig. 2). For some ice shelves and grid points, TT has already been passed, or annual snow accumulation is negative (sublimation > snowfall). Here we conservatively replace TT by using average present-day T2m with a dTT of 10%. The code is provided in ref. 42.
Sentinel-2 observed melt volumes
To assess the performance of the ΔT < 0 threshold, we compared it with meltwater lake volume observations from the Sentinel-2 satellite record over the austral summers of 2015–2022. We applied the method for lake detection/volume of ref. 43 to first detect lake presence on the basis of thresholds for different satellite indices (that is, normalized difference water index, normalized difference snow index, and different and individual reflectance). Next, the detected lake pixels were converted to lake depths on the basis of a physically based model that relates reflectance to depth on the basis of the premise that light passing through a water column is attenuated with depth, due to absorption and scattering processes. This method of ref. 43 was applied to 19,213 Sentinel-2 Level-1C top-of-atmosphere reflectance granules with less than 30% cloud cover and solar elevation angles above 25 degrees over all Antarctic ice shelves and the surrounding ice sheet. The resulting melt pond volume datasets were then aggregated on the 27 km RACMO2.3p2 grid, accumulating the melt ponds that fell within one model grid cell (Extended Data Fig. 3). We furthermore compared our results with melt pond products of refs. 26,28 in Supplementary Fig. 2b. The data used in this study are provided in ref. 35.
CMIP6 data
We obtained CMIP6 data from the KNMI Climate Explorer at https://climexp.knmi.nl/start.cgi. We used member average annual average (2090–2100) surface air temperature from all available models for warming scenarios SSP1-2.6 (40 models), SSP2-4.5 (40 models), SSP3-7.0 (36 models) and SSP5-8.5 (41 models). The Climate Explorer was used to directly mask output over the specific ice shelves in our study, chosen to be large enough to be represented by the coarse grids of the CMIP6 models. Box plots were then constructed for each ice shelf and each scenario, showing the 90%, 33% and median percentiles of the ensemble.
Data availability
The data used in this study are obtainable at https://doi.org/10.5281/zenodo.7334047 (ref. 35). The CMIP6 data were obtained from the KNMI Climate Explorer at https://climexp.knmi.nl/start.cgi. The Sentinel-2 melt pond volumes aggregated on the model grid are based on lake depths per pixel that are available as a public Google Earth Engine collection on https://code.earthengine.google.com/?asset=projects/ee-earthmapps/assets/S2_LakesAntarctica_v3.
Code availability
The Python code for calculating the temperature threshold is obtainable at https://doi.org/10.5281/zenodo.7346880 (ref. 42). The figures were generated in NCL, and the figure code can be obtained from the authors upon request and without conditions.
References
Lhermitte, S. et al. Damage accelerates ice shelf instability and mass loss in Amundsen Sea Embayment. Proc. Natl Acad. Sci. USA 117, 24735–24741 (2020).
Trusel, L. D., Frey, K. E., Das, S. B., Kuipers Munneke, P. & van den Broeke, M. R. Satellite-based estimates of Antarctic surface meltwater fluxes. Geophys. Res. Lett. 40, 1–6 (2013).
Van Wessem, J. M. et al. Modelling the climate and surface mass balance of polar ice sheets using RACMO2, part 2: Antarctica (1979–2016). Cryosphere 2018, 1479–1498 (2018).
Bell, R. E., Banwell, A. F., Trusel, L. D. & Kingslake, J. Antarctic surface hydrology and impacts on ice-sheet mass balance. Nat. Clim. Change https://doi.org/10.1038/s41558-018-0326-3 (2018).
Kuipers Munneke, P., Ligtenberg, S. R. M., Van Den Broeke, M. R. & Vaughan, D. G. Firn air depletion as a precursor of Antarctic ice-shelf collapse. J. Glaciol. 60, 205–214 (2014).
Fürst, J. J. et al. The safety band of Antarctic ice shelves. Nat. Clim. Change 6, 479–482 (2016).
Banwell, A. F., Willis, I. C., Macdonald, G. J., Goodsell, B. & MacAyeal, D. R. Direct measurements of ice-shelf flexure caused by surface meltwater ponding and drainage. Nat. Commun. 10, 730 (2019).
Lai, C. Y. et al. Vulnerability of Antarctica’s ice shelves to meltwater-driven fracture. Nature 584, 574–578 (2020).
Wille, J. D. et al. Intense atmospheric rivers can weaken ice shelf stability at the Antarctic Peninsula. Commun. Earth Environ. https://doi.org/10.1038/s43247-022-00422-9 (2022).
Rott, H. et al. Rapid collapse of northern Larsen Ice Shelf, Antarctica. Science 271, 788–792 (1996).
Cook, A. J. & Vaughan, D. G. Overview of areal changes of the ice shelves on the Antarctic Peninsula over the past 50 years. Cryosphere 4, 77–98 (2010).
Morris, E. M. & Vaughan, D. G. Spatial and temporal variation of surface temperature on the Antarctic Peninsula and the limit of viability of ice shelves. Antarct. Res. Ser. 79, 61–68 (2003).
Pfeffer, W. T., Meier, M. F. & Illangasekare, T. H. Retention of Greenland runoff by refreezing: implications for projected future sea level change. J. Geophys. Res. https://doi.org/10.1029/91jc02502 (1991).
Donat-Magnin, M. et al. Future surface mass balance and surface melt in the Amundsen sector of the West Antarctic Ice Sheet. Cryosphere 15, 571–593 (2021).
Palerme, C. et al. Evaluation of current and projected Antarctic precipitation in CMIP5 models. Clim. Dyn. 48, 225–239 (2017).
Van Wessem, J. M. et al. Improved representation of East Antarctic surface mass balance in a regional atmospheric climate model. J. Glaciol. 60, 761–770 (2014).
Beaumet, J., Déqué, M., Krinner, G., Agosta, C. & Alias, A. Effect of prescribed sea surface conditions on the modern and future Antarctic surface climate simulated by the ARPEGE atmosphere general circulation model. Cryosphere 13, 3023–3043 (2019).
Bracegirdle, T. J. et al. Twenty first century changes in Antarctic and Southern Ocean surface climate in CMIP6. Atmos. Sci. Lett. 21, 1–14 (2020).
Trusel, L. D. et al. Divergent trajectories of Antarctic surface melt under two twenty-first-century climate scenarios. Nat. Geosci. 8, 927–932 (2015).
Jakobs, C. L. et al. Quantifying the snowmelt-albedo feedback at Neumayer Station, East Antarctica. Cryosphere 13, 1473–1485 (2019).
Lenaerts, J. T. M. et al. Meltwater produced by wind–albedo interaction stored in an East Antarctic ice shelf. Nat. Clim. Change 7, 58–62 (2016).
Vignon, É., Roussel, M.-L., Gorodetskaya, I. V., Genthon, C. & Berne, A. Present and future of rainfall in Antarctica. Geophys. Res. Lett. 48, e2020GL092281 (2021).
Van Tricht, K., Lhermitte, S., Gorodetskaya, I. V. & van Lipzig, N. P. M. Improving satellite-retrieved surface radiative fluxes in polar regions using a smart sampling approach. Cryosphere 10, 2379–2397 (2016).
Tuckett, P. et al. Automated mapping of the seasonal evolution of surface meltwater and its links to climate on the Amery Ice Shelf, Antarctica. Cryosphere https://doi.org/10.5194/tc-2021-177 (2021).
Trusel, L. D., Pan, Z. & Moussavi, M. Repeated tidally induced hydrofracture of a supraglacial lake at the Amery Ice Shelf grounding zone. Geophys. Res. Lett. https://doi.org/10.1029/2021GL095661 (2022).
Stokes, C. R., Sanderson, J. E., Miles, B. W. J., Jamieson, S. S. R. & Leeson, A. A. Widespread distribution of supraglacial lakes around the margin of the East Antarctic Ice Sheet. Sci. Rep. 9, 13823 (2019).
Arthur, J. F. et al. The triggers of the disaggregation of Voyeykov Ice Shelf (2007), Wilkes Land, East Antarctica, and its subsequent evolution. J. Glaciol. 67, 933–951 (2021).
Corr, D., Leeson, A., Mcmillan, M., Zhang, C. & Barnes, T. An inventory of supraglacial lakes and channels across the West Antarctic Ice Sheet. Earth Syst. Sci. Data 14, 209–228 (2022).
Kingslake, J., Ely, J. C., Das, I. & Bell, R. E. Widespread movement of meltwater onto and across Antarctic ice shelves. Nature 544, 349–352 (2017).
Hersbach, H. et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049 (2020).
Dee, D. P. et al. The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 137, 553–597 (2011).
Van de Berg, W. J. & Medley, B. Brief communication: upper-air relaxation in RACMO2 significantly improves modelled interannual surface mass balance variability in Antarctica. Cryosphere 10, 459–463 (2016).
Bamber, J. & Gomez-Dans, J. A new 1 km digital elevation model of the Antarctic derived from combined satellite radar and laser data—part 1: data and methods. Cryosphere 3, 101–111 (2009).
Cook, A. J., Vaughan, D. G., Luckman, A. J. & Murray, T. A new Antarctic Peninsula glacier basin inventory and observed area changes since the 1940s. Antarct. Sci. 26, 614–624 (2014).
van Wessem, J. M., van den Broeke, M. R., Wouters, B. & Lhermitte, S. Data set: yearly RACMO2.3p2 variables, threshold temperature and Sentinel-2 melt pond volume. Zenodo https://doi.org/10.5281/zenodo.7334047 (2022).
Gettelman, A. et al. High climate sensitivity in the Community Earth System Model Version 2 (CESM2). Geophys. Res. Lett. 46, 8329–8337 (2019).
Smith, R. et al. The Parallel Ocean Program (POP) reference manual: ocean component of the Community Climate System Model (CCSM) and Community Earth System Model (CESM). Report LAUR-01853 (2010).
Bailey, D. et al. CESM CICE5 Users Guide (National Center for Atmospheric Research, 2018).
Eyring, V. et al. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958 (2016).
Danabasoglu, G. et al. The Community Earth System Model Version 2 (CESM2). J. Adv. Model. Earth Syst. 12, 1–35 (2020).
van Kampenhout, L. et al. Present-day Greenland ice sheet climate and surface mass balance in CESM2. J. Geophys. Res. Earth Surf. 125, 1–25 (2020).
van Wessem, J. M. Temperature thresholds. Zenodo https://doi.org/10.5281/zenodo.7346880 (2022).
Moussavi, M. S. et al. Antarctic supraglacial lake detection using Landsat 8 and Sentinel-2 imagery: towards continental generation of lake volumes. Remote Sens. 12, 1–19 (2020).
Acknowledgements
J.M.v.W. acknowledges support by PROTECT contribution number 53 and was funded by the Netherlands Organisation for Scientific Research (NWO) VENI grant no. VI.Veni.192.083. M.R.v.d.B. acknowledges support from the Netherlands Earth System Science Centre and PROTECT. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 869304, PROTECT contribution number 53. S.L. and B.W. were supported by grant no. OCENW.GROOT.2019.091 funded by NWO. We acknowledge L. van Kampenhout for providing the CESM2 forcing data.
Author information
Authors and Affiliations
Contributions
J.M.v.W. conceived the study, performed the model simulations and wrote the main manuscript with contributions from M.R.v.d.B., B.W. and S.L. S.L. provided the satellite data. All authors contributed to the interpretation of the results and commented on the manuscript and revisions.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Climate Change thanks Lauren Simkins and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Ice shelf average melt and accumulation fits.
Ice shelf averaged fits of yearly averaged melt and accumulation over all 56 major ice shelves > 800km2) by R-ERA5 (black), R-HIST (blue), R-126 (green), R-245 (yellow) and R-585 (red). R2 of both fits as well as a linear fit for accumulation (Alin) is denoted and the calculated temperature threshold TT and its uncertainty dTT. Ice shelves are ordered by their average present-day accumulation (note the different y-axis limits).
Extended Data Fig. 2 TT uncertainty.
Uncertainty (dTT) in the temperature threshold (TT), based on a lower and upper value of TT, calculated using the error (1σ) in the melt- and accumulation fits as described in the Methods section.
Extended Data Fig. 3 Sentinel-2 melt volumes.
Integrated 2015-2022 austral summer melt pond volume (m water equivalent) from Sentinel-2.
Supplementary information
Supplementary Information
Supplementary material including figures.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
van Wessem, J.M., van den Broeke, M.R., Wouters, B. et al. Variable temperature thresholds of melt pond formation on Antarctic ice shelves. Nat. Clim. Chang. 13, 161–166 (2023). https://doi.org/10.1038/s41558-022-01577-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41558-022-01577-1
This article is cited by
-
Geologically constrained 2-million-year-long simulations of Antarctic Ice Sheet retreat and expansion through the Pliocene
Nature Communications (2024)
-
Substantial contribution of slush to meltwater area across Antarctic ice shelves
Nature Geoscience (2024)
-
Antarctic-wide ice-shelf firn emulation reveals robust future firn air depletion signal for the Antarctic Peninsula
Communications Earth & Environment (2024)
-
Short- and long-term variability of the Antarctic and Greenland ice sheets
Nature Reviews Earth & Environment (2024)
-
Firn on ice sheets
Nature Reviews Earth & Environment (2024)