Abstract
Modelling of climate-driven range shifts commonly treats species as ecologically homogeneous units. However, many species show intraspecific variation of climatic niches and theory predicts that such variation may lead to counterintuitive eco-evolutionary dynamics. Here, we incorporate assumed intraspecific niche variation into a dynamic range model and explore possible consequences for six high-mountain plant species of the European Alps under scenarios of twenty-first century climate warming. At the species level, the results indicate massive range loss independent of intraspecific variation. At the intraspecific level, the model predicts a decrease in the frequency of warm-adapted haplotypes in five species. The latter effect is probably driven by a combination of leading-edge colonization and priority effects within the species’ elevational range and was weakest when leading-edge expansion was constrained by mountain topography The resulting maladaptation may additionally increase the risk that alpine plants face from shrinkage of their ranges in a warming climate.
Similar content being viewed by others
Main
Ongoing climate change will probably alter species’ ranges profoundly1. Many species are projected to face massive range loss or at least pronounced geographical redistribution of climatically suitable areas2,3,4. However, despite recent progress, predictive modelling of climate-driven range shifts still suffers from poor integration of relevant biological mechanisms such as dispersal, demography, species interactions or evolutionary responses of species to the changing climate5. Among the most widespread simplifications inherent to most modelling studies is the interpretation of climatic niches as traits characteristic of species as a whole. In fact, climatic tolerance is an attribute of individuals and the niche of the species is an abstraction resulting from the aggregation of individual specializations6,7,8. Under climate change, such intraspecific variation may have divergent effects on species’ range dynamics. On the one hand, individual specialization and local adaptation of populations probably decrease a species’ ability to persist at any given location as compared to model predictions which disregard such variation9,10,11,12,13. On the other hand, if niche position and size are determined genetically, haplotypes associated with adaptation to relatively warmer climatic conditions (further referred to as warm-adapted haplotypes) may already be present in colder environments due to gene flow. With warming they may increase in frequency and therefore buffer populations against the changes to come14,15,16,17. Finally, theory suggests that intraspecific variation in climatic niches may result in maladaptation of migrating populations under climate change as a consequence of leading-edge colonization and founder effects18,19,20. Evaluating the scale and impact of these processes on the response of species to twenty-first century climate warming requires models that integrate the inheritance of genetically determined individual niche variation with simulations of demographic and dispersal processes.
Here, we developed such a model by expanding the coupled niche–demographic modelling framework, 'cellular automaton-type tool for simulating plant spread' (CATS)21. CATS combines climatic niche modelling with stage-structured demographic simulations, mechanistic dispersal kernels and, as a new feature, a population genetic model. The model is discrete in space and time and operates on a geographical raster that represents variation in climatic (and other environmental) conditions in a study area. Across this study area, CATS projects how the size and geographical distribution of species populations change from year to year in response to changes of climatic conditions that alter vital rates such as germination, seed production and adult survival in individual raster cells. The new population genetic module assumes inheritable variation in climatic tolerances among individuals and simulates how climatic changes trigger changes in standing genetic composition and variability. We thereby presume that niches are coded by haplotypes that represent particular fractions of the entire species’ niche. To keep computational efforts within feasible limits, we simplify the likely complex genetic architecture of climatic specialization22 and assume that individual differences in climatic niches are determined by one diploid locus with up to ten alleles or up to three diploid diallelic loci. These few loci may be interpreted as those playing a key role in temperature adaptation by regulating the expression of downstream genes (for example, ref. 23). Each haplotype covers a variable fraction (ω = 50%, 75% or 100%) of the entire species’ niche breadth. The entire species’ niche breadth is derived from occurrence data of the species across the entire European Alps. As there is no empirical evidence on dominant–recessive heredity in genes related to climatic adaptation, we parsimoniously assume that allelic effects on an individual’s climatic optimum are purely additive; that is, that homozygosity does not have any deleterious effects. For more details on the modelling framework see Methods.
From the 150 species modelled in ref. 21, we selected six clearly diploid species occurring in alpine grasslands: Campanula pulla, Dianthus alpinus, Pedicularis rostratocapitata, Phyteuma hemisphaericum, Saponaria pumila and Silene acaulis ssp. exscapa. Half of these six species (C. pulla, D. alpinus and P.rostratocapitata) occur on calcareous substrate and half (P. hemisphaericum, S. pumila and S. acaulis) on siliceous substrate. Additionally, half of the species (P.rostratocapitata, P. hemisphaericum and S. acaulis) are widely distributed across the European Alps, while the other half are endemics of the Austrian part of the European Alps. We applied the model to simulate the range dynamics of these species across the entire European Alps until 2080 under two future IPCC Fifth Assessment Report (AR5) climate scenarios (representative concentration pathways RCP 2.6 and RCP 8.5). These scenarios reflect different greenhouse gas trajectories based on different socio-economic, political and technological assumptions for the twenty-first century. The RCP 2.6 scenario assumes that global annual greenhouse gas emissions (measured in CO2 equivalents) peak between 2010 and 2030 and decline substantially thereafter, while in the RCP 8.5 scenario, emissions continue to rise throughout the twenty-first century24. All six herbaceous species commonly occur above the alpine treeline and are hence among the species considered at particular risk under climate warming25,26. Using empirical distribution data from all across the Alpine arch we first fitted the niches of the entire species along three dimensions describing adaptation to temperature, water availability and soil properties. As information on real climatic specialization of individuals is not available for these or comparable alpine species, we then partitioned the temperature dimension of these three-dimensional niches into fractions assumed to cover half or three-quarters of the entire species' niche, respectively, and to be shifted along the temperature gradient to cover the species' whole temperature range (the number of resulting shifted niches is derived from the different numbers of assumed haplotypes; Methods). Although water availability and soil properties, such as calcium content, are important for alpine plants (for example, ref. 27), we here simplified the multidimensional nature of environmental adaptation and restricted intraspecific variation to the temperature gradient to facilitate interpretation of results. As a control, model runs included scenarios of neutral genetic variation; that is, where all individuals had the same niche as the species as a whole and hence did not differ in fitness along environmental gradients. All simulations started from the same initial distribution of species across the Alps. These initial distributions were constrained by actual mapped distributions of the species28, with standing genetic composition, that is, haplotype frequencies assumed to be in equilibrium with the environment as determined by a burn-in-simulation. Simulation runs then tracked the changes in the distribution of the species as a whole as well as in the frequency of haplotypes across the Alps triggered by climatic scenarios (Methods).
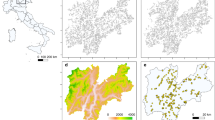
With respect to entire species ranges, our results corroborate previous predictions; for example, refs. 21,25,29, of moderate to massive range loss of alpine plants, especially under the more pronounced climate scenario (Fig. 1). Variation in the number of haplotypes did not change these results significantly (Table 1), probably because range loss predominantly occurs at trailing elevational range edges26,30 where no better-adapted haplotypes are available for replacement of those going locally extinct. However, predicted range loss marginally increased with narrower niches of haplotypes, maybe because narrower niches require faster movement to track a changing climate. More importantly, climate warming changed relative haplotype frequencies. In particular, pronounced warming (RCP 8.5) was associated with a slight decrease (S. acaulis ssp. exscapa and C. pulla, median of −10.3% and −15.1%, respectively) or pronounced decrease (P. rostratocapitata, P. hemisphaericum and S. pumila, median of −36.0%, −75.5% and −62.3%, respectively) in the relative frequency of the warm-adapted haplotype at the end of the simulation period (Fig. 2). By contrast, the frequency of the warm-adapted haplotype only increased (slightly) in one species, D. alpinus (median of 15.3%). Across all six species, the relative loss of warm-adapted haplotypes was stronger under more pronounced climate scenarios and with a higher number of different haplotypes but weaker when the niches of individual haplotypes were assumed to be narrower and for overlap among haplotype niches (and also potential distribution areas) to be less pronounced (Table 1).
Both values were calculated in proportion to the current range size of the species in the European Alps. They represent results from simulations under RCP 2.6 and RCP 8.5, averaged over two different settings of demographic and dispersal parameters representing upper and lower margins of plausible species mobility and, in case of range loss, over all different levels of intraspecific variation explored (Methods). Error bars depict standard deviation.
Boxplots represent changes in the European Alps under the mild RCP 2.6 and the pronounced RCP 8.5 climate scenarios. as well as on an artificial test grid under assumed intermediate and pronounced climate change (warming of 2 °C and 4 °C, respectively). Negative values, that is, those below the horizontal line, indicate a decrease in the frequency in the population.
To better understand the reasons for this decline of warm-adapted haplotypes, we additionally ran models on an artificial test grid, representing a mountain slope with homogeneous precipitation and soil conditions but a linear temperature decrease with elevation. We simulated range dynamics of species in this artificial landscape under different degrees of assumed temperature increase over the same time span (80 years). All parameters of the six species, their niches and their intraspecific variation were the same as in the real-world models (Methods). In these artificial landscapes, the reduction in the frequency of the warm-adapted haplotype was even more pronounced than in the real-world simulations (Fig. 2). Moreover, this reduction occurred consistently across all six species (Fig. 2), irrespective of all differences in niche positions, niche size, demographic and dispersal features among them.
The developing maladaptation (that is, the decreasing relative frequency of the warm-adapted haplotype under warming conditions) may be caused by priority effects and intraspecific competition. Individuals carrying the cold-adapted haplotype at the species’ leading edge can expand their range upslope into terrain hitherto uncolonized by the species. In contrast, individuals carrying cold-adapted haplotypes at the initially occupied sites block individuals carrying the warm-adapted one from succeeding upwards (Fig. 3 and Extended Data Figs. 1–5). This blocking effect is driven by two factors: first, the long life spans of alpine plants31 which limit the rate at which new recruits can establish; and, second, the fact that the locally prevailing haplotype predominates in the cohort of new recruits because it produces more clonal offspring and a higher number of seeds (most of which is distributed over <10 m in alpine herbs32). The reason why the decrease in the warm-adapted haplotype was consistent across all species on the artificial mountain slope but emerged only in part of the species in the real-world simulation may relate to mountain topography. While the artificial slope was designed to offer unrestricted opportunities of upslope movement, real-world mountain tops set upper limits to species migration. To assess the possible effect of topography on our simulation results we calculated the upslope area reachable for the species (that is, within a radius of 1 km of occupied sites) at the end of the simulation period. We found that D. alpinus and S. acaulis ssp. exscapa were the two species with most pronounced total range loss and smallest remaining upslope area (Fig. 1). These are, at the same time, the two species in which the decrease of the warm-adapted haplotype was least pronounced (S. acaulis ssp. exscapa) or this haplotype even increased in frequency (D. alpinus). A relative decrease of warm-adapted haplotypes may thus not occur or play a minor role in species with limited opportunity of leading-edge expansion but at the cost of nowhere-to-go situations for cold-adapted haplotypes.
a–c, Elevational distribution of haplotypes at the beginning (a) and end (c) of the simulation as well as the overall frequency change during the simulation period (b). Colours indicate warm-adapted (red) to cold-adapted (blue) haplotypes. Simulations assumed an increase in temperature of 4 C° over 80 yr. The niche of each of the five different haplotypes comprised 75% of the species’ niche breadth and was determined by one diploid locus (compare Extended Data Fig. 6). As temperature increases, the population shifts upslope (to the left) but the warm-adapted haplotype (red) is blocked by intraspecific competition. As a result, the proportion of individuals carrying the cold-adapted haplotype increases with warming.
The disproportionate loss of warm-adapted haplotypes under climate warming appears counterintuitive, at first glance. Our results are, however, in line with the importance of density-dependent processes for the emergence of biogeographical patterns in the past19 and with theoretical simulations of climate-driven range shifts of ecologically structured populations18. Here, we show that models run in a real-world topography with niches, demographic and dispersal rates fit from empirical data may lead to similar conclusions. On the other hand, we also demonstrate that the structure of real landscapes can modify or even reverse the future development of the standing genetic composition. Generalizations of how climate change will affect intraspecific diversity of high-mountain plants appear difficult.
Despite its complexity, our model still necessarily oversimplifies reality. Simplifications related to the CATS model in general have already been discussed elsewhere (for example, refs. 21,33,34) and include coarse estimates of yet purely quantified demographic parameters as well as neglect of factors such as microclimatic variation in alpine terrain35 or extreme climatic events36. Here, we specifically note that our simulations accounted for intraspecific but not for interspecific interactions. In reality, leading-edge colonization of cold-adapted haplotypes, which appears unrestricted by interactions in our model, may be hampered by competition with other species, either resident ones or those migrating upslope simultaneously. However, interspecific interactions are not limited to the leading edge of species, their competitive effect often decreases with elevation and species from lower elevations are, by trend, competitively superior to those from higher elevations37,38. For this reason, we tentatively assume that including interspecific interactions into the model may result in even more pronounced species range loss but that effects on the relative frequency of haplotypes would be qualitatively similar. We additionally emphasize that the population genetic module accounts for adaptation from standing genetic diversity only and disregards mutations. In reality, populations will most likely adapt to new environments in both ways, selection on pre-existing genetic variation as well as selection on new mutations39. Among those, adaptation from standing genetic variation is likely to work faster as, for example, beneficial haplotypes already start at higher frequencies. Over the upcoming decades of rapid climate warming, disregarding mutation appears arguable, particularly in slow life-cycle species like alpine plants. However, over longer time scales and after climate has reached a new equilibrium, mutations may play a role in diminishing the resistance of resident haplotypes against those better-adapted to the warming conditions12,40.
In reality, the genetic mechanisms controlling thermal tolerances of individuals are probably complex and certainly much more complicated than represented in our model41. Whether the implicit simplification of polygenic inheritance to one multiallelic or up to three diallelic loci may affect our results is not straightforward. However, sensitivity analyses of the two- and three-loci simulations at least suggest that our conclusions are robust against increasing recombination rates that may occur when a higher number of loci contribute to determining the thermal niche. Moreover, the general phenomenon of high-density blocking is well-documented in nature, for example, in colonization of deglaciated regions, where rapid expansions often lead to high genetic homogeneity19. Whether these examples include cases where secondary dispersers were better-adapted to changing conditions than were residents is unknown. In general, it seems plausible, however, that resident populations represent a barrier for newcomers which may gradually decrease in effectiveness with increasing difference in adaptation to the locally prevailing conditions.
Many unknowns remain when modelling range responses of species to climate change. Among them, our simulations emphasize that individual variation in climatic niches and intraspecific blocking are hitherto neglected but potentially important aspects. Whether these processes improve species’ prospects or change them for the worse appears subject to a complex interplay between the actual differentiation of the species’ niche space, the strength of biotic interactions among individuals and the spatial structure of environmental conditions in real landscapes. Incorporating these factors into eco-evolutionary models of species’ response to climate change requires foremost a better understanding of the genomic basis of local adaptation to heterogeneous climates23. For alpine plants, the results achieved here suggest that at least in part of the species those haplotypes pre-adapted to the climate to come may also be those suffering most from the altered conditions, at least over a possibly extended phase of transition42. As a corollary, high-mountain floras might be even more vulnerable to climate warming than so far predicted. These findings emphasize the call for expanding area-based conservation efforts43 also in mountain environments as protection from additional pressures such as intense agricultural use, energy production or resource extraction might facilitate population persistence during transient phases of maladaptation.
Methods
Study area
All simulations were run at a 100 × 100 m resolution for the entire European Alps, which cover ~200,000 km². Elevations reach 4,810 m above sea level at the highest peak (Mont Blanc, elevational data were obtained from ref. 44). Mean annual temperature ranges from approximately −13 up to 16 °C and annual precipitation sums reach up to ~3,600 mm (climatic conditions were obtained from WorldClim45).
Species data
True presences/absences were derived from complete species lists of 14,040 localized plots covering subalpine and alpine non-forest vegetation of the Alps, compiled from published46 and unpublished data sources. For more information see the supplementary information in ref. 21.
Data on demographic rates as well as dispersal parameters were taken from ref. 21, Supplementary Table 1. Detailed values are provided in Supplementary Table 1.
Environmental variables
Current climate data
Maps of current climatic conditions were generated on the basis of mean, minimum and maximum monthly temperature obtained from WorldClim45 and monthly precipitation sums derived from ref. 47 at a resolutions of 0.5 arcmin and 5 km, respectively. Temperature and precipitation data were downscaled to 100 m as described in ref. 21 and using ordinary kriging with elevation as covariable. As the reference periods of these two datasets do not match (temperature values represent averages for 1950–2000, while precipitation covers 1970–2005) temperature values were adapted using the E-OBS climate grids available online (www.ecad.eu/download/ensembles/download.php). We used these spatially refined temperature and precipitation grids to derive maps of mean annual temperature and mean annual precipitation sum. We chose only two climatic variables to keep models simple and, therefore, interpretation of results more straightforward. In fact, the climatic drivers of population performance and distribution can be more complex48 and vary among species, life history stages and vital rates49. However, as correlations between different descriptors of temperature (such as coldest month or warmest month temperature, Pearson correlation of 0.84) as well as between precipitation variables are high in the European Alps, we chose mean annual temperature and mean annual precipitation sum as they give the most basic description of how climatic conditions change over geographical and elevational gradients.
Future climate data
Monthly time series of mean temperature as well as precipitation sums predicted for the twenty-first century were extracted from the Cordex data portal (http://cordex.org). We chose two IPCC5 scenarios from the RCP families representing mild (RCP 2.6) and severe (RCP 8.5) climate change to consider the uncertainty in the future climate predictions. Both scenarios were generated by Météo-France/Centre National de Recherches Météorologiques using the CNRM-ALADIN53 model, fed by output from the global circulation model CNRM-CM5 (ref. 50). The RCP 2.6 scenario assumes that radiative forcing reaches nearly 3 W m−2 (equal to 490 ppm CO2 equivalent) mid-century and will decrease to 2.6 W m−2 by 2100. In the RCP 8.5 scenario, radiative forcing continues to rise throughout the twenty-first century and reaches >8.5 W m−2 (equal to 1,370 ppm CO2 equivalent) in 210024.
These time series were statistically downscaled (delta method) by (1) calculating differences (deltas) between monthly temperature and precipitation values hindcasted for the current climatic conditions (mean 1970–2005) and forecasted future values at the original spatial resolution of 11′; (2) spatially interpolating these differences to a resolution of 100 × 100 m using cubic splines and (3) adding them to the downscaled current climate data separately for each climatic variable21,36. Subsequently, we calculated running means (averaged over 35 years) for every tenth year (2030, 2040 through to 2080) for each climatic variable and finally derived, on the basis of the monthly data, mean annual temperature and mean annual precipitation sums for these decadal time steps. The application of 35-yr running means ensures that we use the same time interval for parameterization and prediction. Furthermore, for long-lived species such as alpine plants, running means over long time intervals appear most appropriate to characterize climatic niches33.
Soil data
In addition to the climatic data we used a map of the percentage of calcareous substrate within a cell (5′ longitude × 3′ latitude dissolved to 100 m resolution; further referred to as soil) as described in the supplementary information of ref. 21.
Environmental suitability modelling
We parameterized logistic regression models (LRMs) with a logit link function using species presence/absence data as response and the three environmental (two bioclimatic and one soil) variables as predictors. All predictor variables entered the model as second-order polynomials in agreement with the standard unimodal niche concept.
From the models, we also derived a threshold value to use for translating predicted probability of occurrence (as a measure of site suitability) into predicted presence or absence of each species at a site (called occurrence threshold, OT, henceforth). The threshold was defined such that it optimized the true skills statistic (TSS), a measure of predictive accuracy derived from comparing observed and predicted presence–absence maps51.
Genetic model and niche partitioning
Species-specific suitability curves for the annual mean temperature gradient derived from the LRMs were partitioned into suitability curves of ecologically different haplotypes of a species as defined by allelic variation in up to three diploid loci (Extended Data Fig. 6). The number of alleles was varied (n = 1, 2, 3, 5 and 10 alleles) as was the proportion of the entire species' (temperature) niche covered by each haplotype. Models with more than one locus were run with diallelic loci, as otherwise computational efforts would have increased excessively (for each haplotype the number of seeds, juveniles and adults has to be stored and all seeds have to be distributed separately). Each combination of haplotype number and allelic niche size used in a particular simulation is further referred to as setting. Species-specific suitability curves along the other two dimensions (precipitation and soil) remained unpartitioned to ease interpretation of results. The implications of relaxing this assumption by modelling niche partitioning along different environmental gradients are hard to predict. Outcomes would probably depend on the direction and strength of individual specialization along these gradients, whether they are positively or negatively correlated, as well as on how both temperature and precipitation patterns will be affected by climate change. As a consequence, the patterns we found could be re-enforced, for example when the replacement of cold-adapted haplotypes within the species elevational range is further delayed, for example, because those haplotypes adapted to warmer conditions can cope less well with higher precipitation at higher elevations. Vice versa, maladaptation to the warming temperatures might be attenuated, for example, if temperature increase is paralleled by precipitation decrease and emerging drought stress. If, in this case, haplotypes from lower elevations can better cope with both higher temperatures and less water availability than those of median elevations, they may replace the latter faster at these median elevations and hence shorten the phase of maladaptation.
Allelic effects were assumed to define the temperature optimum additively. Hence, the heterozygotes’ optimum is always exactly between the optima of the two corresponding homozygotes, corresponding to a codominant genetic model. Finally, all haplotypes corresponding to one setting were assumed to have constant (temperature) niche size, defined as a proportion (ω = 50%, 75% and 100%, for one haplotype only 100%) of the entire species’ (temperature) niche. The temperature niche was computed as the difference between the upper and lower temperature values at which the LRM-derived suitability curve predicted a suitability equal to OT (with precipitation and soil set to the respective optima of the species, also derived from the LRMs). To derive the same geographic distribution under current climatic conditions for each setting, the union of the niches of all haplotypes of one set has to approximate the niche of the single-species model (Extended Data Fig. 6). Note, however, that, the aspired equality of niches is impossible, as the niches resulting from a logistic regression with quadratic terms are always elliptic in shape. Therefore, the optima of the two extreme homozygotes (that is, those carrying haplotypes adapted to the coldest or warmest margins of the entire species' niche) are fixed at: niche limits ± 1/2 × ω × niche size and all other optima are distributed between them at equal distances (Extended Data Fig. 6 gives a schematic illustration). As a consequence, the performance of the extreme haplotypes, both coldest and warmest, is modelled to be somewhat higher towards the cold and warm margins of the temperature niche, respectively, compared with the performance modelled for the species without intraspecific niche partitioning (compare the overlap of the black with the red and blue curves in Extended Data Fig. 6a). However, as haplotype number did not affect modelled range loss (compare Table 1), this marginal mismatch does not apparently impact our results. Homozygotes were ordered from the cold-adapted A1A1 up to the warm-adapted AnAn.
Finally, the suitability curves of the genotypes were assumed to have the same value at their optimum as the species-specific suitability curve at this point (Extended Data Fig. 6).
Artificial landscapes
Artificial landscapes were defined as a raster of 50 × 112 cells (of 100 × 100 m). These rasters were homogeneous with respect to precipitation and soil carbon conditions which were set to the values optimal for each species according to the LRMs. With respect to temperature, by contrast, we implemented a gradient across the raster running from the minimum –9.1 °C to the maximum +3.8 °C temperature for which the LRM predicts values >OT across all six species. Buffering by 1 °C at both limits was done to avoid truncating simulation results. Further 4 °C at the lower limit were added to consider simulated temperature increase (below). The final temperature range represented by the raster ran from −14.1 to +4.8 °C. Temperature increased linearly along this axis by an increment of 0.171 °C per cell, derived from a 20° slope and a temperature decrease of 0.5 °C per 100 m of elevational change. Along the 50-cell breadth of the landscape, temperature values were kept constant. On the basis of these grids, we implemented a moderate and a severe climate change scenario, characterized by temperature increases of 2 and 4 °C, respectively, over 80 yr. Therefore, temperature of each raster cell increased annually by 0.025 and 0.05 °C, respectively.
Simulations of spatiotemporal range dynamics
CATS21 is a spatially and temporarily explicit model operating on a two-dimensional grid (of 100 m mesh size in this case). CATS combines simulations of local species' demography with species' distribution models by scaling demographic rates relative to occurrence probabilities (suitabilities) predicted for the respective site or grid cell by the latter. Dispersal among grid cells is modelled as a combination of wind, exozoochoric and endozoochoric (that is, animal dispersal via attachment to the fur or ingestion and defecation, respectively) dispersal of plant seeds. Time proceeds in annual steps. The annually changing occurrence probabilities at each site affect the demography of local populations and hence, eventually, the number of seeds that are produced in each grid cell in the respective year. As a consequence, local populations grow or decrease, become extinct or establish anew and hence the species’ distribution across the whole study area changes as a function of the changing climate.
Demographic modelling
Climate-dependence of local demography was modelled by linking demographic rates (seed persistence, germination, survival, flowering frequency, seed yield and clonal reproduction) and carrying capacity to occurrence probabilities predicted by LRMs by means of sigmoidal functions. Furthermore, all rates were fixed at OT at a value ensuring stable population sizes; for more information see refs. 21,33. Demographic rates were confined by zero and a species-specific maximum value (Supplementary Table 1), which was assumed to be the same for all genotypes of a species. As a corollary, the demographic rates of all genotypes of a species are the same under optimal environmental conditions but their actual values for a particular site in a particular year differ due to different temperature optima of genotypes. In addition, germination, survival and clonal reproduction were modelled as density-dependent processes to account for intraspecific competition between genotypes. In our application, for all density-dependent functions, the species abundance is defined as the sum of all adult individuals in a given cell, regardless of their genotypes. Density dependence is commonly achieved by multiplying rates with (C – N)/C, where N is the species abundance and C is the (site- and genotype-specific) carrying capacity. This correction for density dependence causes the functions to drop to zero when N approximates C. To avoid the subsequent collapse of population sizes, we defined density-dependent rates as (C – N)/C × rate() + N/C × rate(OT), which ensures stable population sizes at densely populated sites occupied by only one genotype. To account for uncertainty in parameters of demographic rates, we assigned each species two value sets representing the upper and lower end of a plausible range of values on the basis of information derived from databases and own measurements (Supplementary Table 1).
The simulations allowed for cross-pollination between genotypes. We used the relative amount of flowers (genotype-specific flowering frequency as defined by the sigmoid curve for the given suitability in the given raster cell for the given year × number of adults of that genotype in the population of that cell) to derive an estimate of the haplotype frequencies in the total pollen produced by the population within a grid cell. For the multiallelic case we allowed for recombination between loci with a recombination rate of 0.1%. These frequencies were set equal to the probability that particular haplotypes are transmitted to each year’s seed yield by pollination. Spatial pollen dispersal was accounted for in the following way: in each cell, 5% of the pollen involved in producing the annual seed yield, was assumed to stem from outside the respective raster cell. The proportions of different haplotypes in this 5% were derived from the overall pollen frequencies in all cells within a 700 m radius around the target cell (following estimates in ref. 52). Subsequently, produced seeds of each genotype were divided into resulting genotypes regarding the adult’s haplotype composition and the haplotype frequencies in the cells' entire pollen load.
Dispersal modelling
For wind dispersal of plant species we parameterized the analytical WALD kernel53 on the basis of measured seed traits and wind speed data from a meteorological station in the Central Alps of Austria. Exozoochorous and endozoochorous plant kernels were parameterized on the basis of correlated random walk simulations for the most frequent mammal dispersal vector in the study area, the chamois (Rupicapra rupicapra L.). For more details, see ref. 33. To account for uncertainties in species-specific dispersal rates, the proportion of seeds dispersed by the more far-reaching zoochorous kernels was assumed either as high (1–5%) or low (0.1–0.5%), setting upper and lower boundaries of a credible range of the dispersal ability of species.
Simulation set up and simulation initialization
To test for the effects of climate change on genetic diversity in 2080, we ran CATS over the period 2000 to 2080 for each of the six study species across the entire Alps under a full factorial combination of (1) three niche sizes (50%, 75% and 100%); (2) six numbers of haplotypes (equal to two, three, five and ten alleles for one locus and four and eight for the diallelic two- and three-locus models, respectively); (3) three climate scenarios (current climate, RCP 2.6 and RCP 8.5); and (4) two sets of demographic and dispersal parameters. As a ‘control’ we also ran simulations for all climate scenarios and the two demographic and dispersal parameter sets for a setting with one genotype filling the whole niche of the species. To account for stochastic elements in CATS four replications were run for each combination of ‘treatments’.
For simulations in artificial landscapes we used, instead of RCP 2.6 and RCP 8.5, ‘artificial’ climatic scenarios with an assumed warming of 2 and 4 °C, respectively, and no change in precipitation.
All simulation runs were started with homozygotic individuals only. As initial distribution, for each simulation run each cell predicted to be environmentally suitable to the species (that is, occurrence probability of species >OT)—and within the real distribution range of the species28 (not relevant for simulations in artificial landscapes, of course)—was assumed to be occupied by an equal number of adults of each (homozygotic) genotype, with the total sum equal to the carrying capacity of the site. To accommodate this arbitrary within-cell genetic mixture of homozygotes (and missing heterozygotes) to actual local conditions we started simulations of range dynamics with a burn-in phase of 200 yr, run under constant current climatic conditions. To have a smooth transition from the burn-in phase under current climate (corresponding to the climate of the years 1970–2005; see current climate data) to future climate projections (starting with 2030) and to derive annual climate series, climate data were linearly interpolated between these two time intervals.
Statistical analysis
We evaluated the contribution of climate scenario, haplotype number and haplotype niche size to overall species’ range change as well as the change in the frequency of the warm-adapted haplotype by means of linear models. In these models, log(range size in 2080/range size in 2000) and log(percentage of warm-adapted haplotype in 2080/percentage of warm-adapted haplotype in 2000), averaged over the four replicates and the two demographic and dispersal parameter sets, were the response variables. For the analysis of the change of the warm-adapted haplotype simulation settings with 100% niche size were ignored, as in this setting all haplotypes have the same temperature optimum (that is, neutral genetic variation). Approximate normality of residuals was confirmed by visual inspection.
As indicator of the ‘topographic opportunity’ remaining to the species in the real world we calculated the area colonizable at elevations higher than those already occupied at the end of the simulation period. We therefore drew a buffer of 1 km around each cell predicted to be occupied in 2080 and then summed the area within these buffers at a higher elevation than the focal, occupied cell. Overlapping buffer areas were only counted once. This calculation was done for simulations conducted with one full-niche genotype per species only.
Sensitivity analysis
We interpret the simulated relative decrease of warm-adapted haplotypes mainly as an effect of (1) the unrestricted expansion of cold-adapted haplotypes at the leading edge and (2) the resistance of the locally predominating haplotype that becomes increasingly maladapted with progressive climate warming, to recruitment by better-adapted haplotypes from below that are either rare or not present at all initially. However, the results achieved, and our conclusions, may be sensitive to assumptions about particular parameter values. Parameters that control the longevity of adult plants, and indirectly the rate of recruitment of new individuals, as well as those controlling gene flow via pollen (instead of seeds) may be particularly influential in this respect. We additionally ran simulations on artificial landscapes under alternative values of these parameters. In particular, we set the maximum age of plants to 10 yr instead of 100 yr and raised the proportion of locally produced pollen assumed to be transported up to 700 m to 10%. Both of these values are thus probably set to rather extreme levels: a maximum age of 10 yr is much shorter than the 30–50 yr assumed to be the standard age of (non-clonal) alpine plants31; and a cross-pollination rate between cells of 10% is high given that among the most important alpine pollinators only bumblebees are assumed to transport pollen >100 m regularly54,55. We add that we ran these additional simulations only in combination with the demographic species parameters set to high values because a short life span combined with low-level demographic parameters did not allow for stable populations of some species, even under current climatic conditions.
For individual species, adapting plant age and cross-pollination rate between cells (Extended Data Fig. 7), did change the magnitude of loss of the warm-adapted haplotype. Nevertheless, for all of them the warm-adapted haplotype still became rarer when climate warmed and this effect increased with the level of warming. We are confident that our conclusions are qualitatively insensitive to variation of these parameters within a realistic range.
Finally, in the simulations where we assumed a multilocus structure of the temperature niche, the recombination rate may also affect simulation results because it determines the rate by which new haplotypes can emerge. We also tested sensitivity of our simulations to doubling the recombination rate to 0.2%. Again, we found that a higher recombination rate had little qualitative effect on the results. Quantitatively, it resulted in a slightly pronounced relative decrease of the warmth-adapted haplotype in most species (Extended Data Fig. 8).
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data that support the findings of this study as well as the source data are available online in the Phaidra database at https://phaidra.univie.ac.at/o:1376676, https://phaidra.univie.ac.at/o:1376677, https://phaidra.univie.ac.at/o:1376678, https://phaidra.univie.ac.at/o:1376679, https://phaidra.univie.ac.at/o:1376680 and https://phaidra.univie.ac.at/o:1376681.
Code availability
All code used for the simulation set up as well as analysis of results are available online in the Phaidra database at https://phaidra.univie.ac.at/o:1376682. Code for simulations (CATS code) is available from the corresponding author on request.
References
Bellard, C., Bertelsmeier, C., Leadley, P. W., Thuiller, W. & Courchamp, F. Impacts of climate change on the future of biodiversity. Ecol. Lett. 15, 365–377 (2012).
Thomas, C. D. et al. Extinction risk from climate change. Nature 427, 145–148 (2004).
Thuiller, W., Lavorel, S., Araújo, M. B., Sykes, M. T. & Prentice, I. C. Climate change threats to plant diversity in Europe. Proc. Natl Acad. Sci. USA 102, 8245–8250 (2005).
Warren, R., Price, J., Graham, E., Forstenhaeusler, N. & VanDerWal, J. The projected effect on insects, vertebrates, and plants of limiting global warming to 1.5°C rather than 2°C. Science 360, 791–795 (2018).
Urban, M. C. et al. Improving the forecast for biodiversity under climate change. Science 353, aad8466 (2016).
Clark, J. S. et al. Individual‐scale variation, species‐scale differences: inference needed to understand diversity. Ecol. Lett. 14, 1273–1287 (2011).
Hereford, J. A quantitative survey of local adaptation and fitness trade-offs. Am. Nat. 173, 579–588 (2009).
Bolnick, D. I. et al. The ecology of individuals: incidence and implications of individual specialization. Am. Nat. 161, 1–28 (2002).
Angert, A. L., Sheth, S. N. & Paul, J. R. Incorporating population-level variation in thermal performance into predictions of geographic range shifts. Integr. Comp. Biol. 51, 733–750 (2011).
Ikeda, D. H. et al. Genetically informed ecological niche models improve climate change predictions. Glob. Change Biol. 23, 164–176 (2017).
Peñuelas, J. et al. Evidence of current impact of climate change on life: a walk from genes to the biosphere. Glob. Change Biol. 19, 2303–2338 (2013).
Cotto, O. et al. A dynamic eco-evolutionary model predicts slow response of alpine plants to climate warming. Nat. Commun. 8, 15399 (2017).
Razgour, O. et al. Considering adaptive genetic variation in climate change vulnerability assessment reduces species range loss projections. Proc. Natl Acad. Sci. USA 116, 10418–10423 (2019).
Aguilée, R., Raoul, G., Rousset, F. & Ronce, O. Pollen dispersal slows geographical range shift and accelerates ecological niche shift under climate change. Proc. Natl Acad. Sci. USA 113, E5741–E5748 (2016).
Barton, N. in Integrating Ecology and Evolution in a Spatial Context (eds Silvertown, J. & Antonovics, J.) 365–392 (Blackwell, 2001).
Alleaume‐Benharira, M., Pen, I. & Ronce, O. Geographical patterns of adaptation within a species’ range: interactions between drift and gene flow. J. Evol. Biol. 19, 203–215 (2006).
Polechová, J., Barton, N. & Marion, G. Species’ range: adaptation in space and time. Am. Nat. 174, E186–E204 (2009).
Atkins, K. & Travis, J. Local adaptation and the evolution of species’ ranges under climate change. J. Theor. Biol. 266, 449–457 (2010).
Waters, J. M., Fraser, C. I. & Hewitt, G. M. Founder takes all: density-dependent processes structure biodiversity. Trends Ecol. Evol. 28, 78–85 (2013).
McInerny, G., Turner, J., Wong, H., Travis, J. & Benton, T. How range shifts induced by climate change affect neutral evolution. Proc. R. Soc. B 276, 1527–1534 (2009).
Dullinger, S. et al. Extinction debt of high-mountain plants under twenty-first-century climate change. Nat. Clim. Change 2, 619–622 (2012).
Evans, L. M. et al. Population genomics of Populus trichocarpa identifies signatures of selection and adaptive trait associations. Nat. Genet. 46, 1089–1096 (2014).
Fitzpatrick, M. C. & Keller, S. R. Ecological genomics meets community‐level modelling of biodiversity: mapping the genomic landscape of current and future environmental adaptation. Ecol. Lett. 18, 1–16 (2015).
Moss, R. H. et al. The next generation of scenarios for climate change research and assessment. Nature 463, 747–756 (2010).
Engler, R. et al. 21st century climate change threatens mountain flora unequally across Europe. Glob. Change Biol. 17, 2330–2341 (2011).
Rumpf, S. B. et al. Range dynamics of mountain plants decrease with elevation. Proc. Natl Acad. Sci. USA 115, 1848–1853 (2018).
Leuschner, C. & Ellenberg, H. H. Vegetation Ecology of Central Europe (Springer International Publishing, 2010).
Aeschimann, D., Lauber, K., Moser, D. M. & Theurillat, J.-P. Flora alpina: ein Atlas sämtlicher 4500 Gefässpflanzen der Alpen (Haupt Verlag AG, 2004).
Semenchuk, P. et al. Future representation of species’ climatic niches in protected areas: a case study with Austrian endemics. Front. Ecol. Evol. https://doi.org/10.3389/fevo.2021.685753 (2021).
Wiens, J. J. Climate-related local extinctions are already widespread among plant and animal species. PLoS Biol. 14, e2001104 (2016).
Körner, C. in Alpine Plant Life Ch. 16, 1–7 (Springer, 2003).
Tackenberg, O. & Stöcklin, J. Wind dispersal of alpine plant species: a comparison with lowland species. J. Veg. Sci. 19, 109–118 (2008).
Hülber, K. et al. Uncertainty in predicting range dynamics of endemic alpine plants under climate warming. Glob. Change Biol. 22, 2608–2619 (2016).
Wessely, J. et al. Habitat-based conservation strategies cannot compensate for climate-change-induced range loss. Nat. Clim. Change 7, 823–827 (2017).
Scherrer, D. & Körner, C. Topographically controlled thermal‐habitat differentiation buffers alpine plant diversity against climate warming. J. Biogeogr. 38, 406–416 (2011).
Zimmermann, N. E. et al. Climatic extremes improve predictions of spatial patterns of tree species. Proc. Natl Acad. Sci. USA 106, 19723–19728 (2009).
Callaway, R. M. et al. Positive interactions among alpine plants increase with stress. Nature 417, 844–848 (2002).
Alexander, J. M., Diez, J. M. & Levine, J. M. Novel competitors shape species’ responses to climate change. Nature 525, 515–518 (2015).
Barrett, R. D. & Schluter, D. Adaptation from standing genetic variation. Trends Ecol. Evol. 23, 38–44 (2008).
Bush, A. et al. Incorporating evolutionary adaptation in species distribution modelling reduces projected vulnerability to climate change. Ecol. Lett. 19, 1468–1478 (2016).
Fournier-Level, A. et al. A map of local adaptation in Arabidopsis thaliana. Science 334, 86–89 (2011).
Cotto, O. et al. A dynamic eco-evolutionary model predicts slow response of alpine plants to climate warming. Nat. Commun. 8, 15399 (2017).
Watson, J. E. M. et al. Set a global target for ecosystems. Nature 578, 360–362 (2020).
Digital Elevation Model over Europe (EU-DEM) (EEA, 2015); https://www.eea.europa.eu/data-and-maps/data/eu-dem
Hijmans, R. J., Cameron, S. E., Parra, J. L., Jones, P. G. & Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 25, 1965–1978 (2005).
Willner, W., Berg, C. & Heiselmayer, P. Austrian vegetation database. Biodivers. Ecol. 4, 333 (2012).
Isotta, F. A. et al. The climate of daily precipitation in the Alps: development and analysis of a high‐resolution grid dataset from pan‐Alpine rain‐gauge data. Int. J. Climatol. 34, 1657–1675 (2014).
Körner, C. & Hiltbrunner, E. The 90 ways to describe plant temperature. Perspect. Plant Ecol. Evol. Syst. 30, 16–21 (2018).
Löffler, J. & Pape, R. Thermal niche predictors of alpine plant species. Ecology 101, e02891 (2020).
Tramblay, Y., Ruelland, D., Somot, S., Bouaicha, R. & Servat, E. High-resolution Med-CORDEX regional climate model simulations for hydrological impact studies: a first evaluation of the ALADIN-Climate model in Morocco. Hydrol. Earth Syst. Sci. 17, 3721–3739 (2013).
Allouche, O., Tsoar, A. & Kadmon, R. Assessing the accuracy of species distribution models: prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecol. 43, 1223–1232 (2006).
Van Rossum, F. Pollen dispersal and genetic variation in an early‐successional forest herb in a peri‐urban forest. Plant Biol. 11, 725–737 (2009).
Katul, G. G. et al. Mechanistic analytical models for long-distance seed dispersal by wind. Am. Nat. 166, 368–381 (2005).
Scheepens, J., Frei, E. S., Armbruster, G. F. & Stöcklin, J. Pollen dispersal and gene flow within and into a population of the alpine monocarpic plant Campanula thyrsoides. Ann. Bot. 110, 1479–1488 (2012).
Lefebvre, V., Villemant, C., Fontaine, C. & Daugeron, C. Altitudinal, temporal and trophic partitioning of flower-visitors in Alpine communities. Sci. Rep. 8, 4706 (2018).
Acknowledgements
The computational results presented have been achieved using the Vienna Scientific Cluster. Species pictograms were drawn by Michael Herzog. S.D. has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (ERC-Adv grand MICROCLIM, Grant Agreement No. 883669).
Author information
Authors and Affiliations
Contributions
S.D. and J.W. designed the study. G.K., D.M. and J.W. compiled climate data. A.G. and J.W. built the simulation tool and ran all simulations. K.H. and J.W. performed the analysis. S.D., F.G. and J.W. wrote the text with further input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review information
Nature Climate Change thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Frequency of haplotypes along an artificial mountain slope (= temperature gradient) for Dianthus alpinus.
Panels depict the elevational distribution of haplotypes at the beginning (a) and end (c) of the simulation as well as the overall frequency change during the simulation period (b). Colours indicate haplotypes associated with warm (red) to cold (blue) climatic conditions. Simulations assumed an increase in temperature of 4 C° over 80 years. The niche of each of the five different haplotypes comprised 75% of the species’ niche breadth and was determined by one diploid locus (cf. Extended Data Fig. 6).
Extended Data Fig. 2 Frequency of haplotypes along an artificial mountain slope (= temperature gradient) for P. rostratocapitata.
Panels depict the elevational distribution of haplotypes at the beginning (a) and end (c) of the simulation as well as the overall frequency change during the simulation period (b). Colours indicate haplotypes associated with warm (red) to cold (blue) climatic conditions. Simulations assumed an increase in temperature of 4 C° over 80 years. The niche of each of the five different haplotypes comprised 75% of the species’ niche breadth and was determined by one diploid locus (cf. Extended Data Fig. 6).
Extended Data Fig. 3 Frequency of haplotypes along an artificial mountain slope (= temperature gradient) for Phyteuma hemisphaericum.
Panels depict the elevational distribution of haplotypes at the beginning (a) and end (c) of the simulation as well as the overall frequency change during the simulation period (b). Colours indicate haplotypes associated with warm (red) to cold (blue) climatic conditions. Simulations assumed an increase in temperature of 4 C° over 80 years. The niche of each of the five different haplotypes comprised 75% of the species’ niche breadth and was determined by one diploid locus (cf. Extended Data Fig. 6).
Extended Data Fig. 4 Frequency of haplotypes along an artificial mountain slope (= temperature gradient) for Saponaria pumila.
Panels depict the elevational distribution of haplotypes at the beginning (a) and end (c) of the simulation as well as the overall frequency change during the simulation period (b). Colours indicate haplotypes associated with warm (red) to cold (blue) climatic conditions. Simulations assumed an increase in temperature of 4 C° over 80 years. The niche of each of the five different haplotypes comprised 75% of the species’ niche breadth and was determined by one diploid locus (cf. Extended Data Fig. 6).
Extended Data Fig. 5 Frequency of haplotypes along an artificial mountain slope (= temperature gradient) for Silene acaulis ssp. Exscapa.
Panels depict the elevational distribution of haplotypes at the beginning (a) and end (c) of the simulation as well as the overall frequency change during the simulation period (b). Colours indicate haplotypes associated with warm (red) to cold (blue) climatic conditions. Simulations assumed an increase in temperature of 4 C° over 80 years. The niche of each of the five different haplotypes comprised 75% of the species’ niche breadth and was determined by one diploid locus (cf. Extended Data Fig. 6).
Extended Data Fig. 6 Schematic depiction of the partitioning of a species´ niche.
Panel (a) shows the suitability curve for the species (black) and for the single genotypes (blue to red, indicating cold to warm adaptation) with a niche size of 50% and two alleles for one locus. The horizontal line shows the occurrence threshold, that is, the suitability value above which conditions are suitable, b) niche partitioning along the temperature axes for two alleles and niche size of 50%, c) two alleles and niche size of 75% and d) three alleles and niche size of 50%. Heterozygotes are depicted by dashed lines.
Extended Data Fig. 7 Sensitivity of results to assumed longevity and cross-pollination rate between cells.
Boxplots represent changes in the frequency of the haplotype associated with warm climatic conditions on an artificial test grid under intermediate and pronounced climate change (warming of 2 °C and 4 °C, respectively) for three different parameter settings: the original parameters used in the study (green), maximum age of individuals reduced to 10 years (orange) and an increased (doubled) cross-pollination rate between cells (blue).
Extended Data Fig. 8 Sensitivity of results to assumed recombination rate.
Boxplots represent changes in the frequency of the haplotype associated with warm climatic conditions on an artificial test grid under intermediate and pronounced climate change (warming of 2 °C and 4 °C, respectively) for two different parameter settings for the multilocus cases: the original parameters used in the study (green), and an increased (doubled) recombination rate (pink).
Supplementary information
Supplementary Information
Supplementary Table 1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wessely, J., Gattringer, A., Guillaume, F. et al. Climate warming may increase the frequency of cold-adapted haplotypes in alpine plants. Nat. Clim. Chang. 12, 77–82 (2022). https://doi.org/10.1038/s41558-021-01255-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41558-021-01255-8
This article is cited by
-
Monitoring of species’ genetic diversity in Europe varies greatly and overlooks potential climate change impacts
Nature Ecology & Evolution (2024)
-
Genome-environment associations along elevation gradients in two snowbed species of the North-Eastern Calcareous Alps
BMC Plant Biology (2023)
-
Uncertainty and risk of pruned distributional ranges induced by climate shifts for alpine species: a case study for 79 Kobresia species in China
Theoretical and Applied Climatology (2023)
-
Decline in the alpine landscape aesthetic value in a national park under climate change
Climatic Change (2022)