Abstract
The Paris agreement focused global climate mitigation policy on limiting global warming to 1.5 or 2 °C above pre-industrial levels. Consequently, projections of hazards and risk are increasingly framed in terms of global warming levels rather than emission scenarios. Here, we use a multimethod approach to describe changes in extreme sea levels driven by changes in mean sea level associated with a wide range of global warming levels, from 1.5 to 5 °C, and for a large number of locations, providing uniform coverage over most of the world’s coastlines. We estimate that by 2100 ~50% of the 7,000+ locations considered will experience the present-day 100-yr extreme-sea-level event at least once a year, even under 1.5 °C of warming, and often well before the end of the century. The tropics appear more sensitive than the Northern high latitudes, where some locations do not see this frequency change even for the highest global warming levels.
Similar content being viewed by others
Main
Extreme sea levels (ESLs)1 are triggered by the combination of storm surges, tides and waves. At vulnerable locations, high ESLs can constitute severe hazards, causing extensive damages to both human settlements and coastal ecosystems when natural and engineered defenses are overtopped or breached 2,3,4,5,6. Inevitably, increasing global temperatures will continue to cause global mean sea-level rise7. Even without the potential effects of climate change on waves and storm surge, sea-level rise alone is expected to lead to increases in coastal flooding and/or erosion8,9,10,11.
Several recent studies or assessments that address coastal flooding at the global scale have characterized future evolution of ESLs, particularly as driven by relative sea-level change (RSLC)1,12. Some of these adopted a scenario perspective, analysing projected changes under future emission trajectories for various time horizons3,5,13,14,15,16,17,18. Others have used idealized projections of RSLC11.
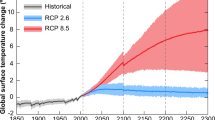
Only a few studies, some regional in scale, have characterized the effects of reaching alternative global warming levels (GWLs) independently of specific scenarios of future emissions19,20,21,22. These focused on the low end of the GWL range, in accordance with what motivated the Paris Agreement, that is, the measurable differential impacts for a world at 1.5 °C compared to one at 2 °C above pre-industrial levels23,24. Here, we take this GWL perspective but model RSLC for a wider range of values, from strong mitigation (1.5 °C) to high-end global warming (5 °C) and analyse consequences for ESL future frequencies. We note, however, that while the GWL framing is a natural fit for variables for which (at least on a century timescale) climatological changes with warming are largely time independent, for sea-level change the effects of different GWLs cannot be examined in a time-independent manner, as global mean sea level is more closely related to time-integrated temperature change than to the value of temperature at a given point in time25. Thus, sea level at a time when a given degree of warming is reached can be very different from sea level after the system has had time to equilibrate at that same warming level. We therefore also choose 2100 as a the time horizon by which different warming levels are achieved. We strongly emphasize epistemic uncertainty in the modelling of RSLC, using two methods for deriving its projections. One of them builds on aggregating existing results obtained by representative concentration pathway (RCP)-driven Earth System Model simulations according to their behaviour at 2100 (the GWL they reach, independently of the emission scenario followed, and not necessarily stabilizing at it, in most cases), using an ensemble of projections to account for uncertainties associated with parameters such as climate sensitivity, ocean heat uptake, glacier response and dynamic ocean response19. The second uses a simple model and combines information from Coupled Model Intercomparison Project Phase 5 (CMIP5) RCP-based projections of global temperature together with other IPCC-assessed and/or observationally constrained ranges of those same critical processes in its comprehensive uncertainty exploration26,27,28. We also include the effects of deeply uncertain factors contributing to ice-sheet changes29 for the 2 and 5 °C GWLs using results from a Structured Expert Judgment (SEJ) study30 (Methods).
For present-day ESLs at individual locations, our analysis also adopts a multimethod approach and gathers up to three estimates that used either observational records19 or hydrodynamic modelling16,17. The latter enables us to produce results for a large number of locations covering most of the world’s coastlines, and in one case16 also models the effects of tropical cyclones potentially making landfall at exposed locations. We pair the alternative estimates of current ESLs with the two alternative RSLC projections, producing six alternative fully probabilistic projections of future ESLs for a subset of 179 locations and four alternative projections at a larger set of 7,283 locations (when not using the observationally based current ESL estimates). We introduce a voting system, treating the alternative projections as individual experts and producing a central estimate, derived by asking for a majority vote, a lower—pessimistic—bound, akin to taking the most pessimistic projection, and an upper bound, which requires unanimity (Methods). The voting system yields a broad distribution comparable to that produced by ‘p-box’-based possibilistic approaches (for example, ref. 31) and would appear better suited at respecting the disparities in the alternative estimates we seek to merge. In addition, however, we compare the results of this synthesis approach to a more conventional full convolution of the four, or six, alternatives into a single distribution.
As in several previous studies10,14,19,32,33, future ESL changes are here taken to be solely a function of changes in mean sea level at a location, translating essentially into a uniform shift of the present-day ESL distribution. One of the methods considered here for the estimation of ESLs16 also modelled future changes in storm surge and waves but found that these contributions did not substantially affect the temporal dynamics of ESLs, especially at the global scale adopted herein, compared to the overwhelming effect of RSLC. Similarly, the focus on long-term changes and the global perspective made us choose not to address explicitly natural variability of ESLs, even if localized, mostly present-day analyses have shown its importance10,34. The expectation is that the size of RSLC will overwhelm such variability by the end of the century. Of course, even if limited by the length of the historical period used for estimating present-day ESLs (≥30 yr depending on the method), a portion of that internal variability is necessarily reflected in the ESL central estimates and their uncertainty bound.
Our focus here is on large-scale global assessment and we position our study as eminently relevant for scientists and policy-makers who are interested in the spatial dynamics of sea-level rise and its implications. Local stakeholders have to contend with additional uncertainties and components of impact risk, like exposure and vulnerability linked to topography and future socioeconomic conditions, for example. We do not address those here, as we focus our analysis on changes in a standard benchmark metric of hazards, the 100-yr ESL event (the extreme total water level expected to be experienced on average once in 100 yr or with 0.01 probability every year), recognizing that it may or may not be of immediate salience to individual localities.
GWLs triggering changes in frequency of ESLs
The study is framed to answer a specific question: what is the lowest warming level to trigger at least a 100-fold change in frequency of the present-day 100-yr ESL event, making it at least an annual occurrence by 2100?
We start from the subset of 179 locations at which we have six alternative estimates. For all components, RSLCs and ESLs, full probability distributions are available (Methods); in Supplementary Figs. 1–3 we show the three alternative mean estimates of the present-day 100-yr ESL and the associated standard deviations. Supplementary Figs. 4–11 show the six GWL-based RSLC median projections available from the two alternative methods, plus the two projections that include ice-sheet contributions based on SEJ available for one of the methods. In Extended Data Fig. 1, we also show the mean difference across the three ESL datasets between the present-day 100-yr and 1-yr ESL events, together with the standard deviation around it. The latter provides important context against which to evaluate the salience of the results we present below, since at some locations the difference is much smaller than at others. By design, our analysis does not extend to the evaluation of actual, location-specific impacts. Therefore, in the following, we do not highlight how large a change in the magnitude of the annual event at 2100 the enhanced frequency implies.
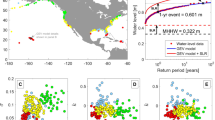
The central estimate of the GWL triggering the change in ESL frequency obtained by the voting system (akin to a majority vote, as described in the Methods) is shown in Fig. 1a. Already at 1.5 °C of warming by 2100 a large number of locations (54%; also Table 1, first row) will experience their present-day 100-yr ESL events annually (or more often). This is overwhelmingly true for locations in the southern hemisphere and the subtropics (Hawaii, the Maritime continent and the Caribbean) and the southern half of North America’s Pacific coast. However, a consideration of the uncertainties (Methods) shows that this frequency change would occur at up to 99% of locations in the most pessimistic lower bound produced by the voting system (Fig. 1c and Table 1, second row), while occurring at only 2% of locations for the optimistic upper bound (Fig. 1e and Table 1, third row). These bounding outcomes, akin to only asking for the vote of the single lowest GWL estimate, in the case of the pessimistic bound, or to requiring a unanimous vote in the case of the optimistic bound (as explained in the Methods) highlight the substantial level of disagreement among the six estimates, stemming from the wide ranges of the estimated present-day ESLs and the RSLC projections. Further considering the central estimate (Fig. 1a and Table 1, first row), an additional 11% of locations undergoes the change in frequency if global warming reaches 2 °C by 2100. But up to 7% of locations do not reach that annual frequency even for a warming of 5 °C and even if the SEJ-derived effects of ice-sheet dynamics are included (as all purple dots signify). Most of this last type of location are along the coastlines of Alaska and Northern Europe but are also found in regions exposed to tropical cyclone activity. Exposure to tropical cyclone activity makes the present-day ESL distributions wider (Extended Data Fig. 1) and therefore less sensitive to uniform shifts from RSLC. Further consideration of the upper bound shows that up to 70% of locations do not see the 100-fold increase in frequency for any of the considered GWLs, suggesting that at least one of the six estimates produces a more moderate frequency change even at the highest GWL considered.
a–f, GWLs reached by 2100 (distinguished by colour) causing the present-day 100-yr ESL event to become at least an annual event for 179 tide-gauge locations at which estimates are available from all three studies (a, c and e) and for 7,283 locations at which ESL estimates are available from the two model-based studies (b, d and f)). a, Central estimates for 179 tide-gauge locations for which all six alternative projections are available. b, Central estimate for 7,283 locations for which four alternative projections are available. c, Upper bound for the 179 locations. d, Upper bound for the 7,283 locations. e, Lower bound for the 179 locations. f, Lower bound for the 7,283 locations. Central estimates, lower and upper bound, as defined in the Methods, are shown from top to bottom respectively. The + sign associated with 2 and 5 °C indicates projections that include SEJ-derived estimates of ice-sheet contribution to RSLC.
Results for a much larger number of locations (7,283) at which four alternative projections are available and are combined through our voting system are presented in Fig. 1b,d,f and Table 1 (fourth to sixth rows). These have almost uniform global coverage, with an along-coast spacing of ~1° (~100 km at the equator; Methods). The differences between 100-yr and 1-yr events at this larger set of locations are shown in Extended Data Fig. 2.
The spatial dynamics shown by the analysis at the sparse subset of the tide-gauge locations (Fig. 1a,c,e and Table 1, first through third rows) appears to be representative of that along the global coastline (Fig. 1b,d,f and Table 1, fourth through sixth rows). Most of the tropics see the change in frequency from 100-yr to 1-yr (or more frequent) ESL event already at 1.5 °C of warming also for the larger set of locations, while the Northern Hemisphere high latitudes are again projected not to experience such a dramatic ESL frequency change, many even for the highest level of warming, and even with SEJ-derived ice-sheet contributions (as all purple dots signify). The greater coverage indicates that parts of the Mediterranean coasts and the Arabian Peninsula may also become ESL hotspots. A more complex picture emerges for some of the coastal areas, with a high level of along-coast variability; for example, along the Atlantic coast of North America, where the whole range of GWLs can result in the 100-fold change in frequency at nearby locations. The West coast of North America appears less sensitive to GWLs up to 5 °C and so does the Pacific coast of the Asian continent. Japan appears to experience a dichotomy between a sensitive West coast and its East coast, showing to endure the whole range of GWLs. Most of these features are reflected in the mean and standard deviation of the differences between 100-yr and 1-yr events shown in Supplementary Fig. 13. All this detail, however, does not translate in radically different distributions of the proportion of sites under the triggering GWLs, as a comparison of the corresponding rows in Table 1 shows. For the larger set of locations, the central estimate projects that 43% of locations will experience the present-day 100-yr ESL event at an annual or higher frequency even at 1.5 °C and that such a large frequency change will not occur at about 12% of the locations, even at the highest warming level (and even when including the effects of ice-sheet melt). The pessimistic lower bound estimate shows 99% of the locations experiencing the frequency change at 1.5 °C. The optimistic upper bound has only 7% experiencing this change at 1.5 °C and 60% avoiding the change altogether.
We test the robustness of this result by considering the outcomes of an alternative synthesis method, a full convolution that constructs a unique distribution of future ESLs from the six (or four) distributions that we have treated as individual expert voters in our approach so far. The full convolution could be seen as a more traditional approach at merging different probabilistic estimates but given the substantial differences in the individual estimates we propose our voting system as better suited at respecting such disagreements. Focusing on central estimates and lower and upper bounds available from both methods, a comparison of the histograms in Extended Data Fig. 3, left versus right column, indicates that the choice of synthesis method does not impact the lower bound (pessimistic) estimates (histograms in the third and fourth row) and only slightly changes the central estimate (top two rows) and the upper bound (bottom two rows). (The tractability of a single probability distribution rather than the need of reconciling four or six of them through our voting system, allows us to gain additional insights, by filling in intermediate quantiles to better represent the range of probabilistic outcomes. The distribution of GWLs including two intermediate quantiles, bounding 66% of probability, is shown in Supplementary Tables 4 and 5. As expected, the outcomes across GWLs are in these intermediate cases more evenly spread.)
Spatially, the differences emerging between the two approaches do not change the large-scale geographical patterns. Both methods confirm that the Atlantic coast of North America and the coasts of Northeast Asia are affected by a high degree of along-coast variability. These results are mapped in Extended Data Fig. 4.
Timing of the ESL frequency changes
Last, even if our analyses focussed on what happens at the time when the discrete set of warming levels are reached (2100), the availability of the corresponding RSLC timeseries over the twenty-first century (2020–2100) allows us to answer a further question, about when 100-yr to 1-yr ESL frequency changes are first observed. We stress, however, that the answer needs to be always conditional on the trajectories identified as being consistent with the individual GWLs. Supplementary Figs. 12 (for 1.5 °C) through 19 (for 5.0 °C) and Table 2 show the decade when the 100-fold frequency change is first observed, for the larger set of locations, and using the full-convolution approach. For the locations that are sensitive to even the lowest warming level of 1.5 °C—identified in our previous analysis mostly with the tropics and subtropics, that is, all locations not coloured in purple in Supplementary Fig. 12—most are projected by the central estimate to experience the shift between 2070 and 2080; for warmer GWLs up to 3.0 °C the 100-fold increase in frequency affects most sites one decade earlier, between 2060 and 2070. The highest GWLs (4.0 and 5.0 °C) cause most sites to experience the change between 2050 and 2060.
Discussion
We use a voting system, which we also compare to a more traditional full-convolution approach to synthesize alternative projections of ESL frequency changes (from 100-yr event at present to annual or more frequent by 2100) at a range of GWLs, for a large number of locations all along the world’s coastlines.
According to our central estimate, by the end of the century close to half of the locations considered will experience the present-day 100-yr ESL event at least once a year, even for a trajectory of global temperature that limits warming to 1.5 °C or at most 2 °C. The lower bound estimate sees practically all sites (98 or 99%) experiencing that dramatic change already for 1.5 °C. On the opposite end of the spectrum, an optimistic estimate sees about 60–70% of the locations avoiding such an increase in frequency altogether. Locations around the world can show very different behavior with respect to this change in frequency, either showing large sensitivities already at the lowest warming levels of 1.5 or 2 °C or being insensitive even up to the highest warming considered (5 °C), as about 7% of locations do not experience the frequency change, even when the possibility of rapid ice-sheet loss is included in the estimates of RSLC. We tested the sensitivity of this result to the approach taken to determine our ‘consensus’ by applying a more traditional convolution of the alternative probability distributions. The overall message does not change substantially. According to this last approach, we were also able to estimate the time at which the 100-fold increase in ESL frequency happens and we find that most of these locations will experience such change earlier than the end of the century, that is, in the decade between 2070 and 2080 according to our central estimate under the lowest GWL of 1.5 °C, one decade earlier for the intermediate GWLs and as early as 2060 for the highest GWLs of 4.0 and 5.0 °C. These last results are found to be very consistent with the analogous results shown in Fig. SPM4 of ref. 35, if one considers RCP 2.6 as a 2.0 °C end-of-century scenario and RCP 8.5 as a 4.0–5.0 °C end-of-century scenario36.
Coastlines in the tropics and parts of the Mediterranean and the Arabian Peninsula appear to be the places where these 100-fold changes in frequency of the 100-yr ESL events will take place even if 2100 warming is limited to 1.5 or 2 °C, consistent with previous studies that focused specifically on these lower levels of warming37. Parts of the coastal regions of the highest latitudes of both hemispheres are those where even higher levels of warming will not produce such frequency increases. While there may be localized exceptions, this means that, in terms of a 100-fold increase in the 100-yr ESL frequency, microtidal areas are highly sensitive to even the smaller GWLs considered here, while meso- and macro-tidal areas are not. The same applies for coastal areas that are either protected or exposed to meteorological extremes, with the former being more vulnerable to changing mean sea levels that expose them to unprecedented ESLs. The RSLC maps in the Supplementary Information also show that sea level is projected to increase above-average in many of these regions.
The coasts of North America and the coast of Northeast Asia appear to host a high degree of spatial variability in the results, with locations adjacent to one another either experiencing a large change in frequency at very low warming levels, or not experiencing it even for the highest warming levels considered here, calling for more indepth analysis and detailed modelling of the local dynamics. These geographically differentiated results are consistent with the analyses of refs. 11,16, which also highlighted similar differential sensitivities for return period changes due to RSLC. Topography and the history of extreme events experienced in the record at these locations are probably the source of such variations.
Our findings have important policy and practical implications as they highlight that even if the Paris Agreement goals will be achieved, extreme events potentially conducive to coastal flooding will be experienced at unprecedented frequencies in many parts of the world’s coasts. Only a very strict unanimity rule required of the alternative estimates produces substantially more optimistic projections. Our analysis was cast in terms of return period changes as return periods are typically the basis for coastal protection infrastructure design and hazard communication and therefore underline the potential need for global-scale adaptation efforts, even if our global assessment cannot match the detail and accuracy of local/regional studies. However, apart from allowing an indepth analysis of the spatial dynamics of sea-level rise using a globally homogeneous framework, our results allow the identification of ESL change ‘hotspots’ for which detailed dynamical modelling and a more indepth interpretation of the impact of changes in ESL hazard on human and natural systems38,39,40,41 are needed to serve local decisions.
Methods
Our analysis focuses on frequency changes of present-day 100-yr ESL events (events having 0.01 probability in any given year) at locations along the world’s ice-free coastline (Greenland, the Russian Arctic coast and Antarctica excluded).
At each location, future probabilistic estimates of RSLC are added to present-day probability distribution of ESLs. The addition has the first-order effect of shifting the distribution of ESLs uniformly and therefore changing the height of the 100-year event (and any other) by an offset equal to the amount of RSLC. The addition of an offset also changes the return period (the expected frequency) of the present-day 100-yr event, by making it more frequent if RSLC is positive or less frequent in the few locations and time periods where RSLC projections are negative. While the change in height of the future 100-yr event is by construction in our analysis the magnitude of RSLC, the change in frequency will depend on the interplay between the RSLC magnitude and the shape of the present-day ESL distribution. Importantly, all uncertainties in the parameters of the ESL distribution and the RSLC projections are taken into account.
All three studies used here for the ESL component fit peak-over-threshold Poisson-Generalized Pareto Distribution (GPD) models42 to present-day ESLs at each location. One of the original studies looked at alternative functional forms for the fit and concluded that the GPD had optimal properties17. Depending on the study, these ESLs are either observed from tide gauges or generated by hydrodynamic models that are validated with observations. Each Poisson-GPD model is characterized by four parameters: a threshold, determining the location of the distribution; a scale parameter, determining its width; a shape parameter, determining how fast the tail declines; and a rate parameter, determining the expected frequency of threshold exceedances. The addition of a positive amount of RSLC can be equivalently characterized as a decrease in the threshold by the same amount and therefore an increase in the likelihood of exceedances of a given height. The magnitude of the increase in the likelihood of occurrence of a given ESL caused by a given shift is determined by the scale and shape parameters.
If a quantity—in our case the extreme total water level1, which we here call ESL—follows the GPD, its probability distribution can be expressed as a function of three parameters: a threshold μ, a scale parameter σ and a shape parameter ξ. Consider \(z=\frac{x-\mu }{\sigma }\). Then, when z > 0
is the GPD density function. The additional parameter of interest that needs to be estimated to compute return periods is λ the Poisson rate of exceedance, indicating the expected annual number of events exceeding the threshold μ. According to the GPD definition, the expected number of events exceeding the threshold in a year is then
In our study, when we consider RSLC corresponding to year 2100 GWLs of 1.5, 2, 2.5, 3, 4 or 5°C above pre-industrial levels, we assume that those levels are reached by a gradual, non-decreasing trajectory of temperature change over the course of the twenty-first century.
Present-day ESL estimates from three previous studies
The three previously published studies that we use provide GPD parameters at locations around the world using the following approaches.
Vousdoukas et al. (2018)
This study16 uses the baseline period of 1980–2014 to generate realizations of the additive components of the total water levels (tidal elevation, wave setup and storm surges) by forcing a storm surge model and a wave model (Delft3D-FM (refs. 43,44) and WW3 (refs. 45,46) respectively) with ERA-INTERIM wind and pressure fields. Tropical cyclones effects are included in this baseline estimates by using satellite data (for wave heights) and simulating all historical tropical cyclones recorded during the 1980–2014 period (for storm surge) on the basis of the datasets available through the Hurricane Research Division of the National Oceanic and Atmospheric Administration (United States), the Joint Typhoon Warning Center and the UNISYS database (Data availability). These weather-driven components are added to the high-tide level at each location. A GPD is then fitted to these data. While here we use only the baseline period GPD parameters at each location, ref. 16 also estimate future changes in all the ESL components, by using CMIP5 model output and two emission scenarios to force the hydrodynamic models, but find that at most locations the main driver of change remains RSLC. The study relies on the preceding validation of the individual models used.
Kirezci et al. (2020)
This study17 combines global models of tide (FES2014, ref. 47), storm surge (GTSR, ref. 43) and waves (GOW2, ref. 48) to reconstruct the historical total water level at the DIVA coastal locations49,50 for the baseline period 1979–2014. Total water levels are defined as above, as the linear summation of tide, surge and wave setup. ESLs are determined by fitting ten different extreme value analysis methods and the global best fit is determined to be a GPD using the 98th-percentile threshold. Both the historical total water levels and the ESLs are rigorously validated against the quasi-global GESLA-2 tide-gauge observations51. The study does not consider possible future changes in storm surge heights and wave heights. Tropical cyclones effects are not included in these ESL estimates.
Rasmussen et al. (2018)
This study19, in contrast to the two previously described, relies only on observed hourly records of still water height to fit GPDs at a global network of about 200 tide gauges (University of Hawaii Sea Level Center (Data availability)). Only tide-gauge records of length >30 consecutive years and for which each year has >80% of observations available are considered. Unlike the above model-based approaches, this would neglect wave setup and swash contributions, both of which can be important contributors to ESLs52,53, unless the gauges are located nearshore. For each day in a given tide-gauge record with >12 h of data, the daily maximum sea level is estimated. Following ref. 32, the variation in ESLs is isolated by subtracting the annual mean sea level change from each daily maximum value (that is, values are detrended). The detrended daily maximum tide values are then referenced to local mean sea level. Daily maximum sea levels that are (1) above the 99th percentile and (2) within 3 d of each other are declustered to meet the statistical independence assumption of the GPD. The GPD is fitted to these daily maxima. Here, as in the previous two studies, future changes in storm frequency54, intensity55 or track56, which could all modify the GPD parameters, are not considered. Also not considered are changes in the tide-surge interaction53,57,58 or future changes in geomorphology, which can both impact the return periods of ESLs59,60.
Future RSLC estimates based on two previous studies
Our projections of future RSLC, geographically detailed, are obtained according to two methods developed in previously published studies but here applied to a wider range of GWLs.
Rasmussen et al. (2018)
This approach19 uses a set of local, probabilistic, RSLC projections conditional on each temperature target. Projections are made at a global tide-gauge network (Permanent Service for Mean Sea Level (Data availability)) as well as at the centre points of a 1° × 1° grid covering the coastlines of nearly all global landmasses, including several islands. The methodology of the projections follows the ‘bottom-up’, component-based framework of ref. 61, with modifications to accommodate temperature targets19,62 and estimates of dynamic ice-sheet melt from an SEJ exercise30.
Following ref. 19, temperature targets are accommodated by constructing alternative ensembles for each temperature scenario using Atmosphere-Ocean Global Climate Model (AOGCM) output filtered according to each AOGCM’s 2100 global mean surface air temperature. Specifically, AOGCM outputs from the CMIP5 archive63 are used for global mean thermal expansion, local ocean dynamics and as a driver of a surface mass balance model of glaciers and ice caps64. We detail the GCMs/RCPs used in Supplementary Tables 1–3. We create ensembles for 1.5, 2, 2.5, 3, 4 and 5 °C with AOGCMs that have a twenty-first-century global mean surface air temperature increase (19-yr running average) of 1.5 ± 0.25 °C, 2 ± 0.25 °C, 2.5 ± 0.25 °C, 3 ± 0.5 °C, 4 ± 0.5 °C and 5 ± 0.5 °C. For consistency with the ref. 61 framework, which models 19-yr running averages of SLC relative to 2000, anomalies of global mean surface air temperature from 1991 to 2009 are computed and then shifted upward by 0.72 °C to account for warming since 1875–190065. The global mean surface air temperature trajectories and global mean sea-level contributions from thermal expansion and glacial ice from selected CMIP5 models that are binned into each temperature target category are shown in Supplementary Figs. 20 and 21 respectively. Supplementary Tables 1–3 list the AOGCMs used in each temperature target ensemble, the RCP and the sea-level components derived.
Two different approaches are used for modelling contributions from ice-sheet melt. In the first approach, Antarctic Ice Sheet (AIS) and Greenland Ice Sheet (GIS) contributions are estimated by combining IPCC’s Fifth Assessment Report (AR5) ‘likely range’ projections of ice-sheet dynamics and surface mass balance (Table 13.5 in ref. 66) with information about distribution tail shape from an SEJ study of ice-sheet mass loss from ref. 67. Total ice-sheet contributions are computed by this approach for each temperature target considered in this study, by randomly sampling the AIS and GIS ice-sheet distribution for each RCP (Table 13.5 in ref. 66) in proportion to the representation of each RCP in the groups of CMIP5 models selected for each temperature target. For example, the 1.5 °C target uses 12 CMIP5 models from RCP 2.6 and two from RCP 4.5, so 86% of the samples are drawn from the RCP 2.6 distribution and 14% are drawn from the RCP 4.5 distribution (Supplementary Table 1).
In the second approach, which we apply only to projections for the 2 and 5 °C temperature targets, contributions from ice-sheet melt are obtained from the SEJ study of ref. 30. Projections of RSLC after mid-twenty-first century are highly dependent on ice-sheet melt because of its potential for substantial contributions to global mean sea-level rise5,68. However, incomplete understanding of the physical processes that govern ice-sheet melt inhibits realistic representations in process-based models. In such cases of incomplete scientific understanding, SEJ using calibrated expert responses is one approach for estimating such uncertain quantities (as used here). Note that we treat these two as additional levels of the GWL range and pair them with the same 2 and 5 °C estimates from the alternative method (not specifically containing SEJ ice-sheet melt estimates) when synthesizing through the voting or the convolution methods.
Vega-Westhoff et al. (2019)
RSLC projections from this approach27 are from a recent perturbed physics ensemble using the reduced complexity climate model Hector-BRICK26,27,69. The model includes a one-dimensional diffusive heat and energy balance model, combined with a sea-level change module that represents contributions from thermal expansion, glaciers and small ice caps and polar ice sheets. The model also includes a simple parameterization of fast ice-sheet dynamic disintegration in the Antarctic ice-sheet component26. We estimate 39 uncertain parameters using a Bayesian calibration method (adaptive Markov Chain Monte Carlo), with observational constraints from global surface temperature, global ocean thermal expansion and polar land ice. The ensemble and applications are discussed in more detail in refs. 27,28.
Here we sample 10,000 parameter combinations from the joint posterior distribution. For each parameter combination, we force the model with RCP 2.6, RCP 4.5, RCP 6 and RCP 8.5 radiative forcings. We create ensembles by sorting these simulations into bins of twenty-first-century global mean temperature increase (19-yr running average) of 1.5 ± 0.25 °C, 2 ± 0.25 °C, 2.5 ± 0.25 °C, 3 ± 0.5 °C, 4 ± 0.5 °C and 5 ± 0.5 °C.
Hector-BRICK simulates global sea-level rise, so gridded and local tide-gauge estimates (Permanent Service for Mean Sea Level (Data availability)) are constructed from Hector-BRICK results using a fingerprinting technique that accounts for regional variability due to mass redistribution from melting land ice28,70. For this fingerprinting, we assume land water storage and ocean thermal expansion are globally uniform and we neglect changes in local ocean dynamics. We also assume that contributions from Antarctica and Greenland are uniform over their respective ice-sheet surfaces. We also neglect the possibility of different paces of mass change for different glacier regions over the twenty-first century.
Both of the methods produce RSLC projections at the same set of tide gauges used in ref. 19 and in addition cover a regular 1° × 1° grid over the world’s coastlines. Both methods produce projections in the form of an empirical distribution of values generated through Monte Carlo sampling.
The methods can produce substantially different projections, especially in the high latitudes (Supplementary Figs. 4–10). We attribute these large differences to two reasons. First, the methods use two different approaches for accounting for non-climatic vertical land motion. Following ref. 61, ref. 19 uses a spatiotemporal Gaussian process model to account for background rates of vertical land motion. This includes deltaic processes, tectonic uplift, anthropogenic subsidence processes (for example, ground water and fossil fuel withdrawal) and glacial isostatic adjustment. On the other hand, ref. 27 only considers glacial isostatic adjustment estimates from ref. 70. Second, the two methods consider different estimates of GIS melt and AIS melt. For example, ref. 27 considers a median estimate for AIS melt that is nearly 0.5 m larger than for ref. 19. Greater ice-sheet melt can amplify differences in RSLC due to gravitational-rotational and deformational effects1.
Matching the two components and computing future frequencies
The GPDs estimated by each of the three studies include measures of standard errors for the parameters and the 100-yr event. To sample from the distributions fully accounting for the uncertainty in the parameters, we use an asymptotic approximation to their covariance matrix based on the Fisher information matrix, as presented in refs. 71. The Fisher information matrix, when calculated at the maximum likelihood estimates of the parameters, can be interpreted as the inverse of the covariance matrix estimate and in our notation takes the simple form
where N is the expected total number of exceedances, estimated by λ multiplied by the number of years used in the estimation.
The approximation is valid as long as ξ > −0.5 which is true for all but a handful of locations, which we discard.
We therefore resample at each location pairs of the shape and scale parameters according to a normal distribution with mean their maximum likelihood estimates and covariance matrix (equation (3)), and for each pair we derive the corresponding value of the 100-yr event. We then match them with as many random samples from the RSLC distributions.
For each location and each sample i, given the magnitude of the present-day 100-year event, xi, the four parameters of the GPD, μ, σi, ξi and λ and the magnitude of RSLC by 2100 for a given warming target, si, the new frequency RP(xi) (RP, return period) can be computed as
where \(\mu ^{\prime} =\mu +{s}_{i}.\)
A population of samples large enough to characterize future statistics robustly (we use 1,000 after verifying that larger samples would not change substantially our results) is computed separately for each of the six combinations of the three sets of ESL estimates and the two sets of RSLC estimates.
Note that the use of this formula caps the highest obtainable frequency to the 1-year return period. Therefore, by construction that is going to be the highest future frequency projected by our approach, even if some locations could experience present-day 100-year ESL events more often than once a year under different GWLs19. Consequently, when throughout the paper we use the expressions 1-yr, or annual, ESL event, we have added wording to the effect that this is a lower estimate of the possible change in frequency.
Synthesizing
For a subset of 179 locations, and for a given warming level, we have six full probability distributions of future (2100) return periods of the current 100-yr ESL event, one for each combination of the three ESL estimates with the two RSLC estimates. For a much larger set of 7,283 locations we have four, as the observation-based ESL estimates from ref. 19 are only available for the subset of 179 common locations.
By considering the evolution of these distributions across the discrete set of GWLs at 2100, it is possible to pinpoint the warming level, if any, at which the current 100-yr event becomes an annual (or more frequent) event. Estimates derived are by construction not deterministic but hinge on choosing a level of confidence, for example, a quantile of the six distributions and some form of ‘voting’ among them.
We use the following three ways to synthesize this complex set of projections at each location where all six probabilistic estimates are available.
-
1.
For each 2100 warming level, we consider the median value (50th quantile) of each of the six distributions of future return periods and we will take the lowest warming level for which most of the six medians predict a change from 100-yr to 1-yr (that is, at least four of the medians are equal to 1-yr RP). This will be our ‘central estimate’ of the warming level at which the frequency of the current 100-yr event becomes annual (or higher). This estimate could be characterized as a majority vote (using the medians of the distributions as the individual votes).
-
2.
For each 2100 warming level, we will consider the 5th quantile of each of the the six distributions. This choice represents a ‘worst case’ because it favours low values in the distribution, translating to a short return period, and therefore a high frequency. Our voting system in this case will pick the most pessimistic of the six estimates; that is, we will choose the lowest warming level at which the minimum of the six 5th quantiles is equal to 1-yr RP. This will be the pessimistic (lower) bound of our estimates. This estimate can be characterized as taking the most extreme (in a negative sense) of the alternative estimates; that is, using a low value of the most sensitive distribution.
-
3.
For each 2100 warming level, we will consider the 95th quantile of each of the six distributions. Mirroring the pessimistic case above, this choice represents a ‘best case’ because it favours large values in the distribution, translating to a long return period and therefore a lower frequency. Our voting system in this case will pick the lowest warming level at which the maximum of the six 95th quantiles is 1-yr RP. This will constitute our optimistic upper bound estimate. Note that by definition requiring the maximum to be 1 is equal to requiring that all six 95th quantiles are equal to 1; that is, we require unanimity among the individual votes.
We apply this synthesis to the 179 locations at which all three ESL estimates are available (we define one available if it produces an estimate at a location within a distance less than a (spatial) degree, which is also the criterion for matching RSLC and ESLs estimates). We then show the same synthesis (with the required modification in defining the majority vote out of four) applied to the 7,283 locations at which both ESL estimates based on hydrodynamic modelling are available but not the observation-based one.
An alternative, more conventional, approach to synthesizing these multiple distributions is to consider them equally likely and combine them by Monte Carlo sampling into a single full-convolution distribution, for which median and quantiles of interest can be extracted. We perform this alternative approach as well, by sampling 1,000 values from the individual distribution with equal weights and discuss differences in the outcomes of the two synthesis approaches.
Data availability
Datasets containing ESLs and SLRC matched for this study are available from https://github.com/DOE-ICoM/tebaldi-etal_2021_natclimchange. Data from the Hurricane Research Division of the National Oceanic and Atmospheric Administration are available at http://www.aoml.noaa.gov/hrd/hurdat/Data_Storm.html; data from the Joint Typhoon Warning Center are available at https://www.metoc.navy.mil/jtwc/jtwc.html?best-tracks/ and the UNISYS database is available at https://cmr.earthdata.nasa.gov/search/concepts/C1214612507-SCIOPS. The University of Hawaii Sea Level Center data are available at https://doi.org/10.7289/V5V40S7W. The Permanent Service for Mean Sea Level data are available at https://www.psmsl.org.
Code availability
The R code72 used for the analysis and graphics of this paper is available from https://github.com/DOE-ICoM/tebaldi-etal_2021_natclimchange.
Change history
12 April 2023
A Correction to this paper has been published: https://doi.org/10.1038/s41558-023-01665-w
References
Gregory, J. M. et al. Concepts and terminology for sea level: mean, variability and change, both local and global. Surv. Geophys. 40, 1251–1289 (2019).
Hallegatte, S., Green, C., Nicholls, R. J. & Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Change 3, 802–806 (2013).
Hinkel, J. et al. Coastal flood damage and adaptation costs under 21st century sea-level rise. Proc. Natl Acad. Sci. USA 111, 3292–3297 (2014).
Ranasinghe, R. Assessing climate change impacts on open sandy coasts: a review. Earth Sci. Rev. 160, 320–332 (2016).
Oppenheimer, M. et al. in IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (eds Portner, H.-O. et al.) Ch. 4 (Cambridge Univ. Press, in the press).
Vousdoukas, M. I. et al. Economic motivation for raising coastal flood defenses in Europe. Nat. Commun. 11, 2119 (2020).
Jevrejeva, S., Jackson, L. P., Riva, R. E. M., Grinsted, A. & Moore, J. C. Coastal sea level rise with warming above 2 °C. Proc. Natl Acad. Sci. USA 113, 342–347 (2016).
Vousdoukas, M. I. et al. Climatic and socioeconomic controls of future coastal flood risk in Europe. Nat. Clim. Change 8, 776–780 (2018).
Vousdoukas, M. I. et al. Sandy coastlines under threat of erosion. Nat. Clim. Change 10, 260–263 (2020).
Wahl, T. et al. Understanding extreme sea levels for broad-scale coastal impact and adaptation analysis. Nat. Commun. 8, 16075 (2017).
Vitousek, S. et al. Doubling of coastal flooding frequency within decades due to sea-level rise. Sci. Rep. 7, 1399–1399 (2017).
Muis, S. et al. A high-resolution global dataset of extreme sea levels, tides, and storm surges, including future projections. Front. Mar. Sci. 7, 263 (2020).
Brown, S., Nicholls, R. J., Lowe, J. A. & Hinkel, J. Spatial variations of sea-level rise and impacts: an application of DIVA. Climatic Change 134, 403–416 (2016).
Buchanan, M. K., Oppenheimer, M. & Kopp, R. E. Amplification of flood frequencies with local sea level rise and emerging flood regimes. Environ. Res. Lett. 12, 064009 (2017).
Lincke, D. & Hinkel, J. Economically robust protection against 21st century sea-level rise. Glob. Environ. Change 51, 67–73 (2018).
Vousdoukas, M. I. et al. Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat. Commun. 9, 2360 (2018).
Kirezci, E. et al. Projections of global-scale extreme sea levels and resulting episodic coastal flooding over the 21st century. Sci. Rep. 10, 11629 (2020).
Tiggeloven, T. et al. Global-scale benefit–cost analysis of coastal flood adaptation to different flood risk drivers using structural measures. Nat. Hazards Earth Syst. Sci. 20, 1025–1044 (2020).
Rasmussen, D. J. et al. Extreme sea level implications of 1.5 °C, 2 °C, and 2.5 °C temperature stabilization targets in the 21st and 22nd centuries. Environ. Res. Lett. 13, 034040 (2018).
Jackson, L. P., Grinsted, A. & Jevrejeva, S. 21st century sea-level rise in line with the Paris accord. Earth’s Future 6, 213–229 (2018).
Nicholls, R. J. et al. Stabilization of global temperature at 1.5 °C and 2 °C: implications for coastal areas. Phil. Trans. R. Soc. A 376, 20160448 (2018).
Feng, J. et al. Changes of extreme sea level in 1.5 and 2.0 °C warmer climate along the coast of china. Front. Earth Sci. 6, 216 (2018).
Report of the Conference of the Parties on its Twenty-first Session (United Nations, 2015); https://unfccc.int/resource/docs/2015/cop21/eng/10.pdf
Report on the Structured Expert Dialogue on the 2013–2015 Review (United Nations, 2015); https://unfccc.int/resource/docs/2015/sb/eng/inf01.pdf
Hermans, T. H. J. et al. Projecting global mean sea-level change using CMIP6 models. Geophys. Res. Lett. 48, e2020GL092064 (2021).
Wong, T. E. et al. BRICK v0.2, a simple, accessible, and transparent model framework for climate and regional sea-level projections. Geosci. Model Dev. 10, 2741–2760 (2017).
Vega-Westhoff, B., Sriver, R. L., Hartin, C. A., Wong, T. E. & Keller, K. Impacts of observational constraints related to sea level on estimates of climate sensitivity. Earth’s Future 7, 677–690 (2019).
Vega-Westhoff, B., Sriver, R. L., Hartin, C., Wong, T. E. & Keller, K. The role of climate sensitivity in upper-tail sea level rise projections. Geophys. Res. Lett. 47, e2019GL085792 (2020).
DeConto, R. M. & Pollard, D. Contribution of Antarctica to past and future sea-level rise. Nature 531, 591–597 (2016).
Bamber, J. L., Oppenheimer, M., Kopp, R. E., Aspinall, W. P. & Cooke, R. M. Ice sheet contributions to future sea-level rise from structured expert judgment. Proc. Natl Acad. Sci. USA 116, 195–200 (2019).
Le-Cozannet, G., Manceau, J.-C. & Rohmer, J. Bounding probabilistic sea-level projections within the framework of the possibility theory. Environ. Res. Lett. 12, 014012 (2017).
Tebaldi, C., Strauss, B. H. & Zervas, C. E. Modelling sea level rise impacts on storm surges along US coasts. Environ. Res. Lett. 7, 014032 (2012).
Buchanan, M. K., Kopp, R. E., Oppenheimer, M. & Tebaldi, C. Allowances for evolving coastal flood risk under uncertain local sea-level rise. Climatic Change 137, 347–362 (2016).
Lang, A. & Mikolajewicz, U. The long-term variability of extreme sea levels in the German Bight. Ocean Sci. 15, 651–668 (2019).
IPCC in IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (eds Portner, H.-O. et al.) (Cambridge Univ. Press, in the press); https://www.ipcc.ch/srocc/
Tebaldi, C. et al. Climate model projections from the Scenario Model Intercomparison Project (ScenarioMIP) of CMIP6. Earth Syst. Dynam. 12, 253–293 (2021).
Frederikse, T. et al. Antarctic ice sheet and emission scenario controls on 21st -century extreme sea-level changes. Nat. Commun. 11, 390 (2020).
Wong, T. E. & Keller, K. Deep uncertainty surrounding coastal flood risk projections: a case study for New Orleans. Earth’s Future 5, 1015–1026 (2017).
Ruckert, K. L., Srikrishnan, V. & Keller, K. Characterizing the deep uncertainties surrounding coastal flood hazard projections: a case study for Norfolk, VA. Sci. Rep. 9, 1 (2019).
Woodworth, P. L. et al. Forcing factors affecting sea level changes at the coast. Surv. Geophys. 40, 1351–1397 (2019).
Bevacqua, E. et al. More meteorological events that drive compound coastal flooding are projected under climate change. Commun. Earth Environ. 1, 47 (2020).
Coles, S. An Introduction to Statistical Modeling of Extreme Values (Springer-Verlag, 2001).
Muis, S. et al. A global reanalysis of storm surges and extreme sea levels. Nat. Commun. 7, 11969 (2016).
Lima Rego, J. et al. A Global Tide and Storm Surge Model with a Parallel Unstructured-Grid Shallow Water Solver in American Geophysical Union, Fall Meeting abstr. OS21E-05 (2014).
Mentaschi, L., Vousdoukas, M. I., Voukouvalas, E., Dosio, A. & Feyen, L. Global changes of extreme coastal wave energy fluxes triggered by intensified teleconnection patterns. Geophys. Res. Lett. 44, 2416–2426 (2017).
Vousdoukas, M. I., Mentaschi, L., Voukouvalas, E., Verlaan, M. & Feyen, L. Extreme sea levels on the rise along Europe’s coasts. Earth’s Future 5, 304–323 (2017).
Carrere, L., Lyard, F., Cancet, M., Guillot, A. & and Picot, N. FES2014, A New Tidal Model—Validation Results and Perspectives for Improvements Living Planet Symposium (ESA, 2016); http://lps16.esa.int/page_paper1956.php
Perez, J., Menendez, M. & Losada, I. J. GOW2: a global wave hindcast for coastal applications. Coast. Eng. 124, 1–11 (2017).
Vafeidis, A. T. et al. A new global coastal database for impact and vulnerability analysis to sea-level rise. J. Coast. Res. 24, 917–924 (2008).
Hinkel, J. & Klein, R. J. Integrating knowledge to assess coastal vulnerability to sea-level rise: the development of the DIVA tool. Glob. Environ. Change 19, 384–395 (2009).
Woodworth, P. L. et al. GESLA (Global Extreme Sea Level Analysis) high frequency sea level dataset—Version 2 (British Oceanographic Data Centre—Natural Environment Research Council, 2016); https://doi.org/10.5285/3b602f74-8374-1e90-e053-6c86abc08d39
Melet, A., Meyssignac, B., Almar, R. & Le Cozannet, G. Under-estimated wave contribution to coastal sea-level rise. Nat. Clim. Change 8, 234–239 (2018).
Arns, A. et al. Sea-level rise induced amplification of coastal protection design heights. Sci. Rep. 7, 40171 (2017).
Walsh, K. J. et al. Tropical cyclones and climate change. WIREs Clim. Change 7, 65–89 (2016).
Sobel, A. H. et al. Human influence on tropical cyclone intensity. Science 353, 242–246 (2016).
Garner, A. J. et al. Impact of climate change on New York City’s coastal flood hazard: increasing flood heights from the preindustrial to 2300 CE. Proc. Natl Acad. Sci. USA 114, 861–866 (2017).
Arns, A. et al. Non-linear interaction modulates global extreme sea levels, coastal flood exposure, and impacts. Nat. Commun. 11, 1918 (2020).
Schindelegger, M., Green, J. A. M., Wilmes, S.-B. & Haigh, I. D. Can we model the effect of observed sea level rise on tides? J. Geophys. Res. Oceans 123, 4593–4609 (2018).
Familkhalili, R. & Talke, S. A. The effect of channel deepening on tides and storm surge: a case study of Wilmington, NC. Geophys. Res. Lett. 43, 9138–9147 (2016).
Talke, S. A., Orton, P. & Jay, D. A. Increasing storm tides in New York harbor, 1844–2013. Geophys. Res. Lett. 41, 3149–3155 (2014).
Kopp, R. E. et al. Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earth’s Future 2, 383–406 (2014).
Bittermann, K., Rahmstorf, S., Kopp, R. E. & Kemp, A. C. Global mean sea-level rise in a world agreed upon in Paris. Environ. Res. Lett. 12, 124010 (2017).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498 (2012).
Marzeion, B., Jarosch, A. H. & Hofer, M. Past and future sea-level change from the surface mass balance of glaciers. Cryosphere 6, 1295–1322 (2012).
Hansen, J., Ruedy, R., Sato, M. & Lo, K. Global surface temperature change. Rev. Geophys. https://doi.org/10.1029/2010RG000345 (2010).
Church, J. et al. in Climate Change 2013: The Physical Science Basis (eds Stocker, T. F. et al.) 1137–1216 (Cambridge Univ. Press, 2013).
Bamber, J. L. & Aspinall, W. P. An expert judgement assessment of future sea level rise from the ice sheets. Nat. Clim. Change 3, 424–427 (2013).
Kopp, R. E. et al. Usable science for managing the risks of sea-level rise. Earth’s Future 7, 1235–1269 (2019).
Hartin, C. A., Patel, P., Schwarber, A., Link, R. P. & Bond-Lamberty, B. P. A simple object-oriented and open-source model for scientific and policy analyses of the global climate system—Hector v1.0. Geosci. Model Dev. 8, 939–955 (2015).
Slangen, A. B. A. et al. Projecting twenty-first century regional sea-level changes. Climatic Change 124, 317–332 (2014).
Davison, A. C. & Smith, R. Models for exceedances over high thresholds. J. R. Stat. Soc. B 52, 393–442 (1990).
R Core Team. R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, 2019); https://www.R-project.org/
Acknowledgements
C.T.’s work was supported by the Multisector Dynamics program area of the US Department of Energy, Office of Science, Office of Biological and Environmental Research as part of the multi-programme, collaborative Integrated Coastal Modeling (ICoM) and by US Environmental Protection Agency, under Interagency Agreement DW-089-92459801. R.R. is supported by the AXA Research fund and the Deltares Strategic Research Programme ‘Natural Hazards’. Data and code supporting this paper were archived with the support of the MultiSector Dynamics-Living, Intuitive, Value-adding Environment (MSD-LIVE) project.
Author information
Authors and Affiliations
Contributions
C.T. and R.R. planned the study. D.J.R. and B.V.W. produced new RSLC projections according to the range of GWLs. All authors M.V., D.J.R., E.K., B.V.W., B.K., R.S. and L.M., of the previous studies constituting the building blocks contributed their individual pieces. C.T. performed the synthesis and structured and wrote the manuscript. All authors contributed to the editing and refinement of the narrative and context of the study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Climate Change thanks Job Dullaart, Mamunur Rashid and Aimée Slangen for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Differences between 100-yr and 1-yr events.
For the subset of 179 locations at which all three ESL datasets are available, mean value (top panel) and standard deviation (bottom panel) of the difference between current 100-yr and 1-yr current events.
Extended Data Fig. 2 Differences between 100-yr and 1-yr events.
For the subset of 7,283 locations at which the two datasets based on modelling of current ESL are available, mean value (top panel) and standard deviation (bottom panel) of the difference between current 100-yr and the 1-yr events.
Extended Data Fig. 3 Histograms of the distribution of the number of sites at which a 100-fold increase in the frequency of the present-day 100-yr ESL event occurs for each warming level.
Results are shown for two alternative synthesis methods, the voting system (left column) and the full convolution (right column). The histograms along each column are organized in pairs, with the first pair showing the central estimate ((a)-(d)) the second pair showing the lower bound ((e)-(h)) and the third and last pair showing the upper bound ((i)-(l)). For each pair, the upper histogram shows the results for the smaller set of 179 sites, the lower histogram shows the results for the larger set of 7,283 sites.
Extended Data Fig. 4 As Fig. 1 but using a full convolution.
Combining all four distributions into an overall distribution by a full convolution, GWLs reached by 2100 (distinguished by colour) causing the present-day 100-yr ESL event to become at least annual, for 179 locations at which ESL estimates from all 3 studies are available (left column) and for the 7,283 locations for which the model-based ESL estimates are available (right column). Central estimate (median),lower and upper bounds (that is, 5th and 95th quantiles) are shown from top to bottom respectively. The + sign associated to 2°C and 5°C indicates projections that include SEJ-derived estimates of ice-sheet contribution to SLC.
Supplementary information
Supplementary Information
Supplementary Figs. 1–21 and Tables 1–5.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tebaldi, C., Ranasinghe, R., Vousdoukas, M. et al. Extreme sea levels at different global warming levels. Nat. Clim. Chang. 11, 746–751 (2021). https://doi.org/10.1038/s41558-021-01127-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41558-021-01127-1
This article is cited by
-
Stochastic simulation of storm surge extremes along the contiguous United States coastlines using the max-stable process
Communications Earth & Environment (2024)
-
Stochastic coastal flood risk modelling for the east coast of Africa
npj Natural Hazards (2024)
-
The carbon emission reduction effect of green fiscal policy: a quasi-natural experiment
Scientific Reports (2024)
-
The risk of concurrent heatwaves and extreme sea levels along the global coastline is increasing
Communications Earth & Environment (2024)
-
Causes and multiyear predictability of the rapid acceleration of U.S. Southeast Sea level rise after 2010
npj Climate and Atmospheric Science (2024)