Abstract
Amorphous calcium carbonate is an important precursor for biomineralization in marine organisms. Key outstanding problems include understanding the structure of amorphous calcium carbonate and rationalizing its metastability as an amorphous phase. Here we report high-quality atomistic models of amorphous calcium carbonate generated using state-of-the-art interatomic potentials to help guide fits to X-ray total scattering data. Exploiting a recently developed inversion approach, we extract from these models the effective Ca⋯Ca interaction potential governing the structure. This potential contains minima at two competing distances, corresponding to the two different ways that carbonate ions bridge Ca2+-ion pairs. We reveal an unexpected mapping to the Lennard-Jones–Gauss model normally studied in the context of computational soft matter. The empirical model parameters for amorphous calcium carbonate take values known to promote structural complexity. We thus show that both the complex structure and its resilience to crystallization are actually encoded in the geometrically frustrated effective interactions between Ca2+ ions.

Similar content being viewed by others
Main
Calcium carbonate is relatively unusual among simple inorganic salts in that it precipitates from aqueous solution in a metastable hydrated, amorphous form1. Amorphous calcium carbonate (ACC)—with a nominal composition of CaCO3⋅xH2O (x ≈ 1)—can be stabilized for weeks by incorporating dopants such as Mg2+ or PO43− (refs. 2,3), or alternatively directed to crystallize into a number of different polymorphs by varying the pH or temperature4. Nature exploits this complex phase behaviour in a variety of biomineralization processes to control the development of shells and other skeletal structures5,6. Not only does the amorphous nature of biogenic ACC allow transformation to different crystalline CaCO3 polymorphs, but it helps organisms fashion larger-scale hierarchical morphologies that are important in biomineral architectures7. In seeking to develop bio-inspired crystal-engineering approaches for synthetic control over phase and morphology selection, there is an obvious need to understand why such a chemically simple system can exhibit such complex phase behaviour.
One domain in which a similar kind of phase complexity has been studied deeply from a theoretical perspective is that of soft-matter systems governed by multi-well pair potentials. Whereas isotropic particles that interact via a simple single-well potential (for example, Lennard-Jones, LJ) self-assemble into structurally simple crystalline phases (for example, face-centred cubic), the inclusion of one or more additional energy minima to the interaction potential can drive remarkable complexity if the distances at which these minima occur lead to geometric frustration8,9,10,11. An elegant example in two dimensions is that of quasicrystal self-assembly for specific parameters of the double-well Lennard-Jones–Gauss (LJG) potential8,12. In three dimensions, the same interaction model can be tuned to stabilize complex crystals with enormous unit cells11, and some combinations of the LJ and Gauss well positions even appear to frustrate crystallization altogether9.
That competing length scales might be relevant to ACC is a point hinted at by the observation of two preferred Ca⋯Ca distances dominating medium-range order in synthetic ACC13,14. These two distances are directly evident in the experimental X-ray pair distribution function (PDF) of ACC and are attributed to different bridging modes of the carbonate ion, which can connect a pair of Ca2+ ions either directly through one of the oxygen atoms (Ca–O–Ca pathway) or by inserting the carbonate ion fully between the cations (Ca–O–C–O–Ca pathway).
In this Article we explore the possibility that the structure of ACC is governed by effective interactions between Ca2+ ions that also reflect these two length scales, and that its well-known complexity emerges because the distances involved are in competition with one another. Our approach begins by obtaining a high-quality measure of the Ca-pair correlation function in ACC. We do this by applying a hybrid reverse Monte Carlo (HRMC) approach15 to generate the first structural model of ACC that is simultaneously consistent with experiment and stable with respect to state-of-the-art potentials. The Ca-pair correlation function that emerges is then inverted using a recently developed algorithm16 to reveal the effective, carbonate/water-mediated Ca⋯Ca interaction potential. We find that this potential is closely related to the LJG formalism, with empirical parameters that are known to frustrate crystallization. Monte Carlo (MC) simulations driven by our LJG model yield coarse-grained representations of ACC that capture key aspects of our fully atomistic HRMC models. In this way, we explain the structural complexity of ACC in terms of geometric frustration of two competing energetically favoured Ca⋯Ca separations. Mapping the problem of ACC structure onto the phase behaviour of multi-well potentials is important not only because it establishes the first experimental system for which these potentials are relevant, but also because it suggests how structural complexity in inorganic phases might be controllably targeted through suitable tuning of effective interactions.
Results
Structure of ACC
Our HRMC refinements made use of atomistic configurations containing 12,960 atoms (1,620 CaCO3⋅H2O formula units), with simulation cell sizes of ~5 nm. During refinement, atomic moves were proposed and then rejected or accepted according to a Metropolis Monte Carlo criterion, with a cost function that measured the quality of fit to X-ray total scattering data17 and also the energetic stability evaluated using the state-of-the-art interatomic potential of ref. 18. We favoured an HRMC approach over empirical potential structure refinement (EPSR), because calcium carbonate potentials are notoriously delicately balanced18, such that EPSR-derived potentials are unlikely to be physically meaningful for this system. To allow for direct comparison with previous studies, we used a weighted variant of the experimental X-ray total scattering function (that is, QFX(Q)) of synthetic ACC reported in ref. 13, which has been shown to be indistinguishable from that obtained for biogenic ACC samples19. For consistency, our HRMC configuration size and refinement constraints were also identical to those used in the reverse Monte Carlo (RMC) investigation of synthetic ACC in ref. 14. The absence of key energetic considerations in that RMC study allowed the development of physically unreasonable charge separation to give a model of cationic Ca2+-rich domains separated by channels of carbonate anions and water molecules. Our expectation was that the explicit consideration of electrostatics in our HRMC implementation would guide refinement towards a solution that was equally consistent with experiments, but also energetically sensible.
HRMC does indeed find a suitable compromise between experiment and theory. We show in Fig. 1a the QFX(Q) function calculated from a representative configuration, and compare it to the equivalent functions predicted using pure RMC refinement, on the one hand, and unconstrained molecular dynamics (MD) simulations with the potentials of ref. 18, on the other hand. Both RMC and HRMC give very similar high-quality fits to experiment—unsurprising, of course, as they have been refined against these data. The MD simulation, however, misses some aspects of the QFX(Q) function. By contrast, the HRMC and MD models give similar cohesive energies, whereas the RMC model is less stable than both by more than 800 kJ mol−1 per formula unit. These results are summarized in Fig. 1b, which captures the motivation for our use of HRMC as a suitable balancing act: it has, for the first time, allowed access to an atomistic representation of ACC structure that is consistent with experiment and gives sensible energies using established hydrated calcium carbonate potentials. We also checked whether the HRMC model could reproduce the neutron total scattering data of refs. 20,21,22 (it can—see Supplementary Fig. 1 and Supplementary Discussion 1) and whether it is stable in MD simulations driven by the potentials of ref. 18 (it is—see Extended Data Fig. 1).
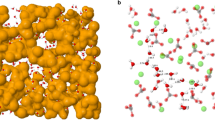
a, The experimental Q-weighted X-ray total scattering function QFX(Q) is well fitted by both RMC (top trace) and HRMC (middle) refinements, but is meaningfully different to that calculated using the interatomic potential of ref. 18 (bottom). Experimental data are shown as black lines, and fits or calculations as red lines. b, Quality criteria for the different structural models. HRMC simultaneously optimizes both goodness-of-fit to experimental data (χ2) and cohesive energy (Erel), and therefore finds a structure solution that is essentially as consistent with experiment as that obtained using RMC, while also as energetically sensible as that obtained using potentials alone (MD). c, Representation of a converged structure of ACC obtained using HRMC. Water molecules connect to form filamentary strands (aquamarine strings) that separate calcium carbonate-rich domains (Ca atoms are shown as large beige spheres, and carbonate ions as stick representation).
The HRMC model itself is illustrated in Fig. 1c. We observe that water is not homogeneously distributed throughout the configuration, but rather that the ACC structure consists of CaCO3-rich regions separated by a filamentary network of water: we term this a ‘blue cheese’ model. Qualitatively similar descriptions were obtained in MD simulations23, in EPSR refinements of combined neutron/X-ray total scattering data22, and also inferred from solid-state NMR measurements24. In all cases, the interpretation is that nearly all H2O molecules are bound to Ca2+ (as implied by 1H NMR; ref. 25), but neighbouring water molecules are sufficiently close to form a network that percolates the ACC structure. As anticipated, the charge separation that developed in the RMC model of ref. 14 has now vanished: the water-rich filaments we observe do not contain any free carbonate and are substantially narrower than the nanopore channels reported previously. The fact that RMC and HRMC models give similar QFX(Q) fits despite their very different descriptions of the structure reflects the difficulty of discriminating between C and O atoms using X-ray scattering methods alone26.
Locally, our HRMC model shows coordination environments that are consistent with the consensus of recent computational and experimental studies. For completeness, we show in Fig. 2a,b the distribution of calcium and carbonate coordination numbers. The average Ca2+ coordination number of 7.0—defined for a cutoff distance of 2.8 Å—is similar to that reported in refs. 22,27,28. Whereas most Ca2+ bind either five or six distinct carbonate anions, the carbonates tend to bind one fewer Ca2+ ion each, reflecting a binding-mode distribution of ~80:20 monodentate:bidentate. Representative modal coordination geometries for Ca2+ and CO32− are shown in Fig. 2c,d. As anticipated14, we find that carbonate anions bridge calcium-ion pairs in two ways: either a pair of Ca2+ ions share a common carbonate oxygen neighbour, or they bind distinct oxygens and so are connected formally by a Ca–O–C–O–Ca pathway. A full analysis of coordination environments, including bond-length and bond-angle distributions, is provided in Extended Data Figs. 1–4 and Supplementary Discussions 2 and 3.
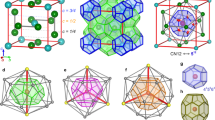
a, Histogram of Ca2+ coordination environments, decomposed into contributions from carbonate and water oxygen donors (Oc and Ow, respectively). b, Histogram of CO32− coordination environments, now decomposed into contributions from Ca2+ and water hydrogen donors (Hw). c, Representative Ca2+ coordination sphere for the modal coordination environment marked by a star in a. d, Representative CO32− coordination sphere for the modal coordination environment marked by a star in b. Note that pairs of Ca2+ ions within the same CO32− coordination sphere either share a common oxygen donor (for example, red arrow) or are connected by Ca–O–C–O–Ca pathways (for example, blue arrow). Ca, C, O and H atoms are shown in beige, grey, aquamarine and white, respectively. e, Ca-pair correlation functions gCa(r) extracted from HRMC, RMC and LJG configurations, compared against the normalized Fourier transform of the experimental X-ray total scattering function (which includes contributions from all atom pairs, for example, the Ca–O peak at 2.4 Å marked with an asterisk). The two principal peaks common to all functions, indicated by red and blue shading, can be assigned to the two types of Ca2+-ion pair illustrated in d.
Coarse graining
In seeking to improve our understanding of the structure of ACC, we focused on the Ca-pair correlation function gCa(r)—after all, this is the contribution to the pair distribution function that exhibits the strongest persistent well-defined oscillations. In Fig. 2e, we show this function as extracted from our HRMC configurations compared against that reported in the RMC study of ref. 14. We also include the normalized Fourier transform of the experimental FX(Q) function; this transform is an approximate (total) pair distribution function that emphasizes contributions from Ca–Ca pairs as a consequence of the larger X-ray scattering cross-section for Ca relative to C, O and H. Although all three real-space correlation functions show maxima at r ≈ 4 and 6 Å, it is the HRMC result that resolves these features most clearly. By counting Ca–Ca pairs separated by Ca–O–Ca and Ca–O–C–O–Ca pathways in our HRMC configuration, we confirmed that the two maxima in gCa(r) occur at the preferred Ca⋯Ca distances associated with these two different carbonate bridging motifs (Extended Data Fig. 3). Indeed these same preferred separations recur among crystalline calcium carbonates, as noted in ref. 14.
Access to a smoothly varying measure of gCa(r), together with the HRMC configurations from which it is calculated, allowed us to exploit a recently developed approach for the direct measurement of effective pair potentials from particle-coordinate data16. The method works by equating the pair distribution functions measured directly, on the one hand, and calculated using a test-particle insertion approach29,30, on the other31. Applying this methodology to the atomic coordinates in our HRMC-refined model, we extracted the effective Ca2+-ion pair potential uCa(r) shown in Fig. 3a. This function has two distinct potential wells, the minima of which are centred near distances for which gCa(r) has its maxima. The physical meaning of uCa(r) is that it captures the effective two-body interactions between Ca–Ca pairs, mediated by carbonate and water, as required to account for the observed gCa(r). That this interaction energy is minimized when Ca–Ca pairs are separated by distances corresponding to either Ca–O–Ca or Ca–O–C–O–Ca pathways makes intuitive sense (of course); the longer (6 Å) separation appears energetically more favourable, probably because it minimizes the electrostatic repulsion between calcium ions bound to a common carbonate.
a, The effective Ca⋯Ca interatomic potential extracted from our HRMC configurations16 (open circles) and least-squares fit using a modified LJG model (line) as described in the text. The inset shows the orientational correlation functions (equation (1)), which vanish for distances relevant to the Ca⋯Ca separations. In the lower panel, the yellow dashed line corresponds to the additional broad, repulsive Gaussian term. b, Representative MC configuration of Ca atoms (beige spheres) generated by the LJG potential, parameterized by the fit shown in a. The Ca atoms are not uniformly distributed, but cluster to leave Ca-poor voids, shown as aquamarine surfaces. Note the qualitative similarity to the heterogeneous structure of ACC represented in Fig. 1c. c, Approximate location of ACC effective LJG parameters (star) in the LJG phase space as reported in ref. 11; shaded regions correspond to the stability fields of different ground-state structures, and solid lines denote the approximate locations of phase boundaries.
One assumption in using an isotropic effective pair potential to capture interactions mediated by anisotropic molecular species, such as H2O and CO32−, is that any local anisotropy is sufficiently short-ranged. We checked this point by calculating from our original (all-atom) HRMC configurations the orientational correlation functions:
where P2(x) is the second-order Legendre polynomial, and S are vectors parallel to a suitable local axis (for example, C3, C2) of molecules separated by distance r (ref. 32). We find that ϕ(r) is essentially featureless—for both carbonate and water—for all but the very shortest intermolecular approaches, which occur for distances smaller than the nearest-neighbour Ca⋯Ca separation (Fig. 3a, inset). Accordingly, the anisotropy of individual molecules is relevant only at a length scale smaller than that over which the effective interactions between Ca2+-ion pairs operate. The double-well form of uCa(r) is important for a number of reasons. First, it explains why simple hard-sphere or LJ potentials fail to reproduce the experimental gCa(r): if tuned to capture the 4 Å nearest-neighbour correlation, such potentials predict a second maximum just below 8 Å that is not observed in experiments. Second, it allows us to rationalize the inability of earlier EPSR studies to determine the correct Ca distribution function; for example, the study of ref. 20 included an LJ parameterization of Ca⋯Ca interactions that then resulted in a gCa(r) function with maxima at positions clearly inconsistent with the inverse Fourier transform of the experimental FX(Q). Third, multi-well potentials are well known to support very complex phase behaviour9,11,12,33,34,35, suggesting a qualitative explanation of the complexity of ACC.
LJG parameterization
To test this hypothesis of a link between effective potential and structural complexity, we sought to map uCa(r) onto a suitable multi-well potential for which the corresponding theory is already well established. We found that a double-well LJG interaction8 described the observed functional form surprisingly well, as long as we included an additional broad, repulsive Gaussian term that helps capture the local maxima between and beyond the two minima of the LJG function. The behaviour of the LJG potential is characterized by three parameters—ε, r0 and σ—which describe, respectively, the depth, position and width of the Gaussian well relative to the LJ component9,11. A least-squares fit to uCa(r) gave the values ε = 4.1, r0 = 1.4 and σ = 0.14 (Fig. 3a); note that r0 is particularly well defined because it is closely related to the ratio of the Ca⋯Ca separations resulting from the two different carbonate bridging motifs (~6 Å and 4 Å). We will return to the importance of these empirical parameters in due course. We note, in passing, related work on the description of coarse-grained molecular systems with double-well potentials, where one minimum is explicitly assigned to enthalpic and one to entropic terms36, and on the ‘learning’ of effective pair potentials from simulation data by back-propagation37.
As a simple check that our combination of g(r) inversion and potential parameter fitting does indeed result in a meaningful effective pair potential, we carried out direct MC simulations driven by our parameterized LJG potential. These simulations were performed using the experimentally determined Ca particle density in ACC, and although we focus here on MC simulations (for fairest comparison with HRMC), the same results emerge if we use MD instead (Methods and Extended Data Fig. 5). The corresponding pair correlation function closely matches our HRMC gCa(r), as expected (Fig. 2e), and the resulting structure resembles the Ca distribution in the fully atomistic model (Fig. 3b; cf. Fig. 1c). But the similarity between coarse-grained LJG-driven and HRMC Ca distributions turns out to extend beyond pair correlations, and we explore this more extensive similarity in various forms (for example, ring statistics, Voronoi volume distributions and higher-order correlation functions) in Supplementary Figs. 2–4 and Supplementary Discussion 4. A particular point of interest is that the MC configurations contain Ca-rich/-poor regions that are qualitatively similar to those observed in the original atomistic model (Fig. 3b)—the clear implication being that, at the density of ACC, an inhomogeneous Ca distribution is encoded within the effective Ca⋯Ca interaction itself.
Discussion
From the perspective of soft-matter theory, much of the interest in the LJG potential lies in the complexity of phase behaviour that it supports9,11,12,38. This complexity arises because of competition between the structure-directing effects of LJ and Gaussian components, which operate at different length scales. When the positions of the LJ and Gaussian minima are related by a factor 1.2 ≤ r0 ≤ 1.6, there is particularly strong geometric frustration that results in a general resistance to crystallization9 and the emergence of many competing low-symmetry ground-state structures11. This behaviour extends across a wide variety of relative well depths ε ≥ 1 for the corresponding relative Gaussian width σ = 0.14 (ref. 11). Hence the empirical parameters we have determined to be relevant to effective Ca⋯Ca interactions in ACC—that is, r0 = 1.4, ε = 4.1 and σ = 0.14—locate the system in one of the most complicated parts of the LJG phase diagram (Fig. 3c)11. In developing this mapping onto the LJG model, we assume that the additional broad Gaussian term we have included in our parameterization does not strongly influence the phase behaviour (note that the value of r0 does not vary substantially if it is omitted from our fit). Similarly, we cannot be certain of the effects of finite temperature and fixed density on LJG phase behaviour, as these have not yet been studied from theory. It is nevertheless a general phenomenon in frustrated systems that regions of strong geometric frustration are characterized by the existence of many competing ground states with suppressed ordering temperatures, above which the system is disordered but far from random39,40.
In the context of ACC, the implications are twofold. First, the different favoured Ca⋯Ca separations for carbonate-bridged Ca pairs—that is, 4 and 6 Å—are configurationally difficult to satisfy in a three-dimensionally periodic (that is, crystalline) structure with the density of ACC and in the absence of anisotropic interactions. This rationalizes, in general terms, why an amorphous form of hydrated CaCO3 is so readily accessible. Second, the sensitivity of the LJG potential around r0 = 1.4 hints—again in general terms—at why ACC might be directed to crystallize into a number of different polymorphs. Of course, as the water content of ACC varies during ageing of the material, both the effective Ca⋯Ca interactions and the bulk density must change, which makes extrapolation from the LJG effective potential of ACC difficult. Increased material density also strengthens the orientational correlations in molecular components, and so one expects the isotropic effective pair potential description to break down as crystallization is approached. Nevertheless, at the density of ACC and in the absence of orientational order, the occurrence of an amorphous state is now more easily rationalized. Furthermore, the incorporation of Mg2+ or PO43− ions into ACC will introduce statistical variations into the effective potential governing cation arrangements, favouring further the amorphous state—much as magnetic exchange disorder can stabilize spin glasses41.
Whereas the (hitherto unsuccessful) search for ‘real-world’ materials governed by isotropic multi-well potentials has focused on the atomic (alloys) and mesoscopic (colloids) length scales11,12, our study of ACC suggests that the intermediate domain of nanoscale materials may in fact be a more fertile source of relevant examples. By their very nature, molecular ions tend to exhibit a range of coordination modes, which must give rise to multiple specific preferred distances between the counterions they coordinate. Whenever these distances are geometrically frustrated, as in ACC, one expects that the corresponding effective potential must contain multiple wells so as to stabilize both separations at once. Through suitable choice of chemical components, one might hope to navigate the complicated phase space associated with such unconventional potentials. Doing so will provide an important test of theory, on the one hand, and also allow the targeted design of complex structures through self-assembly, on the other.
Our coarse-grained approach to understanding ACC structure may be applicable to other poorly ordered inorganic solids of particular scientific importance. Amorphous calcium phosphate (the precursor to bone) and calcium–silicate–hydrates (that is, Portland cements) are obvious ever-contentious examples42,43 where one might expect the different bridging motifs—now of the phosphate or (poly)silicate anions—to again moderate an effective interaction potential with multiple minima. Better understanding the structures of long-studied materials is certainly one fruitful avenue for future research, but our work also suggests an alternative pathway towards complex materials design. By varying the inorganic cation radius for a given molecular counterion, or by changing the degree of hydration, one might hope to control the ratio of the distances at which minima in the effective potential occur. What emerges is a strategy of ‘interaction engineering’ to target a particular phase of interest, or to stabilize or destabilize an amorphous form of matter.
Methods
HRMC refinements
Our approach to carrying out HRMC refinements was modelled closely on the previous RMC refinements of ref. 14, which were carried out using the RMCProfile code44. For the present study we used a related custom code, written in Python. The X-ray scattering calculations carried out by this code were exactly those employed by RMCProfile, but the code was also able to interface with potential-energy evaluations carried out using the LAMMPS software45. The custom Python code imports functionality from the following packages: PyLammpsMPI46, Numba47 and ASE48.
Starting configurations were generated in the following manner. We began by placing 1,620 Ca atoms randomly in a box of dimensions 52.8 × 54.8 × 45.2 Å3—this being the same box size as used in ref. 14. An initial energy minimization was carried out with a repulsive potential between Ca atoms (an LJ functional form, truncated at the zero-crossing distance), so as to prevent any Ca–Ca distances of <3.0 Å. To this homogeneous distribution of Ca atoms we added a stoichiometric number of rigid carbonate and water molecules with idealized geometries. Carbonate molecules were fixed to adopt a C–O bond length of rCO = 1.284 Å—as observed in calcite and as defined for the relevant CaCO3 potential18. Water molecules were treated using the four-site rigid model, TIP4P-Ew49, which uses a fixed geometry of the water molecule (O–H bond length rOH = 0.9572 Å, H–O–H bond angle θHOH = 104.52°). Short-range repulsive terms (as described above) were applied between the rigid bodies to prevent close contacts during a subsequent energy minimization and a short NVT-ensemble MD run, aiming to achieve a homogeneous distribution of particles (cf. the method of ref. 50).
The HRMC cost function, to be optimized during refinement, was defined as
where
represents the mismatch between calculated and experimental Q-weighted X-ray total scattering functions QF(Q) (ref. 51), and E is the configurational energy as obtained from the empirical potential. The experimental QF(Q) data were those reported in ref. 13 and ref. 14, which span the range of momentum transfers 1.2 ≤ Q ≤ 25.0 Å−1. The corresponding HRMC QF(Q) function was computed by weighted Fourier transform of the partial pair correlation functions, gij(r) (refs. 44,51), themselves obtained as histograms with a bin width of Δr = 0.02 Å. Total-scattering calculations were parallelized using the package Numba, a just-in-time compiler for Python47. The value of E was determined using the rigid-body force field for aqueous calcium carbonate of ref. 18, with the corresponding calculation delegated to the LAMMPS software45 via the PyLammpsMPI parallel LAMMPS–Python interface46. The simulation temperature was set to T = 300 K.
The parameter σ in equation (3) controls the relative weights of fit-to-data and potential energies in the overall HRMC cost function, and its value must be determined empirically. Through systematic tests of the variation in \({\chi }_{QF(Q)}^{2}\) and E with σ, we determined the value σ = 0.057 to provide the most appropriate balance in this case.
Individual moves were proposed and accepted or rejected according to the usual Metropolis–Hastings criterion. These moves involved a combination of atomic displacements (maximum value 0.1 Å) and rigid-body translations or rotations (maximum values of 0.1 Å and 1°, respectively) of carbonate and water molecules. In contrast to the RMC study of ref. 14, no closest-approach constraints were employed. The incorporation of interatomic potentials within the HRMC cost function ensured that such constraints were unnecessary.
HRMC refinements were continued until the values of χ2 and E were deemed to have converged (Extended Data Fig. 1).
MD simulations
MD simulations were performed using LAMMPS45 in the NVT ensemble at 300 K, with a Nosé–Hoover thermostat controlling the temperature. The time step was 1 fs with a relaxation time of 0.1 ps for temperature control (cf. the ACC MD simulations in refs. 27,52). We tested the stability of our HRMC ACC structural model by carrying out a 1-ns MD simulation (one million time steps) starting from the final HRMC configuration. The simulation was stable with respect to NVT MD (Extended Data Fig. 1), by which we mean that no substantial structural reorganization occurred.
As anticipated, the HRMC configuration is indeed a compromise between fit-to-data and energy minimization. During the MD simulation, it quickly decreased in energy by ~0.3 eV per Ca before reaching thermal equilibrium (Extended Data Fig. 1). The negative pressure (Extended Data Fig. 1) indicates that the system is driven towards a more compact atomic arrangement than implied by the experimental density. An MD simulation performed in the NPT ensemble led to an increase in density from 2.43 to 2.91 g cm−3.
Pair distribution function inversion
The test-particle pair distribution function inversion method was carried out using the code described in ref. 30, modified for application to a three-dimensional system. The Ca coordinates and the averaged gCa(r) (up to a cutoff of 12 Å with a bin size of Δr = 0.2 Å) from the final 12 frames of the HRMC trajectory were used as input for the inversion algorithm. Approximately 10,000 trial insertions were used per configuration, so as to satisfy convergence criteria.
Coarse-grained simulations
MC and NVT MD simulations were performed using a custom Python program with potential-energy evaluations and MD protocols carried out using the LAMMPS software45.
Twelve starting configurations for each method (24 in total) were generated by randomly placing 1,620 Ca atoms in a box with identical cell dimensions as the HRMC configuration (52.8 × 54.8 × 45.2 Å3). The simulation temperature was set to T = 300 K (cf. HRMC simulations). For MC simulations, the maximum atomic displacement was 0.1 Å. MC simulations were terminated after four million moves were accepted, at which point convergence with respect to the ensemble energy was met (Extended Data Fig. 5). An initial energy minimization (using the the conjugate-gradient algorithm for 100 steps) was performed for the starting MD configurations to prevent close contacts rendering the simulation unstable. This gave an average minimum energy of −0.03028 ± 0.00090 eV per Ca. The MD simulations were then run in the NVT ensemble for 1 ns, with a 0.5-fs time step and 50-fs temperature damping constant.
Data availability
Data supporting the findings of this study are available within the paper and its Supplementary Information files, or at https://doi.org/10.5281/zenodo.8238547. Source data are provided with this paper.
Code availability
All custom code used in this study was developed using widely available algorithms. A copy of the Python scripts used to carry out the HRMC refinements is included as Supplementary Code 1.
References
Gebauer, D., Völkel, A. & Cölfen, H. Stable prenucleation calcium carbonate clusters. Science 322, 1819–1822 (2008).
Aizenberg, J., Lambert, G., Weiner, S. & Addadi, L. Factors involved in the formation of amorphous and crystalline calcium carbonate: a study of an ascidian skeleton. J. Am. Chem. Soc. 124, 32–39 (2002).
Raz, S., Hamilton, P. C., Wilt, F. H., Weiner, S. & Addadi, L. The transient phase of amorphous calcium carbonate in sea urchin larval spicules: the involvement of proteins and magnesium ions in its formation and stabilization. Adv. Funct. Mater. 13, 480–486 (2003).
Aizenberg, J. Crystallization in patterns: a bio-inspired approach. Adv. Mater. 16, 1295–1302 (2004).
Addadi, L., Raz, S. & Weiner, S. Taking advantage of disorder: amorphous calcium carbonate and its roles in biomineralization. Adv. Mater. 15, 959–970 (2003).
Weiner, S., Sagi, I. & Addadi, L. Structural biology. Choosing the crystallization path less traveled. Science 309, 1027–1028 (2005).
Beniash, E., Aizenberg, J., Addadi, L. & Weiner, S. Amorphous calcium carbonate transforms into calcite during sea urchin larval spicule growth. Proc. R. Soc. Lond. B 264, 461–465 (1997).
Rechtsman, M., Stillinger, F. & Torquato, S. Designed interaction potentials via inverse methods for self-assembly. Phys. Rev. E 73, 011406 (2006).
Engel, M. & Trebin, H.-R. Structural complexity in monodisperse systems of isotropic particles. Z. Kristallogr. 223, 721–725 (2008).
Jain, A., Errington, J. R. & Truskett, T. M. Dimensionality and design of isotropic interactions that stabilize honeycomb, square, simple cubic and diamond lattices. Phys. Rev. X 4, 031049 (2014).
Dshemuchadse, J., Damasceno, P. F., Phillips, C. L., Engel, M. & Glotzer, S. C. Moving beyond the constraints of chemistry via crystal structure discovery with isotropic multiwell pair potentials. Proc. Natl Acad. Sci. USA 118, e2024034118 (2021).
Engel, M. & Trebin, H.-R. Self-assembly of monatomic complex crystals and quasicrystals with a double-well interaction potential. Phys. Rev. Lett. 98, 225505 (2007).
Michel, F. M. et al. Structural characteristics of synthetic amorphous calcium carbonate. Chem. Mater. 20, 4720–4728 (2008).
Goodwin, A. L. et al. Nanoporous structure and medium-range order in synthetic amorphous calcium carbonate. Chem. Mater. 22, 3197–3205 (2010).
Opletal, G. et al. Hybrid approach for generating realistic amorphous carbon structure using metropolis and reverse Monte Carlo. Mol. Simul. 28, 927–938 (2002).
Stones, A. E., Dullens, R. P. A. & Aarts, D. G. A. L. Model-free measurement of the pair potential in colloidal fluids using optical microscopy. Phys. Rev. Lett. 123, 098002 (2019).
McGreevy, R. L. & Pusztai, L. Reverse Monte Carlo simulation: a new technique for the determination of disordered structures. Mol. Simul. 1, 359–367 (1988).
Raiteri, P., Gale, J. D., Quigley, D. & Rodger, P. M. Derivation of an accurate force-field for simulating the growth of calcium carbonate from aqueous solution: a new model for the calcite–water interface. J. Phys. Chem. C 114, 5997–6010 (2010).
Reeder, R. J. et al. Characterization of structure in biogenic amorphous calcium carbonate: pair distribution function and nuclear magnetic resonance studies of lobster gastrolith. Cryst. Growth Des. 13, 1905–1914 (2013).
Cobourne, G. et al. Neutron and X-ray diffraction and empirical structure refinement modelling of magnesium stabilised amorphous calcium carbonate. J. Non-Cryst. Sol. 401, 154–158 (2014).
Wang, H.-W. et al. Synthesis and structure of synthetically pure and deuterated amorphous (basic) calcium carbonates. Chem. Commun. 53, 2942–2945 (2017).
Jensen, A. C. S. et al. Hydrogen bonding in amorphous calcium carbonate and molecular reorientation induced by dehydration. J. Phys. Chem. C 122, 3591–3598 (2018).
Demichelis, R., Raiteri, P., Gale, J. D., Quigley, D. & Gebauer, D. Stable prenucleation mineral clusters are liquid-like ionic polymers. Nat. Commun. 2, 590 (2011).
Ihli, J. et al. Dehydration and crystallization of amorphous calcium carbonate in solution and in air. Nat. Commun. 5, 3169 (2014).
Nebel, H., Neumann, M., Mayer, C. & Epple, M. On the structure of amorphous calcium carbonate—a detailed study by solid-state NMR spectroscopy. Inorg. Chem. 47, 7874–7879 (2008).
Goodwin, A. L. Opportunities and challenges in understanding complex functional materials. Nat. Commun. 10, 4461 (2019).
Singer, J. W., Yazaydin, A. Ö., Kirkpatrick, R. J. & Bowers, G. M. Structure and transformation of amorphous calcium carbonate: a solid-state 43Ca NMR and computational molecular dynamics investigation. Chem. Mater. 24, 1828–1836 (2012).
Clark, S. M. et al. The nano- and meso-scale structure of amorphous calcium carbonate. Sci. Rep. 12, 6870 (2022).
Henderson, J. R. On the test particle approach to the statistical mechanics of fluids. Hard sphere fluid. Mol. Phys. 48, 389–400 (1983).
Stones, A. E., Dullens, R. P. A. & Aarts, D. G. A. L. Contact values of pair distribution functions in colloidal hard disks by test-particle insertion. J. Chem. Phys. 148, 241102 (2018).
Widom, B. Some topics in the theory of fluids. J. Chem. Phys. 39, 2808–2812 (1963).
Cinacchi, G. & Torquato, S. Hard convex lens-shaped particles: characterization of dense disordered packings. Phys. Rev. E 100, 062902 (2019).
Elenius, M., Zetterling, F. H. M., Dzugutov, M., Fredrickson, D. C. & Lidin, S. Structural model for octagonal quasicrystals derived from octagonal symmetry elements arising in β-Mn crystallization of a simple monatomic liquid. Phys. Rev. B 79, 144201 (2009).
Mihalkovič, M. & Henley, C. L. Empirical oscillating potentials for alloys from ab initio fits and the prediction of quasicrystal-related structures in the Al-Cu-Sc system. Phys. Rev. B 85, 092102 (2012).
Zhou, P., Proctor, J. C., van Anders, G. & Glotzer, S. C. Alchemical molecular dynamics for inverse design. Mol. Phys. 117, 3968–3980 (2019).
Pretti, E. & Shell, M. S. A microcanonical approach to temperature-transferable coarse-grained models using the relative entropy. J. Chem. Phys. 155, 094102 (2021).
Wang, W., Wu, Z., Dietschreit, J. C. B. & Gómez-Bombarelli, R. Learning pair potentials using differentiable simulations. J. Chem. Phys. 158, 044113 (2023).
Suematsu, A., Yoshimori, A., Saiki, M., Matsui, J. & Odagaki, T. Control of solid-phase stability by interaction potential with two minima. J. Mol. Liq. 200, 12–15 (2014).
Ziman, J. M. Models of Disorder. The Theoretical Physics of Homogeneously Disordered Systems (Cambridge Univ. Press, 1979).
Moessner, R. & Ramirez, A. P. Geometrical frustration. Phys. Today 59, 24–29 (2006).
Saunders, T. E. & Chalker, J. T. Spin freezing in geometrically frustrated antiferromagnets with weak disorder. Phys. Rev. Lett. 98, 157201 (2007).
Lowenstam, H. A. & Weiner, S. Transformation of amorphous calcium phosphate to crystalline dahllite in the radular teeth of chitons. Science 227, 51–53 (1985).
Richardson, I. G. Model structures for C-(A)-S-H(I). Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater 70, 903–923 (2014).
Tucker, M. G., Keen, D. A., Dove, M. T., Goodwin, A. L. & Hui, Q. RMCProfile: reverse Monte Carlo for polycrystalline materials. J. Phys. Condens. Matter 19, 335218 (2007).
Thompson, A. P. et al. LAMMPS—a flexible simulation tool for particle-based materials modeling at the atomic, meso and continuum scales. Comput. Phys. Commun. 271, 108171 (2022).
Janssen, J. PyLammpsMPI (version 0.0.8). GitHub https://github.com/pyiron/pylammpsmpi (2022).
Lam, S. K., Pitrou, A. & Seibert, S. Numba: a LLVM-based Python JIT compiler. In Proc. Second Workshop on the LLVM Compiler Infrastructure in HPC, LLVM ‘15, Vol. 7, 1–6 (Association for Computing Machinery, 2015).
Larsen, A. H. et al. The Atomic Simulation Environment—a Python library for working with atoms. J. Phys. Condens. Matter 29, 273002 (2017).
Horn, H. W. et al. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 120, 9665–9678 (2004).
Bushuev, Y. G., Finney, A. R. & Rodger, P. M. Stability and structure of hydrated amorphous calcium carbonate. Cryst. Growth Des. 15, 5269–5279 (2015).
Keen, D. A. A comparison of various commonly used correlation functions for describing total scattering. J. Appl. Crystallogr. 34, 172–177 (2001).
Saharay, M. & Kirkpatrick, R. J. Water dynamics in hydrated amorphous materials: a molecular dynamics study of the effects of dehydration in amorphous calcium carbonate. Phys. Chem. Chem. Phys. 19, 29594–29600 (2017).
Acknowledgements
T.C.N. was supported through an Engineering and Physical Sciences Research Council DTP award (grant no. EP/T517811/1). A.E.S. acknowledges financial support from the University of Oxford Clarendon Fund. A.L.G. acknowledges useful discussions with M. T. Dove (QMUL) and financial support from the ERC (grant no. 788144). F.M.M. acknowledges financial support provided by the National Science Foundation through CAREER-1652237 and the Virginia Tech National Center for Earth and Environmental Nanotechnology Infrastructure (‘NanoEarth’, NSF Cooperative Agreement 1542100). This research used resources of the Advanced Photon Source, a US Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under contract no. DE-AC02-06CH11357. We acknowledge use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out this work (https://doi.org/10.5281/zenodo.22558).
Author information
Authors and Affiliations
Contributions
T.C.N. carried out the hybrid reverse Monte Carlo refinements and molecular dynamics simulations, under the supervision of V.L.D. and A.L.G., building on a preliminary investigation performed with A.P. These refinements made use of X-ray total scattering data collected and normalized by F.M.M. and R.J.R. T.C.N. performed the effective pair-potential determination, using an algorithm developed by A.E.S. and D.G.A.L.A., and coded by A.E.S. T.C.N., V.L.D. and A.L.G. analysed the data and developed the main conclusions regarding interpretation of the structure of amorphous calcium carbonate. All authors contributed to discussions. T.C.N., V.L.D. and A.L.G. drafted the paper, and all authors contributed to its final version.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Chemistry thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Evolution of system properties during HRMC refinement and MD simulation.
a The cost function relating to the X-ray scattering data during HRMC refinement. b The change in potential energy of the simulated structural model during HRMC refinement (black) and subsequent MD simulation (red). Energies are reported relative to that obtained in equivalent NVT MD simulations of the crystalline monohydrocalcite polymorph of CaCO3.H2O. The c temperature, d pressure, and e mean-squared displacement (MSD) of atoms during the HRMC MD simulation, respectively.
Extended Data Fig. 2 Partial pair distribution functions extracted from the HRMC ACC model.
Each partial pair distribution function (PDF) is calculated with a bin width of Δr = 0.02 Å, averaged over 12 HRMC trajectory configurations exported in intervals of 100,000 proposed moves. Sharp features arise from rigid-body correlations (light grey). For the relevant partial PDFs we omit rigid-body terms contributions from the data shown in black.
Extended Data Fig. 3 Key bond-length and bond-angle distributions in the HRMC ACC model.
a The bond-length distributions for Ca-O divided into Ca-OC and Ca-OW contributions. The average Ca-OC bond length (2.5(1) Å) is shifted to larger r values relative to the average Ca-OW bond length (2.3(1) Å). b The interatomic distance between calcium atoms bound to the same carbonate can be divided into those which share a common oxygen atom and those which are connected via the carbonate molecule. These two coordination interactions give rise to the characteristic geometric frustration observed for ACC. c Bond-angle distributions for OC-Ca-OC triplets, decomposed into mono- and bidentate coordination modes. The bidentate coordination mode gives rise to a sharp peak centred at 50∘. d OW-Ca-O bond-angle distributions. The lower relative intensity of OW-Ca-OW correlations reflects the low likelihood of finding multiple water molecules bound to the same calcium atom. For each panel, the plots at the top show the corresponding cumulative distribution functions.
Extended Data Fig. 4 Characteristics of water distribution in the HRMC ACC model.
a Radial distribution functions for neighbours of carbonate oxygen atoms in the structure. b Radial distribution functions for neighbours of oxygen atoms in water molecules (‘OW’) only. Intramolecular correlations are omitted for clarity. c The distribution of cluster sizes for those water molecules that do not take part in the percolating water network. A cluster size of 1 means an isolated water molecule that is not within reach of any others according to the defined cutoff distances (see Supplementary Table 1).
Extended Data Fig. 5 Evolution of coarse-grained simulation ensemble energies.
The energy of each ensemble, relative to the minimum configuration energy across all trajectories, as a function of a accepted MC moves, and b MD simulation time. Each of the 12 trajectories is given a different colour. This initial sharp decrease and subsequent increase in Erel for the MD configurations arises from the initially randomised particle positions, followed by a short energy minimisation, before beginning the NVT MD run.
Supplementary information
Supplementary Information
Supplementary Figs. 1–4, Table 1, Discussions 1–4 and references.
Supplementary Data 1
Atomic coordinates in crystallographic information file format for a representative hybrid reverse Monte Carlo model of amorphous calcium carbonate.
Supplementary Data 2
Atomic coordinates in crystallographic information file format for a representative reverse Monte Carlo model of amorphous calcium carbonate.
Supplementary Data 3
Atomic coordinates in crystallographic information file format for a representative Molecular Dynamics model of amorphous calcium carbonate.
Supplementary Data 4
Atomic coordinates in crystallographic information file format for a representative coarse-grained Lennard-Jones–Gauss model of calcium arrangements in amorphous calcium carbonate.
Supplementary Code 1
Python scripts used to carry out HRMC refinements as discussed in the main text.
Source data
Source Data Fig. 1
Statistical source data.
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nicholas, T.C., Stones, A.E., Patel, A. et al. Geometrically frustrated interactions drive structural complexity in amorphous calcium carbonate. Nat. Chem. 16, 36–41 (2024). https://doi.org/10.1038/s41557-023-01339-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41557-023-01339-2
This article is cited by
-
Isotropic models for anisotropic inorganics
Nature Chemistry (2024)