Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Quantum interference effects elucidate triplet-pair formation dynamics in intramolecular singlet-fission molecules

Nature Chemistry volume 15, pages 339–346 (2023)Cite this article

Subjects

Abstract

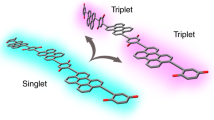
Quantum interference (QI)—the constructive or destructive interference of conduction pathways through molecular orbitals—plays a fundamental role in enhancing or suppressing charge and spin transport in organic molecular electronics. Graphical models were developed to predict constructive versus destructive interference in polyaromatic hydrocarbons and have successfully estimated the large conductivity differences observed in single-molecule transport measurements. A major challenge lies in extending these models to excitonic (photoexcited) processes, which typically involve distinct orbitals with different symmetries. Here we investigate how QI models can be applied as bridging moieties in intramolecular singlet-fission compounds to predict relative rates of triplet pair formation. In a series of bridged intramolecular singlet-fission dimers, we found that destructive QI always leads to a slower triplet pair formation across different bridge lengths and geometries. A combined experimental and theoretical approach reveals the critical considerations of bridge topology and frontier molecular orbital energies in applying QI conductance principles to predict rates of multiexciton generation.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Model systems designed to investigate the role of QI.
Fig. 2: Determination of the time constants for triplet pair formation.
Fig. 3: Comparison of SF rates (normalized to the largest kSF) across all Ph, N and A bridges in this work.
Fig. 4: Contributions to the absorption spectra from the CT wavefunctions that mediate fast SF.

Similar content being viewed by others

Data availability

The raw transient absorption data used to generate Figs. 2 and 3 and the corresponding analysis are freely available via the Dryad public repository: https://doi.org/10.5061/dryad.x95x69pnn. Additional data are available upon request. Source data are provided with this paper.

References

  1. Su, T. A., Neupane, M., Steigerwald, M. L., Venkataraman, L. & Nuckolls, C. Chemical principles of single-molecule electronics. Nat. Rev. Mater. 1, 16002 (2016).

    Article  CAS  Google Scholar 

  2. Lambert, C. J. Basic concepts of quantum interference and electron transport in single-molecule electronics. Chem. Soc. Rev. 44, 875–888 (2015).

    Article  CAS  PubMed  Google Scholar 

  3. Jan van der Molen, S. & Liljeroth, P. Charge transport through molecular switches. J. Phys. Condens. Matter 22, 133001 (2010).

    Article  Google Scholar 

  4. Guédon, C. M. et al. Observation of quantum interference in molecular charge transport. Nat. Nanotechnol. 7, 305–309 (2012).

    Article  PubMed  Google Scholar 

  5. Arroyo, C. R. et al. Signatures of quantum interference effects on charge transport through a single benzene ring. Angew. Chem. Int. Ed. 52, 3152–3155 (2013).

    Article  CAS  Google Scholar 

  6. Solomon, G. C. et al. Understanding quantum interference in coherent molecular conduction. J. Chem. Phys. 129, 054701 (2008).

    Article  PubMed  Google Scholar 

  7. Tsuji, Y., Hoffmann, R., Strange, M. & Solomon, G. C. Close relation between quantum interference in molecular conductance and diradical existence. Proc. Natl Acad. Sci. USA 113, E413–E419 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  8. Markussen, T., Stadler, R. & Thygesen, K. S. The relation between structure and quantum interference in single molecule junctions. Nano Lett. 10, 4260–4265 (2010).

    Article  CAS  PubMed  Google Scholar 

  9. Ortiz, R. et al. Exchange rules for diradical π-conjugated hydrocarbons. Nano Lett. 19, 5991–5997 (2019).

    Article  CAS  PubMed  Google Scholar 

  10. Gorczak, N. et al. Computational design of donor–bridge–acceptor systems exhibiting pronounced quantum interference effects. Phys. Chem. Chem. Phys. 18, 6773–6779 (2016).

    Article  CAS  PubMed  Google Scholar 

  11. Gorczak, N. et al. Charge transfer versus molecular conductance: molecular orbital symmetry turns quantum interference rules upside down. Chem. Sci. 6, 4196–4206 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  12. Sanders, S. N. et al. Exciton correlations in intramolecular singlet fission. J. Am. Chem. Soc. 138, 7289–7297 (2016).

    Article  CAS  PubMed  Google Scholar 

  13. Pun, A. B. et al. Ultra-fast intramolecular singlet fission to persistent multiexcitons by molecular design. Nat. Chem. 11, 821–828 (2019).

    Article  CAS  PubMed  Google Scholar 

  14. Krishnapriya, K. C. et al. Spin density encodes intramolecular singlet exciton fission in pentacene dimers. Nat. Commun. 10, 33 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  15. Hetzer, C., Guldi, D. M. & Tykwinski, R. R. Pentacene dimers as a critical tool for the investigation of intramolecular singlet fission. Chem. Eur. J. 24, 8245–8257 (2018).

    Article  CAS  PubMed  Google Scholar 

  16. Basel, B. S. et al. Influence of the heavy-atom effect on singlet fission: a study of platinum-bridged pentacene dimers. Chem. Sci. 10, 11130–11140 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  17. Margulies, E. A. et al. Enabling singlet fission by controlling intramolecular charge transfer in π-stacked covalent terrylenediimide dimers. Nat. Chem. 8, 1120–1125 (2016).

    Article  CAS  PubMed  Google Scholar 

  18. Sakuma, T. et al. Long-lived triplet excited states of bent-shaped pentacene dimers by intramolecular singlet fission. J. Phys. Chem. A 120, 1867–1875 (2016).

    Article  CAS  PubMed  Google Scholar 

  19. Nakamura, S. et al. Enthalpy–entropy compensation effect for triplet pair dissociation of intramolecular singlet fission in phenylene spacer-bridged hexacene dimers. J. Phys. Chem. Lett. 12, 6457–6463 (2021).

    Article  CAS  PubMed  Google Scholar 

  20. Korovina, N. V. et al. Linker-dependent singlet fission in tetracene dimers. J. Am. Chem. Soc. 140, 10179–10190 (2018).

    Article  CAS  PubMed  Google Scholar 

  21. Ito, S., Nagami, T. & Nakano, M. Design principles of electronic couplings for intramolecular singlet fission in covalently-linked systems. J. Phys. Chem. A 120, 6236–6241 (2016).

    Article  CAS  PubMed  Google Scholar 

  22. Paul, S., Govind, C. & Karunakaran, V. Planarity and length of the bridge control rate and efficiency of intramolecular singlet fission in pentacene dimers. J. Phys. Chem. B 125, 231–239 (2021).

    Article  CAS  PubMed  Google Scholar 

  23. Abraham, V. & Mayhall, N. J. Revealing the contest between triplet–triplet exchange and triplet–triplet energy transfer coupling in correlated triplet pair states in singlet fission. J. Phys. Chem. Lett. 12, 10505–10514 (2021).

    Article  CAS  PubMed  Google Scholar 

  24. Abraham, V. & Mayhall, N. J. Simple rule to predict boundedness of multiexciton states in covalently linked singlet-fission dimers. J. Phys. Chem. Lett. 8, 5472–5478 (2017).

    Article  CAS  PubMed  Google Scholar 

  25. Chesler, R., Khan, S. & Mazumdar, S. Wave function based analysis of dynamics versus yield of free triplets in intramolecular singlet fission. J. Phys. Chem. A 124, 10091–10099 (2020).

    Article  CAS  PubMed  Google Scholar 

  26. Herrmann, C. Electronic communication as a transferable property of molecular bridges? J. Phys. Chem. A 123, 10205–10223 (2019).

    Article  CAS  PubMed  Google Scholar 

  27. Walter, D., Neuhauser, D. & Baer, R. Quantum interference in polycyclic hydrocarbon molecular wires. Chem. Phys. 299, 139–145 (2004).

    Article  CAS  Google Scholar 

  28. Bajaj, A., Kaur, P., Sud, A., Berritta, M. & Ali, Md. E. Anomalous effect of quantum interference in organic spin filters. J. Phys. Chem. C 124, 24361–24371 (2020).

    Article  CAS  Google Scholar 

  29. Sanders, S. N. et al. Quantitative intramolecular singlet fission in bipentacenes. J. Am. Chem. Soc. 137, 8965–8972 (2015).

    Article  CAS  PubMed  Google Scholar 

  30. Parenti, K. R. et al. Bridge resonance effects in singlet fission. J. Phys. Chem. A 124, 9392–9399 (2020).

    Article  CAS  PubMed  Google Scholar 

  31. Zirzlmeier, J. et al. Singlet fission in pentacene dimers. Proc. Natl Acad. Sci. USA 112, 5325–5330 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  32. Korovina, N. V., Pompetti, N. F. & Johnson, J. C. Lessons from intramolecular singlet fission with covalently bound chromophores. J. Chem. Phys. 152, 040904 (2020).

    Article  CAS  PubMed  Google Scholar 

  33. Davis, W. B., Svec, W. A., Ratner, M. A. & Wasielewski, M. R. Molecular-wire behaviour in p -phenylenevinylene oligomers. Nature 396, 60–63 (1998).

    Article  CAS  Google Scholar 

  34. Fuemmeler, E. G. et al. A direct mechanism of ultrafast intramolecular singlet fission in pentacene dimers. ACS Cent. Sci. 2, 316–324 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  35. Yablon, L. M. et al. Singlet fission and triplet pair recombination in bipentacenes with a twist. Mater. Horiz. 9, 462–470 (2022).

    Article  CAS  PubMed  Google Scholar 

  36. Quinn, J. R., Foss, F. W., Venkataraman, L., Hybertsen, M. S. & Breslow, R. Single-molecule junction conductance through diaminoacenes. J. Am. Chem. Soc. 129, 6714–6715 (2007).

    Article  CAS  PubMed  Google Scholar 

  37. Pariser, R. & Parr, R. G. A semi‐empirical theory of the electronic spectra and electronic structure of complex unsaturated molecules. I. J. Chem. Phys. 21, 466–471 (1953).

    Article  CAS  Google Scholar 

  38. Pople, J. A. Electron interaction in unsaturated hydrocarbons. Trans. Faraday Soc. 49, 1375 (1953).

    Article  CAS  Google Scholar 

  39. Smith, M. B. & Michl, J. Recent advances in singlet fission. Annu. Rev. Phys. Chem. 64, 361–386 (2013).

    Article  CAS  PubMed  Google Scholar 

  40. Berkelbach, T. C., Hybertsen, M. S. & Reichman, D. R. Microscopic theory of singlet exciton fission. II. Application to pentacene dimers and the role of superexchange. J. Chem. Phys. 138, 114103 (2013).

    Article  PubMed  Google Scholar 

  41. Khan, S. & Mazumdar, S. Diagrammatic exciton basis theory of the photophysics of pentacene dimers. J. Phys. Chem. Lett. 8, 4468–4478 (2017).

    Article  CAS  PubMed  Google Scholar 

  42. Khan, S. & Mazumdar, S. Theory of transient excited state absorptions in pentacene and derivatives: triplet–triplet biexciton versus free triplets. J. Phys. Chem. Lett. 8, 5943–5948 (2017).

    Article  CAS  PubMed  Google Scholar 

  43. Kittel, C. & Fong, C. Y. Quantum Theory of Solids (Wiley, 1987).

  44. Hele, T. J. H. et al. Anticipating acene-based chromophore spectra with molecular orbital arguments. J. Phys. Chem. A 123, 2527–2536 (2019).

    Article  CAS  PubMed  Google Scholar 

  45. Beljonne, D., Yamagata, H., Brédas, J. L., Spano, F. C. & Olivier, Y. Charge-transfer excitations steer the Davydov splitting and mediate singlet exciton fission in pentacene. Phys. Rev. Lett. 110, 226402 (2013).

    Article  CAS  PubMed  Google Scholar 

  46. Basel, B. S. et al. Evidence for charge-transfer mediation in the primary events of singlet fission in a weakly coupled pentacene dimer. Chem 4, 1092–1111 (2018).

    Article  CAS  Google Scholar 

  47. Busby, E. et al. A design strategy for intramolecular singlet fission mediated by charge-transfer states in donor–acceptor organic materials. Nat. Mater. 14, 426–433 (2015).

    Article  CAS  PubMed  Google Scholar 

  48. He, G. et al. Charge transfer states impact the triplet pair dynamics of singlet fission polymers. J. Chem. Phys. 153, 244902 (2020).

    Article  CAS  PubMed  Google Scholar 

  49. Monahan, N. & Zhu, X.-Y. Charge transfer-mediated singlet fission. Annu. Rev. Phys. Chem. 66, 601–618 (2015).

    Article  CAS  PubMed  Google Scholar 

  50. Tsuji, Y. & Yoshizawa, K. Frontier orbital perspective for quantum interference in alternant and nonalternant hydrocarbons. J. Phys. Chem. C 121, 9621–9626 (2017).

    Article  CAS  Google Scholar 

  51. Xia, J. et al. Breakdown of interference rules in azulene, a nonalternant hydrocarbon. Nano Lett. 14, 2941–2945 (2014).

    Article  CAS  PubMed  Google Scholar 

  52. Kumarasamy, E. et al. Tuning singlet fission in π-bridge-π chromophores. J. Am. Chem. Soc. 139, 12488–12494 (2017).

    Article  CAS  PubMed  Google Scholar 

  53. Aryanpour, K., Shukla, A. & Mazumdar, S. Theory of singlet fission in polyenes, acene crystals, and covalently linked acene dimers. J. Phys. Chem. C 119, 6966–6979 (2015).

    Article  Google Scholar 

  54. Ramasesha, S., Albert, I. D. L. & Sinha, B. Optical and magnetic properties of the exact PPP states of biphenyl. Mol. Phys. 72, 537–547 (1991).

    Article  CAS  Google Scholar 

  55. Khan, S. & Mazumdar, S. Optical probes of the quantum-entangled triple–triplet state in a heteroacene dimer. Phys. Rev. B 98, 165202 (2018).

    Article  CAS  Google Scholar 

  56. Chandross, M. & Mazumdar, S. Coulomb interactions and linear, nonlinear, and triplet absorption in poly(para-phenylenevinylene). Phys. Rev. B 55, 1497–1504 (1997).

    Article  CAS  Google Scholar 

  57. Tavan, P. & Schulten, K. Electronic excitations in finite and infinite polyenes. Phys. Rev. B 36, 4337–4358 (1987).

    Article  CAS  Google Scholar 

Download references

Acknowledgements

This work was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under award no. DE-SC0022036 (M.Y.S. and L.M.C.) and the National Science Foundation under award no. CHE-1764152 (S.M.). K.R.P. thanks the Department of Defense for a National Defense Science and Engineering (NDSEG) Fellowship. J.Z. thanks the Columbia College Science Scholars Program and Guthikonda Fellowship. X.Y. acknowledges the Beijing Institute of Technology Research Fund Program for Young Scholars, and the Analysis and Testing Center of Beijing Institute of Technology for NMR and mass spectrometry characterization. This research used resources at the Center for Functional Nanomaterials, which is a US DOE Office of Science Facility at Brookhaven National Laboratory under contract DE-SC0012704.

Author information

Authors and Affiliations

  1. Department of Chemistry, Columbia University, New York, NY, USA

    Kaia R. Parenti, Huaxi Huang, Daniel Malinowski, Jocelyn Zhang & Luis M. Campos

  2. Department of Physics, University of Arizona, Tucson, AZ, USA

    Rafi Chesler & Sumit Mazumdar

  3. Department of Physics, Graduate Center, City University of New York, New York, NY, USA

    Guiying He & Matthew Y. Sfeir

  4. Photonics Initiative, Advanced Science Research Center, City University of New York, New York, NY, USA

    Guiying He & Matthew Y. Sfeir

  5. Institute for Theoretical Solid State Physics, Leibniz IFW Dresden, Dresden, Germany

    Pritam Bhattacharyya

  6. Key Laboratory of Cluster Science, Ministry of Education of China, Beijing Key Laboratory of Photoelectronic/Electrophotonic Conversion Materials, School of Chemistry and Chemical Engineering, Beijing Institute of Technology, Beijing, P. R. China

    Beibei Xiao & Xiaodong Yin

  7. Department of Physics, Indian Institute of Technology Bombay, Mumbai, India

    Alok Shukla

  8. Department of Chemistry and Biochemistry, University of Arizona, Tucson, AZ, USA

    Sumit Mazumdar

Authors
  1. Kaia R. Parenti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rafi Chesler
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guiying He
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Pritam Bhattacharyya
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Beibei Xiao
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Huaxi Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Daniel Malinowski
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Jocelyn Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Xiaodong Yin
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Alok Shukla
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Sumit Mazumdar
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Matthew Y. Sfeir
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Luis M. Campos
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

S.M., M.Y.S and L.M.C. oversaw the project. K.R.P., M.Y.S. and L.M.C. designed the molecules. G.H. collected the transient absorption spectroscopy data and K.R.P., G.H. and M.Y.S. carried out data analysis. K.R.P., B.X., H.H., D.M. and J.Z. synthesized and characterized the molecules, supervised by X.Y. and L.M.C. The theory models were designed by S.M. and A.S. PPP calculations were carried out by R.C. and P.B. Density functional theory calculations were carried out by G.H. The paper was written by K.R.P., S.M., M.Y.S. and L.M.C. with contributions from all authors.

Corresponding authors

Correspondence to Sumit Mazumdar, Matthew Y. Sfeir or Luis M. Campos.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Peer review

Peer review information

Nature Chemistry thanks Ferdinand Grozema and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Density functional theory geometry calculations.

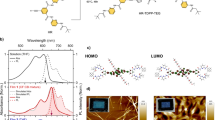
The ground state geometry of P–15N–P and P–16N–P are optimized using density functional theory (DFT) at the B3LYP/6-31G(d) level. Substitution at the 2, 6 and 7 positions of naphthalene gives a dihedral angle of ~35°, consistent with previous calculations on acene dimers10. Substitution at the 1 and 5 positions of naphthalene gives a more distorted structure with a dihedral angle of ~58°. As has been previously shown, singlet fission slows down considerably in highly twisted dimers10,11. We show the geometry of the twisted dimers and summarize all the naphthalene substitution positions and calculated dihedral angles in Extended Data Fig. 2.

Extended Data Fig. 2

Naphthalene substitution and corresponding dihedral angles calculated with DFT.

Source data

Extended Data Fig. 3 Hückel energy level distribution for T–N–T displaying the active space of 24 MOs.

The MRSDCI calculations are over an active space of MOs about the chemical potential that is smaller than the complete set. The lowest few bonding MOs are frozen (that is, excitations from these lowest MOs are not included in the CI calculations) and the highest MOs related to these by charge-conjugation symmetry are excluded from the active space. As of now, we have performed MRSDCI calculations over active spaces of 22–30 MOs, 11–15 bonding and 11–15 antibonding. These are absolutely the largest active spaces over which calculations of \(^1\left| {TT} \right\rangle\) have ever been done. We illustrate our procedure with the specific case of T–N–T. The localized tetracene Hückel bonding (red) and antibonding (blue) MOs, and the naphthalene (green) MOs constitute the active MO space in our T–N–T calculations. For calculations on T–Ph–T, T–A–T, P–Ph–P, P–N–P and P–A–P, we retained 20 + 4, 16 + 6, 20 + 4, 20 + 6 and 20 + 6 MOs, respectively, where the numbers in each sum indicate the chromophore MOs plus the linker MOs.

Extended Data Fig. 4 Time constants for singlet fission, triplet pair decay and free triplet decay.

Uncertainties are +/− 5%.

Source data

Supplementary information

Supplementary Information

Supplementary Figs. 1–12, discussion and Table 1.

Source data

Source Data Extended Data Fig. 2

Naphthalene substitution and corresponding dihedral angles calculated with DFT.

Source Data Extended Data Fig. 4

Time constants for singlet fission, triplet pair decay, and free triplet decay. Uncertainties are +/− 5%.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Parenti, K.R., Chesler, R., He, G. et al. Quantum interference effects elucidate triplet-pair formation dynamics in intramolecular singlet-fission molecules. Nat. Chem. 15, 339–346 (2023). https://doi.org/10.1038/s41557-022-01107-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41557-022-01107-8

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing