Abstract
The interaction between the supermassive black hole at the centre of the Milky Way, Sagittarius A*, and its accretion disk occasionally produces high-energy flares seen in X-ray, infrared and radio. One proposed mechanism that produces flares is the formation of compact, bright regions that appear within the accretion disk and close to the event horizon. Understanding these flares provides a window into accretion processes. Although sophisticated simulations predict the formation of these flares, their structure has yet to be recovered by observations. Here we show a three-dimensional reconstruction of an emission flare recovered from Atacama Large Millimeter/Submillimeter Array light curves observed on 11 April 2017. Our recovery shows compact, bright regions at a distance of roughly six times the event horizon. Moreover, it suggests a clockwise rotation in a low-inclination orbital plane, consistent with prior studies by GRAVITY and the Event Horizon Telescope. To recover this emission structure, we solve an ill-posed tomography problem by integrating a neural three-dimensional representation with a gravitational model for black holes. Although the recovery is subject to, and sometimes sensitive to, the model assumptions, under physically motivated choices, our results are stable and our approach is successful on simulated data.
Similar content being viewed by others
Main
The compact region around the Galactic Centre supermassive black hole Sagittarius (Sgr) A* is a unique environment where the magnetized turbulent flow of an accretion disk is subject to extreme gravitational physics. The dynamical evolution of this complex system occasionally leads to the production of energetic flares1 seen in X-ray2, infrared3 and radio4. The physical nature, structure, origin, formation and eventual dissipation of flares are topics of active research3,5,6,7,8 key to our understanding of accretion flows around black holes. One proposed explanation for Sgr A* flares is the formation of compact bright regions caused by hot pockets of lower-density plasma within the accretion disk, which are rapidly energized (for example, through magnetic reconnection9). These ‘bubbles’, ‘hotspots’ or ‘flux tubes’ observed in numerical simulations (for example, ref. 10) are hypothesized to form in orbit close to the innermost stable circular orbit (ISCO) of Sgr A*. The association of flares with orbiting hotspots close to the event horizon is consistent with near-infrared detections made by the GRAVITY Collaboration11,12 and radio observations of the Atacama Large Millimeter/Submillimeter Array (ALMA)13.
The context for this work is set by the first images14 of Sgr A* revealed by the Event Horizon Telescope (EHT) collaboration. The images, reconstructed from very-long-baseline interferometry observations from 6–7 April 2017, show a ring-like structure with a central brightness depression—a strong suggestion that the source is indeed a supermassive black hole15. Even in its quiescent state, imaged by EHT on 6–7 April, Sgr A* has shown considerable structural variability16. On 11 April 2017, Sgr A* was observed by ALMA directly after a high-energy flare seen in X-ray. The ALMA light curves exhibit an even higher degree of variability than 6–7 April4,17, including distinct coherent patterns in the linear polarization13 with variability on the scale of an orbit. The presence of synchrotron-radiating matter very close to the horizon of Sgr A* could potentially give rise to bright three-dimensional (3D) structures that orbit and evolve within the accretion disk. In this work, we present a 3D recovery of emission in orbit around Sgr A*, reconstructed from ALMA light curves observed on 11 April 2017 (Fig. 1).
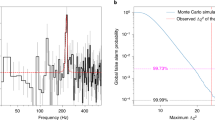
a, The validation-χ2, a robust data-fitting metric (Methods), indicates a preference of low inclination angles, θo < 18°, with a local minimum around θo = 12° (red curve). For each inclination, the 3D recovery is run with five random initializations, producing a spread that indicates recovery stability. The blue curve indicates that the analysis is largely insensitive to the black-hole spin. b, A recovered 3D volume visualized from two view angles in intrinsic (flat space) coordinates (the event horizon illustrated for size comparison). The recovery shows two emission regions (blue arrows) at radii of 11–13M (approximately six times the Schwarzschild radius).
To achieve this 3D reconstruction, we developed a new computational approach that we call orbital polarimetric tomography. In contrast to prior work by refs. 11,13, which employed a strongly constrained parametric hotspot model with only a handful of parameters to tune and interpret the observations, the goal of this work is to recover the complex 3D structure of flares as they orbit and evolve in the accretion disk around Sgr A*.
Tackling this inverse problem necessitates a change from typical tomography, wherein 3D recovery is enabled by multiple viewpoints. Instead, the tomography setting we propose relies on observing a structure in orbit, travelling through curved space-time, from a fixed viewpoint. As it orbits the black hole, the emission structure is observed (projected) along different curved ray paths. These observations of the evolving structure over time effectively replace the observations from multiple viewpoints required in traditional tomography. Our approach builds upon prior work on dynamical imaging and 3D tomography in curved space-time, which showed promising results in simulated future EHT observations18,19,20.
Similar to the computational images recovered by EHT16, our approach solves an underconstrained inverse problem to fit a model to the data. Nevertheless, ALMA observations do not resolve event horizon scales (~105 lower resolution), which makes the tomography problem we propose particularly challenging. To put it differently, we seek to recover an evolving 3D structure from a single-pixel observation over time. To solve this challenging task, we integrate the emerging approach of neural 3D representations20,21, which has an implicit regularization that favours smooth structures22 with physics constraints (details in Methods). The robustness of the results thus relies on the validity of the constraints imposed by the gravitational and synchrotron emission models.
We take advantage of the very high signal-to-noise and cadence of the ALMA dataset4, as well as the linear polarization information13. The choice to only fit the linear polarization (LP) light curves reflects the uncertainty associated with the unpolarized intensity of the background accretion disk. Although the total intensity light curve is dominated by the accretion disk, such extended emission structures are partially depolarized in an image-average sense13. In contrast, compact bright sources, such as a putative hotspot, are characterized by a large fractional LP and fast evolution on dynamical timescales13,23, hence allowing separation of the flare component from the background accretion. In Supplementary Information Section 2.2, we quantitatively assess the effect of the background accretion disk on simulated reconstruction results.
Results
On 11 April 2017, ALMA observed Sgr A* at ~230 GHz as part of a larger EHT campaign (Fig. 2, top). The radio observations directly followed a flare seen in the X-ray. The LP, measured by ALMA-only light curves4,13 as a complex time series Q(t) + iU(t), appears to evolve in a structured, periodic manner suggesting a compact emission structure in orbit. The work of ref. 13 hypothesizes a simple bright spot (that is, idealized point-source24 or spherical Gaussian25) at radius (r) ≈ 11M (where M is the black-hole mass; 2M is the Schwarzschild radius); however, a rigorous data fitting was not performed. Furthermore, the proposed parametric model is limited and does not explain all the data features. The orbital polarimetric tomography approach that we propose enables a rigorous data fitting and recovery of flexible 3D distributions of the emitting matter, relaxing the assumption of a fixed orbiting feature enforced by prior studies11,13,26. This opens a new window into understanding the spatial structure and location of flares relative to the event horizon.
Top: 229 GHz light curves were observed on 11 April 2017 (MJD 57854) as part of the EHT Sgr A* campaign. The red-shaded region corresponds to a time period of ~100 min in which polarimetric (Q–U) loops are apparent, directly after an X-ray flare was observed (grey-shaded region). The rotation of the polarization angle at a period similar to a Keplerian orbital period suggests the signal is coming from a bright compact structure in orbit around Sgr A*13. Bottom: a data fit is preformed on the intrinsic LP curves (centred and derotated). The model light curves are produced through ray tracing the estimated 3D volume at a fiducial inclination angle of θo = 12°. The resulting model light curves accurately describe the data, including the small looping feature highlighted by the blue arrow.
Our model, detailed in Methods, is able to fit the ALMA light curve data very accurately (Fig. 2, bottom). The optimization procedure simultaneously constrains the inclination angle of the observer and estimates a 3D distribution of the emitting matter associated with this flaring event, starting from 9:20 UT (~30 min after the peak of the X-ray flare13). Despite the fact that ALMA observations are unresolved (effectively a single pixel with time-dependent complex LP information) at the horizon scale, our analysis suggests some interesting insights:
-
Low inclination angles (θo < 18°, Fig. 1a, red) are preferred by the validation-χ2 (Methods). Although the methodology is different, this result is broadly consistent with EHT findings from 6–7 April27, which favoured low inclination angles of ~30° by comparing recovered images with general relativistic (GR) magnetohydrodynamic simulations. The fiducial model of ref. 13 corresponded to an inclination angle of ~22°. Low inclination was also favoured in the analysis of the GRAVITY infrared flares11,12,23.
-
The recovered 3D emission has two compact bright regions at r ≈ 11M and 13M (Fig. 1b). The location (radius and azimuthal position) of the bright region is consistent with the qualitative analysis of refs. 13,26.
Data fitting
Before solving the tomography problem, we perform preprocessing according to the procedure outlined in ref. 13. In particular, we time average the data, subtract a constant (time-averaged) LP component interpreted as the ring-like accretion disk component observed by the EHT and derotate the electric vector polarization angle to account for Faraday rotation (details in Methods). Figure 2 illustrates the data before and after the preprocessing.
To obtain a model prediction, a 3D emission structure is adjusted so that when placed in orbit, the numerically ray-traced light curves align with the observations. To recover the vertical structure, our approach primarily leverages asymmetries in the polarimetric radiative transfer. In particular, the geometry of space-time and the magnetic field dictate the angle of linear polarization (Q–U). Moving an emission point changes the observed angle of linear polarization. Thus, erroneously placing emission at time t = 0 and propagating it in time will rotate to the overall linear polarization in directions that are incompatible with the observed Q–U time series.
Computing the model predictions relies on ray tracing, which requires knowledge of the path rays take in 3D curved space-time. These geodesic paths depend on the unknown black-hole properties24: mass, spin and inclination. Nevertheless, the mass of Sgr A* is well constrained through stellar dynamics28; M ≃ 4 × 106 M⊙, where M⊙ denotes solar mass. Furthermore, Fig. 1 (blue curve) illustrates that the data fit is not very sensitive to black-hole spin: a ∈ [0, 1]. Thus, the only remaining unknown is the inclination angle.
To estimate the inclination, we numerically bin θo ∈ [0, π/2] and recover the 3D emission for every given (fixed) angle. For each angle, we recover a (locally) optimal 3D emission by minimizing a χ2 loss over the model parameters. Practically, for numerical stability, we avoid the extreme angles of face-on and edge-on by gridding θo ∈ [4°, 80°] (at 2° increments). Figure 1 plots the validation-χ2: a robust likelihood approximation for θo, which appears to favour low inclination angles (details in Methods). For each inclination, the recovery is run five times with a random initialization for the 3D structure. Therefore, the error bars are not a measure of posterior uncertainty; rather, they indicate the stability of the locally optimal solution.
An overview of the tomographic data-fitting framework is illustrated in Fig. 3. Mathematically, the 3D emission volume is estimated by minimizing a χ2 loss between the observed LP and the model prediction. The continuous 3D emission volume is represented by a coordinate-based, fully connected, neural network (‘neural representation’) and is constrained to a domain with a radius of 6M ≤ r ≤ 20M and close to the equatorial disk ∣z∣ ≤ 4M (6M is the ISCO of a non-spinning black hole). The data fit used in this work relies on the reduced χ2 definitions of ref. 29. This is not a strict definition of reduced χ2 that includes a normalization by the degrees of freedom. Rather, it is normalized by the total number of data points, which is useful for comparing fit quality in our experiments where degrees of freedom remain fixed.
(1) An orbital model propagates an initial (canonical) emission volume (e0) in time. (2) Ray tracing: we compute GR ray paths according to the black-hole parameters and numerically integrate the 3D emissivities to synthesize image-plane frames. (3) Each frame is summed to produce a single light curve data point that, downstream, is compared to the observations. (4) A neural representation of the underlying 3D volume. Each component is discussed extensively in Methods.
The ill-posed inverse problem we solve does not have a unique solution. The recovered 3D structure depends on, among other factors, the assumed inclination angle. Furthermore, solving a non-convex optimization problem with stochastic gradient descent methods leads to a local (and not global) minimum. Thus, the recovered 3D structure also depends on the random initialization of the network weights. Figure 4 highlights the robustness of the recovered 3D structure across different inclinations and initial conditions. Although this is not an exploration of the posterior distribution, the different recoveries give a sense of the solution’s stability. Qualitatively, the details of each recovered structure exhibit dependence on both the inclination angle and initialization. Nevertheless, some key features are consistent across these two axes. Although the exact angular extent of the structures is not stable, the azimuthal and radial positions appear stable and consistent with the average structure. Moreover, the separation of the emission into two distinct structures appears consistent across the different recoveries.
Although some of the details of the recovered structure depend on both axes, some key features remain consistent. The exact angular extent of the structures is not stable; nevertheless, the azimuthal and radial positions appear stable and consistent with the average structure highlighted in Fig. 1. Moreover, the separation into distinct emission regions of an elongated feature trailed by a smaller, dimmer, compact bright spot appears consistent across the different recoveries.
To analyse the ability to recover and detect different underlying 3D morphologies, we simulated synthetic datasets mimicking ALMA observations for three underlying 3D structures: simple hotspot, flux tube, double source. Figure 5 highlights the recovery results obtained from these datasets at two (unknown) inclination angles. A comprehensive analysis of the simulated datasets and reconstruction results is given in Supplementary Information Section 2.
Using synthetically generated light curves as observations, the 3D reconstructions are able to recover different flare morphologies in the presence of background accretion noise (not visualized in this figure). Further analysis and details are given in Supplementary Information Section 2.3.
Recovering the 3D structure from light curve observations is highly ill-posed. Thus, the recovery relies on physical constraints and model choices that we impose through the gravitational and synchrotron emission models. The robustness of the results depends on the validity of these model choices, detailed in Table 1 and discussed below.
The key assumption for orbital tomography is that the emission is in orbit within an accretion disk near the equatorial plane and can be modelled as a simple transformation to a canonical (or initial) 3D emission. Note that small shifts from the equatorial plane are allowed by our model. This enables the formulation of an inverse problem for estimating the 3D emission from observations. We consider orbits characterized by a Keplerian angular velocity profile (neglecting radial or vertical velocity components), accounting for shearing due to differential rotation (ignored by the previous analyses11,13,26) while neglecting the dynamics of cooling, heating, expansion and turbulence. Although this simplifying assumption does not hold in general, it is consistent with theoretical simulations10, which show consistent structures on short ~1 orbit timescales.
Furthermore, in modelling synchrotron emission, we assume a homogeneous vertical magnetic field that is externally fixed and is independent of the flare or accretion disk dynamics. The choice of a vertical magnetic field for the fiducial recovery is motivated by the notion that vertical magnetic fields could be powering Sgr A* flares, apparent in GR magnetohydrodynamic simulations that produce magnetic eruption events10. Moreover, from an observational standpoint, vertical magnetic fields are preferred by both the near-infrared analysis of GRAVITY11,12,23 and millimetre ALMA analysis of ref. 13. Nevertheless, the true spatial structure and dynamic properties of the magnetic fields around Sgr A* are largely unknown.
In Fig. 6, we analyse some of the systematic model choices detailed above by exploring the effects of (1) magnetic field configuration, (2) rotation direction and (3) sub-Keplerian orbits on the data fit and 3D reconstruction. It is important to note that we do not aim to exhaustively test all possible magnetic field and orbital velocity models, but instead highlight the sensitivity of our reconstruction to these model choices. The top-left panel of Fig. 6 compares the validation-χ2 for three magnetic field configurations: vertical, radial and toroidal, respectively, denoted by subscripts z, r and ϕ. For a radial magnetic field, the best-fit recovery is not a compact bright emission region (Fig. 6, bottom left). Rather, it is a fainter, diffuse structure. Even so, according to the data fit and consistent with prior studies, vertical magnetic fields are preferred with a lower validation-χ2 value.
Top: validation-χ2 under each model choice. Bottom: 3D reconstructions under various model assumptions. The red curve in all panels represents the fiducial model parameters: vertical magnetic field (Bz), CW rotation and Keplerian orbit (fK = 1.0). The global minimum for each curve is highlighted by a horizontal dashed line in the respective colour. Left: three different magnetic field configurations: vertical, radial and toroidal (subscripts z, r and ϕ, respectively). The recovered 3D under a radial magnetic field appears spread out rather than as a compact hotspot-like structure. That being said, consistent with the analysis of refs. 11,13, vertical magnetic fields, which do result in a compact hotspot-like structure, are favourable according to this metric, with lower validation-χ2 around θo = 12°. Centre: a comparison of CW and CCW angular velocity models. Consistent with the analysis of ref. 13, a CW rotation is preferred across all inclination angles. Right: a Keplerian orbit has the lowest validation-χ2 fit across three different fractions of sub-Keplerian orbit: fK = 1.0, 0.9 and 0.8. The recovery under fK = 0.9 (bottom right) is broadly consistent with the Keplerian model, with a tendency towards smaller radii (illustrated by the top-view panel).
The centre and rightmost panels in Fig. 6 highlight how clockwise rotation (CW) and a Keplerian orbit are favourable to anticlockwise rotation (CCW) or sub-Keplerian orbits, consistent with the analyses of GRAVITY23 and ref. 13. To test the fit of orbit direction and sub-Keplerian fraction, we set the angular velocity profile to Ω = ±fKΩK, where the ± sign dictates the direction (CW/CCW) and fK the magnitude (fK = 1 results in a clockwise Keplerian orbit). The 3D recovery under fK = 0.9 is shown in the bottom-right panel of Fig. 6, highlighting a broadly consistent recovery with the fiducial model assumptions. However, this consistency eventually breaks down at strong deviations from the Keplarian velocity assumption (also resulting in lower validation-χ2 values). The top view illustrates how a sub-Keplerian orbit impacts the recovered flare’s radial position.
Another key assumption made by our work is that the millimetre emission region is optically thin. This is consistent with both EHT observations of Sgr A* (ref. 17) and their theoretical interpretation16,27. Moreover, theoretical analysis10 has shown that a ‘flux tube’ flare would be optically thinner due to its higher temperature and lower density compared to the surrounding accretion flow.
Finally, we assume that the recovered emission structure is within the accretion disk. Although our model does not account for an alternative jet interpretation, the assumption of accretion flares is consistent with (1) theoretical simulations showing powerful equatorial current sheaths associated with flux eruptions forming within the accretion disk10, (2) observational evidence from EHT/very-long-baseline interferometry analyses consistent with a compact source model without any detectable jet contribution17,30,31 and (3) the GRAVITY detection, indicating an astrometric centre aligning with the mass centre, which implies that the orbiting feature is in proximity to the equatorial plane. The alternative scenario demands a precise alignment between the direction of the jet and the observer’s line of sight.
Discussion
We present a computational approach to image dynamic 3D structures orbiting the most massive objects in the universe. Integrating polarimetric general relativistic ray tracing and neural radiance fields enables resolving a highly ill-posed tomography in the extremely curved space-time induced by black holes. Applying this approach to ALMA observations of Sgr A* reveals a 3D structure of a flare, with a location broadly consistent with the qualitative analysis presented in ref. 13. This attempt at a 3D reconstruction of a Sgr A* flare suggests an azimuthally elongated bright structure at a distance of 11M trailed by a dimmer source at 13M. Although the recovered 3D is subject to and sometimes sensitive to the gravitational and emission models, under physically motivated choices, we find that the 3D reconstructions are stable and our approach is successful on simulated data. Moreover, our data-fit metrics provide constraints favouring low inclination angles and clockwise rotation of the orbital plane, supporting the analyses of ref. 13, EHT16 and GRAVITY11.
Orbital polarimetric tomography shows great promise for 3D reconstructions of the dynamic environment around a black hole. Excitingly, extending the approach and analysis to spatially resolved observations (for example, EHT) and multifrequency data could enable relaxing assumptions to further constrain the underlying physical structures that govern the black hole and plasma dynamics (for example, black-hole spin, orbit dynamics, magnetic fields). To that end, future work will likely need to extend our model to non-optically thin media and non-azimuthal velocity patterns. Lastly, by adapting orbital polarimetric tomography to other rich sources of black-hole time series observations (for example, quasars and microquasars), this imaging technology could open the door to population statistics and improve our understanding of black holes and their accretion processes.
Methods
In the following section, we describe our methodology, which is evaluated on synthetic simulations and analysed in the Supplementary Information.
Preprocessing
We reduced the ~100 min of ALMA light curves by time-averaging over ~1 min intervals, resulting in ~100 data points for each Stokes component. Following the procedures outlined in ref. 13, we subtract a constant LP component with magnitude and angle of Pdisk = 0.16 Jy and ξdisk = −37°, respectively, to account for the background accretion disk; we derotate the electric vector polarization angle by 32.2° to account for the estimated Faraday rotation13. We model the data as homoscedatic within a short and stable observation window with a polarimetric noise level estimated at σQ = σU = 0.01 Jy (ref. 13). Although we do not fit the total intensity, we regularize the model to have a total intensity around 0.3 Jy with a standard deviation of 0.15 Jy (ref. 13). Following ref. 13, we set 9:20 UT as the initial time of the analysis and 3D reconstruction of the flare. Supplementary Fig. 3 shows an analysis of different initial times around 9:20 UT, which provides further motivation for the selection of this initial time.
Forward model
In this section, we formulate the forward model, which takes a canonical 3D emission around a black hole as input and synthesizes light curves as output. Figure 3 provides a high-level overview of the forward model divided into four key building blocks, which we describe in the sections below.
Orbit dynamics
The key assumption for orbital tomography is that the four-dimensional emission e(t, x), where t denotes time and x denotes 3D spatial coordinates,is in orbit around the black hole and can be modelled as a simple transformation of a canonical (or initial) 3D emission, e0(x):
The transformation Tt propagates the initial 3D structure in time and connects dynamic observations, such as light curves, to the canonical 3D structure. This in turn enables formulating an inverse problem of estimating e0(x) from time-variable observations. Although the assumption of a coordinate transformation does not hold in general, it is well suited for compact, bright structures over short time scales, during which complex dynamics are negligible.
In our work, we consider a Keplerian orbit model with an angular velocity
where r is the distance from the black-hole centre and M is the black-hole mass. Note that for a = 0, equation (2) coincides with the Newtonian expression for angular velocity. A purely azimuthal orbit is suitable outside the ISCO, where radial velocities play a smaller role. Thus, we formulate the coordinate transformation as a shearing operation:
where Sϕ is a rotation matrix at an angle
The angular velocity dependence on r (equation (2)) causes shearing due to the faster motion of inner radii.
Image formation
In this section, we describe how e0 relates to light curve observations through an image-formation model. Each image pixel collects radiation along a geodesic curve: Γ(Θ, α, β) terminating at the image coordinates (α, β). The ray path Γ is determined by a handful of black-hole parameters: Θ = (M, a, θo). Omitting the explicit dependency on image coordinates (for brevity), we model image pixels through the polarized radiative transfer32,33,34 of an optically thin disk (attenuation can be neglected for Sgr A* 230 GHz observations27):
Equation (5) describes how pixel values are computed through an integration along geodesic curves Γ computed by solving a set of differential equations35 (Supplementary Information Section 3). The integrand comprises four elements: g, e, R and J. Here e(t + τx, x) is the unknown scalar emissivity that depends on microphysical properties (for example, local electron density and temperature) and τx is the time delay that accounts for photon travel time (often referred to as slow light). We model the polarized synchrotron radiation as this scalar emissivity function multiplied by a Stokes-vector J proportional to24
In this work, we consider only linear polarization, thus setting JV = 0. Moreover, the spectral index (reflecting the change in the local emission with frequency) is approximated as αν ≃ 1 (ref. 36). Note that the local emission frame is defined to align with Stokes Q; therefore, JU ≡ 0. The scaling factor qf ∈ [0, 1] is the (volumetric) fraction of linear polarization, and ϕB is the angle between the local magnetic field B and photon momentum k, given by
The two remaining quantities to define are R and g. The matrix R rotates the LP, (JQ, JU), from the emission frame to the image coordinates through parallel transport37 (Supplementary Information Section 3.4). The scalar field g(x) is a GR red-shift factor, which decreases the emission when the material is deep in the gravitational field or moving away from the observer. More generally, g(x) depends on the local direction of motion, u, relative to the photon momentum k:
Note that u and k are 4-vectors, more explicitly defined in Supplementary Information Section 3.
Light curves
For a given 3D emission, ray-tracing equation (5) enables computing a single pixel value over time. We compute light curves by numerically sampling a large field-of-view (FOV) and summing over image-plane coordinates:
Neural representation
We formulate a tomographic recovery relying on a neural representation20,21 of the unknown 3D volume: e0(x). Thus, instead of a traditional voxel discretization, the volume is represented by the weights, w, of a multilayer perceptron (MLP), that are adjusted to fit the observations.
The implicit regularization of the MLP architecture enables tackling highly ill-posed inverse problems20,38. The MLP takes continuously valued coordinates x as input and outputs the corresponding scalar emission at that coordinate
where γ(x) is a positional encoding of the input coordinates.
Studies have shown22 that encoding the coordinates instead of directly taking them as inputs can capture continuous fields better (converging in the width limit to a stationary interpolation kernel39). Thus, our work relies on a positional encoding that projects each coordinate onto a set of sinusoids with exponentially increasing frequencies:
The positional encoding controls the underlying interpolation kernel used by the MLP, where the parameter L determines the bandwidth of the interpolation kernel22.
In our work, we use a small MLP with four fully connected layers, where each layer is 128 units wide and uses ReLU activations. We use a maximum positional encoding degree of L = 3. The low degree of L is suitable for volumetric emission fields, which are naturally smooth20.
Once the neural network weights, w, are adjusted to fit the data, the network can be sampled at any 3D point, x, to produce the emission value at that point. This allows us to sample the network at regular grid points to extract a 3D volume representation of the recovered emission. Moreover, we can sample the network along straight-ray paths and ray trace the recovered emission as it would be seen by a perspective (pinhole) camera in flat space (used for the 3D visualizations throughout the Article).
Solving the inverse problem
In this section, we formulate an optimization approach that enables jointly estimating the 3D emission and inclination, which are the parameters of the forward model. Supplementary Fig. 1 shows a high-level illustration of the data-fitting procedure introduced in the following section.
Tomographic reconstruction
To estimate the 3D emission from light curve observations, we formulate a minimization problem. We estimate w, which parameterizes e0(x), by minimizing a χ2 data fit for each Stokes component, evaluated for a fixed set of black-hole parameters, Θ:
Here, we restrict the discussion to the total intensity and LP components: I, Q, U. Each χ2 is calculated as a sum over discrete temporal data points
where Nobs is the total number of data points; the subscript \(s=\left\{I,Q,U\,\right\}\) represents the stokes components; and ys, Is and σs are the polarimetric observations, model and noise standard deviation, respectively. Note that Is(ti, w∣Θ) is simply the light curve given by equation (11), sampled at discrete time ti, where w∣Θ highlight its dependency/conditioning on the network/black-hole parameters.
Equation (14) depends on unknown black-hole parameters; nevertheless, the mass of Sgr A* can be constrained through stellar dynamics28,40; M ≃ 4 × 106 M⊙, where M⊙ denotes solar masses. Furthermore, because the data fit is insensitive to black-hole spin, the only estimated parameter is the inclination angle. To estimate the inclination, we numerically bin θo ∈ [0, π/2] and recover the 3D emission by minimizing equation (14):
By interpreting equation (16) as a function of θo, we approximate the marginal log-likelihood as
Equation (17) is a zero-order expansion about the maximum likelihood estimator: w⋆.
Model selection using validation-χ 2
Although equation (17) tells us how well each model (inclination) fits the data, it is susceptible to overfitting. To mitigate overfitting, we define a more robust metric called validation-χ2 (Supplementary Fig. 5). The inclination angle is then estimated through the following procedure:
-
(1)
During optimization, ray positions are fixed to the centre of each image pixel. In our recoveries, we use an evenly sampled 64 × 64 grid for a FOV of 200 μarcsec.
-
(2)
We compute χ2 for perturbed pixel positions (off-centre) within a small pixel area. In our recoveries, we used a pixel area of 3.125 × 3.125 μarcsec2.
-
(3)
We average χ2 of 10 randomly sampled (uniform) ray positions to compute validation-χ2 curves.
-
(4)
\({\theta }_{{{{\rm{o}}}}}^{\star }\) is estimated as the global minimum of the validation-χ2.
Through simulations, we highlight how this procedure is a more robust selection criterion for models that are not overfitting the fixed ray positions (Supplementary Fig. 5).
Optimization procedure
The neural network was implemented in JAX41. Both the synthetic experiments (Supplementary Information Section 2) and the ALMA recovery were optimized using an ADAM optimizer42 with a polynomial learning rate transitioning from 1 × 10−4 → 1 × 10−6 over 50,000 iterations. Run times were ~1 h on two NVIDIA Titan RTX GPUs. Network weights were randomly initialized (Gaussian distributed) with several initial seeds.
Data availability
This paper makes use of the ALMA dataset ADS/JAO.ALMA#2016.1.01404.V, available through the ALMA data portal. Fully calibrated data and other materials are available from the corresponding author upon reasonable request.
Code availability
The software packages used to analyse the data are available at the following sites: kgeo (https://github.com/achael/kgeo) and bhnerf (https://github.com/aviadlevis/bhnerf).
References
Genzel, R. et al. Near-infrared flares from accreting gas around the supermassive black hole at the Galactic Centre. Nature 425, 934–937 (2003).
Neilsen, J. et al. A Chandra/HETGS census of X-ray variability from Sgr A* during 2012. Astrophys. J. 774, 42 (2013).
Fazio, G. G. et al. Multiwavelength light curves of two remarkable Sagittarius A* flares. Astrophys. J. 864, 58 (2018).
Wielgus, M. et al. Millimeter light curves of Sagittarius A* observed during the 2017 Event Horizon Telescope campaign. Astrophys. J. Lett. 930, L19 (2022).
Marrone, D. P. et al. An X-ray, infrared, and submillimeter flare of Sagittarius A*. Astrophys. J. 682, 373–383 (2008).
Haggard, D. et al. Chandra spectral and timing analysis of Sgr A*’s brightest X-Ray flares. Astrophys. J. 886, 96 (2019).
Dexter, J. et al. Sgr A* near-infrared flares from reconnection events in a magnetically arrested disc. Mon. Not. R. Astron. Soc. 497, 4999–5007 (2020).
Witzel, G. et al. Rapid variability of Sgr A* across the electromagnetic spectrum. Astrophys. J. 917, 73 (2021).
Broderick, A. E. & Loeb, A. Imaging bright-spots in the accretion flow near the black hole horizon of Sgr A*. Mon. Not. R. Astron. Soc. 363, 353–362 (2005).
Ripperda, B. et al. Black hole flares: ejection of accreted magnetic flux through 3D plasmoid-mediated reconnection. Astrophys. J. Lett. 924, L32 (2022).
GRAVITY Collaboration. Detection of orbital motions near the last stable circular orbit of the massive black hole SgrA*. Astron. Astrophys. 618, L10 (2018).
GRAVITY Collaboration. Modeling the orbital motion of Sgr A*’s near-infrared flares. Astron. Astrophys. 635, A143 (2020).
Wielgus, M. et al. Orbital motion near Sagittarius A*. Constraints from polarimetric ALMA observations. Astron. Astrophys. 665, L6 (2022).
Event Horizon Telescope Collaboration. First Sagittarius A* Event Horizon Telescope results. I. The shadow of the supermassive black hole in the center of the Milky Way. Astrophys. J. Lett. 930, L12 (2022).
Event Horizon Telescope Collaboration. First Sagittarius A* Event Horizon Telescope results. VI. Testing the black hole metric. Astrophys. J. Lett. 930, L17 (2022).
Event Horizon Telescope Collaboration. First Sagittarius A* Event Horizon Telescope results. III. Imaging of the Galactic Center supermassive black hole. Astrophys. J. Lett. 930, L14 (2022).
Event Horizon Telescope Collaboration. First Sagittarius A* Event Horizon Telescope results. II. EHT and multiwavelength observations, data processing, and calibration. Astrophys. J. Lett. 930, L13 (2022).
Tiede, P. et al. Spacetime tomography using the Event Horizon Telescope. Astrophys. J. 892, 132 (2020).
Levis, A., Lee, D., Tropp, J. A., Gammie, C. F. & Bouman, K. L. Inference of black hole fluid-dynamics from sparse interferometric measurements. In Proc. IEEE/CVF International Conference on Computer Vision (ICCV) 2021 (eds Berg, T. et al.) 2320–2329 (IEEE, 2021).
Levis, A., Srinivasan, P. P., Chael, A. A., Ng, R. & Bouman, K. L. Gravitationally lensed black hole emission tomography. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 2022 (eds Chellappa, R. et al.) 19809–19818 (IEEE, 2022).
Mildenhall, B. et al. NeRF: representing scenes as neural radiance fields for view synthesis. In Proc. European Conference on Computer Vision (ECCV) 2020 (eds Vedaldi, A. et al.) 405–421 (Springer, 2020).
Tancik, M. et al. Fourier features let networks learn high frequency functions in low dimensional domains. In Proc. Advances in Neural Information Processing Systems 33 (NeurIPS 2020) (eds Larochelle, H. et al.) 7537–7547 (NeurIPS, 2020).
Gravity Collaboration. Polarimetry and astrometry of NIR flares as event horizon scale dynamical probes for the mass of Sgr A*. Astron. Astrophys. 677, L10 (2023).
Gelles, Z., Himwich, E., Johnson, M. D. & Palumbo, D. C. M. Polarized image of equatorial emission in the Kerr geometry. Phys. Rev. D 104, 044060 (2021).
Vos, J., Mościbrodzka, M. A. & Wielgus, M. Polarimetric signatures of hot spots in black hole accretion flows. Astron. Astrophys. 668, A185 (2022).
Yfantis, A. I., Mościbrodzka, M. A., Wielgus, M., Vos, J. T. & Jimenez-Rosales, A. Fitting the light curves of Sagittarius A* with a hot spot model. Bayesian modeling of QU loops in the millimeter band. A&A https://doi.org/10.1051/0004-6361/202348230 (2023).
Event Horizon Telescope Collaboration. First Sagittarius A* Event Horizon Telescope results. V. Testing astrophysical models of the Galactic Center black hole. Astrophys. J. Lett. 930, L16 (2022).
Ghez, A. M. et al. Measuring distance and properties of the Milky Way’s central supermassive black hole with stellar orbits. Astrophys. J. 689, 1044 (2008).
Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope results. IV. Imaging the central supermassive black hole. Astrophys. J. Lett. 875, L4 (2019).
Issaoun, S. et al. The size, shape, and scattering of Sagittarius A* at 86 GHz: first VLBI with ALMA. Astrophys. J. 871, 30 (2019).
Cho, I. et al. The intrinsic structure of Sagittarius A* at 1.3 cm and 7 mm. Astrophys. J. Lett. 926, 108 (2022).
Chan, C. K., Psaltis, D. & Özel, F. GRay: a massively parallel GPU-based code for ray tracing in relativistic spacetimes. Astrophys. J. 777, 13 (2013).
Dexter, J. A public code for general relativistic, polarised radiative transfer around spinning black holes. Mon. Not. R. Astron. Soc. 462, 115–136 (2016).
Mościbrodzka, M. & Gammie, C. F. IPOLE—semi-analytic scheme for relativistic polarized radiative transport. Mon. Not. R. Astron. Soc. 475, 43–54 (2018).
Chael, A. kgeo (version 1.0.0). GitHub https://github.com/achael/kgeo (2023).
Narayan, R. et al. The polarized image of a synchrotron-emitting ring of gas orbiting a black hole. Astrophys. J. Lett. 912, 35 (2021).
Himwich, E., Johnson, M. D., Lupsasca, A. & Strominger, A. Universal polarimetric signatures of the black hole photon ring. Phys. Rev. D 101, 084020 (2020).
Zhong, E. D., Bepler, T., Berger, B. & Davis, J. H. CryoDRGN: reconstruction of heterogeneous cryo-EM structures using neural networks. Nat. Methods 18, 176–185 (2021).
Jacot, A., Gabriel, F. and Hongler, C. Neural tangent kernel: convergence and generalization in neural networks. In Proc. Advances in Neural Information Processing Systems 31 (NeurIPS 2020) (eds Bengio, S. et al.) 8571–8580 (2018).
Abuter, R. et al. Mass distribution in the galactic center based on interferometric astrometry of multiple stellar orbits. Astron. Astrophys. 657, L12 (2022).
Bradbury, J. et al. JAX: composable transformations of Python+NumPy programs. GitHub https://github.com/google/jax (2018).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Preprint at https://arxiv.org/abs/1412.6980 (2014).
Acknowledgements
We thank V. Ravi and B. Ripperda for fruitful discussions. This work was supported by National Science Foundation awards 1935980 and 2048237 and the Carver Mead New Adventures Fund. A.A.C. is supported by the Princeton Gravity Initiative. M.W.’s research is supported by the ERC advanced grant ‘M2FINDERS—Mapping Magnetic Fields with INterferometry Down to Event hoRizon Scales’ (grant no. 101018682).
Author information
Authors and Affiliations
Contributions
A.L. and K.L.B. identified and formulated the tomography problem and conceived and designed the experiments. A.L., K.L.B. and P.P.S. developed the neural representation-based tomography approach. A.A.C. and A.L. developed the polarimetric ray tracing. A.A.C formulated and implemented the geodesic computations. M.W. worked on data calibration. A.L. performed the tomographic reconstructions. All authors contributed to the analysis, interpretation, discussion and writing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Astronomy thanks the anonymous reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary analysis of simulations, Figs. 1–9 and details on general relativistic ray tracing.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Levis, A., Chael, A.A., Bouman, K.L. et al. Orbital polarimetric tomography of a flare near the Sagittarius A* supermassive black hole. Nat Astron 8, 765–773 (2024). https://doi.org/10.1038/s41550-024-02238-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41550-024-02238-3