Abstract
The immediate vicinity of an active supermassive black hole—with its event horizon, photon ring, accretion disk and relativistic jets—is an appropriate place to study physics under extreme conditions, particularly general relativity and magnetohydrodynamics. Observing the dynamics of such compact astrophysical objects provides insights into their inner workings, and the recent observations of M87* by the Event Horizon Telescope1,2,3,4,5,6 using very-long-baseline interferometry techniques allows us to investigate the dynamical processes of M87* on timescales of days. Compared with most radio interferometers, very-long-baseline interferometry networks typically have fewer antennas and low signal-to-noise ratios. Furthermore, the source is variable, prohibiting integration over time to improve signal-to-noise ratio. Here, we present an imaging algorithm7,8 that copes with the data scarcity and temporal evolution, while providing an uncertainty quantification. Our algorithm views the imaging task as a Bayesian inference problem of a time-varying brightness, exploits the correlation structure in time and reconstructs (2 + 1 + 1)-dimensional time-variable and spectrally resolved images. We apply this method to the Event Horizon Telescope observations of M87*9 and validate our approach on synthetic data. The time- and frequency-resolved reconstruction of M87* confirms variable structures on the emission ring and indicates extended and time-variable emission structures outside the ring itself.
Similar content being viewed by others
Main
To address the imaging challenge of time-resolved very-long-baseline interferometry (VLBI) data, we employ Bayesian inference. In particular, we adopt the formalism of information field theory (IFT)10 for the inference of field-like quantities such as the sky brightness. IFT combines the measurement data and any included prior information into a consistent sky brightness reconstruction and propagates the remaining uncertainties into all final science results. Assuming limited spatial, frequency and temporal variations, we can work with sparsely sampled data, such as the 2017 Event Horizon Telescope (EHT) observation of M87*.
A related method based on a Gaussian Markov model was proposed in ref. 11 and another approach based on constraining information distances between time frames was proposed in ref. 12. These methods impose fixed correlations in space or time, whereas our approach adapts flexibly to the demands of the data. We also enforce strict positivity of the brightness, and instead of maximizing the posterior probability we perform a variational approximation, taking uncertainty correlations between all model parameters into account.
Interferometers sparsely probe the Fourier components of the source brightness distribution. The measured Fourier modes, called visibilities, are determined by the orientation and distance of antenna pairs, while the Earth’s rotation helps to partly fill in the gaps by moving these projected baselines within the source plane. Since the source is time variable and we aim at a time-dependent reconstruction, the measurement data have to be subdivided into multiple separate image frames along the temporal axis, leading to an extremely sparse Fourier space coverage in every frame. In the case of the EHT observation of M87*, data were taken during four 8 h cycles spread throughout 7 d. All missing image information needs to be restored by the imaging algorithm, exploiting implicit and explicit assumptions about the source structure.
Physical sources, including M87*, evolve continuously in time. Images of these sources separated by time intervals that are short compared with the evolutionary timescale are thus expected to be strongly correlated. Imposing these expected correlations during the image reconstruction process can inform image degrees of freedom (DOFs) that are not directly constrained by the data.
In radio interferometric imaging, spatial correlations can be enforced by convolving the image with a kernel, either during imaging, as part of the regularization, or as a postprocessing step. In our algorithm, we use a kernel as part of a forward model, where an initially uncorrelated image is convolved with the kernel to generate a proposal for the logarithmic sky brightness distribution, which is later adjusted to fit the data. The specific structure of such a kernel can have substantial impact on the image reconstruction. We infer this kernel in a non-parametric fashion simultaneously with the image. This substantially reduces the risk of biasing the result by choosing an inappropriate kernel, at the cost of introducing redundancies between DOFs of the convolution kernel and those of the preconvolution image.
Metric Gaussian Variational Inference (MGVI) is a Bayesian inference algorithm that is capable of tracking uncertainty correlations between all involved DOFs, which is crucial for models with redundancies, while having memory requirements that grow only linearly with the number of DOFs13. It represents uncertainty correlation matrices implicitly without the need for an explicit storage of their entries, and provides uncertainty quantification of the final reconstruction in terms of samples drawn from an approximate Bayesian posterior distribution, with a moderate level of approximation. Compared with methods that provide a best-fit reconstruction, our approach provides a probability distribution, capturing uncertainty.
A limitation of the Gaussian approximation is its unimodality, as the posterior distribution is multimodal14. Representing multimodal posteriors in high dimensions is hard if not infeasible. Therefore, our results describe a typical mode of this distribution, taking the probability mass into account.
MGVI is the central inference engine of the Python package Numerical Information Field Theory (NIFTy)8,15,16, which we use to implement our imaging algorithm, as it permits the flexible implementation of hierarchical Bayesian models. NIFTy turns a forward model into the corresponding backward inference of the model parameters by means of automatic differentiation and MGVI. For time-resolved VLBI imaging, we therefore need to define a data model that encodes all relevant physical knowledge of the measurement process and the brightness distribution of the sky.
This forward model describes in one part the sky brightness, and in another part the measurement process. For the sky brightness, we require strictly positive structures with characteristic correlations in space, time and frequency. These brightness fluctuations can vary exponentially over linear distances and time intervals, which is represented by a log-normal prior with a Gaussian process kernel. The correlation structure of this process is assumed to be statistically homogeneous and isotropic for space, time and frequency individually and decoupled for each subdomain.
Consequently the correlations are represented by a direct outer product of rotationally symmetric convolution kernels, or equivalently by a product of one-dimensional, isotropic power spectra in the Fourier domain. We assume the power spectra to be close to power laws with deviations modelled as integrated Wiener processes on a double-logarithmic scale17. The DOFs, which finally determine the spatiotemporal correlation kernel, are inferred by MGVI alongside the sky brightness distribution. While the adopted model can only describe homogeneous and isotropic correlations, this symmetry is broken for the sky image itself by the data, which in general enforce heterogeneous and anisotropic structures.
The EHT Collaboration has published data averaged down to two frequency bands at 227 GHz and 229 GHz. Therefore, we employ a simplified model for the frequency axis: we reconstruct two separate, but correlated images for these bands, with a priori assumed log-normal deviation on the 1% level, which amounts to spectral indices of ±1 within 1 s.d. Our algorithm does not constrain the absolute flux of the two channels. Thus, we can recover the relative spectral index changes throughout the source but not the absolute ones. A detailed description of the sky model is outlined in Methods.
We further require an accurate model of the instrument response. Just as the prior model is informed by our physical knowledge of the source, the instrument model is informed by our knowledge of the instrument. We consider two sources of measurement noise that cause the observed visibilities to differ from the perfect sky visibilities, the first being additive Gaussian thermal noise, whose magnitude is provided by the EHT Collaboration in the dataset. The other component consists of multiplicative, systematic measurement errors, which are mainly caused by antenna-based effects, for example differences in the measurement equipment, atmospheric phase shift, and absorption of the incoming electromagnetic waves. This source of errors can be conveniently eliminated by basing the model on derived quantities (closure amplitudes and phases), which are not affected by it. All these effects can be summarized in one complex, possibly time-variable, number per telescope, containing the antenna gain factors and antenna phases.
For VLBI on a microarcsecond scale, these effects can be prohibitively large. Fortunately, certain combinations of visibilities are invariant under antenna-based systematic effects, so-called closure phases and closure amplitudes18. These quantities serve as the data for our reconstruction (for details refer to Methods).
We apply this method to the EHT data of the supermassive black hole M87*. With a shadow of the size of approximately four light days and reported superluminal proper motions of 6c (ref. 19), its immediate vicinity is expected to be highly dynamic and subject to change on a timescale of days. The exceptional angular resolution of the EHT allowed the EHT Collaboration to image the shadow of this supermassive black hole directly and to confirm its variability on a horizon scale.
In this Letter, we present a time- and frequency-resolved reconstruction of the shadow of M87* over the entire observational cycle of 7 d, utilizing correlation in all four dimensions (Fig. 1). The closure quantities do not contain information on the total flux or the absolute position of the source. Therefore, we normalize our results such that the flux in the entire ring is constant in time and agrees with the results from the EHT Collaboration for the first frame of our reconstruction. To achieve an alignment of the source even in the absence of absolute position information we start the inference with the data of only the first two observation days and continue with all data until convergence.
All figures are constrained to half the reconstructed field of view. The first row shows time frames of the image cube, one for each day. The second row visualizes the brightness for day N + 1 minus day N. Red and blue visualize increasing and decreasing brightness over time, respectively. The third row visualizes the relative difference in brightness over time. The overplotted contour lines show brightness in multiplicative steps of 1/√2 and start at the maximum of the posterior mean of our reconstruction. The solid lines correspond to factors of powers of two from the maximum.
Figure 2 displays the frequency-averaged sample mean image for the first observing day together with its pixel-wise uncertainty. In full agreement with the EHT result, our image shows an emission ring that is brighter on its southern part, most probably due to relativistic beaming effects. Additionally, we obtain two faint extended structures, positioned opposite each other along the southwestern and northeastern directions. They do not have the shape of typical VLBI-imaging artifacts, that is, they are not faint copies of the source itself, and similar structures do not appear in any of our validation examples. We conclude that these structures are either of physical origin or due to unmodelled effects of the measurement in our algorithm. These include baseline-based calibration artifacts such as polarization leakage3, and extended emission outside the field of view. The latter probably has only a small effect, as we do not use closures that contain intrasite baselines, and all others should be insensitive to the large-scale jet emission4. The detection of additional significant source features, compared with the results from the EHT Collaboration, is enabled by the usage of the data of all four observation days at once and thereby partially integration of the information.
The top row shows the reconstructed mean and relative error. Note that the small-scale structure in regions with high uncertainty in the error map is an artifact of the limited number of samples. The bottom left shows a saturated plot of the approximate posterior mean, revealing the emission zones outside the ring. The bottom right shows the result of the eht-imaging pipeline in comparison, saturated to the same scale and with overplotted contour lines. The overplotted contour lines show brightness in multiplicative steps of 1/√2 and start at the maximum of the posterior mean of our reconstruction. The solid lines correspond to factors of powers of two from the maximum.
Since our reconstruction is based on closure quantities that are not sensitive to absolute flux, the absolute spectral dependence is not constrained. Still, the relative spectral index variations with respect to an overall spectrum can be explored (top row of Supplementary Fig. 1). The map exhibits a higher relative spectral index in the southern portion of the ring, which coincides with its brightest emission spot. However, the uncertainty map indicates that this feature is not significant and similar features falsely appear in the validation (bottom row of Supplementary Fig. 1). Therefore, we do not report any significant structures in the spectral behaviour of M87* and continue our analysis with frequency-averaged time frames.
The sky brightness for each day of the observation together with the absolute and relative differences between adjacent days is displayed in Fig. 1. We report mild temporal brightness changes of up to 6% per day, in particular within the western and southern parts of the ring, validating the observations made in ref. 4. Figure 3 shows the detailed temporal evolution of a selected number of locations and areas. Our method consistently interpolates between observations. Supplementary Video 1 also demonstrates the continuous evolution. In several locations our reconstruction agrees with the EHT’s imaging results, whereas others clearly deviate. In particular, at location 7, which corresponds to the extended structure in the southwestern direction, the brightness decreases by about 5% between adjacent days throughout the entire observation. This hints at a real and non-trivial temporal evolution.
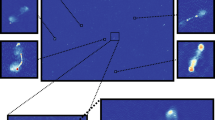
The brightness and flux for approximate posterior samples and their ensemble mean at specific sky locations and areas as indicated in the central panel. The peripheral panels show brightness and flux values of samples (thin lines) and their means (thick lines). Of these, the bottom right one displays the flux inside (red) and outside the circle (green), as well as the sum of the two (blue). For comparability, only brightness within the field of view of the EHT Collaboration image, indicated by the black box in the central plot, is integrated. The remaining panels give the local brightness for the different locations labelled by numbers in the central panel. The single-day results from EHT imaging are indicated as points with horizontal bars indicating the time interval over which the data were taken.
Following the analysis of ref. 4, we compute empirical characteristics of the asymmetric ring, that is, diameter d, width w, orientation angle η, azimuthal brightness asymmetry A and floor-to-ring contrast ratio fC. All findings are summarized in Table 1 and compared with the results of from EHT Collaboration4: We can confirm the stationary values for d, w, A and fC during the 7 d and a significant temporal evolution of η. The latter might be caused by flickering of emission spots20. We report a slightly larger d = (45 ± 3) μas, which does not significantly deviate from the result published by the EHT Collaboration of d = (42 ± 3) μas (ref. 1).
A collection of six validation examples has been assembled to assess the accuracy and robustness of our method (Fig. 4 and Supplementary Fig. 2). Supplementary Fig. 3 shows spatial correlation spectra for our scientific and validation images. Supplementary Fig. 4 displays the results of the imaging methods used by the EHT Collaboration together with our posterior mean and two samples for all observation periods. The temporal evolution of several samples is illustrated in Supplementary Video 2.
In the figure, time goes from left to right, showing slices through the image cube for the first time bin of each day. Different source models are shown from top to bottom: eht-crescent, slim-crescent and double-sources. For each source the ground truth, the approximate posterior mean of the reconstruction and the relative s.d., clipped to the interval [0, 1], are displayed (from top to bottom). The central three columns show moments in time for which no data are available since data were taken only during the first and last 2 d of the week-long observation period.
In conclusion, we present and validate a Bayesian imaging method that is capable of simultaneously reconstructing emission over spatial, temporal and spectral dimensions from closure quantities, utilizing correlation and quantifying uncertainties via posterior samples. We provide independent confirmation of the overall morphology of the emission ring around M87* and an apparent evolution of its orientation as published by the EHT Collaboration. The frequency resolution allows us to obtain a relative spectral index map, together with an uncertainty estimation. For the dataset at hand, significant spectral features could not be found. In addition to the emission ring, we resolve significant and potentially dynamic emission structures along the southwestern and northeastern directions. With future observations, our method may help to explore the intricate structure in the spatial, spectral and temporal domains of M87* and other variable sources. To achieve this, the model can be extended with inference of the prior spectral correlation structure.
Methods
The reconstruction algorithm relies on Bayesian statistics. Thus, it consists of three essential components: the likelihood, the prior and an inference scheme.
The likelihood is a probabilistic description of the measurement process including details of the measurement device. We choose to describe the measurement in terms of closure quantities that are invariant under antenna-based calibration effects.
The prior model captures all assumptions on the sky brightness distribution. Here we assume positivity at all times and correlation along the temporal, spatial and spectral directions, as well as the possibility of variations on an exponential scale. This is implemented with the help of a Gaussian process prior of the logarithmic brightness distribution with unknown kernel. Below, a non-parametric kernel model is derived that assumes a stochastic process along each dimension individually.
This constitutes a Bayesian inference problem that is approximately solved by applying MGVI as the inference scheme. This method requires a generative model formulation in which all model parameters are standard normal distributed a priori. The generative function defined below associates these with the physical quantities (Supplementary Fig. 5). We describe all implementation details and give the reasoning behind our choice of hyperparameters and the inference heuristic. The method is validated on six simulated sources with a varying degree of dynamics, ranging from simple shapes to realistic black holes. To demonstrate the effect of hyperparameter choices, we perform 100 reconstructions of both a synthetic example and M87* with randomized hyperparameters within a certain range. All validation efforts show that the algorithm is able to reconstruct synthetic examples successfully and is stable under changes in the hyperparameters.
Likelihood
The likelihood of the measured visibilities given the sky brightness distribution s is computed independently for each time frame. The visibilities for all measured data points are assumed to follow the measurement equation in the flat-sky approximation:
Here AB runs through all ordered pairs of antennas A and B for all non-flagged baselines, uAB and vAB are the coordinates of the measured Fourier points, s(x, y) is the sky brightness distribution as a function of sky angles x and y, and R is called the measurement response. The visibilities R(s)AB are complex numbers and we represent them in polar coordinates as phases \({\phi }_{\mathrm{AB}}(s)\in {\mathbb{R}}\) and logarithmic amplitudes \({\rho }_{\mathrm{AB}}(s)\in {\mathbb{R}}\), that is R(s)AB = exp[ρAB(s) + iϕAB(s)]. We assume the thermal noise of the phase and logarithmic amplitude to be independently Gaussian distributed with covariance
where dvis is the reported visibility data and σ is the reported thermal noise level. The operation diag(x) denotes a diagonal matrix with x on its diagonal. This is approximately valid for a signal-to-noise ratio larger than 5 (ref. 21), which is true for most of our data. To avoid antenna-based systematic effects, we compute closure quantities from these visibilities21. Closure phases are obtained by combining a triplet of complex phases of visibilities via
Closure amplitudes are formed by combining the logarithmic absolute value of four visibilities:
These closure quantities are invariant under antenna-based visibility transformations of the form
for all antennas and multiplicative calibration errors cA and cB, where * denotes the complex conjugate.
Note that forming the closure phases is a linear operation on the complex phase, while forming the closure amplitudes is linear in the logarithmic absolute value. We can thus represent these operations using matrices:
The closure matrices L and M are sparse and contain in every row ±1 for visibilities associated with the closure, and zero elsewhere.
The noise covariances Nρ and Nϕ of the closure quantities are related to N via
where † denotes the adjoint of the operator and \({{{\mathcal{N}}}}(n| 0,N)\) denotes a Gaussian distribution over n with mean 0 and covariance N. The mixing introduced by applying L and M leads to non-diagonal noise covariance matrices of the closure quantities.
For a given antenna set-up (of five or more antennas), more closure quantities can be constructed than visibilities are available, and therefore they provide a redundant description of the data. For the logarithmic amplitudes ρ, we first construct all possible closure quantities and then map to a non-redundant set using the eigendecomposition of Nρ. Specifically, we construct a unitary transformation Uρ where each column of the matrix is an eigenvector corresponding to a non-zero eigenvalue of Nρ. This transformation provides a map from the space of all possible closure amplitudes to the space of maximal non-redundant sets, with the additional property that the transformed noise covariance becomes diagonal. Specifically,
where Λρ denotes a diagonal matrix with the non-zero eigenvalues of Nρ on its diagonal. We can combine L and Uρ to form an operation that maps from the logarithmic amplitudes of visibilities ρ directly to the space of non-redundant closure amplitudes ϱ via
and use it to compute the observed, non-redundant closure amplitude ϱd from the published visibility data dvis = exp(ρd + iϕd).
The resulting likelihood for closure amplitudes reads
Closure phases are constructed differently to avoid problems induced by phase wraps. Adding or subtracting 2π to or from a phase does not change the result, and we need to preserve this symmetry in our algorithm. We can thus only add integer multiples of phases such as equation (4), and this prohibits using a direct matrix decomposition to find a maximal non-redundant closure set.
We build the closure sets to be used in the imaging with the help of a greedy algorithm that processes closure phases in the order of decreasing signal-to-noise ratio, as defined by the inverse of the diagonal of Nϕ (equation (8)). The algorithm collects closure sets into M until rank(M) = dim(ϕ), ensuring that ϕcl consists of a maximal non-redundant set. In principle, all maximal non-redundant closure sets are equivalent as long as we take the non-diagonal noise covariance into account. The concrete choice might have a minor impact for our approximation of the closure phase likelihood.
Within our closure set, we can decompose Nϕ into Uϕ and Λϕ. Instead of working with the phases ϕcl directly, we use their positions on the complex unit circle \({\mathrm{e}}^{{\mathrm{i}}{\phi }_{{{\text{cl}}}}}\) to define
This mitigates the problem of phase wraps at the price of approximating the corresponding covariance. This approximation yields errors below the 1% level if the signal-to-noise ratio is larger than 10. Most of the data points are above this threshold, and the error decreases quadratically with increasing signal-to-noise ratio. Since data with the lowest s.d. are also the most informative, we believe the impact of the approximation on the reconstruction to be negligible.
Given the closure phases on the unit circle φ, the corresponding phase likelihood can be written as
where \({\varphi }_{d}={U}_{\phi }\,{\mathrm{e}}^{{\mathrm{i}}M{\phi }_{d}}\). Note that equation (13) is a Gaussian distribution on complex numbers with the probability density function
and Hermitian covariance X. Complex and real Gaussian distributions differ only in their normalization constant. We do not distinguish between them explicitly, as the normalization is irrelevant for our variational approach.
Modelling the sky brightness
The sky brightness distribution sxtν is defined within a fixed field of view \({{{\varOmega }}}_{x}\subset {{\mathbb{R}}}^{2}\), a time interval \({{{\varOmega }}}_{t}=[0,\bar{t}]\) and frequency range \({{{\varOmega }}}_{\nu }\subset {\mathbb{R}}\), which renders it a field defined in space, time and frequency. We assume s to be a priori log-normal distributed:
The a priori correlation structure of the logarithmic sky brightness τ is encoded within the covariance T. Choosing a log-normal model allows the sky brightness to vary exponentially on linear spatial, temporal and frequency scales and ensures the positivity of the reconstructed intensity, similarly to refs. 22,23.
We perform a basis transformation to a standardized Gaussian distribution \({{{\mathcal{P}}}}({\xi }_{s})={{{\mathcal{N}}}}({\xi }_{s}| 0,{\mathbb{1}})\), which allows us to separate the correlation structure from its realization24. The new coordinates ξs have the same dimension as the original parameters, but are a priori independent:
This defines a generative model that turns standard normal distributed DOFs ξs into random variables s that are distributed according to equation (15). Although the information encoded in a distribution is invariant under coordinate transformations, MGVI depends on the choice of coordinates. Therefore, reformulating the entire inference problem in terms of standardized generative models is important to ensure that the prior information is fully captured by an approximation via MGVI. We visualize our generative model in Supplementary Fig. 5.
Correlations in space, time and frequency
We do not know the correlation structure of the logarithmic sky brightness a priori, so we include it as part of the model, which has to be inferred from the data. The different dimensions of the sky brightness are governed by completely distinct physical phenomena, which should be reflected in the model.
Setting up such correlations involves a number of intricate technicalities. The main idea is to model the correlations in space, time and frequency independently using the same underlying model and combine them via outer products. Doing this naively results in degenerate and highly unintuitive model parameters. The model we introduce in the following avoids these issues, but unfortunately requires a certain complexity.
For now we consider the correlation structure along the different subdomains individually. A priori we do not want to single out any specific location or direction for the logarithmic sky brightness, which corresponds to statistical homogeneity and isotropy. According to the Wiener–Khinchin theorem, such correlation structures T(i) with i ∈ {Ωx, Ωt, Ων} are diagonal in the Fourier domain and can be expressed in terms of a power spectrum \({p}_{{T}^{(i)}}(| k| )\):
where F(i) and k denote the Fourier transformation and Fourier coordinates associated with the space i, D(i) is the dimension of i, δ denotes the Kronecker delta and ∣k∣ is the Euclidean norm of k. We choose our Fourier convention such that no factors of 2π enter F(i), and thus its inverse has a factor of \(1/{(2\uppi )}^{{D}^{(i)}}\). As we build the model in terms of standardized coordinates ξs, we work with the square root of the correlation matrix
that converts these into τ = Aξs.
The amplitude spectrum p(i)(∣k∣) depends on the characteristic length scales of the underlying physical processes, which we do not know precisely. Our next task is to develop a flexible model for this spectrum that expresses our uncertainty and is compatible with a wide range of possible systems. We model the amplitude spectrum in terms of its logarithm:
We do not want to impose any functional basis for this logarithmic amplitude spectrum γ(i)(∣k∣), so we describe it non-parametrically using an integrated Wiener process in logarithmic l = log∣k∣ coordinates. This corresponds to a smooth (that is, differentiable) function, with exponential scale dependence25. In the logarithmic coordinates l, the zero mode ∣k∣ = 0 is infinitely far away from all other modes. Later on we deal with it separately and continue with all remaining modes for now.
The integrated Wiener process in logarithmic coordinates γi(l) reads
where l0 is the logarithm of the first mode greater than zero. Without loss of generality, we set the initial offset to zero. Later on we explicitly parameterize it in terms of a more intuitive quantity. The parameter m(i) is the slope of the amplitude on a double-logarithmic scale. It is a highly influential quantity, as it controls the overall smoothness of the logarithmic sky brightness distribution. Specifically, after exponentiation, the spectrum is given as a power law with multiplicative deviations, and the exponent of this power law is given by the slope. Therefore, a spectrum with slope zero indicates the absence of any spatial correlation in the image, whereas a slope of −1 indicates continuous and −2 differentiable brightness distributions along the respective axis26. The parameter η(i) describes how much the amplitude spectrum deviates from the power law. These deviations follow the smooth integrated Wiener process and can capture characteristic length scales of the logarithmic brightness distribution. Their precise shape is encoded in the realization \({\xi }_{\mathrm{W}}^{(i)} \sim {{{\mathcal{N}}}}({\xi }_{\mathrm{W}}^{(i)}| 0,{\mathbb{1}})\), which are also parameters of our model and follow a priori the standard Gaussian distribution. We do not want to fix the slope and deviations and therefore impose Gaussian and log-normal priors for j ∈ {m, η} respectively, with preference for a certain value \({\mu }_{j}^{(i)}\) and expected deviations \({\sigma }_{j}^{(i)}\) thereof:
The amplitude spectrum defines the expected variation \({\widetilde{U}}^{(i)}\) of the log brightness around its offset via
The relation between γ(i) and \({\widetilde{U}}^{(i)}\) is unintuitive, but it is critical to constrain the expected variation to reasonable values as it has a severe impact on a priori plausible brightness distributions. Therefore we replace the variance amplitude (that is, the square root of \({\widetilde{U}}^{(i)}\)) with a new parameter a(i):
Note that this step implicitly determines the offset of the Wiener processes in terms of a(i). We elevate a(i) to be a free model parameter and impose a log-normal model analogous to η(i) with hyperparameters \({\mu }_{a}^{(i)}\) and \({\sigma }_{a}^{(i)}\).
Next, we combine correlation structures in independent subdomains. For every one of these, in our case space, time and frequency, we use an instance of the model described above. We have not yet specified how to deal with the amplitude of the zero modes p(i)(0), and their treatment emerges from the combination of the subdomains. The overall correlation structure including all subdomains is given by the outer product of the subspaces:
This product introduces a degeneracy: α(A(i) ⊗ A(j)) = (αA(i)) ⊗ A(j) = A(i) ⊗ (αA(j)) for all \(\alpha \in {{\mathbb{R}}}^{+}\). With every additional subdomain we add one additional degenerate DOF. We can use this freedom to constrain the zero mode of the amplitude spectrum, and thus remove the degeneracy up to a global factor. For this we normalize the amplitudes in real space:
The zero mode of the normalized amplitude \({\widetilde{A}}^{(i)}\) can be fixed to the total volume V(i) of the space Ω(i). Consequently, the overall correlation structure is expressed as
The remaining multiplicative factor α globally sets the scale in all subdomains and has to be inferred from the data. Additionally, we put a log-normal prior with logarithmic mean μα and s.d. σα hyperparameters and a corresponding standard Gaussian parameter ξα on this quantity.
This was the last ingredient for the correlation structure along multiple independent subdomains and serves as a generative prior to infer the correlation structure in a space–time–frequency imaging problem. For the specific application to the EHT observations, however, only data averaged down to two narrow frequency channels are available. Therefore, as we do not expect to be able to infer a sensible frequency correlation structure using only two channels, we simplify equation (26) to explicitly parameterize the frequency correlations as
where ϵ is a hyperparameter that steers the a priori correlation between the frequency channels.
We briefly summarize all the required hyperparameters and how the generative model for the correlation structure is built. We start with the correlations in the individual subdomains, which we describe in terms of their amplitude spectra A(i)(ξ(i)). Four distinct standardized model parameters are inferred from the data, \({\xi }^{(i)}:=({\xi }_{m}^{(i)},{\xi }_{\eta }^{(i)},{\xi }_{\mathrm{W}}^{(i)},{\xi }_{a}^{(i)})\). The first describes the slope of the linear contribution to the integrated Wiener process. The second is related to the strength of the smooth deviations from this linear part. The third parameter describes the actual form of these deviations. Finally, the last one describes the real-space fluctuations of the associated field.
The hyperparameters are \({\mu }_{j}^{i}\) and \({\sigma }_{j}^{i}\) for j ∈ {m, η, a} specifying the expected mean and s.d. of m(i) and expected mean and s.d. for ln(η), ln(a), which are therefore enforced to be positive. In addition to these, we have to determine the global scale parameter α(ξα), for which we also specify μα and σα. We determine the values for the hyperparameters of the logarithmic quantities through an additional moment matching step by explicitly specifying the mean and s.d. of the log-normal distribution. The generative model for the correlation structure is therefore
Combining this with the generative model for the sky brightness itself we end up with the full model:
Our model is now standardized and all its parameters ξ = (ξA, ξs) follow a multivariate standard Gaussian distribution. The Bayesian inference problem is fully characterized by the negative logarithm (or information) of the joint probability distribution of data and parameters. Combining the closure likelihoods with the described sky brightness model therefore yields
where H0 is a constant that is independent of the latent variables ξ.
Metric Gaussian Variational Inference
So far, we have developed a probabilistic model in the generative form of the joint distribution of data and model parameters. In the end we want to know what the data tell us about the model parameters, as given in the posterior distribution according to Bayes’s theorem. Our model is non-conjugate and we cannot solve for the result analytically. Instead, we approximate the true posterior distribution with a Gaussian using variational inference.
This is fundamentally problematic, as we are approximating a multimodal posterior, which has multiple local optima, with a unimodal distribution. In the end, only one mode of the posterior will be captured by the variational distribution, underestimating the overall uncertainty. Some of these solutions can be considered equivalent. For example, the absolute source location is not constrained either by the closure phases or by the prior, but it is also irrelevant for the analysis. However, this shift invariance also introduces several unphysical and pathological modes in the posterior, which might have low probability mass, but are local optima. An example for this is the appearance of multiple or partial copies of the source all over the image.
Every reconstruction method that performs local optimization in the context of closure quantities potentially runs into these issues, and our approach is no exception. Our chosen method and several procedures in our inference heuristic partially mitigate these issues and provide robust results. While we do not observe these pathological features in our main results, they do occur in the hyperparameter validation (see below). One principled way to overcome them is posterior sampling, but the scale of the envisioned inference task with 7.4 × 106 parameters is prohibitively large.
We use MGVI, which allows us to capture posterior correlations between all model parameters, despite the large scale of the inference problem. MGVI is an iterative scheme that performs a number of subsequent Gaussian approximations \({{{\mathcal{N}}}}(\xi | \bar{\xi },{{\varXi }})\) to the posterior distribution. Instead of inferring a parameterized covariance, an expression based on the Fisher information metric evaluated at the intermediate mean approximations is used, that is, Ξ ≈ I(ξ)−1, with
The first two terms originate from the likelihood and the last from the prior. All of these are expressed in terms of computer routines and we do not have to store this matrix explicitly. This is a non-diagonal matrix capturing correlations between all parameters. To infer the mean parameter \(\bar{\xi }\) we minimize the Kullback–Leibler divergence between the true posterior and our approximation:
This quantity is an expectation value over the Gaussian approximation and measures the overlap between the true posterior and our approximation. As we minimize this quantity, the normalization of the posterior distribution is irrelevant and we can work with the joint distribution over data and model parameters, as given by equation (30). We estimate the KL divergence stochastically by replacing the expectation value through a set of samples from the approximation. The structure of the implicit covariance approximation allows us to draw independent samples from the Gaussian for a given location.
Using the mean of the Gaussian plus and minus samples corresponds to antithetic sampling27, which reduces the sampling variance considerably, leading to performance increases. MGVI now alternates between drawing samples for a given mean parameter and optimizing the mean given the set of samples. The main metaparameters of this procedure are the number of samples and how accurately the intermediate approximations are performed.
The procedure converges once the mean estimate \(\bar{\xi }\) is self-consistent with the approximate covariance. To minimize the KL divergence, we rely on an efficient quasi-second-order Newton–conjugate-gradient method in a natural gradient descent scheme. At the beginning of the procedure, the accuracy of KL and gradient estimates, as well as overall approximation fidelity, is not as important. In practice, we gradually increase the accuracy with the number of MGVI iterations to gain overall speedups.
Implementation details
We implement the generative model in NIFTy15, which also provides an implementation of MGVI utilizing autodifferentiation. We represent the spatial domain with 256 × 256 pixels, each with a length of 1 μas. In the time domain we choose a resolution of 6 h for the entire observation period of 7 d, thus obtaining 28 time frames. The implementation of the generative model utilizes the fast Fourier transform and thus defines the resulting signal on a periodic domain. To avoid artifacts in the time domain, we add another 28 frames to the end of the observed interval, resulting in a temporal domain twice this size.
For the frequency domain, only two channels are available, and we do not expect them to differ much from each other. Instead of inferring the correlation along this direction, as we do for the spatial and temporal axes, we assume a correlation between the two channels at the 99% level a priori, that is, we set ϵ = 0.01.
This adds another factor of 2 of required pixels to the reconstruction. For future reconstructions with deeper frequency sampling we can extend the model and treat this domain equivalently to the space and time domains. Overall we have to constrain 256 × 256 × 56 × 2 + power spectrum DOFs ≈ 7.4 × 106 pixel values with the data.
The Gaussian approximation to the closure likelihoods is only valid in high-signal-to-noise regimes21. We increase the signal-to-noise ratio by means of an averaging procedure, which subdivides each individual scan into equally sized bins with a length of approximately 2 min. To validate that this averaging is justified, we compare the empirical s.d. of averaged data values with the corresponding thermal noise s.d. and find their ratio to be 1.48 on average, consistent with the expected √2 for complex-valued data.
The intrasite baselines of ALMA–APEX and SMT–JCMT probe the sky at scales larger than our field of view. To avoid contamination from external sources, we flag these intrasite baselines and exclude closure quantities that involve the respective pair.
Hyperparameters
The hyperparameter choices for the presented reconstruction are given in Supplementary Table 1. All hyperparameters except ϵ come in pairs of mean μ and s.d. σ, parameterizing a Gaussian or log-normal distribution for a parameter. This indirect hyperparameter setting induces a form of parameter search on each parameter, restricting them to be within a few s.d. of the mean.
An exception to this is the frequency domain, for which we only have two channels available. Here, we set an a priori difference ϵ of 1%. This is of the same order of magnitude as the relative difference in frequency, which is 0.9%. The posterior can differ from this value, governed by the overall scale α. This parameter controls the a priori expected variance of the average logarithmic sky brightness mean and difference of the two frequencies. For this α, we set the mean 0.2 with s.d. 0.1. Since we normalize the flux of the final model, this parameter only controls the expected deviations of ϵ, and has no other major effect. A deviation of about half an e-fold would be expected with these hyperparameter settings, as it corresponds to the sum of two means.
Our choices regarding the remaining hyperparameter setting are motivated by being maximally agnostic with respect to the magnitude and shape of spatial correlations, while fixing the temporal correlations to be moderate. By constraining the a priori slope of the spatial amplitude to \({\mu }_{m}^{x}=-1.5\) with an s.d. of \({\sigma }_{m}^{(x)}=0.5\) we allow the model to express structures ranging from the rough Wiener process to the smooth integrated Wiener process within 1 s.d. The overall variance of the logarithmic sky brightness with respect to its spatial mean is set to be a priori log-normal distributed with mean 0.7 and s.d. 1. An s.d. larger than its mean induces a log-normal distribution with a heavy tail, thus allowing for potentially large posterior spatial fluctuations.
The flexibility parameter η specifies the degree to which the power spectrum can deviate from a power-law shape and thereby introduce characteristic length scales or timescales. We choose small values for its mean (0.01) and s.d. (0.001), discouraging such characteristic scales in both time and space. Still, strong deviations from a power law are possible if the data demand it (Supplementary Fig. 3). In the time domain we do not expect strong variability due to the physical scale of the system, extending over several light days. We express this through the slope of the temporal amplitude, setting its expected mean to \({\mu }_{m}^{(t)}=-4\) and s.d. \({\sigma }_{m}^{(t)}=0.5\), imposing long correlations in time. The overall fluctuations are again relatively unconstrained with mean 0.2 and s.d. 1.
To test the sensitivity of our method, we perform a dedicated hyperparameter study later.
Inference heuristic
Here we want to give the motivation behind the choices for our inference heuristic, as it is described in Supplementary Table 2. These are ad hoc, but using the described procedure provides robust results for all examples given the described set of hyperparameters.
Our initial parameterization corresponds to a signal configuration that is constant in time and shows a Gaussian shape centred in the field of view with s.d. of 30 μas. This breaks the translation symmetry of the posterior distribution, concentrating the flux towards the centre. It does not fully prevent the appearance of multiple source copies, but they are not scattered throughout the entire image. A similar trick is also employed in the eht-imaging pipeline.
The next issue we face is ‘source teleportation’. Close-by frames are well constrained by our assumed correlation, but the data gap of 4 d allows for solutions in which the source disappears at one place and reappears at another. This is also due to the lack of absolute position information and not prevented by our dynamics prior. To avoid these solutions, we start by initially only using data from the first 2 d. For these we recover one coherent source, which is extrapolated in time. Once we include the data of the remaining 2 d, the absolute location is already fixed and only deviations and additional information to previous times have to be recovered.
The appearance of multiple source copies can be attributed to multimodality of the posterior. The stochastic nature of MGVI helps, to some degree, to escape these modes towards more plausible solutions. Nevertheless, this is not enough for strongly separated optima. We therefore employ a tempering scheme during the inference. The phases constrain the relative locations in the image, whereas the amplitudes constrain the relative brightness. Smoothly aligning source copies while keeping the amplitudes constant is either impossible or numerically stiff. Allowing violation of the observed closure amplitudes for a short period of time makes it easier to align all copies to a single instance. We achieve this by not considering the closure amplitude likelihood during one intermediate step of MGVI. The same issue persists for the closure amplitudes. We therefore alternate between only phase likelihood and amplitude likelihood. In between these two we always perform a step using both likelihoods. We start this procedure after a fixed number of steps, allowing a rough source shape to form beforehand. In the end we use the full likelihood for several steps.
MGVI requires specification of the number of sample pairs used to approximate the KL divergence. The more samples we use, the more accurate the estimate, but the larger the overall computational load. We steadily increase the number of samples throughout the inference for two reasons. Initially the covariance estimate only inaccurately describes the posterior mode and a large number of samples would be a waste of computational resources. Additionally, fewer samples increase the stochasticity of the inference, which makes it more likely to escape pathological modes of the posterior. Towards the end, it is worth investing computational power into a large number of samples to obtain accurate uncertainty estimates.
Finally, we have to specify how and how well the KL is optimized in every MGVI step. At the beginning, we do not want to optimize too aggressively, as we only use a limited number of samples and we want to avoid an overfitting on the sample realizations. We therefore use the limited-memory BFGS28 method with an increasing number of steps. For the last period, where we have accurate KL estimates, we employ the more aggressive natural gradient descent equivalent to SciPy’s Newton-CG algorithm29 to achieve deep convergence.
To demonstrate the robustness of this procedure we perform the reconstruction of M87* and the six validation examples (see below) for five different random seeds: 35 full reconstructions in total. Using the described heuristic, we do not encounter any of the discussed pitfalls, and we obtain consistent results. This corresponds to a success rate of at least 97%.
Method validation on synthetic observations
We validate our method on six synthetic examples, three of which exhibit temporal variation. The first two time-variable examples are crescents with an evolution of the angular asymmetry on timescales similar to that measured by the EHT Collaboration for M87*. They are toy models of the vicinity of the black hole and are defined analogously to ref. 4 Section C.2:
where r0 is the ring radius, w the full-width at half-maximum of the ring and x, y, and t the space and time coordinates. We choose two sets of parameters. The first, called eht-crescent, follows the validation analysis of the EHT Collaboration4: r0 = 22 μas, A = 0.23 and w = 10 μas. The second, called slim-crescent, has a smaller radius, a more pronounced asymmetry and a sharper ring: r0 = 20 μas, A = 0.5 and w = 3 μas.
As a third example, called double-sources, we choose two Gaussian shapes b(t, x, y) with full-width at half-maximum r = 20 μas that approach each other,
where α is the time-dependent distance and ϕ the time-dependent angle:
The static examples consist of a uniform disk with blurred edges and two simulations of black holes, challenge1 and challenge2, taken from the EHT Imaging Challenge30. The brightness of the blurred disk with a diameter of 40 μas is given by
For our validation we simulate the M87* observation, using the identical UV coverage, frequencies and time sampling. We set the total flux of the example sources to 0.5 Jy and add the reported thermal noise from the original observation. We do not add non-closing errors, such as polarization leakage. We also ignore the existence of large-scale emission around the source, as it would be expected for M87*31. This kind of emission has a substantial contribution only to the intrasite baselines4. By excluding these, we make sure that the large-scale emission does not affect our results. The reconstruction follows the identical procedure as for M87*, using the same hyperparameters and pixel resolution.
The results of the dynamic examples versus the ground truth and the pixel-wise uncertainty are shown in Fig. 4. For all static examples, we do not find time variability in the reconstructions. Thus, we only show the first frame versus ground truth, smoothed ground truth and pixel-wise uncertainty in the figure. As the likelihood is invariant under shifts, offsets in the reconstruction are to be expected. We are able to recover the shapes of the different examples, irrespective of the source being static or not.
The ring-parameter analysis is applied to the two crescent scenarios as well. The results for the recovered d, w and η are shown in Supplementary Tables 3 and 4. Here we compare the ground truth with the analysis of the mean reconstruction, following the approach of the EHT Collaboration. To propagate the uncertainty estimate of our reconstruction directly, we can extract the crescent parameters of all samples individually to obtain a mean estimate with associated uncertainty. The variational approximation has the tendency to underestimate the true variance and in this case should be regarded more as a lower limit. For the estimation of the ring diameter we adopt the approach described in Appendix G of ref. 4 to correct the diameter for the bias due to finite resolution. We further discuss the recovered spatial correlation structures of the log brightness in Supplementary Section 1. Starting with the first crescent, we recover well d, η and A. The ground truth is within the uncertainty of both procedures. w of the crescent is below the angular resolution of the telescope, so it is not surprising that we do not fully resolve it in the reconstruction. Neither way to calculate the uncertainty accounts for the discrepancies. Interestingly, all quantities, except for the orientation angle, are static in time. For this example, we additionally show the temporal evolution of selected points in Supplementary Fig. 6, analogously to M87*. The reconstruction follows the dynamics of the ground truth, as indicated by the dashed line.
The reconstruction of slim-crescent proves more challenging. Due to the weak signal, we do not recover the faint part of the circle. For an accurate extraction of the ring parameters, however, this area is vital to constrain the radius. Here, we only recover the orientation angle well. The diameter estimate has large error bars when following the approach of the EHT Collaboration. In this scenario the uncertainty estimate appears too conservative. In contrast to this, using samples for the uncertainty provides smaller error bars. This could be due to the variational approximation, which tends to underestimate the true uncertainty.
The dynamics of the two Gaussian shapes are recovered accurately and our model correctly interpolates through the gap of 3 d without data.
Overall, our method is capable of accurately resolving dynamics that are comparable to those expected in M87*. Therefore, our findings regarding the temporal evolution of M87* may be trusted.
Supplementary Fig. 1 shows the relative spectral index of M87*, as well as the eht-crescent validation example. In both cases, an increased spectral index coincides with the brightest spot on the ring. This is not a feature of the validation example, as we use a constant spectral index throughout the source. The apparent feature could emerge from different coverage, as well as a bias due to the unimodal approximation. Nevertheless, these features are insignificant, as our reported posterior uncertainty is large enough to be consistent with a constant spectral index throughout the image. This finding is not surprising due to the small separation of the two channels. In principle our method is capable of providing a spectral index, but in this application the data are inconclusive.
The reconstructions of the three static examples are shown in Supplementary Fig. 2. For illustrative purposes we show not only the ground truth, but also a blurred image of the ground truth, which we obtain by convolving with a Gaussian beam of 12 μas. Overall, we recover the general shape and main features of the sources.
None of the validation reconstructions yield imaging artifacts that appear in any way similar to the elongated structure that our algorithm recovers in the southwestern and northeastern directions of M87*. In particular, the eht-crescent model is accurately recovered without a trace of spurious structures. We conclude that the elongated features of M87* are either of physical origin or due to baseline-based errors, and that they are not an artifact introduced by our imaging technique.
Hyperparameter validation
To study the sensitivity of our results with regard to hyperparameters, we repeat the reconstruction of M87*, as well as eht-crescent, with 100 randomized, but shared configurations. We do not vary the s.d.-related hyperparameters, but sample the corresponding mean hyperparameters uniformly within three respective s.d. For ϵ we sample logarithmically uniformly between 0.001 and 0.5. Some of these configurations are numerically unstable and will result in errors. Other configurations do not facilitate the emergence of a single source and exhibit typical VLBI artifacts, especially source doubling throughout the image. This behaviour is easy to detect and we label the results manually.
The resulting mean sky brightness distributions can be found in Supplementary Figs. 7 and 8. The algorithm fails in 30% of the cases, results in artifacts 5.5% of the time and facilitates the emergence of a single ring in 64.5% of all cases. All of the latter cases exhibit extended structures in the case of M87*, whereas we do not observe any similar features for eht-crescent. We are therefore confident that these do not originate from the choice of the hyperparameters.
For a considerable portion of the parameter configurations we do not find the shift of the brightness asymmetry. However, the results with a static source all exhibit a significantly higher reduced χ2 value compared with the reconstructions that feature a shift in brightness asymmetry. In 23% of all test cases we obtain reconstructions with shifting asymmetry, all of which are consistent with the main result of this paper. Supplementary Fig. 9 shows that all reported ring fit parameters of our main result, including their uncertainties, are fully consistent with the hyperparameter validation.
There are two possible explanations for the absence of asymmetry shifts. First, the prior on the temporal evolution already favours slow dynamics and sampling even more extreme values for this validation might lead to static reconstructions. Second, the inference heuristic was optimized for parameter sets similar to the one used for the main result and not for the large variety of cases. They numerically pose completely different challenges and might converge more slowly or exhibit different optima. Improvements in the heuristic would most probably lead to a more robust behaviour for a larger parameter range.
Method validation by verifying data consistency
The time-resolved residuals χ2 of the closure phases and amplitudes for all validation examples, as well as for M87*, are shown in Supplementary Table 5. Additionally, in Supplementary Fig. 10, we display the noise-weighted residuals for the M87* reconstruction for the four observation periods as a function of time. We show the residual values for all posterior samples and for both frequency channels. In Supplementary Fig. 11 we show residuals for three baselines on 11 April, similar to Fig. 13 of ref. 6. Note that the apparent time evolution is largely due to the rotation of the Earth, and not due to intrinsic source variability. Our inspection of the residuals validates that temporal changes in the data are captured by the reconstruction, as there is no systematic change of the residuals as time progresses for any of the four periods.
By using only closure quantities, station-dependent calibration terms have been fully projected out for our reconstruction. Since ref. 3 not only performs partial calibration but also estimates the magnitude of the residual gains, performing self-calibration on our reconstruction provides an important consistency check. Our reconstruction is not a single result but rather a collection of approximate posterior samples, so individual calibration solutions need to be computed for each of them. Thereby, we obtain an uncertainty estimate on the gains, which we expect to be consistent with the precalibrated gains from the telescope.
The negative log-amplitude gains for all stations and days are shown in Supplementary Fig. 12, and for reference Supplementary Fig. 13 depicts the sample-averaged dirty images of the calibrated data, overlaid with contours of the posterior mean image. We can reproduce the issues with the calibration of the station Large Millimeter Telescope that have been reported by the EHT Collaboration4. Apart from these, the precalibrated visibilities agree with our result within the uncertainty.
Data availability
The data on which this work is based have been published by the Event Horizon Collaboration3,4 and are available at ref. 9. We provide a set of 160 antithetic sample pairs of the sky brightness from the approximate posterior distribution, which can be used to propagate uncertainty to any derived quantity. The samples are available at ref. 32.
Code availability
The software sources used for producing the results of this publication are available at ref. 8.
References
Event Horizon Telescope Collaboration et al. First M87 Event Horizon Telescope results. I. The shadow of the supermassive black hole. Astrophys. J. Lett. 875, L1 (2019).
Event Horizon Telescope Collaboration et al. First M87 Event Horizon Telescope results. II. Array and instrumentation. Astrophys. J. Lett. 875, L2 (2019).
Event Horizon Telescope Collaboration et al. First M87 Event Horizon Telescope results. III. Data processing and calibration. Astrophys. J. Lett. 875, L3 (2019).
Event Horizon Telescope Collaboration et al. First M87 Event Horizon Telescope results. IV. Imaging the central supermassive black hole. Astrophys. J. Lett. 875, L4 (2019).
Event Horizon Telescope Collaboration et al. First M87 Event Horizon Telescope results. V. Physical origin of the asymmetric ring. Astrophys. J. Lett. 875, L5 (2019).
Event Horizon Telescope Collaboration et al. First M87 Event Horizon Telescope results. VI. The shadow and mass of the central black hole. Astrophys. J. Lett. 875, L6 (2019).
vlbi_resolve https://gitlab.mpcdf.mpg.de/ift/vlbi_resolve.
Arras, P. et al. Software for M87* reconstruction with information field theory. https://doi.org/10.5281/zenodo.5499896 (2021).
Event Horizon Telescope Collaboration. First M87 EHT results: calibrated data. CyVerse Data Commons https://doi.org/10.25739/g85n-f134 (2019).
Enßlin, T. A. Information theory for fields. Ann. Phys. (Berl.) 531, 1800127 (2018).
Bouman, K. L. et al. Reconstructing video of time-varying sources from radio interferometric measurements. IEEE Trans. Comput. Imaging 4, 512–527 (2018).
Johnson, M. D. et al. Dynamical imaging with interferometry. Astrophys. J. 850, 172 (2017).
Knollmüller, J. & Enßlin, T. A. Metric Gaussian Variational Inference. Preprint at https://arxiv.org/abs/1901.11033 (2019).
Sun, H. & Bouman, K. L. Deep probabilistic imaging: uncertainty quantification and multi-modal solution characterization for computational imaging. Preprint at https://arxiv.org/abs/2010.14462 (2020).
Arras, P. et al. NIFTy5: Numerical Information Field Theory v5. Astrophysics Source Code Library ascl:1903.008 (2019).
Goldman, M. On the first passage of the integrated Wiener process. Ann. Math. Stat. 42, 2150–2155 (1971).
Rogers, A. et al. The structure of radio sources 3c 273b and 3c 84 deduced from the ’closure’ phases and visibility amplitudes observed with three-element interferometers. Astrophys. J. 193, 293–301 (1974).
Biretta, J., Sparks, W. & Macchetto, F. Hubble Space Telescope observations of superluminal motion in the M87 jet. Astrophys. J. 520, 621–626 (1999).
Nalewajko, K., Sikora, M. & Różańska, A. Orientation of the crescent image of M87*. Astron. Astrophys. 634, A38 (2020).
Blackburn, L. et al. Closure statistics in interferometric data. Astrophys. J. 894, 31 (2020).
Chael, A. A. et al. High-resolution linear polarimetric imaging for the Event Horizon Telescope. Astrophys. J. 829, 11 (2016).
Chael, A. A. et al. Interferometric imaging directly with closure phases and closure amplitudes. Astrophys. J. 857, 23 (2018).
Kingma, D. P. & Welling, M. Auto-encoding variational Bayes. In 2nd International Conference on Learning Representations (ICLR, 2014).
Enßlin, T. A. & Frommert, M. Reconstruction of signals with unknown spectra in information field theory with parameter uncertainty. Phys. Rev. D 83, 105014 (2011).
Oksendal, B. Stochastic Differential Equations: an Introduction with Applications (Springer, 2013).
Kroese, D. P., Taimre, T. & Botev, Z. I. Handbook of Monte Carlo Methods Vol. 706 (Wiley, 2013).
Liu, D. C. & Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 45, 503–528 (1989).
Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272 (2020).
VLBI Imaging Challenge http://vlbiimaging.csail.mit.edu/imagingchallenge.
Kim, J.-Y. et al. The limb-brightened jet of M87 down to the 7 Schwarzschild radii scale. Astron. Astrophys. 616, A188 (2018).
Arras, P. et al. Time-resolved reconstruction of M87* (version 1.1). https://doi.org/10.5281/zenodo.4455340 (2021).
Acknowledgements
We thank L. Bester and I. Natarajan for discussions regarding VLBI imaging and the Schneefernerhaus for their hospitality and the five anonymous reviewers for numerous comments and in particular for providing the prototype of Supplementary Fig 5. P.A. acknowledges financial support by the German Federal Ministry of Education and Research (BMBF) under grant 05A17PB1 (Verbundprojekt D-MeerKAT). J.K. acknowledges financial support by the Excellence Cluster ORIGINS, which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC-2094-390783311.
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
All authors contributed text to this publication. P.A., P.F., P.H., J.K. and R.L. implemented and tested the instrument response, likelihood and model. J.K. developed the inference heuristic. P.A. and J.K. performed the hyperparameter study. P.F. and P.A. contributed the amplitude model which features outer products of power spectra. M.R. provided implementations and numerical optimization for many of the employed algorithms. T.E. coordinated the team and contributed to discussions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Astronomy thanks Oleg Smirnov, Matthew Lister and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Discussion, Figs. 1–13 and Tables 1–5.
Supplementary Video 1
Video of the mean M87* reconstruction over 7 d.
Supplementary Video 2
Video of the 16 M87* samples over 7 d.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arras, P., Frank, P., Haim, P. et al. Variable structures in M87* from space, time and frequency resolved interferometry. Nat Astron 6, 259–269 (2022). https://doi.org/10.1038/s41550-021-01548-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41550-021-01548-0