Abstract
X-ray reverberation echoes are assumed to be produced in the strongly distorted spacetime around accreting supermassive black holes. This signal allows us to spatially map the geometry of the inner accretion flow1,2—a region that cannot yet be spatially resolved by any telescope—and provides a direct measure of the black hole mass and spin. The reverberation timescale is set by the light travel path between the direct emission from a hot X-ray corona and the reprocessed emission from the inner edge of the accretion disk3,4,5,6. However, there is an inherent degeneracy in the reverberation signal between black hole mass, inner disk radius and height of the illuminating corona above the disk. Here we use a long X-ray observation of the highly variable active galaxy IRAS 13224−3809 to track the reverberation signal as the system evolves on timescales of a day7,8. With the inclusion of all the relativistic effects, modelling reveals that the height of the X-ray corona increases with increasing luminosity, providing a dynamic view of the inner accretion region. This simultaneous modelling allows us to break the inherent degeneracies and obtain an independent timing-based estimate for the mass and spin of the black hole. The uncertainty on black hole mass is comparable to the leading optical reverberation method9, making X-ray reverberation a powerful technique, particularly for sources with low optical variability10.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the plots in Fig. 2 and Extended Data Figs. 1 and 4 are included as source data in the Supplementary Information. All other data used in figures within this paper and other findings of this study are available from the corresponding author upon request. All data used in this work is publicly available. The XMM-Newton observations can be accessed from the XMM-Newton science archive (http://nxsa.esac.esa.int/nxsa-web/).
Code availability
All the code used for the data reduction is available from their respective websites. XSPEC is freely available online. The transfer function model KYNREVERB is available at https://projects.asu.cas.cz/stronggravity/kynreverb. The MCMC sampler EMCEE is available at http://emcee.readthedocs.io/en/stable/index.html, with the XSPEC implementation available at https://github.com/jeremysanders/xspec_emcee.
References
Reynolds, C. S., Young, A. J., Begelman, M. C. & Fabian, A. C. X-ray iron line reverberation from black hole accretion disks. Astrophys. J. 514, 164–179 (1999).
Uttley, P., Cackett, E. M., Fabian, A. C., Kara, E. & Wilkins, D. R. X-ray reverberation around accreting black holes. Astron. Astrophys. Rev. 22, 72–137 (2014).
Emmanoulopoulos, D., Papadakis, I. E., Dovciak, M. & McHardy, I. M. General relativistic modelling of the negative reverberation X-ray time delays in AGN. Mon. Not. R. Astron. Soc. 439, 3931–3950 (2014).
Chainakun, P., Young, A. J. & Kara, E. Relativistic X-ray reverberation modelling of the combined time-averaged and lag-energy spectra in AGN. Mon. Not. R. Astron. Soc. 460, 3076–3088 (2016).
Wilkins, D. R., Cackett, E. M., Fabian, A. C. & Reynolds, C. S. Towards modelling X-ray reverberation in AGN: piecing together the extended corona. Mon. Not. R. Astron. Soc. 458, 200–225 (2016).
Chainakun, P., Watcharangkool, A., Young, A. J. & Hancock, S. X-ray time lags in AGN: inverse-Compton scattering and spherical corona model. Mon. Not. R. Astron. Soc. 487, 667–680 (2019).
Alston, W. N. et al. The remarkable X-ray variability of IRAS 13224-3809—I. The variability process. Mon. Not. R. Astron. Soc. 482, 2088–2106 (2019).
Alston, W. N. Non-stationary variability in accreting compact objects. Mon. Not. R. Astron. Soc. 485, 260–265 (2019).
Peterson, B. M. et al. Central masses and broad-line region sizes of active galactic nuclei. II. A homogeneous analysis of a large reverberation-mapping database. Astrophys. J. 613, 682–699 (2004).
Buisson, D. J. K., Lohfink, A. M., Alston, W. N. & Fabian, A. C. Ultraviolet and X-ray variability of active galactic nuclei with Swift. Mon. Not. R. Astron. Soc. 464, 3194–3218 (2017).
Padovani, P. et al. Active galactic nuclei: what’s in a name? Astron. Astrophys. Rev. 25, 2 (2017).
Gallo, L. X-ray perspective of narrow-line Seyfert 1 galaxies. Proc. Sci. NLS1-2018, 034 (2018); https://pos.sissa.it/328/034/pdf
Parker, M. L. et al. The response of relativistic outflowing gas to the inner accretion disk of a black hole. Nature 543, 83–86 (2017).
Pinto, C. et al. Ultrafast outflows disappear in high-radiation fields. Mon. Not. R. Astron. Soc. 476, 1021–1035 (2018).
Jansen, F. et al. XMM-Newton Observatory—I. The spacecraft and operations. Astron. Astrophys. 365, L1–L6 (2001).
Chartas, G. et al. Measuring the innermost stable circular orbits of supermassive black holes. Astrophys. J. 837, 26–46 (2017).
Fabian, A. C. Broad iron lines in AGN and X-ray binaries. Astrophys. Space Sci. 300, 97–105 (2005).
Fabian, A. C. et al. Long XMM observation of the narrow-line Seyfert 1 galaxy IRAS 13224-3809: rapid variability, high spin and a soft lag. Mon. Not. R. Astron. Soc. 429, 2917–2923 (2013).
Jiang, J. et al. The 1.5 Ms observing campaign on IRAS 13224-3809—I. X-ray spectral analysis. Mon. Not. R. Astron. Soc. 477, 3711–3726 (2018).
Fabian, A. C. et al. Broad line emission from iron K- and L-shell transitions in the active galaxy 1H0707-495. Nature 459, 540–542 (2009).
Kara, E. et al. A global look at X-ray time lags in Seyfert galaxies. Mon. Not. R. Astron. Soc. 462, 511–531 (2016).
Ingram, A. et al. A public relativistic transfer function model for X-ray reverberation mapping of accreting black holes. Mon. Not. R. Astron. Soc. 488, 324–347 (2019).
Kara, E., Fabian, A. C., Cackett, E. M., Miniutti, G. & Uttley, P. Revealing the X-ray source in IRAS 13224-3809 through flux-dependent reverberation lags. Mon. Not. R. Astron. Soc. 430, 1408–1413 (2013).
Dovciak, M. et al. Reverberation mapping in the lamp-post geometry of the compact corona illuminating a black-hole accretion disc in AGN. Preprint at http://www.cosmos.esa.int/web/xmm-newton/2014-symposium/ (2014).
Miniutti, G. & Fabian, A. C. A light bending model for the X-ray temporal and spectral properties of accreting black holes. Mon. Not. R. Astron. Soc. 349, 1435–1448 (2004).
McHardy, I. M., Koerding, E., Knigge, C., Uttley, P. & Fender, R. P. Active galactic nuclei as scaled-up galactic black holes. Nature 444, 730–732 (2006).
Taylor, C. & Reynolds, C. S. X-ray reverberation from black hole accretion disks with realistic geometric thickness. Astrophys. J. 868, 109–125 (2018).
Haardt, F. & Maraschi, L. A two-phase model for the X-ray emission from Seyfert galaxies. Astrophys. J. 380, L51–L54 (1991).
Wilkins, D. R. & Gallo, L. C. Driving extreme variability: the evolving corona and evidence for jet launching in Markarian 335. Mon. Not. R. Astron. Soc. 449, 129–146 (2015).
Kara, E. et al. The corona contracts in a black-hole transient. Nature 565, 198–201 (2019).
Struder, L., Briel, U., Dennerl, K. & Hartmann, R. The European photon imaging camera on XMM-newton: the pn-CCD camera. Astron. Astrophys. 365, L18–L26 (2001).
Bendat, J. & Piersol, A. Random Data: Analysis and Measurement Procedures (Wiley, 1986).
Vaughan, B. A. & Nowak, M. A. X-ray variability coherence: how to compute it, what it means, and how it constrains models of GX 339-4 and Cygnus X-1. Astrophys. J. 474, L43–L46 (1997).
Epitropakis, A. et al. Theoretical modelling of the AGN iron line vs. continuum time-lags in the lamp-post geometry. Astron. Astrophys. 594, A71 (2016).
Epitropakis, A. & Papadakis, I. E. The X-ray continuum time-lags and intrinsic coherence in AGN. Mon. Not. R. Astron. Soc. 468, 3568–3601 (2017).
Caballero-Garcıa, M. D. et al. Testing the X-ray reverberation model KYNREFREV in a sample of Seyfert 1 active galactic nuclei. Mon. Not. R. Astron. Soc. 480, 2650–2659 (2018).
Ross, R. R. & Fabian, A. C. A comprehensive range of X-ray ionized-reflection models. Mon. Not. R. Astron. Soc. 358, 211–216 (2005).
Arevalo, P. & Uttley, P. Investigating a fluctuating-accretion model for the spectral-timing properties of accreting black hole systems. Mon. Not. R. Astron. Soc. 367, 801–814 (2006).
Zoghbi, A., Uttley, P. & Fabian, A. C. Understanding reverberation lags in 1H0707-495. Mon. Not. R. Astron. Soc. 412, 59–64 (2011).
Alston, W. N., Vaughan, S. & Uttley, P. The flux-dependent X-ray time lags in NGC 4051. Mon. Not. R. Astron. Soc. 435, 1511–1519 (2013).
Alston, W. N., Done, C. & Vaughan, S. X-ray time delays in the narrow line Seyfert 1 galaxy PG 1244+026. Mon. Not. R. Astron. Soc. 439, 1548–1555 (2014).
Foreman-Mackey, D., Hogg, D. W., Lang, D. & Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 125, 306–312 (2013).
Gelman, A., Carlin, J., Stern, H. & Rubin, D. Bayesian Data Analysis 2nd edn (Taylor & Francis, 2003).
Vaughan, S., Edelson, R., Warwick, R. S. & Uttley, P. On characterizing the variability properties of X-ray light curves from active galaxies. Mon. Not. R. Astron. Soc. 345, 1271–1284 (2003).
Alston, W. N. et al. Discovery of an ~2-h high-frequency X-ray QPO and iron Kα reverberation in the active galaxy MS 2254.9-3712. Mon. Not. R. Astron. Soc. 449, 467–476 (2015).
Parker, M. L. et al. Revealing the X-ray variability of AGN with principal component analysis. Mon. Not. R. Astron. Soc. 447, 72–96 (2015).
Parker, M. L. et al. Revealing the ultrafast outflow in IRAS 13224-3809 through spectral variability. Mon. Not. R. Astron. Soc. 469, 1553–1558 (2017).
Mizumoto, M. et al. Can the relativistic light bending model explain X-ray spectral variations of Seyfert galaxies? Publ. Astron. Soc. Jpn 70, 42 (2018).
Yamasaki, H., Mizumoto, M., Ebisawa, K. & Sameshima, H. Origin of the characteristic X-ray spectral variations of IRAS 13224-3809. Publ. Astron. Soc. Jpn 68, 80 (2016).
Mizumoto, M. et al. X-ray short-time lags in the Fe-K energy band produced by scattering clouds in active galactic nuclei. Mon. Not. R. Astron. Soc. 478, 971–982 (2018).
Mizumoto, M. et al. X-ray reverberation lags of the Fe–K line due to AGN disc winds. Mon. Not. R. Astron. Soc. 482, 5316–5326 (2019).
Uttley, P. & McHardy, I. M. The flux-dependent amplitude of broadband noise variability in X-ray binaries and active galaxies. Mon. Not. R. Astron. Soc. 323, L26–L30 (2001).
Uttley, P., McHardy, I. M. & Vaughan, S. Non-linear X-ray variability in X-ray binaries and active galaxies. Mon. Not. R. Astron. Soc. 359, 345–362 (2005).
Vaughan, S. & Uttley, P. Studying accreting black holes and neutron stars with time series: beyond the power spectrum. Proc. SPIE 6603, Noise and Fluctuations in Photonics, Quantum Optics, and Communications 660314 (2007); https://doi.org/10.1117/12.724650
Gleissner, T. et al. Long term variability of Cyg X-1. II. The rms–flux relation. Astron. Astrophys. 414, 1091–1104 (2004).
Heil, L. M. & Vaughan, S. The linear rms–flux relation in an ultraluminous X-ray source. Mon. Not. R. Astron. Soc. 405, L86–L89 (2010).
Scaringi, S. et al. The universal nature of accretion-induced variability: the rms–flux relation in an accreting white dwarf. Mon. Not. R. Astron. Soc. 421, 2854–2860 (2012).
Heil, L. M., Vaughan, S. & Uttley, P. The ubiquity of the rms–flux relation in black hole X-ray binaries. Mon. Not. R. Astron. Soc. 422, 2620–2631 (2012).
Scaringi, S. A physical model for the flickering variability in cataclysmic variables. Mon. Not. R. Astron. Soc. 438, 1233–1241 (2014).
Vaughan, S., Uttley, P., Pounds, K. A., Nandra, K. & Strohmayer, T. E. The rapid X-ray variability of NGC 4051. Mon. Not. R. Astron. Soc. 413, 2489–2499 (2011).
Dobrotka, A. & Ness, J.-U. Differences in the fast optical variability of the dwarf nova V1504 Cyg between quiescence and outbursts detected in Kepler data and simulations of the rms–flux relations. Mon. Not. R. Astron. Soc. 451, 2851–2862 (2015).
Scaringi, S. et al. Accretion-induced variability links young stellar objects, white dwarfs, and black holes. Sci. Adv. 1, e1500686 (2015).
Van de Sande, M., Scaringi, S. & Knigge, C. The rms–flux relation in accreting white dwarfs: another nova-like variable and the first dwarf nova. Mon. Not. R. Astron. Soc. 448, 2430–2437 (2015).
Cowperthwaite, P. S. & Reynolds, C. S. Nonlinear dynamics of accretion disks with stochastic viscosity. Astrophys. J. 791, 126–134 (2014).
Hogg, J. D. & Reynolds, C. S. Testing the propagating fluctuations model with a long, global accretion disk simulation. Astrophys. J. 826, 40–59 (2016).
Lyubarskii, Y. E. Flicker noise in accretion discs. Mon. Not. R. Astron. Soc. 292, 679–685 (1997).
Kotov, O., Churazov, E. & Gilfanov, M. On the X-ray time-lags in the black hole candidates. Mon. Not. R. Astron. Soc. 327, 799–807 (2001).
King, A. R., Pringle, J. E., West, R. G. & Livio, M. Variability in black hole accretion discs. Mon. Not. R. Astron. Soc. 348, 111–122 (2004).
Ingram, A. & van der Klis, M. An exact analytic treatment of propagating mass accretion rate fluctuations in X-ray binaries. Mon. Not. R. Astron. Soc. 434, 1476–1485 (2013).
Risalitti et al. A rapidly spinning supermassive black hole at the centre of NGC 1365. Nature 494, 449–451 (2013).
Acknowledgements
W.N.A. and A.C.F. acknowledge support from the European Research Council through Advanced Grant 340442, on Feedback. M.L.P. and C.P. acknowledge support from ESA Research Fellowships. M.D. and M.D.C.-G. acknowledge support provided by the GA CR grant 18-00533S. M.D.C.-G. acknowledges funding from ESA through a partnership with IAA-CSIC (Spain). D.J.W. and M.J.M. appreciate support from an Ernest Rutherford STFC fellowship. D.J.K.B. acknowledges a Science and Technology Facilities Council studentship. C.S.R. thanks the UK Science and Technology Facilities Council for support under Consolidated Grant ST/R000867/1. This research has been partially funded by the Spanish State Research Agency (AEI) project no. ESP2017-87676-C5-1-R and no. MDM-2017-0737 Unidad de Excelencia “María de Maeztu”—Centro de Astrobiología (CSIC-INTA). G.M. acknowledges funding by the Spanish State Research. Agency (AEI) project no. ESP2017-86582-C4-1-R. B.D.M. acknowledges support from the European Union’s Horizon 2020 research and innovation programme under the Marie Skodowska-Curie grant agreement no. 798726. This paper is based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA member states and the United States (NASA).
Author information
Authors and Affiliations
Contributions
W.N.A. performed the data analysis and lag modelling, and wrote the manuscript. E.K. performed a complementary time-lag data analysis. C.P. and J.J. performed the time-averaged spectral modelling. M.L.P. performed the rms-spectrum modelling. The remaining authors contributed to the discussion and interpretation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
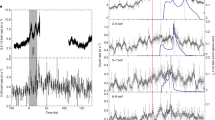
Extended Data Fig. 1 Lag frequency spectra for the 16 XMM-Newton orbits.
The best-fitting transfer function model, where MBH, spin a, Rin and inclination i are tied, but free, is shown in black solid line. The reverberation component is shown in red and the intrinsic component is shown in dotted grey. The zero time-lag as a function of frequency is shown as a black horizontal line. The black circles are the data with their 1σ error bars. The time-lag estimate at 2x10-4 Hz in observation 3039 has τ = 307 ± 87 s, but is clipped from the plotting region. The lower panels show the standard residuals.
Extended Data Fig. 2 Table of source properties and best-fitting model posteriors.
Column 1 shows the XMM-Newton orbit number. Column 2 shows the 2–10 keV luminosity in units of 1042 ergs-1. Column 3 shows the photon index Γ from the time-averaged spectral model fits. Column 4 shows the posterior values for source height h from best-fitting the transfer function model fit with parameters Rin, inclination i and spin free and tied across the lag spectra.
Extended Data Fig. 3 Posterior distributions for source height from the best fitting model.
The model has parameters MBH, Rin, inclination i and spin a, free and tied. The median and 68% credible regions (equivalent to 1σ of a Gaussian distribution) are shown in grey.
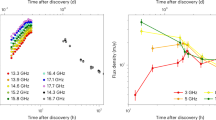
Extended Data Fig. 4 L2–10 keV luminosity vs source height h from the model fit with fixed spin.
Panel a shows the spin value a = 0.998, panel b shows a = 0.7, and panel c shows a = 0. The corresponding fixed inner disc radius Rin is stated. The solid line is the best-fitting linear regression model together with the 1σ confidence region on the model. The error bars on individual data points are 1σ (see Methods).
Extended Data Fig. 5 MCMC posterior densities for the best fitting model with parameters free.
Panel a shows the spin a, panel b shows the inner disc radius Rin, and panel c shows the inclination i. The median and 68% credible regions (equivalent to 1-sigma of a Gaussian distribution) are shown in grey vertical lines.
Extended Data Fig. 6 Scatter plots for the MCMC posterior parameter distributions.
Shown are the posteriors for spin a, inclination i, Rin, MBH, as well as source height h for two representative observations, with a low (3049) and high (3052) source flux.
Extended Data Fig. 7 The posterior parameters MBH and source height h from the model fit to just one individual lag spectra.
Panel a shows the model fit to observation 3049 and panel b that for observation 3050. The degeneracy between the model parameters can be seen. The red contours are the MCMC posteriors for the joint fit.
Extended Data Fig. 8 Modelling the rms-spectrum with the disc reflection scenario.
The solid blue lines are the model with the inclusion of the ultrafast outflow (UFO) and the dashed blue lines are without the UFO (see Methods for details). Panel a shows the ‘Broad’ rms-spectrum calculated from [0.08,6.0] x 10-4 Hz. Panel b shows the rms-spectra for a low frequency band, LF = [1.0,5.0] x 10-5 Hz. Panel c shows that of the high frequency band, HF = [4.0,20.0] x 10-4 Hz. Panel d shows the power spectral density (PSD) for the data, with the frequency ranges used for the rms-spectra indicated by the vertical solid (Broad), dashed (LF), and dotted (HF) lines. The HF band is where the reverberation signal dominates. 1σ error bars are shown on all data points.
Source data
Source Data Fig. 2
Data values for Fig. 2, ASCII.
Source Data Extended Data Fig. 1
Time lags as a function of frequency for the individual XMM-Newton observations, ASCII.
Source Data Extended Data Fig. 4
Data values for the three plots in Extended Data Fig. 4, ASCII.
Rights and permissions
About this article
Cite this article
Alston, W.N., Fabian, A.C., Kara, E. et al. A dynamic black hole corona in an active galaxy through X-ray reverberation mapping. Nat Astron 4, 597–602 (2020). https://doi.org/10.1038/s41550-019-1002-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41550-019-1002-x
This article is cited by
-
X-ray astronomy comes of age
Nature (2022)
-
Towards Precision Measurements of Accreting Black Holes Using X-Ray Reflection Spectroscopy
Space Science Reviews (2021)
-
More than softer-when-brighter: The X-ray powerlaw spectral variability in NGC 4051
Science China Physics, Mechanics & Astronomy (2020)