Abstract
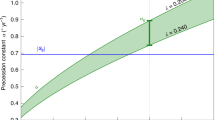
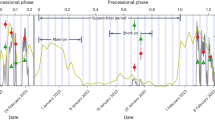
The discovery1 of 1I/2017 U1 (1I/‘Oumuamua) has provided the first glimpse of a planetesimal born in another planetary system. This interloper exhibits a variable colour within a range that is broadly consistent with local small bodies, such as the P- and D-type asteroids, Jupiter Trojans and dynamically excited Kuiper belt objects2,3,4,5,6,7. 1I/‘Oumuamua appears unusually elongated in shape, with an axial ratio exceeding 5:1 (refs 1,4,5,8). Rotation period estimates are inconsistent and varied, with reported values between 6.9 and 8.3 h (refs 4,5,6,9). Here, we analyse all the available optical photometry data reported to date. No single rotation period can explain the exhibited brightness variations. Rather, 1I/‘Oumuamua appears to be in an excited rotational state undergoing non-principal axis rotation, or tumbling. A satisfactory solution has apparent lightcurve frequencies of 0.135 and 0.126 h−1 and implies a longest-to-shortest axis ratio of ≳5:1, although the available data are insufficient to uniquely constrain the true frequencies and shape. Assuming a body that responds to non-principal axis rotation in a similar manner to Solar System asteroids and comets, the timescale to damp 1I/‘Oumuamua’s tumbling is at least one billion years. 1I/‘Oumuamua was probably set tumbling within its parent planetary system and will remain tumbling well after it has left ours.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Meech, K. J., Weryk, R. & Micheli, M. A brief visit from a red and extremely elongated interstellar asteroid. Nature 552, 378–381 (2017).
Ye, Q.-Z., Zhang, Q., Kelley, M. S. P. & Brown, P. G. 1I/2017 U1 (‘Oumuamua) is hot: imaging, spectroscopy, and search of meteor activity. Astrophys. J. Lett. 851, L5 (2017).
Fitzsimmons, A. et al. Spectroscopy and thermal modelling of the first interstellar object 1I/2017 U1 ‘Oumuamua. Nat. Astron. https://doi.org/10.1038/s41550-017-0361-4 (2018).
Bannister, M. T. et al. Col-OSSOS: colors of the interstellar planetesimal 1I/‘Oumuamua. Astrophys. J. Lett. 851, L38 (2017).
Jewitt, D. et al. Interstellar Interloper 1I/2017 U1: observations from the NOT and WIYN telescopes. Astrophys. J. Lett. 850, L36 (2017).
Bolin, B. T. et al. APO time-resolved color photometry of highly elongated interstellar object 1I/‘Oumuamua. Astrophys. J. Lett. 852, L2 (2018).
Masiero, J. Palomar optical spectrum of hyperbolic near-earth object A/2017 U1. Preprint at https://arxiv.org/abs/1710.09977 (2017).
Knight, M. M. et al. On the rotation period and shape of the hyperbolic asteroid 1I/‘Oumuamua (2017 U1) from its lightcurve. Astrophys. J. Lett. 851, L31 (2017).
Feng, F. & Jones, H. R. A. ‘Oumuamua as a messenger from the Local Association. Astrophys. J. Lett. 852, L27 (2018).
Drahus, M. et al. Tumbling motion of 1I/‘Oumuamua reveals body’s violent past. Preprint at https://arxiv.org/abs/1712.00437 (2017).
Pravec, P. et al. Tumbling asteroids. Icarus 173, 108–131 (2005).
Gutiérrez, P. J., Davidsson, B. J. R., Ortiz, J. L., Rodrigo, R. & Vidal-Nuñez, M. J. Comments on the amplitude–phase relationship of asteroid lightcurves. Effects of topography, surface scattering properties, and obliquity. Astron. Astrophys. 454, 367–377 (2006).
Zappala, V., Cellino, A., Barucci, A. M., Fulchignoni, M. & Lupishko, D. F. An analysis of the amplitude–phase relationship among asteroids. Astron. Astrophys. 231, 548–560 (1990).
Henych, T. & Pravec, P. Asteroid rotation excitation by subcatastrophic impacts. Mon. Not. R. Astron. Soc. 432, 1623–1631 (2013).
Scheeres, D. J., Ostro, S. J., Werner, R. A., Asphaug, E. & Hudson, R. S. Effects of gravitational interactions on asteroid spin states. Icarus 147, 106–118 (2000).
Samarasinha, N. H. & Mueller, B. E. A. Relating changes in cometary rotation to activity: current status and applications to Comet C/2012 S1 (ISON). Astrophys. J. Lett. 775, L10 (2013).
Vokrouhlický, D., Breiter, S., Nesvorný, D. & Bottke, W. F. Generalized YORP evolution: onset of tumbling and new asymptotic states. Icarus 191, 636–650 (2007).
Burns, J. A. & Safronov, V. S. Asteroid nutation angles. Mon. Not. R. Astron. Soc. 165, 403 (1973).
Sharma, I., Burns, J. A. & Hui, C.-Y. Nutational damping times in solids of revolution. Mon. Not. R. Astron. Soc. 359, 79–92 (2005).
Breiter, S., RoŻek, A. & Vokrouhlický, D. Stress field and spin axis relaxation for inelastic triaxial ellipsoids. Mon. Not. R. Astron. Soc. 427, 755–769 (2012).
Pravec, P. et al. The tumbling spin state of (99942) Apophis. Icarus 233, 48–60 (2014).
Scheirich, P. et al. The shape and rotation of asteroid 2008 TC3. Meteorit. Planet. Sci. 45, 1804–1811 (2010).
Engelhardt, T. et al. An observational upper limit on the interstellar number density of asteroids and comets. Astron. J. 153, 133 (2017).
Trilling, D. E. et al. Implications for planetary system formation from interstellar object 1I/2017 U1 (‘Oumuamua). Astrophys. J. Lett. 850, L38 (2017).
Grav, T. et al. The Pan-STARRS synthetic solar system model: a tool for testing and efficiency determination of the moving object processing system. Publ. Astron. Soc. Pac. 123, 423–447 (2011).
Lacerda, P., Jewitt, D. & Peixinho, N. High-precision photometry of Extreme KBO 2003 EL61. Astron. J. 135, 1749–1756 (2008).
Fraser, W. C., Brown, M. E. & Glass, F. The Hubble Wide Field Camera 3 Test of Surfaces in the Outer Solar System: spectral variation on Kuiper belt objects. Astrophys. J. 804, 31 (2015).
Jewitt, D. Color systematics of comets and related bodies. Astron. J. 150, 201 (2015).
Fukugita, M. et al. The Sloan Digital Sky Survey photometric system. Astron. J. 111, 1748 (1996).
Fraser, W. et al. TRIPPy: Trailed Image Photometry in Python. Astron. J. 151, 158 (2016).
Harris, A. W. Tumbling asteroids. Icarus 107, 209 (1994).
Acknowledgements
W.C.F., A.F., M.T.B. and P.L. acknowledge support from Science and Technology Facilities Council grant ST/P0003094/1. M.T.B. also acknowledges support from Science and Technology Facilities Council grant ST/L000709/1. The work by P.P. was supported by the Grant Agency of the Czech Republic (grant 17-00774S). C.S. is supported by a Science and Technology Facilities Council Ernest Rutherford Fellowship and grant ST/L004569/1.
Author information
Authors and Affiliations
Contributions
W.C.F. compiled the common filter dataset, re-reduced observations where necessary and led the analysis and writing of the manuscript. P.P., P. L. and I.S. performed the lightcurve modelling and assisted with writing. A.F. calculated damping timescale estimates and assisted with writing the paper. M.T.B. and C.S. assisted with interpretation of the lightcurve results and writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Table 1.
Rights and permissions
About this article
Cite this article
Fraser, W.C., Pravec, P., Fitzsimmons, A. et al. The tumbling rotational state of 1I/‘Oumuamua. Nat Astron 2, 383–386 (2018). https://doi.org/10.1038/s41550-018-0398-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41550-018-0398-z
This article is cited by
-
‘Oumuamua and meta-empirical confirmation
Foundations of Physics (2022)
-
Gaseous atomic nickel in the coma of interstellar comet 2I/Borisov
Nature (2021)
-
Tidal fragmentation as the origin of 1I/2017 U1 (‘Oumuamua)
Nature Astronomy (2020)
-
The natural history of ‘Oumuamua
Nature Astronomy (2019)
-
Tumbling motion of 1I/‘Oumuamua and its implications for the body’s distant past
Nature Astronomy (2018)