Abstract
Tetragonal CuMnAs is a room temperature antiferromagnet with an electrically reorientable Néel vector and a Dirac semimetal candidate. Direct measurements of the electronic structure of single-crystalline thin films of tetragonal CuMnAs using angle-resolved photoemission spectroscopy (ARPES) are reported, including Fermi surfaces (FS) and energy-wavevector dispersions. After correcting for a chemical potential shift of ≈− 390 meV (hole doping), there is excellent agreement of FS, orbital character of bands, and Fermi velocities between the experiment and density functional theory calculations. In addition, 2×1 surface reconstructions are found in the low energy electron diffraction (LEED) and ARPES. This work underscores the need to control the chemical potential in tetragonal CuMnAs to enable the exploration and exploitation of the Dirac fermions with tunable masses, which are predicted to be above the chemical potential in the present samples.
Similar content being viewed by others
Introduction
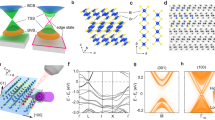
CuMnAs has emerged as an exciting material, both for spintronic applications 1,2 and the study of anti-ferromagnetic (AFM) Dirac materials3,4,5. CuMnAs has a combined inversion and time reversal symmetry, \({{{\mathcal{PT}}}}\), that connects two oppositely oriented magnetic Mn sublattices with a Néel temperature ~480 K (Fig. 1a)6,7. This \({{{\mathcal{PT}}}}\) symmetry, highlighted in Fig. 1a, in conjunction with the relativistic spin-orbit coupling allows a current to induce a non-equilibrium spin-polarization that is staggered and commensurate with the equilibrium AFM order. The non-equilibrium and equilibrium AFM moments couple to each other resulting in a spin orbit torque that reorients the Néel vector. Therefore, current driven through CuMnAs can efficiently reorient the Néel vector. This was theoretically predicted5,8 and experimentally confirmed in CuMnAs and in another \({{{\mathcal{PT}}}}\) symmetric antiferromagnet, Mn2Au1,9,10,11,12. It has also been suggested that heating effects may assist the switching by helping to overcome energy barriers12. In addition, current induced thermal gradients add not only heat but strain, which caused thermomagnetoelastic switching to dominate in an insulating AFM13. In any case, the Néel vector reorientation in CuMnAs was directly imaged using photoemission electron microscopy with x-ray magnetic linear dichroism providing contrast9.
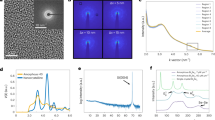
a Real space unit cell depicting the magnetic moments on the Mn atoms with arrows. b Tetragonal Brillouin zone, labeling high symmetry points. c, d LEED patterns from a decapped sample taken with 33 and 151 eV electrons, respectively. The blue diamond encloses an expected peak from tetragonal CuMnAs, while the red circles enclose extra peaks from 2×1 and 1×2 surface reconstruction domains. c The blue (red) dashed circle is drawn with a radius of \(\frac{2\pi }{a}\) (\(\frac{2\pi }{2a}\)) where a is the in-plane lattice constant of CuMnAs.
Control over the Néel vector allows manipulation of some electronic properties of CuMnAs. First, the presence of magnetic order gives rise to an anisotropic magnetoresistance (AMR). Therefore, the resistivity along the a lattice direction can be modulated by orienting the Néel vector to be perpendicular or parallel to a, for example. Wadley et al. made such a device out of a thin film of tetragonal CuMnAs and used the AMR signal to demonstrate the electrical switching of the Néel vector1. The electrical switching was even shown to be scalable to THz speeds10. However, the true origins of the observed resistance changes in similar devices has been shown to include or even be dominated by electromigration and the Seebeck effect due to large thermal gradients14,15,16. In addition, in multidomain AFMs like CuMnAs, domain migration can impact the observed changes in resistivity due to domain wall magnetoresistance17. Second, the \({{{\mathcal{PT}}}}\) symmetry provides doubly degenerate bands, which allows for the existence of antiferromagnetic Dirac fermions close to or at the Fermi level5. Additional off-centered or nonsymmorphic crystallographic symmetries can protect the massless Dirac fermions. The presence or absence of these symmetries can be controlled by reorienting the Néel vector resulting in tunable masses of the Dirac fermions. The opening and closing of the Dirac mass gap results in enhancement of the AMR5,11.
Both the tetragonal and orthorhombic phases of CuMnAs have been studied theoretically and experimentally. All of the above interesting properties are believed to be present in both structural phases. In addition, the orthorhombic phase is proposed to host a topological metal-insulator transition, due to the predicted presence of a bulk Dirac point at EF and lack of other bands crossing EF5.
Density Functional Theory (DFT) has been critical to the development of the above theoretical predictions, but it has only been experimentally tested to a limited extent in tetragonal CuMnAs: the AC permittivity (determined from ellipsometry) and UV photoemission spectroscopy were studied18; neutron diffraction and x-ray magnetic linear dichroism were used to study the magnetic ordering19; and, more recently, experiments using scanning tunneling microscopy elucidated the surface termination of thin films of tetragonal CuMnAs, discovering the existence of As step edges which may host surface reconstructions20. These experiments were compared to DFT predictions; however, there exist no direct comparisons to the band structure calculated from DFT.
We directly measure the band structure with high resolution ARPES measurements and provide a detailed comparison to DFT. In addition, we find surface reconstructions and a chemical potential shift.
Results
Theory
We show the crystallographic and magnetic structure of tetragonal phase of CuMnAs in Fig. 1a. The nonmagnetic space group is nonsymmorphic (P4/nmm). Since the magnetic Mn atoms are light, the effects of spin-orbit coupling on the band-structure are highly perturbative and smaller than our resolution can detect, unlike in strongly relativistic \({{{\mathcal{PT}}}}\) antiferromagnet Mn2Au21. Therefore, in the antiferromagnetic state the nonrelativistic spin group (P14/2n2m2m) describes the main energy scales of our measured band structure, including Fermi surfaces22. However, within ~10 meV of a Dirac point, the fermion masses are required to accurately describe the electronic dispersion, and to calculate the Dirac fermion masses, spin-orbit coupling must be included and the relativistic magnetic symmetry group (Pm’mn) with generators \(\{{C}_{2x}| \frac{1}{2}00\}\), \(\{{M}_{y}| 0\frac{1}{2}0\}\), and \({{{\mathcal{PT}}}}\) must be employed.
To model the electronic structure of tetragonal CuMnAs, DFT was performed, using the Generalized Gradient Approximations (GGA) with the Coulomb interaction U applied to the Mn 3d orbitals, using Dudarev’s implementation23,24,25 (see “Methods” for a complete description of our DFT). For the reasons stated above, spin-orbit coupling was turned off for all DFT shown, except Fig. 4a–c and Supplementary Figure 2. The best quantitative agreement of Fermi velocities was found for U = 2.25 eV, while maintaining excellent overall qualitative agreement. It was necessary to apply ≈390 meV of rigid hole doping to the chemical potential from theory, i.e. the experimental Fermi energy was found to be equal to the theoretical Fermi energy − 390 meV. Possible origins of the energy shift will be discussed. Therefore, unless explicitly discussed, all of the DFT shown in this manuscript has been plotted after applying the above mentioned rigid chemical potential shift.
LEED
After decapping, LEED was performed in situ, revealing a well-ordered surface with reconstructions (Fig. 1c, d). The (001) surface of tetragonal CuMnAs should produce a square reciprocal lattice with edge lengths of 2π/a, where a is determined from XRD to be 3.85 Å. This is seen in the LEED patterns; however, there are additional spots at the midpoints along the edges of the squares, suggesting the presence of 2×1 and 1×2 surface reconstruction domains. The reconstruction is confirmed by observing that the first order Bragg peaks occur at a radius of 2π/2a, where without a reconstruction they would occur at 2π/a (Fig. 1c). Despite the surface reconstruction, the LEED pattern is sharp, indicating a successful decap. Samples were subsequently transferred into the ARPES chamber, maintaining an ultra-high vacuum environment from decap to ARPES data acquisition.
ARPES and DFT comparison
As a first step to understanding the electronic structure of tetragonal CuMnAs, the in-plane Fermi surface was measured at kz ≈ 0 (Fig. 2c) and kz ≈ π/c (Fig. 2d), which may be selected by tuning the photon energy (see Supplementary Note 3). In this case, the zone center data were taken with 85 eV photons, whereas the zone edge data were taken at 100 eV. For comparison, the undoped and doped Fermi surfaces from the DFT are shown in Fig. 2a, b, respectively. It is clear that the undoped Fermi surface does not agree with experiment. For example, there are no pockets near the M points. However, after lowering the chemical potential of the DFT by ≈0.390 eV (rigid hole doping), all of the qualitative and even quantitative features of the experimental Fermi surface are consistent with the bulk DFT calculations. To illustrate the qualitative agreement, the hole-doped Fermi surface is overlaid on the data in Fig. 2e, f. They both show a propeller-shaped Fermi surface in the kz ≈ 0 plane and ellipses at the R points in the kz ≈ π/c plane, with the experiment and theory displaying a very similar shape and size of these features. There are, however, three subtle effects that might naively appear as qualitative discrepancies between the experiment and theory: First, unlike the DFT, the data shown in Fig. 2d, f does not have C4 symmetry. While turning on spin-orbit coupling in the DFT would break this symmetry, the affect is too small to explain the data or even detect (see Supplementary Note 2 for Fermi surfaces with spin-orbit coupling included). Instead, it is primarily the transition matrix element that is known to modulate the ARPES spectral intensity that is responsible for breaking the C4 symmetry in the data. In fact, a detailed analysis of this matrix element effect reveals the orbital character of the Fermi surface, which is in good agreement with that of the DFT (see Supplementary Note 4). Second, due to the inherent surface sensitivity of ARPES and lack of translational symmetry perpendicular to the surface, ARPES spectra from any photon energy can contain contributions from multiple kz values. This explains the closed ellipses near the X points in Fig. 2c and some of the weight at kx = 0 near the Z point in Fig. 2d. This point is visually illustrated in Fig. 2e by overlaying the DFT from a second kz value (orange transparency) that is 0.35π/c away from the anticipated kz value (red transparency). Third, there is extra spectral weight near the Z point in Fig. 2f indicated by white text, which is identified as a replica of the vertical ellipses enclosing the zone edges at kx = 0. The back-folding of this ellipse onto Z is the analogue of the 2×1 surface reconstructions observed in the LEED and will be analyzed quantitatively later.
a, b 3D Fermi surfaces from the DFT plotted with PyProcar32: a undoped and b hole doped. Unsymmetrized Fermi surface data taken with 85 eV (c, e) and 100 eV (d, f), linear vertically polarized photons. c–f The same data is shown twice. The black box depicts the Brillouin zone boundary. The data is from the CuMnAs01 sample. e, f Because the undoped DFT does not match the experimental data, the hole doped DFT is overlaid with a transparency. The insets show only the hole doped DFT.
With the aid of Fermi surface plots and kz dispersion (see Supplementary Note 3), E-k dispersion for the high symmetry cuts in the Γ-X plane are readily acquired using 85 eV, LV polarized photons (Fig. 3a, f). To quantitatively compare the experimental data to DFT, momentum distribution cuts (MDCs) are fit (Fig. 3c, e) to extract the low energy experimental dispersion, which is overlaid with corresponding dispersions from the hole doped DFT in Fig. 3b, d. In addition, the MDC peak locations may be fit to a line to extract the Fermi velocity. The X → Γ → X MDCs are fit with two Voigt functions, and the extracted Fermi velocity is 4.6 eV Å, which to within the experimental error bars is the same as the Fermi velocity from the hold doped DFT, vF = 4.8 eV Å. The M → X → M symmetry cut contains the A → R → A bands near EF, due to the same kz uncertainty mentioned above. Therefore, the extracted MDCs were fit with four Voigt functions, representing four bands. The Fermi velocity of the bands corresponding to the M → X → M cut is 6.0 eV Å. Again to within experimental precision, this is the same as the Fermi velocity from the hole doped DFT, vF = 6.4 eV Å. The error on the extracted Fermi velocities from MDC fittings scales as \(\sim {{v}_{{{{\rm{F}}}}}}^{2}\). So, for these large Fermi velocities, the relative error is found to be ~10% (see Supplementary Note 6). To see the full ARPES images for several high symmetry cuts along with a matrix element analysis of the cuts shown, see Supplementary Note 5.
a, f ARPES images with hole doped DFT overlaid as dashed lines. Black boxes in (a) and (f) depict the region shown in (b, c) and (d, e), respectively. b, d Comparison of the dispersion from the hole doped DFT and experiment. c, e Waterfall plots of MDCs with fits overlaid. Upper panels depict a single MDC, highlighting the individual Voigt functions used for each peak in the fit. a–f The X → Γ → X and M → X → M symmetry cuts--(a–c) and (d–f), respectively--were acquired with 85 eV, LV polarized photons. The X → Γ → X data comes from the CuMnAs01 sample and the M → X → M data from the CuMnAs02 sample.
Much of the interest in CuMnAs stems from the predicted Dirac fermions with an electrically tunable mass gap. After tuning the DFT to match the experimental data, these Dirac crossings are still present and with the addition of spin-orbit coupling exhibit the changing Dirac fermion masses (Fig. 4a–c). There are Dirac crossings deep below the Fermi energy that were studied. Figure 4d shows data along the M → X → M edge of the Brillouin zone taken with 100 eV LV photons with hole doped DFT overlaid. However, because the Dirac points are so deep in binding and the data is broadened in kz due to surface sensitivity, the Dirac points cannot be resolved to compare directly to the DFT. Nevertheless, the qualitative agreement is strong. This raises the confidence in the existence of the Dirac crossings only 180 meV above the stoichiometric and defect-free Fermi energy (see the red circle in Fig. 4b). Note, moving EF to this Dirac point should enable band topology switching. In addition, this would enable electrically controllable anisotropic changes in the DOS near EF, which one would expect to produce a larger AMR signal than the traditional type that depends on anisotropic scattering rates. Indeed, anisotropic changes in the band gap of EuMnSb2 played a crucial role in the discovered colossal AMR signal26.
a Shows the Y → M → X cut near EF from DFT on the undoped energy scale with spin-orbit coupling included. b, c Zoom in on the dispersion in the red and green boxes shown in (a), respectively, highlighting nearby Dirac fermions. The red circle in (b) shows the closest Dirac point to EF. d ARPES image with hole doped DFT overlaid. Data comes from the CuMnAs01 sample, which has AFM domains with the Néel vector along [1, 1, 0] and \([1,\bar{1},0]\). The black circles highlight the same Dirac points in both (c, d).
More generally, the strong agreement between the DFT and experiment shown throughout this paper lend credence to the predictions from the DFT beyond the ones directly verified. For example, this applies to the atomic character of the bands predicted by the DFT (see Supplementary Note 1).
Having demonstrated the strong agreement between the DFT and experiment, it is time to address two issues raised previously in detail-the replication and doping. First, to quantitatively test the hypothesis that the extra structure near the Z point of the Fermi surface is the replication of the ellipses near the R point (Fig. 5a), the dispersion along the R → Z → R cut is compared to the dispersion along the A → R → A cut. MDC fitting is used to extract the experimental dispersion along the R → Z → R cut (Fig. 5b). The MDCs are fit with three Voigt functions-two to capture the bands in question and one to capture a band top at kx = 0 that disperses across EF as a function of kz. The extracted dispersion from the R → Z → R cut is overlaid with the DFT dispersion along the A → R → A cut, showing excellent qualitative agreement (Fig. 5c). From MDC analysis, the Fermi velocity of the bands in the R → Z → R cut is determined to be 5.1 eV Å. The Fermi velocity of the A → R → A cut extracted from the DFT is 5.2 eV Å, which is within 2% of the experimental value.
a The same Fermi surface data as shown in Fig. 2b. The blue dashed ellipse represents a primary pocket that replicates as the red dashed ellipse due to the 1×2 surface reconstructions. b Waterfall plot of MDCs extracted from the R → Z → R symmetry cut [red line in (a)]. c Comparison of the experimental R → Z → R dispersion and the A → R → A dispersion from the DFT. The blue line in (a) shows the A → R → A symmetry cut.
Second, to determine if the ≈390 meV chemical potential shift is reasonable, necessary concentrations of likely defects are calculated. It turns out that two effects allow this relatively large energy shift to be explained by reasonably small defect concentrations. First, CuMnAs is a semimetal. According to the DFT, ≈390 meV of hole doping corresponds to only 0.27 holes per unit cell. Second, the most likely defects all bring a substantial number of holes with each defect. According to Máca et al., the most energetically favorable defects are Cu and Mn vacancies followed by Mn substitutions for Cu27. One reasonably suspects that the non-magnetic copper will have 10 valence electrons, i.e., will be [Ar] 3d10, and the magnetic Mn will be [Ar] 3d5 with 5 valence electrons, naively leaving As with a full valence shell. The atomically projected Density Of States (DOS) from the DFT mostly agrees with this intuition, finding 10 valence electrons on Cu and 5.4 on Mn, which would mean that each Mn for Cu substitution brings 4.6 holes. Therefore, taking into account the 222 stoichiometry of the unit cell, the 388 meV shift would result from only 1.3%, 2.4%, and 2.9% of pure Cu or Mn vacancies or Mn for Cu substitutions, respectively. Furthermore, there could be combinations of these defects, yielding very reasonable defect levels. Specifically, the defect concentrations in the few percent range give, according to Máca et al.27, DFT resistivities of CuMnAs consistent with experiment.
Discussion
The electronic structure of tetragonal CuMnAs is measured with ARPES, and in-plane Fermi surfaces, kz dispersions (see Supplementary Note 3), and E vs. k symmetry cuts are reported. After shifting the chemical potential by ≈− 390 meV (hole doping), DFT calculations-using GGA+U with U = 2.25 eV applied to the Mn-3d orbitals-are found to be in excellent qualitative and quantitative agreement with the experimental data. In particular, the DFT predicts accurate Fermi velocities and an orbital character for the bands that is consistent with the experimental results. In addition, surface reconstruction and replicated bands are found.
Furthermore, the extracted value of U is consistent with that of other studies. Veis et al. found that Ueff = (U − J) ≈ 2 eV fit their angle-integrated photoemission data best18. In the GGA+U scheme used for the calculations in this paper, U and J values are not separate, and what really enters the total energy is the “U − J” value. So, the U = 2.25 eV term in this manuscript corresponds to the Ueff. Guyen et al. used U = 2 eV to explain emergent edge states on their surface reconstructed CuMnAs thin films20. U < 2 eV fails to even qualitatively capture the ARPES experimental results, primarily because the bandwidth of the band in the X → Γ → X is too small. The strongly constrained and appropriately normed (SCAN) functional28 increased this bandwidth compared to pure GGA, yielding a similar bandwidth to U = 1 eV. Nevertheless, SCAN still did not produce a large enough bandwidth for the X → Γ → X cut. U = 2.25 eV within GGA was primarily chosen because it reproduces the Fermi velocity in the X → Γ → X cut most accurately.
By showing that DFT accurately captures the electronic structure of tetragonal CuMnAs, more weight is given to the growing interest in CuMnAs as a candidate AFM topological Dirac material. Furthermore, the low DOS near EF provides hope that tetragonal CuMnAs can be electron doped moving EF into the proximity of the electrically switchable Dirac points above EF in the studied films. According to the DFT, the Dirac points are 570 meV or ~0.38 electrons per unit cell above the chemical potential in the current films or only 180 meV/~0.12 electrons per unit cell above the defect free chemical potential. Alternatively, orthorhombic CuMnAs was suggested to be a pristine antiferromagnetic Dirac semimetal with only Dirac fermions at the Fermi level without any trivial bands. Considering the reliability of DFT in the description of tetragonal CuMnAs presented here, studying orthorhombic CuMnAs appears as a promising direction in research of antiferromagnetic Dirac semimetals.
Methods
ARPES
High resolution ARPES measurements were made at the MERLIN ARPES endstation of beamline 4.0.3 at the Advanced Light Source and at the HR-ARPES branch of beamline i05 at the Diamond Light Source. Data were taken below 50 K with photon energies in the range 75–125 eV, using both linear vertical and linear horizontal polarization. The base pressure was ≲5 × 10−11 Torr.
Sample preparation
The 45 nm thick films of single-crystalline tetragonal CuMnAs were grown by molecular beam epitaxy on GaP(001) with the (001) face of CuMnAs exposed. The films were capped with 30 nm of As to protect the surfaces from contamination from the ambient environment. Decapping was performed in an environment with pressures ≲ 10−8 Torr, reaching a max temperature reading of 340 ∘C on a pyrometer, emissivity = 0.1.
Density functional theory calculations
The DFT calculations were performed with Vienna Ab-initio Simulation Package (VASP)23,24,25, based on a plane wave basis set. The interaction between ions and electrons is described by the projector-augmented wave (PAW) method29,30. GGA+U scheme was applied, with the exchange-correlation functional being the Perdew-Burke-Ernzerhof generalized gradient approximation functional31, and an on-site Coulomb potential of 2.25 eV was applied to the Mn-3d electrons, using Dudarev’s implementation. A full relaxation of the lattice structure was carried out with the energy and force breaking condition set to 10−6 eV and 10−3 eVÅ−1. The cut off energy was taken as 550 eV. A dense k-mesh of 31*31*19 was used in the static calculation of the electronic structure. The calculations were carried out with each of the Mn atoms having a magnetic moment of 3.67 μB with the Néel vector along the [010] orientation. Finally, the chemical potential was shifted to bring the band top at Z in the DFT to the corresponding maximum intensity in the experimental Energy Dispersion Cut (EDC) through Z. In the case of U = 2.25 eV, this was 388 meV, but the precise shift did depend on the specific value of U used, with all U values requiring some shift.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code used in this work are available from the corresponding author upon reasonable request.
References
Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 587–590 (2016).
Stamenova, M., Mohebbi, R., Seyed-Yazdi, J., Rungger, I. & Sanvito, S. First-principles spin-transfer torque in CuMnAs∣GaP∣CuMnAs junctions. Phys. Rev. B 95, 060403 (2017).
Šmejkal, L., Mokrousov, Y., Yan, B. & MacDonald, A. H. Topological antiferromagnetic spintronics. Nat. Phys. 14, 242–251 (2018).
Tang, P., Zhou, Q., Xu, G. & Zhang, S.-C. Dirac fermions in an antiferromagnetic semimetal. Nat. Phys. 12, 1100–1104 (2016).
Šmejkal, L., Železný, J., Sinova, J. & Jungwirth, T. Electric control of dirac quasiparticles by spin-orbit torque in an antiferromagnet. Phys. Rev. Lett. 118, 106402 (2017).
Wadley, P. et al. Tetragonal phase of epitaxial room-temperature antiferromagnet CuMnAs. Nat. Commun. 4, 2322 (2013).
Máca, F. et al. Room-temperature antiferromagnetism in CuMnAs. J. Magn. Magn. Mater. 324, 1606–1612 (2012).
Železný, J. et al. Relativistic Néel-order fields induced by electrical current in antiferromagnets. Phys. Rev. Lett. 113, 157201 (2014).
Grzybowski, M. et al. Imaging current-induced switching of antiferromagnetic domains in CuMnAs. Phys. Rev. Lett. 118, 057701 (2017).
Olejník, K. et al. Terahertz electrical writing speed in an antiferromagnetic memory. Sci. Adv. 4, eaar3566 (2018).
Bodnar, S. Y. et al. Writing and reading antiferromagnetic Mn2Au by Néel spin-orbit torques and large anisotropic magnetoresistance. Nat. Commun. 9, 348 (2018).
Meinert, M., Graulich, D. & Matalla-Wagner, T. Electrical switching of antiferromagnetic Mn2Au and the role of thermal activation. Phys. Rev. Appl. 9, 064040 (2018).
Meer, H. et al. Direct imaging of current-induced antiferromagnetic switching revealing a pure thermomagnetoelastic switching mechanism in NiO. Nano Lett. 21, 114–119 (2021).
Chiang, C., Huang, S., Qu, D., Wu, P. & Chien, C. Absence of evidence of electrical switching of the antiferromagnetic Néel vector. Phys. Rev. Lett. 123, 227203 (2019).
Zhang, P., Finley, J., Safi, T. & Liu, L. Quantitative study on current-induced effect in an antiferromagnet insulator/Pt bilayer film. Phys. Rev. Lett. 123, 247206 (2019).
Churikova, A. et al. Non-magnetic origin of spin Hall magnetoresistance-like signals in Pt films and epitaxial NiO/Pt bilayers. Appl. Phys. Lett. 116, 022410 (2020).
Bodnar, S. Y. et al. Magnetoresistance effects in the metallic antiferromagnet Mn2Au. Phys. Rev. Appl. 14, 014004 (2020).
Veis, M. et al. Band structure of CuMnAs probed by optical and photoemission spectroscopy. Phys. Rev. B 97, 125109 (2018).
Wadley, P. et al. Antiferromagnetic structure in tetragonal CuMnAs thin films. Sci. Rep. 5, 17079 (2015).
Nguyen, G. D. et al. Emerging edge states on the surface of the epitaxial semimetal CuMnAs thin film. Appl. Phys. Lett. 116, 061603 (2020).
Fedchenko, O. et al. Direct observation of antiferromagnetic parity violation in the electronic structure of Mn2Au. J. Condens. Matter Phys. 34, 425501 (2022).
Šmejkal, L., Sinova, J. & Jungwirth, T. Beyond conventional ferromagnetism and antiferromagnetism: a phase with nonrelativistic spin and crystal rotation symmetry. Phys. Rev. X 12, 031042 (2022).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Sun, Z. L. et al. Field-induced metal-to-insulator transition and colossal anisotropic magnetoresistance in a nearly Dirac material EuMnSb2. npj Quantum Mater. 6, 94 (2021).
Máca, F. et al. Physical properties of the tetragonal CuMnAs: a first-principles study. Phys. Rev. B 96, 094406 (2017).
Sun, J., Ruzsinszky, A. & Perdew, J. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 115, 036402 (2015).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Herath, U. et al. PyProcar: a python library for electronic structure pre/post-processing. Comput. Phys. Commun. 251, 107080 (2020).
Acknowledgements
This work was supported by DOE grant DE-FG02-03ER46066, Betty and Gordon Moore Foundation grant GBMF9458, Ministry of Education of the Czech Republic Grants LNSM-LNSpin, LM2018140, Czech Science Foundation Grant No. 19-28375X, and EU FET Open RIA Grant No. 766566. In addition, P. Wadley acknowledges support from the Royal Society through a Royal Society University Research Fellowship. This research used resources of the Advanced Light Source, a U.S. DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. We would like to thank the Diamond i05 ARPES (SI22665, SI24224-1) and ALS Merlin ARPES end station teams for allowing us time for and aiding in the ARPES data acquisition.
Author information
Authors and Affiliations
Contributions
A.G.L. and K.N.G. contributed equally to gathering the ARPES data with support from J.D.D., P.H., B.S.B., D.N., T.K., C.C., N.S., S.R., and S.D. The DFT shown in this paper was performed by P.H. with feedback from A.G.L., D.D., L.Š., and T.J. P.W. oversaw the growth and characterization of the thin films of tetragonal CuMnAs by R.P.C. and V.N. This manuscript was prepared by A.G.L. under guidance from D.D. and with feedback from all authors. D.D. was the principal investigator overseeing the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Linn, A.G., Hao, P., Gordon, K.N. et al. Experimental electronic structure of the electrically switchable antiferromagnet CuMnAs. npj Quantum Mater. 8, 19 (2023). https://doi.org/10.1038/s41535-023-00554-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-023-00554-x