Abstract
Spin–orbit coupling forms the physical basis for quantum materials with non-trivial topology and potential spintronics applications. The Rashba interaction is a textbook model of spin–orbit interactions, with charge carriers undergoing linear, isotropic spin-splitting in momentum space. Recently, non-centrosymmetric semiconductors in the family BiTeX (X = Cl, Br, I) have been identified as exemplary Rashba materials due to the strong splitting of their bulk bands, yet a detailed investigation of their spin textures, and their relationships to local crystal symmetry, is currently lacking. We perform high-efficiency spin-resolved photoemission spectroscopy to directly image the spin texture of surface states of BiTeCl, and we find dramatic deviations from idealized behavior, including a reversal of the spin-polarization near the Fermi level. We show that this behavior can be described by higher-order contributions to the canonical Rashba model with the surface states localized to individual trilayers of the crystal. Due to the prominence of these effects near the Fermi level, they should have a strong impact on the spin-dependent transport of carriers.
Similar content being viewed by others
Introduction
The spin–orbit interaction features prominently in contemporary research of quantum materials. On the one hand, it can impart a geometrical phase to electron wavefunctions to endow materials with non-trivial topological properties1,2,3. On the other, it affords a physical mechanism for spintronics applications which seek to control the electron’s spin degree-of-freedom without magnetic fields4,5,6. Therefore, intensive investigation of spin–orbit interactions is of central importance to the development of new classes of topological materials and the implementation of practical spintronics.
A textbook example of spin–orbit interactions is provided by the Rashba interaction, described by the well-known Hamiltonian7:
where σ and k are the electron spin and momentum, respectively, and \(\hat{{{{\bf{z}}}}}\) is a unit vector along the surface normal. Intuitively, this describes a linear band splitting with the orientations of σ and k locked orthogonally, with the Rashba parameter α determining the magnitude of the splitting. Recently, non-centrosymmetric semiconductors in the family BiTeX (X = Cl, Br, I) have been shown to exhibit sizeable values of α in their bulk and surface bands, exceeding that of traditional semiconductors by 1–2 orders of magnitude8,9,10,11. Angle-resolved photoemission spectroscopy (ARPES) has proven to be an invaluable tool for characterizing the electronic structure of both bulk and surface states12,13,14,15, with spin-resolved ARPES verifying the existence of spin-momentum locking and thereby supporting the Rashba picture8,16,17,18,19. An open issue is whether these states are better described as delocalized quantum well states or as surface states localized to individual trilayers10,14,16,17, and it has been argued that there is little practical difference from an ARPES standpoint15.
In this Article, we perform spin-resolved ARPES on BiTeCl to study the spin-polarization of the surface charge carriers near the Fermi level EF. The high efficiency of our measurement allows us to densely sample the band structure in energy and momentum, from which we can directly image dramatic deviations from the ideal Rashba spin texture, including a reversal of the in-plane spin-orientation. We show that this behavior follows from higher-order corrections to the canonical Rashba Hamiltonian, and based on arguments exploiting the crystal symmetry of BiTeCl, we conclude that the states are localized to individual trilayers. These deviations are prominent near EF, and thus should have a strong impact on the transport of charge carriers. More generally, our findings highlight the interplay between electron wavefunctions, local crystal symmetries, and higher-order spin–orbit effects, which is vital when assessing the suitability of materials for topological or spintronic applications.
Results
Spin-integrated electronic structure
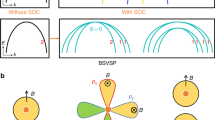
The crystal structure of BiTeCl is shown on the left side of Fig. 1a. It is noteworthy that BiTeCl belongs to the space group P63mc in contrast to BiTeBr and BiTeI, which belong to P3m120. The latter two consist of stacked trilayers, with each individual trilayer (and hence the entire lattice) exhibiting 3m symmetry. While the individual trilayers of BiTeCl locally exhibit 3m symmetry, the lattice itself exhibits 6mm symmetry due to 60∘ rotation between neighboring trilayers.
a Crystal structure and schematic of the bands localized near the Te-terminated surface due to a depth-dependent potential V(z). Each sub-band shows a Rashba-like spin splitting. b, c Spin-integrated ARPES measurements of the Te-terminated surface along Γ-K and Γ-M, respectively, revealing the sub-band structure.
The lattice of BiTeCl cleaves between Te and Cl planes, resulting in surfaces of opposite polarity. In a single domain crystal, this termination follows deterministically from the orientation of the non-centrosymmetric crystal rather than from a stochastic cleavage process10,13,15. The band-bending potential V(z) splits off surface sub-bands, each of which undergoes spin-splitting, as sketched in the right side of Fig. 1a. In this paper we focus on the Te-terminated surface, since its surface sub-band at the deepest binding energy has been identified as a potentially ideal Rashba system due to its predicted strong splitting, isotropic dispersion, and energetic separation from bulk states10.
Our ARPES measurements along the Γ-K and Γ-M directions are shown in Fig. 1b, c, respectively. Comparison of the two spectra indicates that the band dispersions are largely isotropic, with a notable exception for the bands from the outermost sub-band pair, which linearly cross EF along Γ-K but merge into each other along the Γ-M direction. These observations are consistent with ARPES results in the literature, which have identified the dispersions with a Rashba spin texture8,12,13,14,15,16,17,18,19.
Spin-resolved electronic structure
To investigate the associated spin structure in detail, we performed spin-resolved ARPES in the geometry shown in Fig. 2a. The measured in-plane spin-polarization along Γ-K and Γ-M is represented in a 2-dimensional colorscale in (b) and (d), respectively. In (c) and (e) we extract the spin-up I↑ and spin-down I↓ intensities, plotted as normalized momentum distribution curves (MDCs), with triangles inserted as guides to the eye to denote the peak positions of the outermost sub-band pair.
a A schematic of the experimental geometry. Momentum-dependence is mapped by rotating the sample angle θ. Data in this figure is obtained with s-polarized light. Images are plotted with a 2D colorscale shown in the upper-right: red-blue (vertical) denotes spin-polarization and white-black (horizontal) denotes photoemission intensity. b An in-plane (Sy) measurement along Γ-K. An unexpected reversal of the spin-polarization is seen in the outermost bands near EF (beige arrows). c The corresponding momentum distribution curves (MDCs) of spin-up I↑ and spin-down I↓ intensities. Each MDC is integrated within an energy window of 34 meV. Altogether, the MDCs span the energy range from −329 to 41 meV as denoted by the double-arrows in (b). Each I↑↓ pair is normalized by the maximum intensity for that pair to facilitate a comparison between MDCs at different energies. The markers are guides to the eye denoting peak positions, with blue-black-red coloring indicating the overall polarization of each peak. d, e An analogous dataset along Γ-M, in which the outermost bands merge into a single unpolarized peak near EF.
The overall spin-polarization behavior indicates that each sub-band independently undergoes spin-splitting, as suggested in Fig. 1a. However, closer examination reveals a discrepancy from the Rashba model: the spin-polarization along Γ-K abruptly reverses sign in the outermost sub-band near EF. This anomaly is clearly observed at k ≈ ± 0.2 Å−1 in both the image plot as well as the MDCs. The Γ-M data, however, simply shows the two bands merging into a single peak above EF.
Next, we performed band structure calculations of a 20 trilayer slab constructed with a band-bending potential. The spin-resolved band structure of the top ten Te-terminated surface layers is plotted along both Γ-K and Γ-M in Fig. 3. The colors in the top row (bottom row) denote in-plane (out-of-plane) spin polarization. Though there are some discrepancies in the details of the dispersions, these calculations support the most noteworthy experimental observations—namely, the polarization reversal of the outermost band along Γ-K and the merging of the two bands along Γ-M. This comparison confirms that our observations are rooted in the material’s physics rather than an extrinsic artifact associated with the photoemission process. The calculations also show that an out-of-plane spin texture develops along Γ-K but not Γ-M.
Higher-order Rashba model
To gain a deeper understanding of our experimental data, we seek a mechanism for the peculiar behavior of the spin-texture based on higher-order contributions to the Rashba Hamiltonian. These have functional forms which depend on the crystal symmetry21, and it is unclear whether the threefold symmetry of the individual trilayers (3m) or the six-fold symmetry of the entire crystal (6mm) should be applied. To address this question, we use our band structure calculations to plot the spatial extent of the surface state wavefunctions in Fig. 4a. The two lowest-energy states are largely localized to individual trilayers, as also supported by Fig. 4b, c, in which the colorscale encodes the projection into the first and second trilayers, respectively. Due to the high degree of localization, we adopt the Rashba terms with threefold symmetry to describe the surface states21:
where kx (ky) is in the Γ-K (Γ-M) direction, and γ1 and γ2 represent the interaction strengths for in-plane and out-of-plane spin components, respectively. Note that the first term can be written as \(-{\gamma }_{1}| {{{\bf{k}}}}{| }^{2}({{{\boldsymbol{\sigma }}}}\,\times\, {{{\bf{k}}}})\,\cdot\, \hat{{{{\bf{z}}}}}\) which has the same symmetry as the first-order term (Eq. 1) and thus maintains an isotropic band dispersion with a helical in-plane spin texture. In contrast, the second term has threefold symmetry and introduces anisotropic band warping together with an out-of-plane spin component. Note that six-fold symmetry would require that the second term vanish (γ2 = 0), and only the isotropic terms would remain. As we shall see, this term is essential for describing the experimental data and theoretical calculations, which provides further evidence for the applicability of threefold symmetry.
From Eq. 2 we can immediately make a few salient observations: (1) If α and γ1 have opposite signs, the splitting vanishes at \({k}_{y}\,=\,\pm {k}^{* }\,\equiv\, \pm \sqrt{-\alpha /{\gamma }_{1}}\). (2) At kx = ± k*, this degeneracy is lifted by the γ2 term, which rotates the spin out-of-plane. (3) Beyond k*, the cubic γ1 term overtakes the linear α term, resulting in a reversal of the in-plane spin texture. Figure 5 presents a comprehensive comparison between a model constructed by including the cubic terms (see Supplementary Note 7) and our experimental data. First, the difference in the constant-energy contours between the linear and cubic models is highlighted in (a). Next, in Fig. 5b we examine the in-plane spin along the Γ-M direction. The model (right) shows the splitting vanishing at ± k* ≈ 0.2 Å−1, but with otherwise no perturbation to the in-plane spin texture, consistent with the data (left). At the same time, Fig. 5d shows that there is no out-of-plane component of the spin-polarization in both the experiment and theory, in agreement with the band structure calculations, and as required by symmetry22.
a Representative constant-energy contours of the linear and cubic Hamiltonians. b, c Comparison between experiment (measured with p-polarized light) and the cubic Rashba model for the in-plane spin component along Γ-M and Γ-K, respectively. d, e Same, but for the out-of-plane spin component. f, g Quantitative comparison between the experimentally-measured spin-polarization and the results of the third-order Rashba model along Γ-K for in-plane and out-of-plane spins, respectively. Each spin-polarization curve is extracted by integrating an energy window of ±45 meV along the outermost sub-bands, as indicated by the guides to the eye in (c). In addition to the plotted statistical error bars, we estimate a fractional systematic uncertainty in the measured spin-polarization of ±10%. An energy-dependent signal-to-background ratio is incorporated into the model to permit a direct comparison with the data (see Supplementary Note 9).
Now we consider the Γ-K direction, as shown in Fig. 5c, e. Due to the γ2 term, the bands are split at ±k* and both disperse linearly near EF. Most importantly, the model shows the in-plane spin-polarization reversing sign as the band disperses beyond k*, as in the experiment. Finally, because the γ2 term is associated with σz, there should be an out-of-plane spin component along the Γ-K direction, as predicted in the band structure calculations, and similarly observed experimentally in Fig. 5e. We also note that the 60∘ rotation between adjacent trilayers in BiTeCl should cause γ2 to reverse sign for the states localized to those layers. This would have no signature in the band dispersion, but would cause a reversal in the out-of-plane spin texture. This effect cannot be observed experimentally since the relevant states are above EF, but it is clearly present in the lower-left panel of Fig. 3 (see orange circled regions).
As a final layer of complexity, we note that our dataset reveals a spin-orbital texture. This is manifested as the reversal of all spin-polarizations between Fig. 2, which was measured with s-polarized light, and Fig. 5, which was measured with p-polarized light. This type of spin-orbital texture is consistent with previous work on topological insulators23,24,25,26,27,28, Rashba-split quantum well states29, and the related material BiTeI18, and can be readily incorporated into the third-order Rashba model (see Supplementary Note 8). Differences in the appearance of the reversal near EF are attributed to polarization-dependent matrix elements, as described in Supplementary Note 1130.
For a quantitative comparison, in Fig. 5f, g we overlay the measured spin-polarizations (magenta dots) with predictions from the cubic Rashba model (dashed gray lines). There is a substantial discrepancy, especially for smaller k, which can be readily understood as follows: the bands’ measured spectral-weight diminishes with binding energy, possibly due to matrix element or self-energy effects. Together with an unpolarized background intensity, this results in a suppression of the measured spin-polarizations near the Γ-point. To facilitate a one-to-one comparison, we incorporate a similar spectral-weight suppression into the cubic Rashba model—with a constant unpolarized background—and plot the modified model’s results using wide magenta lines (see Supplementary Note 9). We observe an overall agreement, despite the simplicity of this model. Though the out-of-plane spin of the inner band shows a discrepancy, we speculate that this may be associated with factors beyond the model, such as atom-dependent orbital textures31, photoemission matrix elements32, or overlapping spectral-weight from adjacent sub-bands.
Discussion
This work demonstrates that a cubic Rashba Hamiltonian with threefold (3m) symmetry provides an excellent description for the spin–orbit physics of the surface states of BiTeCl. The two key observations are (1) the anisotropic band dispersion, with a spin-degeneracy at k* along Γ-M being split along Γ-K; and (2) the associated out-of-plane spin components along Γ-K which are absent along Γ-M. Both of these signatures are present in experimental spin-resolved ARPES measurements as well as band structure calculations. In addition, the calculations show that the out-of-plane spin texture reverses sign between consecutive sets of surface states. This is due to the 60∘ rotation between adjacent trilayers of BiTeCl, which gives rise to the global six-fold (6mm) symmetry of the crystal.
Taken altogether, these results provide compelling evidence that the surface states are localized to individual trilayers as shown in our wavefunction calculations. In Supplementary Note 10, we explicitly show that inter-layer delocalization would lead to the vanishing of γ2 and its associated effects on the band dispersion and spin polarization, thus manifesting the global six-fold symmetry. This also applies to the dispersive bulk states, which should therefore exhibit Rashba interactions with γ2 = 0. It is important to note the critical role played by BiTeCl’s unique symmetry in arriving at this conclusion: in BiTeI and BiTeBr, the entire crystal has the same threefold symmetry as the individual trilayers, so the γ2 term could be non-zero independent of the degree of localization of the wavefunctions.
We now discuss more broadly the significance of higher-order Rashba effects which have been recognized in various contexts for some time21,33; for example, in many semiconductor quantum wells the dominant term is cubic34. More recently, cubic spin–orbit terms were invoked to describe the warping of topological and Rashba surface states22,35,36. Both ARPES and spin-resolved ARPES have been instrumental in revealing these interactions and disentangling them from Dresselhaus-like effects37, anisotropic (non-spin-dependent) band structure38, and magnetic interactions39,40,41. Our experimental observation of the cubic Rashba effect in BiTeCl exemplifies the importance of high-efficiency spin-resolved ARPES measurements, since the spin-reversal occurs in a narrow region of energy-momentum space near EF. We stress the critical role of spin-resolution here, since the reversal occurs where the bands are linearly dispersing, i.e., with otherwise no indication of an anomaly in the spin-integrated data.
Our finding also points to consequences for spintronic applications. Since the reversal occurs in the vicinity of EF, it may provide a mechanism for tuning the polarization of carriers, such as by gating; a similar mechanism has been invoked to explain an unexpected sign change in the spin-polarization of charge carriers injected from quantum point contacts of semiconductor hole gases42. Moreover, the out-of-plane spin component could enable field-free spin–orbit torque switching of perpendicular magnetization43,44. Furthermore, it has been shown that cubic interactions may impact transport properties such as the intrinsic spin-Hall effect45, anomalous Hall and Nerst effects46, magnetotransport47, and thermoelectric transport48. Though additional bands exist near EF in BiTeCl, their contributions may be minimized by surface doping or interface engineering49; crucially, the localized nature of the surface states implies that their binding energies should be tunable by modifying the surface band-bending. Therefore, BiTeCl offers a textbook example of higher-order spin–orbit effects, and can serve as a useful platform for continued exploration of the associated spin-dependent phenomena.
Methods
ARPES measurements
Our spin-resolved ARPES setup is based on a spectrometer with high efficiency attributed to its combination of exchange scattering for spin discrimination and time-of-flight analysis for resolving energy50,51. Band-mapping is performed by rotating the crystal θ (see Fig. 2a), with Γ-K and Γ-M trajectories selected by azimuthal rotation of the sample about its normal. The spin detector can measure the horizontal/vertical spin components (in the lab frame) by rotation of the magnetic scattering crystal, corresponding to Sy/Sz when measuring along Γ-K and Sx/Sz when measuring along Γ-M. The fifth-harmonic of a fiber laser system generates the 6 eV photons for photoemission52. Further experimental details, including our setups for the spin-resolved and spin-integrated ARPES measurements, are described in the Supplementary Notes 1–5.
Sample synthesis and preparation
BiTeCl single crystals were fabricated by the two-step self-flux method. The mixture was slowly cooled from 440 °C to 200 °C in 90 h and annealed at 200 °C for 24 h. The crystals were cleaved under ultrahigh vacuum conditions (<10−10 Torr) and measured at a temperature of 79 K.
Theoretical calculation
Band structure calculations were performed by first considering bulk BiTeCl without spin–orbit coupling using density functional theory with the PBE exchange-correlation functional53, as implemented in Quantum Espresso54. A corresponding tight-binding model is then calculated using Wannier9055, with atomic spin–orbit couplings explicitly added. A 20 trilayer slab is constructed with a band-bending potential shift (see Supplementary Note 6).
Data availability
The ARPES data that support the findings of this study are available at https://doi.org/10.25740/cb936xf9075, and additional data are available upon reasonable request to the corresponding author.
References
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Haldane, F. D. M. Nobel lecture: Topological quantum matter. Rev. Mod. Phys. 89, 040502 (2017).
Wolf, S. A. et al. Spintronics: A spin-based electronics vision for the future. Science 294, 1488–1495 (2001).
Žutić, I., Fabian, J. & Sarma, S. D. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Han, W., Otani, Y. & Maekawa, S. Quantum materials for spin and charge conversion. npj Quantum Mater. 3, 27 (2018).
Bychkov, Y. A. & Rashba, E. I. Properties of a 2D electron gas with lifted spectral degeneracy. JETP Lett. 39, 78 (1984).
Ishizaka, K. et al. Giant Rashba-type spin splitting in bulk BiTeI. Nat. Mater. 10, 521–526 (2011).
Bahramy, M. S., Arita, R. & Nagaosa, N. Origin of giant bulk Rashba splitting: Application to BiTeI. Phys. Rev. B 84, 041202 (2011).
Eremeev, S. V., Nechaev, I. A., Koroteev, Y. M., Echenique, P. M. & Chulkov, E. V. Ideal two-dimensional electron systems with a giant Rashba-type spin splitting in real materials: Surfaces of bismuth tellurohalides. Phys. Rev. Lett. 108, 246802 (2012).
Bahramy, M. S. & Ogawa, N. Bulk Rashba semiconductors and related quantum phenomena. Adv. Mater. 29, 1605911 (2017).
Crepaldi, A. et al. Giant ambipolar Rashba effect in the semiconductor BiTeI. Phys. Rev. Lett. 109, 096803 (2012).
Landolt, G. et al. Bulk and surface Rashba splitting in single termination BiTeCl. N. J. Phys. 15, 085022 (2013).
Sakano, M. et al. Strongly spin-orbit coupled two-dimensional electron gas emerging near the surface of polar semiconductors. Phys. Rev. Lett. 110, 107204 (2013).
Moreschini, L. et al. Bulk and surface band structure of the new family of semiconductors BiTeX (X=I, Br, Cl). J. Electron Spectrosc. Relat. Phenom. 201, 115–120 (2015).
Landolt, G. et al. Disentanglement of surface and bulk Rashba spin splittings in noncentrosymmetric BiTeI. Phys. Rev. Lett. 109, 116403 (2012).
Landolt, G. et al. Direct measurement of the bulk spin structure of noncentrosymmetric BiTeCl. Phys. Rev. B 91, 081201 (2015).
Maaß, H. et al. Spin-texture inversion in the giant Rashba semiconductor BiTeI. Nat. Commun. 7, 11621 (2016).
Shikin, A. M. et al. Anomalously large gap and induced out-of-plane spin polarization in magnetically doped 2D Rashba system: V-doped BiTeI. 2D Mater. 4, 025055 (2017).
Shevelkov, A., Dikarev, E., Shpanchenko, R. & Popovkin, B. Crystal structures of bismuth tellurohalides BiTeX (X = Cl, Br, I) from x-ray powder diffraction data. J. Solid State Chem. 114, 379–384 (1995).
Vajna, S. et al. Higher-order contributions to the Rashba-Bychkov effect with application to the Bi/Ag(111) surface alloy. Phys. Rev. B 85, 075404 (2012).
Fu, L. Hexagonal warping effects in the surface states of the topological insulator Bi2Te3. Phys. Rev. Lett. 103, 266801 (2009).
Cao, Y. et al. Mapping the orbital wavefunction of the surface states in three-dimensional topological insulators. Nat. Phys. 9, 499–504 (2013).
Zhang, H., Liu, C.-X. & Zhang, S.-C. Spin-orbital texture in topological insulators. Phys. Rev. Lett. 111, 066801 (2013).
Jozwiak, C. et al. Photoelectron spin-flipping and texture manipulation in a topological insulator. Nat. Phys. 9, 293–298 (2013).
Sánchez-Barriga, J. et al. Photoemission of Bi2Se3 with circularly polarized light: Probe of spin polarization or means for spin manipulation? Phys. Rev. X 4, 011046 (2014).
Xie, Z. et al. Orbital-selective spin texture and its manipulation in a topological insulator. Nat. Commun. 5, 3382 (2014).
Zhu, Z.-H. et al. Photoelectron spin-polarization control in the topological insulator Bi2Se3. Phys. Rev. Lett. 112, 076802 (2014).
Lin, C.-Y. et al. Orbital-dependent spin textures in Bi2Se3 quantum well states. Phys. Rev. B 98, 075149 (2018).
Jozwiak, C. et al. Widespread spin polarization effects in photoemission from topological insulators. Phys. Rev. B 84, 165113 (2011).
Bawden, L. et al. Hierarchical spin-orbital polarization of a giant Rashba system. Sci. Adv. 1, e1500495 (2015).
Bentmann, H. et al. Profiling spin and orbital texture of a topological insulator in full momentum space. Phys. Rev. B 103, L161107 (2021).
Bihlmayer, G., Noël, P., Vyalikh, D. V., Chulkov, E. V. & Manchon, A. Rashba-like physics in condensed matter. Nat. Rev. Phys. 4, 642–659 (2022).
Winkler, R. Rashba spin splitting in two-dimensional electron and hole systems. Phys. Rev. B 62, 4245–4248 (2000).
Alpichshev, Z. et al. STM imaging of electronic waves on the surface of Bi2Te3: Topologically protected surface states and hexagonal warping effects. Phys. Rev. Lett. 104, 016401 (2010).
Chen, G.-Y. et al. Orbital-enhanced warping effect in px,py-derived Rashba spin splitting of monatomic bismuth surface alloy. npj Quantum Mater. 5, 89 (2020).
Höpfner, P. et al. Three-dimensional spin rotations at the Fermi surface of a strongly spin-orbit coupled surface system. Phys. Rev. Lett. 108, 186801 (2012).
Michiardi, M. et al. Strongly anisotropic spin-orbit splitting in a two-dimensional electron gas. Phys. Rev. B 91, 035445 (2015).
Usachov, D. et al. Cubic Rashba effect in the surface spin structure of rare-earth ternary materials. Phys. Rev. Lett. 124, 237202 (2020).
Schulz, S. et al. Emerging 2D-ferromagnetism and strong spin-orbit coupling at the surface of valence-fluctuating EuIr2Si2. npj Quantum Mater. 4, 26 (2019).
Schulz, S. et al. Classical and cubic Rashba effect in the presence of in-plane 4f magnetism at the iridium silicide surface of the antiferromagnet GdIr2Si2. Phys. Rev. B 103, 035123 (2021).
Chesi, S., Giuliani, G. F., Rokhinson, L. P., Pfeiffer, L. N. & West, K. W. Anomalous spin-resolved point-contact transmission of holes due to cubic Rashba spin-orbit coupling. Phys. Rev. Lett. 106, 236601 (2011).
MacNeill, D. et al. Control of spin-orbit torques through crystal symmetry in WTe2/ferromagnet bilayers. Nat. Phys. 13, 300–305 (2017).
Baek, S. C. et al. Spin currents and spin-orbit torques in ferromagnetic trilayers. Nat. Mater. 17, 509–513 (2018).
Nomura, K., Sinova, J., Sinitsyn, N. A. & MacDonald, A. H. Dependence of the intrinsic spin-Hall effect on spin-orbit interaction character. Phys. Rev. B 72, 165316 (2005).
Krzyżewska, A., Dyrdał, A., Barnaś, J. & Berakdar, J. Anomalous Hall and Nernst effects in 2D systems: Role of cubic Rashba spin-orbit coupling. Phys. Status Solidi - Rapid Res. Lett. 12, 1800232 (2018).
Kim, Y., Lutchyn, R. M. & Nayak, C. Origin and transport signatures of spin-orbit interactions in one- and two-dimensional SrTiO3-based heterostructures. Phys. Rev. B 87, 245121 (2013).
Mawrie, A., Verma, S. & Ghosh, T. K. Electrical and thermoelectric transport properties of two-dimensional fermionic systems with k-cubic spin-orbit coupling. J. Phys. Condens. Matter 29, 465303 (2017).
Men’shov, V. N., Tugushev, V. V., Eremeev, S. V., Echenique, P. M. & Chulkov, E. V. Band bending driven evolution of the bound electron states at the interface between a three-dimensional topological insulator and a three-dimensional normal insulator. Phys. Rev. B 91, 075307 (2015).
Jozwiak, C. et al. A high-efficiency spin-resolved photoemission spectrometer combining time-of-flight spectroscopy with exchange-scattering polarimetry. Rev. Sci. Instrum. 81, 053904 (2010).
Gotlieb, K., Hussain, Z., Bostwick, A., Lanzara, A. & Jozwiak, C. Rapid high-resolution spin- and angle-resolved photoemission spectroscopy with pulsed laser source and time-of-flight spectrometer. Rev. Sci. Instrum. 84, 093904 (2013).
Ishida, Y. et al. High repetition pump-and-probe photoemission spectroscopy based on a compact fiber laser system. Rev. Sci. Instrum. 87, 123902 (2016).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Mostofi, A. A. et al. An updated version of wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 185, 2309–2310 (2014).
Acknowledgements
We are grateful for helpful technical discussions with C. Jozwiak. This work was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Science and Engineering. Early instrument development of the spin-resolved ARPES setup was partially funded by the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF4546 to ZXS. Part of the numerical calculations were performed using the resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility operated under Contract No. DE-AC02-05CH11231. S.S. acknowledges financial support from the JSPS Research Fellowship for Research Abroad. H.L. acknowledges support from the National Natural Science Foundation of China (N0.11904236).
Author information
Authors and Affiliations
Contributions
J.Q. and J.A.S. prepared the manuscript with input from all co-authors. J.Q., X.H., S.S. and J.A.S. performed the experiment. C.J., M.S., B.M. and T.P.D. performed theoretical calculations. J.L., H.L., D.G. and Y.-J.Z. grew single-crystal samples. P.S.K., Z.H., Z.-X.S., and J.A.S. provided oversight and infrastructure support.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qu, J., Han, X., Sakamoto, S. et al. Reversal of spin-polarization near the Fermi level of the Rashba semiconductor BiTeCl. npj Quantum Mater. 8, 13 (2023). https://doi.org/10.1038/s41535-023-00546-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-023-00546-x