Introduction

Planar Hall effect (PHE) is a unique transport phenomena driven by an in-plane magnetic-field-induced rotation of the principal axes of the resistivity tensor1,2. Because of different origins, the PHE is in many aspects quite different from those Hall effects driven by an out-of-plane magnetic field or magnetization as shown in Fig. 1a. Obvious PHE has been observed in a few ferromagnetic metals1,2 and nonmagnetic semimetals with strong orbital anisotropy of electronic structure3,4. It is widely used for designing and fabricating commercial magnetic sensors, especially for three-dimensional (3D) highly compacted, and ultra-sensitive ’lab-on-a-chip (LOC)’ devices for the next generation chips. Another great interest for PHE lies in its angular dependence of the direction of magnetic field, which can be applied to infer the information of the underlying magnetic order or electronic structure. For example, to investigate this effect and pursue its origin in a quantum system may reveal nontrivial topological physics or reveal the exotic states and orders to advance the understanding of fundamental physics5,6,7,8,9,10.

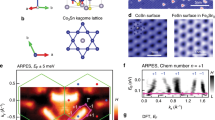
Fig. 1: Schematics and typical results of the measurements for PHE and PAMR.
figure 1

a Schematic of the geometry of the device in our measurements for the ordinary Hall, planar Hall, and longitudinal resistivity. Inset: the picture of our device. b Crystal structure of KV3Sb5. θ is defined as the angle between the directions of current and in-plane applied field. For our device, the current is along a axis. c The PHE in Co3Sn2S2, ZrSiSe, and TaSe332,33,34,35,36,37. The insets: the crystal structure and Fermi surface in these three materials. d, e ρxy(θ) and ρxx(θ) with μ0H = 2 T at 10 K marked by blue open squares. The black solid lines indicate the ρxy(θ) and ρxx(θ) for conventional PHE and PAMR described by formula 1 and 2 respectively, which are also plotted in the insets exhibiting two-fold symmetry by the color contours in polar coordinates where the r axes are ρxy(θ) and ρxx(θ) respectively, and θ is the rotating angle defined in (a).

Full size image

Recently, superconductivity was observed in a new family of layered kagome metals AV3Sb5 (A = K, Rb, Cs)11,12,13,14,15,16. Their normal states are identified as Z2 topological metals with multiple topologically nontrivial band structures such as flat band, van Hove singularity, and Dirac-fermion dispersion in close proximity to the Fermi level17,18,19,20,21,22. In the absence of magnetism, it is surprising to observe a giant anomalous Hall effect (AHE) in these materials. To reconcile the observations, the AHE is considered to strongly correlate to novel orders such as chiral charge-density-wave (CDW) or nematic order accompanying with symmetry breaking23,24,25,26,27,28,29,30,31. However, because the correlations among spin, charge, lattice, and other orders are expected to be important, it remains a great challenge to get a full understanding of the origin of the various novel transport properties observed in this family of materials. In this work, we observe prominent PHE and planar anisotropic magnetoresistivity (PAMR) in KV3Sb5. More interestingly, below the CDW transition the in-plane applied magnetic field drives exotic higher-order oscillations for PHE and PAMR violating the empirical law in former materials (even in recent topological materials). The unique behaviors exhibit strong field response accompanying with non-monotonous anisotropic field dependent in-plane resistivity. These abnormal planar transport properties suggest a strong coupling between transport electrons and anionotropies from the system with various orders in contrast to other materials. By scrutinizing various possible mechanisms, we suggest a significant interplay of the lattice, magnetism, and electron associated with the fluctuations as the media leading to those unconventional transport behavior.

Results

Conventional planar Hall effect PHE and PAMR

As shown in Fig. 1a, the PHE and PAMR can be characterized by measuring the transverse resistivity (ρxy) and longitudinal resistivity (ρxx) with applying an in-plane magnetic field (rotating within the ab plane of KV3Sb5 shown in Fig. 1b) which fails to drive the ordinary Hall effect (OHE) measured with an out-of-plane magnetic field. Usually, obvious PHE and PAMR are only observed in a few kinds of materials and follow the angular dependence as:

$${\rho }_{xy}=-\Delta \rho \sin \theta \cos \theta ,$$
(1)
$${\rho }_{xx}={\rho }_{\perp }-\Delta \rho \,{\cos }^{2}\theta ,$$
(2)

where ρxy represents the in-plane Hall resistivity that directly shows the PHE, ρxx is the PAMR, and Δρ = ρ⊥ − ρ∥ is the resistivity anisotropy (called chiral resistivity in topological materials) with ρ⊥ and ρ∥ representing the resistivity with the applied field μ0H perpendicular (90∘) and parallel (0∘) to the electric current respectively1. According to these formulas, angular dependent ρxy (ρxy(θ)) and ρxx (ρxx(θ)) exhibit twofold oscillations and a relative 45∘-angle shift for ρxy(θ) and ρxx(θ) as shown in Fig. 1d, e32,33,34,35,36,37. It is observed the anisotropy from lattice, magnetism, or Fermi surface, etc usually hardly affect the in-plane transport behavior such as PHE and PAMR. For KV3Sb5, obvious PHE and PAMR are observed at 2 K even with a small applied field of μ0H = 2 T after subtracting the OHE and out-of-plane magneto resistivity9,13. ρxy and ρxx (shown in Fig. 1d, e) exhibit two-fold symmetrical oscillations and roughly follow the conventional angular dependence. The little discrepancy between our results and empirical formulas can be attributed to the existence of additional higher-order oscillations (discussed below).

Higher-order oscillatory planar Hall effect

With increasing the applied field (μ0H), as shown in Fig. 2, at 2 K additional features are observed in ρxy at 90∘ and 270∘ with μ0H = 7 T accompanying with the emergence of additional small peaks in ρxx(θ) at 0∘ and 180∘. With further increasing μ0H to 14 T, the oscillations of both ρxy(θ) and ρxx(θ) exhibit prominent higher-order oscillatory components in sharp contrast to those for conventional PHE and PAMR with only two-fold symmetrical oscillations. To investigate these phenomenons, Fast Fourier transform (FFT) is applied for ρxy(θ) and ρxx(θ) at 2 K with various applied fields as shown in Fig. 3a, b. Besides the peaks at 180∘ in FFT spectrum relating to two-fold symmetrical oscillations, another obvious peaks at 90∘ are observed at high fields whose amplitude is larger than those at 180∘, indicating the appearance of four-fold symmetrical oscillations. With decreasing μ0H, these four-fold symmetrical oscillations become weaker and their amplitudes shrink to the value smaller than those with two-fold symmetry at μ0H = 5 T shown in Fig. 3c, d. With decreasing μ0H to 2 T, the FFT peaks at 90∘ are much weaker than those at 180∘, indicating the oscillations mainly containing two-fold symmetry component. In addition, small peaks are observed at 60∘ in the FFT spectrum for ρxx(θ), suggesting the appearance of six-fold symmetrical oscillation which are much weaker than the two-fold and four-fold symmetrical oscillations. To gain more clues on the emergence of higher-order oscillatory components, the field dependent Hall and longitudinal resistivity ρxy(H) and ρxx(H) are measured with rotating an in-plane applied field at angles from 0∘ to 90∘ shown in Fig. 3e, f. In these color contour plots, it is clearly observed that minimums appear around 45∘ and 20∘ for ρxy(H) and ρxx(H) at high fields, respectively, which is consistent with the emergence of additional higher-order oscillatory components (especially the four-fold symmetrical oscillatory components) in our former results and analysis for ρxy(θ) and ρxx(θ).

Fig. 2: PHE and PAMR for KV3Sb5 at 2 K.
figure 2

a, c The 2D color plots for PHE and PAMR at 2 K with μ0H = 2, 7, 10, and 14 T respectively in the polar coordinates where r represents the applied field, θ is the rotating angle, the red region represents higher resistivity, and the blue region represents lower resistivity. b, d The related data of ρxy(θ) and ρxx(θ) from (a, c). The experimental data are marked by open symbols and the fitting curves by formulas 3 and 4 marked by solid lines.

Full size image
Fig. 3: The analysis of symmetry for oscillatory PHE and PAMR.
figure 3

a, b The Fast Fourier Transform (FFT) spectrum of ρxy(θ) and ρxx(θ) at 2 K with μ0H = 2, 3, 4, 5, 7, 10, and 14 T. c, d The field dependence of high-order oscillatory coefficients for PHE and PAMR. S2, S4, S6, C2, C4, and C6 are acquired from the amplitude of peaks of FFT spectrum of (a, b). Sxy2, Sxy4, Cxx2, Cxx4, and Cxx6 are acquired from the data fitting for the formulas (3) and (4). e, f The color plots for field dependent planar Hall and longitudinal resistivity ρxy(μ0H) and ρxx(μ0H) at the angles from 0∘ to 90∘ with the step of 10∘.

Full size image

Figure 4a, b present the temperature dependence of ρxy(θ) and ρxx(θ) with μ0H = 14 T, respectively. By the similar FFT analysis shown in Fig. 4c, d, it is observed that the high-order oscillatory components relating to the four-fold symmetrical oscillation appear below the CDW transition (identified by an anomaly in temperature-dependent resistivity along c axis around 80 K here), and increase obviously with decreasing the temperature, as shown in Fig. 4e. Above 80 K, the oscillations of ρxy(θ) and ρxx(θ) only contain two-fold symmetrical oscillatory component and can be well described by empirical formulas 1 and 2. To pursue the origin of the observed unconventional PHE and PAMR, we first carefully check the extrinsic contributions, such as current jetting effect due to the inhomogeneous current distribution38. The possible tiny current distortion in our devices is difficult to drive additional prominent oscillations here (see Supplemental Fig. 2). The intrinsic origins usullay can be (1) the spin-dependent scattering due to the classical orbital magnetism or the interactions of the magnetic order and the spin-orbit coupling38, (2) chiral anomaly in a nonmagnetic topological system5, and (3) anisotropically lifting the protection of surface Dirac fermions from backscattering in a topological insulator10. However, these mechanisms can only host to the two-fold symmetrical oscillations for PHE and PAMR obeying the conventional formulas (1) and (2) and fail to result in high-order oscillatory components.

Fig. 4: The phase diagram for evolved high-order components of PHE and PAMR.
figure 4

a, b The typical ρxy(θ) and ρxx(θ) with μ0H = 14 T at 2, 40, and 80 K. The fitting curves are marked by black solid lines. c, d The FFT spectrum of ρxy(θ) and ρxx(θ) with μ0H = 14 T at 2, 10, 20, 40, 60, 80, and 100 K, respectively. e The temperature dependent anomalous Hall resistivity \({\rho }_{xy}^{\rm{AHE}}\) for two samples are shown with the left axis. The data of black line are acquired from our measurements and the data of blue line are acquired from ref. 27. The temperature dependent Sxy4 and Cxx4 for ρxy are also shown with the left axis. The temperature dependent resistance along c axis R\({}_{xx}^{c}\) is shown with the right axis with a prominent CDW anomaly around 78 K . f The schematic for the coupling between distorted lattice and Fermi surface leading to high symmetrical oscillatory PHE driven by an in-plane field.

Full size image

Discussion

Usually the additional anisotropy from a system is difficult to behave in conventional PHE and PAMR even the system hosts high anisotropic Fermi surface, magnetism, or lattice such as in kagome magnet Co3Sn2S2, tetragonal ZrSiSe, and quasi-one dimensional TaSe332,33,34,35,36,37. However, these additional anisotropies should be considered in KV3Sb5. The anisotropic Fermi surfaces (triangular-shaped pockets) are observed around M point27, but the shape of the Fermi surface changes little in the presence of CDW order and higher-orders oscillatory PHE and PAMR, which is unlikely to bring the appearance of large anisotropy in carrier density and scattering rate directly. Thus the mechanism applied to explain the higher-order oscillations in materials such as bismuth or (111) LaAlO3/SrTiO3 oxide interface4,39,40 is not applicable. In KV3Sb5 no long-range or short-range magnetic orders were observed, thus the anisotropy from conventional static magnetic order also seems not applicable. In semi-class model, the resistivity comes from the electron scattering with the lattice. Thus the anisotropy of the lattice can naturally host anisotropic carrier scattering with constrictions of the lattice’s symmetry. It is noticed that even in presence of some distortion due to the CDW the lattice for KV3Sb5 still keeps hexagonal structure. In the two dimensional case with C6 rotation invariance39, ρxy(θ) and ρxx(θ) can be expressed as:

$${\rho }_{xy}={S}_{xy2}\sin (2\theta -2\phi )+{S}_{xy4}\sin (4\theta +2\phi ),$$
(3)
$${\rho }_{xx}={C}_{xx0}+{C}_{xx2}\cos (2\theta -2\phi )+{C}_{xx4}\cos (4\theta +2\phi )+\,{C}_{xx6}\cos 6\theta ,$$
(4)

where Sxy2, Cxx2, Sxy4, Cxx4, and Cxx6, are the coefficients for two, four, and six -fold symmetrical oscillations for PHE and PAMR related to lattice symmetry39 (see Supplementary Note 4). ϕ is the angle between the current I and a axis and here ϕ = 0 with I // a. By using these formulas, the our data can be well fitted in consisted with former FFT analysis. Above CDW transition Sxy4, Cxx4, and Cxx6 become to zero, the formula 3 and 4 become to formula 1 and 2 respectively indicating the PHE and PAMR obeying the conventional empirical law. Below the CDW transition, Sxy4, Cxx4, and Cxx6 increase with the decreasing temperature and exhibit a strong field response with more contributions for oscillatory ρxy and ρxx at high fields. The temperature and field dependence of high-order oscillatory components (Sxy4, Cxx4, and Cxx6) suggests the strong enhancement of a unique coupling between anisotropy from lattice and electrons scattering for planar transport behavior. Besides, recently, we also noticed the observation for possible domains for three nematic orders, which may also bring the additional anisotropies for the abnormal PHE and PAMR41.

Accompanying with CDW transition, it is observed that obvious multiple fluctuations emerge simultaneously. From lattice side, strong phononic fluctuations were revealed accompanying with lattice distortions42. From the electronic side, the electronic instability can host electronic fluctuations (including the nematic fluctuations) and result in electronic nematicity at lower temperatures with symmetry reduction43. Moreover, from magnetism side, for KV3Sb5 though in absence of long-range or short range magnetic order, the magnetic fluctuations due to observed orbital ordering would inherit the crystalline anisotropy of the kagome lattice which plays a crucial role in the magnetic properties, especially for the appearance of time-reversal symmetry breaking. We find that the observed ρ∥ < ρ⊥ (see Fig. 2) is consistent with this picture since a magnetic field will suppress magnetic fluctuations in the field direction. In fact, these fluctuations are correlated and can origin from same instability due to CDW transition indicating presentence of multiple orders in the system. These correlated fluctuations can be attributed to mediate the crystalline anisotropy and electron scatterings for planar resistivity tensors to behave higher-order oscillatory components (as shown in Fig. 4f) revealing a unique interplay of lattice, electron and magnetism in KV3Sb5.

In summary, prominent PHE and PAMR are observed in KV3Sb5. The applied field would drive higher-order oscillations for both ρxy and ρxx below the CDW transition, resulting in the violation of the empirical law. This exotic phenomena suggests a strong and complicated coupling between lattice symmetry and electron scatterings for planar transport properties. We expect that such unconventional PHE and PAMR are not only potential for next generation 3D chips, but also reveal a unique interplay between various degrees of freedom for materials with frustrated crystal structures, lattice distortions and anisotropic magnetic fluctuations.

Methods

Single crystals preparation

Single crystals of KV3Sb5 were grown via the self-flux method. K, V and Sb were mixed by the ratio of 1:1:4.5 and sealed inside a Ta crucible. This Ta crucible was subsequently inside in evacuated quartz tube. The mixture was heated to 1000 °C, slowly cooled to 700 °C, and finally decanted by a centrifuge. Planar single crystals with typical dimensions of 2 × 3 × 0.3 mm3 were harvested at the bottom of the crucible.

Crystal structure characterization

Crystal structure and elemental composition were confirmed by X-ray diffraction (XRD) and energy dispersive spectrometer (EDS). Sharp peaks in the XRD confirm high crystalline quality of the samples.

Device fabrication

The Hall-bar devices were fabricated by exfoliating the single crystal of KV3Sb5 on to a SiO2/Si substrate. Electronic contacts were added via patterned mask with photolithography subsequent growth of Ti/Au(10 nm/100 nm) layers. Electrical transport measurements were performed in a Physical Properties Measurement System (PPMS Dynacool, Quantum design). Direct current (DC) magnetization and alternating current (AC) susceptibility measurements were performed in a Magnetic Property Measuring System (MPMS Quantum design).