Abstract
The presence of inclusions, twinning, and low-angle grain boundaries, demanded to exist by the third law of thermodynamics, drive the behavior of quantum materials. Identification and quantification of these structural complexities often requires destructive techniques. X-ray micro-computed tomography (µCT) uses high-energy X-rays to non-destructively generate 3D representations of a material with micron/nanometer precision, taking advantage of various contrast mechanisms to enable the quantification of the types and number of inhomogeneities. We present case studies of µCT informing materials design of electronic and quantum materials, and the benefits to characterizing inclusions, twinning, and low-angle grain boundaries as well as optimizing crystal growth processes. We discuss recent improvements in µCT instrumentation that enable elemental analysis and orientation to be obtained on crystalline samples. The benefits of µCT as a non-destructive tool to analyze bulk samples should encourage the community to adapt this technology into everyday use for quantum materials discovery.
Similar content being viewed by others
Introduction
Materials behavior is critically impacted by extended structure complexity on the micron/nanometer scale. These hierarchical structures can hinder or enhance the desired properties, especially for quantum materials where a balance of energy scales makes the ground states particularly sensitive1,2,3. While more focus is directed on the atomic scale and periodicities, bulk features (on the scale of >1 µm) can also mask the intrinsic behavior of a sample. To avoid these is impossible according to the third law of thermodynamics, but, to even controllably tune these intricacies is difficult depending on the synthesis conditions, as seen in materials such as metal alloys, crystal scintillators, and thermoelectrics4,5,6,7. This can be troublesome in particular for quantum materials, where inclusions, low-angle grain boundaries, crystal twinning, and other structural imperfections can impact the physical properties of a material, such as in the superconductors YBa2Cu3O7-δ (impacting the critical current density) and Sr2RuO4 (impacting the Tc)8,9,10,11,12.
Many characterization techniques commonly used probe too small-scales, focus solely on the surface, and/or require destruction of the sample to visualize and quantify such features13,14,15. X-ray micro-computed tomography (µCT) is a non-destructive alternative technique that allows one to obtain a 3D representation of the sample with resolution in the µm to nm range. This method uses high-energy X-rays to transmit through the sample, collecting multiple images that are then reconstructed into a 3D object where extended structural features can be visualized through a variety of contrast methods16. Since its conception, µCT has been integrated as a routine characterization tool for a variety of fields, including medicine17, biology18, and geology19. While this method of characterization is used extensively in materials science20, for the condensed-matter community it has only recently been adopted in the analysis of electronic and quantum materials21,22,23. Throughout this paper, we demonstrate examples in which µCT can be an important characterization tool to aid in materials design and show insights that would not be possible without this technique.
Results and discussion
Volumetric measurements and sample porosity
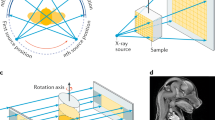
Figure 1a shows a general schematic of the key components of a µCT instrument. In this technique, X-rays transmits through the sample from a polychromatic source, usually following a cone or fan beam geometry. The X-rays then hit the scintillation detector, collecting a series of images while the sample rotates on a platform by 180° or 360° (dependent on sample geometry). From this point the collection of images is used to reconstruct the 3D sample, typically done using a filtered back-projection algorithm. There are a variety of collection/reconstruction strategies and algorithms to avoid artifacts that are better addressed in related reviews19,24. The reconstruction is a 3D representation, with voxel (3D pixel) by voxel contrast measurement (e.g., Beer’s law in the case of X-ray attenuation contrast). This contrast allows for the characterization of a variety of defects that plague electronic and quantum materials, examples of which are shown in Fig. 1b in accordance with the time and length scales they occur. Common inhomogeneities that impact materials’ properties, along with their corresponding dimensionalities, are listed in Table 1, adapted from ref. 25. These are wide ranging in dimensionality and much work has been dedicated to controlling their origin26,27,28,29,30,31,32,33.
a A representation of the key components in a µCT instrument. The X-ray source shown generates X-rays in a cone-beam geometry as they transmit through the sample and hit the scintillation detector, all while the sample rotates on a stage. b A comparison of the various time and length scales defects can form in electronic and quantum materials.
A simple measurement attained from µCT is sample geometry down to ~µm–nm resolution. This is especially helpful for thermal/electrical transport measurements of geometrically complex samples where an accurate volume or cross-sectional area are still needed. It enables the determination of density, as well as the observation of voids or cracks that can impact the transport properties34. Alongside techniques such as resonant ultrasound spectroscopy, it also enables rigid body simulations for determining vibrational response, allowing extraction of phonon properties.
These volumetric measurements can be helpful when one is doing a high throughput search of materials where crystal growth may be too difficult or time-consuming, instead relying on well-compacted powders using instruments such as a spark plasma sintering system35. In this example, being able to calculate the porosity, or % volume of voids in relation to the total volume, would be useful for comparison. Figure 2a shows an example of Cu powder that was cold pressed to better emphasize the size of voids that can occur. As air is less attenuating than the bulk, the voids can be easily visualized and then quantified using µCT. One can quantify the number of detected voids to be 67 and their volume distribution can be visualized in the histogram distribution in Fig. 2b. In this example, most voids are a volume of similar magnitude of each other. While other techniques can be used to quantify pores, µCT gives us a look at the 3D structure, highlighting internal voids that may be more difficult to characterize. This type of measurement expands the characterization methods possible in determining sample quality, bolstering the validity of the results of transport measurements.
Inclusions from flux crystals
The previous example showed an important insight in the application of µCT, that sample components can be distinguished and visualized non-destructively throughout the bulk. This contrast method can occur when the compounds have different attenuation coefficients in the operating X-ray voltage of the instrument. This ability can be put to great use in flux crystal growth. In the flux method, one uses an excess of a compound to dissolve the desired material below its melting point, where upon gradual cooling the flux reaches supersaturation resulting in crystallization of the target sample. This technique is widely used in materials discovery as a low-cost method to grow millimeter-scale crystals36,37.
For both oxides and metals, one would normally use a flux that is chemically related to the target material, but sometimes an unrelated compound must be used. Poor selection of flux would result in a mixture of phases and poor crystallite size, where µCT could be utilized to help understand the growth formation mechanisms and segregation of phases if combined with a secondary technique such as powder X-ray diffraction to understand phase composition. Even use of a successful flux can still result in inclusions in the sample that can impact materials properties, as well as be indistinguishable without destroying the crystal38.
A classic example of this is the material SmB6, a well-known Kondo insulator with reported quantum oscillations that supports the suspected topological behavior39. The most common method to grow this material is by using an excess of Al flux, which can show up as inclusions21. Figure 3a is a graph of the attenuation coefficients of Al and SmB6 as a function of X-ray voltage showing that provided one is in the right range of energy (in this case the operating range of the instrument), it is easy to distinguish these inclusions from the bulk sample. A comparison of the crystal structure between SmB6 and Al in Fig. 3b shows that given the similar structure and lattice parameter, the two materials will likely seed the growth of one another. Figure 3c and d demonstrates this, where flux grown SmB6 crystals with epitaxially grown Al inclusions is visualized using µCT. Measurements of samples while systematically thinning the crystal show a disappearance in the quantum oscillations40. Since the presence of Al makes it difficult to elucidate the inherent characteristic behavior of SmB6, µCT can be combined with other measurements (such as bulk magnetization) as an effective way to non-destructively screen samples.
a A comparison of the attenuation coefficients of Al and SmB6 as a function of X-ray energy in the operating range of the instrument, demonstrating the feasibility of contrasting the two components using µCT. The K-edge for Sm lies at 46.83 keV, resulting in the dip of attenuation. b Visualizations of the crystal structure of SmB6 and Al, demonstrating that given the similar lattice parameter, both systems mutually support the growth of one another. c A 3D rendering of a crystal of SmB6 showing the presence of Al inclusions (colored yellow) that are epitaxially oriented. d A rendering of a different crystal of SmB6 with Al inclusions showing up as epitaxially oriented layered sheets. e A 3D rose diagram generated from the star volume distribution (SVD) of the inclusions of (c). The data are oriented along the length of the crystal, showing a preferred growth direction following the crystal habit. The image is colored according to distance from origin. f A 3D rose diagram generated from the SVD of the inclusions of (d), showing the impact the opposing layers have on the overall anisotropy. The image is colored according to the distance from the origin.
Screening samples is helpful, but in this example µCT also gives us information regarding the formation of these extended features. Not only do we see the presence of inclusions, but we also see that they are not uniformly distributed throughout the sample and instead develop a preferred orientation. The absorption data collected lets us quantify the size, distribution, and orientation of these inclusions using software such as Blob3D and Quant3D41,42.
One measurement that can be performed is the star volume distribution (SVD), with other examples being the mean intercept length and star length distribution. For a distribution of points in the segmented data, the SVD determines the distance traveled before the interception of a boundary, with the measurement performed over the volume of the specimen43. We can use such measurements of the Al to calculate a degree of anisotropy of 0.96 (where a value of 0 is completely isotropic and 1 is completely anisotropic). The ratio of the largest eigenvalue over the smallest is another measure of the degree of anisotropy (DA) and is 220(20) for Fig. 3c. We can then further generate a 3D rose diagram, a projection of the calculated SVD measurements, to visualize the directionality of these features relative to the crystal itself, as seen in Fig. 3e. The diagram shows that the inclusions preferentially grow along the length of the crystal.
As the same material can form different crystal habits, µCT as a tool affords us the opportunity to compare the inclusions between different crystal shapes of SmB6, previously never investigated in the community. The more cuboid-shaped crystals, as rendered in Fig. 3d, show sheets of aluminum form perpendicular to the main crystal axis. The eigenvalue DA determined through Quant3D is. 2.75(9). A visualization of the Al using a 3D rose diagram of the SVD in Fig. 3f shows a different form of anisotropy compared to the SmB6 rods. In this case, two competing sheet-like layers are developed in opposing crystalline directions. The data shows that in the discovery of quantum materials, extended features do matter and techniques such as µCT should be implemented to carefully examine the distribution of such inhomogeneities. Further work can be performed using this method to analyze inclusions of other materials exhibiting quantum oscillations to correlate the orientation with the quantum oscillation frequency44.
While SmB6 serves as a shining example of the power of µCT, this technique can be used beyond detecting defects to also help optimize crystal growth parameters. This is demonstrated in the case of rutile GeO2 (r-GeO2), an ultra-wide band gap semiconductor with predicted ambipolar doping. Much work has been invested in the development of controlled defects in bulk and thin film samples to invoke these aforementioned properties for electronic devices45,46,47. Here, we discuss the improvement in crystal quality of flux grown single crystals of r-GeO2. In flux growths, the cooling rate can have a large impact on not only the size, but also the quality of the crystals obtained. In Fig. 4a, we see a single crystal of r-GeO2 grown using flux method with a cooling rate of 3 °C/h. Laue diffraction shown in Fig. 4b gives clear, defined spots along one of the facets.
a A single crystal of rutile GeO2 grown using a flux with a cooling rate of 3 °C/h. b Laue diffraction image of the crystal along the [011] direction. c A representation of a crystal from the same batch as (a) generated from µCT data with voids present (highlighted blue). d A 3D rose diagram of the star volume distribution of the voids. The data was aligned such that the void shows a preferential orientation parallel to the [011] direction of the crystal axis. The image is colored according to the distance from the origin. e A different crystal of rutile GeO2 grown using a flux with a cooling rate of 0.5 °C/h. f A rendering of a crystal from the same batch as (e) showing no detectable voids.
Further inspection using X-ray µCT in Fig. 4c shows voids present in the sample. We calculate the degree of anisotropy to be 0.79, with a 3D rose diagram generated in Fig. 4d. The eigenvalue DA determined through Quant3D is 7.6(7). In this instance, the axes were aligned to the [011] direction, showing a preferred orientation of the voids parallel to the crystal facet. A similar crystal of r-GeO2 cooled at a rate of 0.5° C/h through the same temperature range shows no sign of voids above the µm scale. The improved quality of this crystal is seen in the optical microscope image of Fig. 4e, and the volumetric rendering shown in Fig. 4f. This example follows the common logic that a slower growth leads to better quality crystals, although this need not always be the case. Through this comparison, we show how µCT can be implemented in flux crystal growth to screen crystals for inclusions as well as help optimize the growth parameters. We also see that dependent on the crystal habits, one can quantify features accurately along crystallographic orientations.
Extended defects in floating zone samples
Flux growth has been the primary form of synthesis discussed so far, but X-ray µCT can assist other synthesis approaches and crystal growth methods. Techniques involving directional solidification, such as Bridgman and floating zone, can also be affected by inclusions as well as voids and air pockets that incorporate into the grown crystal48,49,50. These defects impact crystal quality but can be prevented by improvements in sample preparation or changes in the growth parameters. An example of this can be considered in the floating zone technique. Internal voids can form in this technique due to air pockets in poorly densified rods as well as the generation of gas as a side product when the compound melts51. A less obvious method of void formation is due to the gas environment itself. While applied pressure of different gas species can be useful in floating zone growths to reduce volatility or stabilize certain oxidation states, it can be detrimental to growth stability as well52,53.
We demonstrate the applicability of µCT in analyzing these internal voids in the floating zone growth of YbMgGaO4. This material, whose crystal structure is shown in Fig. 5a, is a quantum spin liquid candidate due to the frustrated triangular lattice Yb3+ ions occupy54,55. µCT data collected on a section of a sample grown in PARADIM’s 300 bar optical high-pressure floating zone is visualized in Fig. 5b to highlight the presence of internal voids. In this case, a larger applied pressure of 20 bar of O2 gas led to void formation compared to an applied pressure of 5 bar done in previous papers, likely due to the dissolution of the gas at higher pressures.
a The crystal structure of YbMgGaO4 showing its trigonal nature. b A rendering of the melt from a high-pressure floating zone growth of YbMgGaO4 characterized by µCT to highlight the presence of internal voids, colored to be visually distinct from one another. c An optical microscope image of the melt from the growth, showing the presence of external voids detectable by the eye. d A contour map of the melt’s void volume as a function of their relative orientation. Weak anisotropy is present as the samples grow larger in volume. Distances between the largest size voids are emphasized to show the directionality obeying the trigonal structure.
Figure 5c shows an optical microscope image of the melt as support for both the presence of detectable voids as well as their directionality. To further understand the anisotropic nature of these features, the relative orientations of the voids according to their volume are shown using a contour plot in Fig. 5d. The larger voids tend to cluster around certain areas of orientation, showing a weak anisotropy present as a function of volume, supported by the calculated degree of anisotropy being 0.39. This intuitively makes sense, as the larger size pockets are present in the growth for a longer time and hence have more directionality applied to them because of the growth method itself. Examining the distance between the largest pockets show angles of ~30° and ~120°, supporting the proposed trigonal structure of the material.
Recent developments in instrumentation
All experiments shown so far were accomplished using a typical lab-bench-sized µCT instrument, showcasing the power of this technique in an accessible research environment. Further advances in instrumentation open up possibilities in using µCT to inform materials synthesis. The onset of accessible hyperspectral detectors has given µCT the ability to perform 3D bulk elemental analysis on the scale of µm56. This capability could easily be applied to materials synthesis involving complex phase diagrams. In these cases, distinguishing between the different components may not be naively easy without the use of hyperspectral detectors.
Where the hyperspectral detector allows for elemental analysis, Diffraction µ-Computed Tomography (DCT) allows for orientation analysis of 3D volumes of both polycrystalline and single crystalline samples57. This has already had some use in ceramics to track grain growth while sintering and has been shown to inform crystal morphology in materials discovery58,59. Being able to follow grain selection in floating zone growths using DCT could be used alongside current methods to allow for a better optimization of growth conditions60.
An example of such visualization is shown in Fig. 6a, where we have performed DCT on a floating zone-grown crystal of rutile TiO2. Since rutile and other similar materials are desired for their large birefringence, low-angle grain boundaries can be harmful to their optical properties61,62. The grains are clearly highlighted in the diffraction data, as this was a piece from early in the growth where multiple domains are still competing. An interesting observation in the absorption data is shown in Fig. 6b, where a Sobel filter was applied to emphasize edges. Without any knowledge of the diffraction data, one can still visualize some grains due to inherent gaps created between the domains. This can lead to normal µCT being a useful screener prior to DCT in identifying potential boundaries present. We can use the combined data to determine domains for sample extraction, as well as to understand more about growth mechanisms occurring, in particular for cases where competing polytypes and intergrowths could be occurring63,64.
Techniques such as in situ XRD available at synchrotron facilities already allow for insights into sample synthesis routes65,66. Current µCT instruments allow for the application of heating, cooling, and force to examine changes over time. Applying in situ µCT in a crystal growth process would take us one step further and allow one to have a pseudo-real-time response to conditions to avoid defects and inclusions. A traditional floating zone setup that incorporates translating/rotating samples could be adapted for such a purpose, where once steady state has been achieved, a crystal growth is occurring at a (normal) slow rate and rotating for each collection of images. While data sets of µCT are normally gigabytes to terabytes in size, to process and describe this amount of data is an example of “big” data challenges the community needs to address in the future of guided materials discovery.
Throughout this review, we have shown the capabilities of µCT in aiding materials design. The data collected through this technique can aid other characterization methods through the calculation of volumes and quantification of pore sizes for transport measurements. The detection of inclusions can help non-destructively screen samples for quality as well as give insight into defect formation/orientation. Sample synthesis can be improved upon through the analysis of extended features, such as voids that are sometimes hidden in other techniques. Finally, we showed how advances in µCT instrumentation can expand upon the current capabilities by allowing for elemental and orientation analysis as well as in situ measurements. Overall µCT is an effective non-destructive characterization tool that can be widely implemented throughout the materials community to assist in the synthesis of electronic and quantum materials.
Methods
Crystals of SmB6 were grown following a similar procedure of Phelan et al.21. Crystals of r-GeO2 were grown following a similar procedure of Niedermeier et al.46,67. Initial powder and floating zone rods of YbMgGaO4 were prepared following a similar procedure to Li et al.54. Crystals were grown using the 300 bar high-pressure floating zone furnace (SciDre GmbH) at the Platform for the Accelerated Realization, Analysis and Discovery of Interface Materials (PARADIM) user facility at Johns Hopkins University. A 5 kW Xenon arc lamp was utilized as a heating source at a pressure of 20 bar with an oxygen flow rate of 0.1 L/min. Feed and seed rods were rotated together at 20 rpm. The feed rod and the seed rod were advanced at rates of 10 to 12 mm/h and 10 mm/h, respectively. Crystals of r-TiO2 were grown following the procedure of Wright et al. with no sample rotation applied for either the seed or feed rod60.
Standard µCT data were collected using a Bruker SkyScan 1172 with an operating range of 20–100 kV for the X-ray source and 0.9 µm maximum pixel resolution using an Al+Cu filter. Specifically, the point-spread function for each measurement is listed in Table 2 following the procedure of Ketcham et al.68. Reconstructions were done using NRecon with ring artifact removal and beam hardening correction algorithms applied. The reconstructed data were visualized and analyzed using Dragonfly software, Version 2021.1 for Windows (Object Research Systems (ORS) Inc, Montreal, Canada, 2020; software available at http://www.theobjects.com/dragonfly). Measurements used for the 3D rose diagrams were generated using Quant3D (https://www.ctlab.geo.utexas.edu/software/quant3d/). Diffraction computed tomography data were collected using a Zeiss Versa 620 with a voxel size of 2.5 µm. DCT projections were reconstructed using the commercial software GrainMapper3DTM developed by Xnovo Technology ApS. Back-scattered X-ray Laue diffraction was collected with a tungsten source operating at 10 kV and 10 mA with a Multiwire Laboratories MWL 110 real-time back-reflection Laue camera. The tool MuCalc (https://www.ctlab.geo.utexas.edu/software/mucalctool/) was used to plot attenuation versus X-ray energy, drawing data from the NIST XCOM database69. Crystal structures were visualized using Vesta software70.
Data availability
Raw data from the facility related to these experiments are available at https://doi.org/10.34863/sd37-3694.
References
National Research Council. Frontiers in Crystalline Matter: From Discovery to Technology (The National Academies Press, 2009).
Broholm, C. et al. Basic research needs workshop on quantum materials for energy relevant technology. https://doi.org/10.2172/1616509 (2016).
Sarrao, J. et al. Basic research needs for superconductivity. https://doi.org/10.2172/899129 (2006).
Thornton, P. A. The influence of nonmetallic inclusions on the mechanical properties of steel: a review. J. Mater. Sci. 6, 347–356 (1971).
Zhang, L. & Thomas, B. G. State of the art in the control of inclusions during steel ingot casting. Metall. Mater. Trans. B 37, 733–761 (2006).
Zhang, P. et al. Enhancing carrier transport properties of melt-grown CsPbBr3 single crystals by eliminating inclusions. Cryst. Growth Des. 20, 2424–2431 (2020).
Zhang, L. T., Tsutsui, M., Ito, K. & Yamaguchi, M. Effects of ZnSb and Zn inclusions on the thermoelectric properties of β-Zn4Sb3. J. Alloy. Comp. 358, 252–256 (2003).
Gurevich, A. & Pashitskii, E. A. Current transport through low-angle grain boundaries in high-temperature superconductors. Phys. Rev. B 57, 13878 (1998).
Durrell, J. H. & Rutter, N. A. Importance of low-angle grain boundaries in YBa2Cu3O7-δ coated conductors. Supercond. Sci. Technol. 22, 013001 (2009).
Maeno, Y. et al. Enhancement of superconductivity of Sr2RuO4 to 3 K by embedded metallic microdomains. Phys. Rev. Lett. 81, 3765–3768 (1998).
Jin, R., Zadorozhny, Yu. & Liu, Y. Observation of anomalous temperature dependence of the critical current in Pb/Sr2RuO4/Pb junctions. Phys. Rev. B 59, 4433–4438 (1999).
Ying, Y. A. et al. Enhanced spin-triplet superconductivity near dislocations in Sr2RuO4. Nat. Commun. 4, 2596 (2013).
Bianco, E. & Kourkoutis, L. F. Atomic-resolution cryogenic scanning transmission electron microscopy for quantum materials. Acc. Chem. Res. 54, 3277–3287 (2021).
Venables, J. A., Smith, D. J. & Cowley, J. M. HREM, STEM, REM, SEM-and STM. Surf. Sci. 181, 235–249 (1987).
Becker, J. S. & Dietze, H.-J. Inorganic trace analysis by mass spectrometry. Spectrochim. Acta B: . Spectrosc. 53, 1475–1506 (1998).
Stock, S. R. X-ray microtomography of materials. Int. Mater. Rev. 44, 141–164 (1999).
Ritman, E. L. Micro-computed tomography-current status and developments. Annu. Rev. Biomed. Eng. 6, 185–208 (2004).
Rawson, S. D., Maksimcuka, J., Withers, P. J. & Cartmell, S. H. X-ray computed tomography in life sciences. BMC Biol. 18, 21 (2020).
Hanna, R. D. & Ketcham, R. A. X-ray computed tomography of planetary materials: a primer and review of recent studies. Geochemistry 77, 547–572 (2017).
Vásárhelyi, L., Kónya, Z., Kukovecz, Á. & Vatjai, R. Microcomputed tomography-based characterization of advanced materials: a review. Mater. Today Adv. 8, 100084 (2020).
Phelan, W. A. et al. On the chemistry and physical properties of flux and floating zone grown SmB6 single crystals. Sci. Rep. 6, 20860 (2016).
Berry, T., Pressley, L. A., Phelan, W. A., Tran, T. T. & McQueen, T. M. Laser enhanced single crystal growth of non-symmorphic materials: applications to an eight-fold fermion candidate. Chem. Mater. 13, 5827–5834 (2020).
Sinha, M. et al. Twisting of 2D kagome sheets in layered intermetallics. ACS Cent. Sci. 7, 1381–1390 (2021).
ASTM. Standard guide for computed tomography (CT) imaging. in Annual Book of ASTM Standards, Section 3 Metals Test Methods and Analytical Procedures 690–713 (ASTM, 1992).
Rudolph, P. Defect formation during crystal growth from the melt. In Handbook of Crystal Growth (eds Dhanaraj, G., Byrappa, K., Prasad, V., Dudley, M.) 159–201 (Springer Heidelberg Dordrecht London New York, 2010).
Hu, Z. W. et al. Synchrotron topographic characterization of Fe-doped flux-grown Potassium Niobate Tantalate. Appl. Phys. Lett. 61, 648 (1992).
Sadrabadi, P. et al. Evolution of dislocation structure and deformation resistance in creep exemplified on single crystals of CaF2. Mater. Sci. Eng. A 510–511, 46–50 (2009).
Cockayne, B. Developments in melt-grown oxide crystals. J. Cryst. Growth 3–4, 60–70 (1968).
Wang, X., Wang, J., Yu, Y., Zhang, H. & Boughton, R. I. Growth of cubic KTa1-xNbO3 crystal by Czochralski method. J. Cryst. Growth 293, 398–403 (2006).
Polgár, K., Peter, À., Földvári, I. & Szaller, Z. Structural defects in flux-grown stoichiometric LiNbO3 single crystals. J. Cryst. Growth 218, 327–333 (2000).
Saeedi, H. et al. Thermal shocks influence on the growth process and optical quality of Nd: YAG crystal. J. Cryst. Growth 363, 171–175 (2013).
Föll, H. & Kolbesen, B. O. Formation and nature of swirl defects in silicon. Appl. Phys. 8, 319–331 (1975).
Falster, R. & Voronkov, V. V. The engineering of intrinsic point defects in silicon wafers and crystals. Mater. Sci. Eng. B 73, 87–94 (2000).
Montes, J. M., Rodríguez, J. A. & Herrera, E. J. Thermal and electrical conductivities of sintered powder compacts. Powder Met. 46, 251–256 (2013).
Rondinelli, J. M. et al. Accelerating functional materials discovery. Am. Ceram. Soc. Bull. 92, 9 (2013).
Phelan, W. A. et al. Adventures in crystal growth: synthesis and characterization of single crystals of complex intermetallic compounds. Chem. Mater. 24, 409–420 (2012).
Bugaris, D. E. & Loye, H.-C. Materials discovery by flux crystal growth: quaternary and higher order oxides. Angew. Chem. Int. Ed. 51, 3780–3811 (2012).
Canfield, P. C. & Fisk, Z. Growth of single crystals from metallic fluxes. Philos. Mag. B 65, 1117–1123 (1991).
Rosa, P. F. S. & Fisk, Z. Bulk and surface properties of SmB6. In Rare-Earth Borides (ed. Inosov, D.) 817–875 (Jenny Stanford Publishing, 2021).
Thomas, S. M. et al. Quantum oscillations in flux-grown SmB6 with embedded aluminum. Phys. Rev. Lett. 112, 166401 (2019).
Ketcham, R. A. Computational methods for quantitative analysis of three-dimensional features in geological specimens. Geosphere 1, 32–41 (2005).
Ketcham, R. A. Three-dimensional grain fabric measurements using high-resolution X-ray computer tomography. J. Struct. Geol. 2, 1217–1228 (2005).
Smit, Th. H., Schneider, E. & Odgaard, A. Star length distribution: a volume-based concept for the characterization of structural anisotropy. J. Microsc. 191, 249–257 (1998).
Naumann, M. et al. Fermi surface of the Skutterudite CoSb3: quantum oscillations and band-structure calculations. Phys. Rev. B 103, 085133 (2021).
Chae, S. et al. Toward the predictive discovery of ambipolarly dopable ultra-wide-band-gap semiconductors: the case of rutile GeO2. Appl. Phys. Lett. 118, 260501 (2021).
Niedermeier, C. A., Ide, K., Katase, T., Hosono, H. & Kamiya, T. Shallow valence band of rutile GeO2 and P-type doping. J. Phys. Chem. C. 124, 25721–25728 (2020).
Takane, H. & Kaneko, K. Establishment of a growth route of crystallized rutile GeO2 thin film (≧1 µm/h) and its structural properties. Appl. Phys. Lett. 119, 062104 (2021).
Morey, J. R. et al. Growth and characterization of iron scandium sulfide (FeSc2S4). J. Cryst. Growth 454, 128–133 (2016).
Yu, P. et al. Correlation between Te inclusions and the opto-electrical properties of CdMnTe and CdMgTe single crystals. J. Cryst. Growth 571, 126259 (2021).
Su, H. et al. Distribution control and formation mechanism of gas Inclusions in directionally solidified Al2O3-Er3Al5O12-ZrO2 ternary eutectic ceramic by laser floating zone melting. J. Mater. Sci. Technol. 66, 21–27 (2021).
Berry, T., Bernier, S., Auffermann, G., McQueen, T. M. & Phelan, W. A. Laser floating zone growth of SrVO3 single crystals. J. Cryst. Growth 583, 126518 (2022).
Dabkowska, H. A. & Dabkowski, A. B. Crystal growth of oxides by optical floating zone technique. In Springer Handbook of Crystal Growth (eds Dhanaraj, G., Byrappa, K., Prasad, V., Dudley, M.) 367–390 (Springer Heidelberg Dordrecht London New York, 2010).
Phelan, W. A., Zahn, J., Kennedy, Z. & McQueen, T. M. Pushing boundaries: high pressure, supercritical optical floating zone materials discovery. J. Sol. St. Chem. 270, 705–709 (2019).
Li, Y. et al. Rare-earth triangular lattice spin liquid: a single-crystal study of YbMgGaO4. Phys. Rev. Lett. 115, 167203 (2015).
Paddison, J. A. M. et al. Continuous excitations of the triangular-lattice quantum spin liquid YbMgGaO4. Nat. Phys. 13, 117–122 (2017).
Egan, C. K. et al. 3D chemical imaging in the laboratory by hyperspectral X-ray computed tomography. Sci. Rep. 5, 15979 (2015).
Ludwig, W. et al. Three-dimensional grain mapping by X-ray diffraction contrast tomography and the use of Friedel pairs in diffraction data analysis. Rev. Sci. Instrum. 80, 033905 (2009).
McDonald, S. A. et al. Microstructural evolution during sintering of copper particles studied by laboratory diffraction contrast tomography (LabDCT). Sci. Rep. 7, 5251 (2017).
Qu, K. et al. Morphology and growth habit of the new flux-grown layered semiconductor KBiS2 revealed by diffraction contrast tomography. Cryst. Growth Des. 22, 3228–3234 (2022).
Wright, C. J. ‘C. J. ’ et al. Toward in situ synchrotron mapping of crystal selection processes during crystal growth. Chem. Mater. 33, 3359–3367 (2021).
Higuchi, M., Hosokawa, T. & Kimura, S. Growth of rutile single crystals by floating zone method. J. Cryst. Growth 112, 354–358 (1991).
Hu, B. Q., Zhang, Y. Z., Wu, X. & Chen, X. L. Defects in large single crystals Nd:YVO4. J. Cryst. Growth 226, 511–516 (2001).
Witteveen, C. et al. Polytypism and superconductivity in the NbS2 system. Dalton Trans. 50, 3216–3223 (2021).
Sung, N. H. et al. Crystal growth and intrinsic magnetic behavior of Sr2IrO4. Philos. Mag. 96, 413–426 (2016).
Haynes, A. S., Stoumpos, C. C., Chen, H., Chica, D. & Kanatzidis, M. G. Panoramic synthesis as an effective materials discovery tool: the system Cs/Sn/P/Se as a test case. J. Am. Chem. Soc. 139, 10814–10821 (2017).
Xia, F. et al. Understanding solvothermal crystallization of mesoporous anatase beads by in situ synchrotron PXRD and SAXS. Chem. Mater. 26, 4563–4571 (2014).
Chae, S. et al. Germanium dioxide: a new rutile substrate for epitaxial film growth. J. Vac. Sci. Tech. A 40, 050401 (2022).
Ketcham, R. A. & Hildebrandt, J. Characterizing, measuring, and utilizing the resolution of CT imagery for improved quantification of fine-scale features. Nucl. Instrum. Methods Phys. Res. B: Beam Interact. Mater. 324, 80–87 (2014).
Berger, M. J. et al. XCOM: Photon cross sections database (version 1.5). [Online] Available: http://physics.nist.gov/xcom [2022, December 17] National Institute of Standards and Technology, Gaithersburg, MD (2010).
Momma, K. & Izumi, F. VESTA: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Cryst. 41, 654–658 (2008).
Acknowledgements
This work was funded by the Platform for the Accelerated Realization, Analysis, and Discovery of Interface Materials (PARADIM), a National Science Foundation Materials Innovation Platform (NSF DMR-2039380). The UTCT facility is partially supported by NSF grant EAR-176245 with funding for the Zeiss Versa 620 funded by NSF MRI grant EAR-1919700. Access to the Bruker 1172 instrument was also possible via the Hopkins Extreme Materials Institute (HEMI). L.A.P., T.M.M., and M.A.K. would like to thank Navindra Keerthisinghe, Vicky Li, Trent Kyrk, and Olivia Vilella for their group participation in the high-pressure floating zone growth of YbMgGaO4 at the 2021 PARADIM Summer School at JHU. L.A.P. would like to thank Jessica Maisano for assistance with DCT data collection, Juan Chamorro for helpful discussions and providing SmB6 samples for analysis, and Tanya Berry for conversations around applications of µCT.
Author information
Authors and Affiliations
Contributions
L.A.P., D.E., and R.H. performed µCT characterization and analysis. L.A.P., S.C., and J.T.H. conceived of and synthesized r-GeO2 samples. L.A.P. and M.A.K. synthesized YbMgGaO4 samples. T.M.M. supervised the work with the original conception coming from T.M.M. and L.A.P. All authors contributed to the writing and preparation of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pressley, L.A., Edey, D., Hanna, R. et al. Informing quantum materials discovery and synthesis using X-ray micro-computed tomography. npj Quantum Mater. 7, 121 (2022). https://doi.org/10.1038/s41535-022-00527-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-022-00527-6