Abstract
Electronic nematicity, the breaking of the crystal lattice rotational symmetry by the electronic fluid, is a fascinating quantum state of matter. In this work, using electronic transport under strain we investigate the electronic nematicity of BaNi2(As1−xPx)2, a candidate system for charge-induced nematicity. We report a large B1g elastoresistance coefficient that is maximized at the tetragonal-to-orthorhombic transition temperature, that slightly precedes the first-order triclinic transition. An hysteretic behavior is observed in the resistance versus strain sweeps and interpreted as the pinning of orthorhombic domains. Remarkably, the elastoresistance only onsets together with a strong enhancement of the incommensurate charge density wave of the material, strongly suggesting that this electronic instability is uniaxial in nature and drive the orthorhombic transition. The absence of sizeable elastoresistance above this electronic phase clearly contrasts dynamic and static electronic nematicity. Finally, the elastoresistance temperature dependence that strongly differs from the Curie-Weiss form of iron-based superconductors reveals major differences for the respective coupling of electronic nematicity to the lattice. Our results uncover an extremely strain-sensitive platform to study electronic anisotropy induced by a charge-density-wave instability.
Similar content being viewed by others
Introduction
With the discovery of iron-based superconductors1, electronic nematicity has emerged as a potential key ingredient for high-temperature superconductivity. Indeed, the observation of strong electronic nematic fluctuations at the optimal conditions for superconductivity suggests that such fluctuations might promote higher Tc2,3,4,5,6. This view is supported by reports for nematicity in other unconventional superconductors as heavy fermions7,8 or cuprates9,10,11,12,13,14,15.
Nonetheless, the best-understood case is by far the one of the iron pnictides, where the electronic nematic fluctuations induce a tetragonal-to-orthorhombic phase transition at Ts. The nematic transition, when not coincident with, is closely followed by antiferromagnetic order at TN16,17,18. From this empirical observation and theoretical considerations5 anisotropic magnetic fluctuations are a leading candidate for the mechanism of nematicity in iron-based superconductors. However, beyond the iron pnictides case, and in particular in the absence of long-range magnetic order19,20,21,22,23,24, much remains to be understood about the mechanisms of electronic nematicity and its significance for superconductivity.
In this regard, BaNi2As2, which shares the same high temperature tetragonal structure as the intensively studied BaFe2As2, has recently attracted attention. In contrast to its iron-analog, BaNi2As2 is superconducting below Tc ≈ 0.7 K at ambient pressure25 and hosts two types of charge density waves (CDWs). Upon cooling, first appears an incommensurate charge density wave (I-CDW) that develops strongly at T ≈ 155 K. A weaker diffuse signal can be tracked all the way up to room temperature26,27,28. The exact nature of this I-CDW is currently under intense investigation. The reciprocal space pattern of the I-CDW superlattice peaks reported by X-ray diffraction experiments indicated that the charge modulation is unidirectional26,27,29,30. Thus, it has been initially linked to a breaking of the crystal lattice rotational symmetry29,31. Although, from a wide reciprocal lattice mapping it has been later suggested that, overall, the I-CDW is a symmetric, biaxial, rotationally invariant state30, a clear rotational symmetry breaking has been recently observed within the I-CDW phase by high-resolution thermal expansion measurements26,32. At a slightly lower temperature, a commensurate uniaxial charge density wave (C-CDW) develops at the expense of the former26,27,28,29,30 and is associated with a first-order triclinic structural transition at Ttri ≈ 137 K. This latter coincident transition is suppressed through numerous chemical substitutions at a critical value, xc25,26,27,29,30,33,34.
Despite the absence of static magnetism down to the lowest investigated temperature35 possible indications for electronic nematicity have been reported. First, in Ba1−xSrxNi2As2 strain-dependent electrical transport measurements, namely elastoresistance, have been interpreted as a signature of a large B1g electronic nematic susceptibility upon approaching the triclinic phase transition in substituted samples31. Second, a continuous orthorhombic transition was recently found to precede the triclinic one in Ba(Ni1−xCox)2As2 and BaNi2(As1−xPx)226,32. Unlike in BaFe2As2 the in-plane orthorhombic axes are aligned with the tetragonal ones and the associated lattice distortion is much smaller. By analogy with the iron pnictides, it was proposed that this intermediate phase with broken rotational symmetry is a possible manifestation of charge-induced nematicity26.
In addition, the superconducting Tc has been found to sharply increase to ≈3 K for substitution levels just above the suppression of the triclinic and C-CDW transition, but the origin of this enhancement is still debated. In Ba1−xSrxNi2As2 it has been associated with electronic nematic fluctuations31, while in BaNi2(As1−xPx)2 it has been attributed to an enhanced electron-phonon coupling through a lattice softening34.
Thus, it is critically needed to assess the possible advent of electronic nematicity in these materials and establish its interplay with the aforementioned lattice and electronic instabilities. In this work, we investigate the electronic nematicity of BaNi2(As1−xPx)2 with 0 ≤ x ≤ 0.10, a system for which the tetragonal-to-orthorhombic transition is established26,32, using elastoresistance measurements. We report a large maximum of the B1g-symmetric elastoresistance coefficient, m12−m11, that occurs, up to x = 0.075, at the temperature of the orthorhombic transition, where the rotational symmetry is broken. Importantly, the elastoresistance onset corresponds to a strong increase in the I-CDW superlattice peak intensity that cannot be described by a Curie-Weiss-like temperature dependence and points to a minor coupling of electronic nematicity to the lattice. Thus, the anisotropic strain-dependent electrical transport is a property of the I-CDW phase and strongly suggests the latter as being uniaxial in nature. Importantly, dynamic nematic effects recently reported by Raman scattering27 significantly precede the unveiled static nematic susceptibility, consistent with a broad temperature range of dynamic anisotropic charge/orbital correlation prior to the static I-CDW. Finally, a careful investigation of the hysteretic behavior of the resistance versus strain sweeps strongly suggests that the hysteresis originates from the pinning of orthorhombic domains.
Results
Experimental details
We start by investigating the freestanding resistance of BaNi2(As1−xPx)2 single crystals in Fig. 1a. A metallic behavior with residual-resistivity ratio (RRR) values in line with the literature25,34 is observed. For BaNi2As2 RRR ≈ 12 i.e. approximately the value found in BaFe2As236. In agreement with previous reports, a sharp increase of electrical resistance occurs at Ttri = 137 K upon cooling in BaNi2As2, signaling the triclinic structural transition25,34. The hysteresis indicates the first-order nature of the transition. Upon increasing P-substitution this transition is shifted towards lower temperature, the resistance upturn becomes a downturn, and the width of the thermal hysteresis increases. No such transition is observed for x = 0.10, where cooling and warming measurements overlap, indicating a critical doping for the triclinic phase xc ≈ 0.08, in agreement with the literature27,32,34.
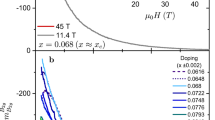
a Normalized resistance, R(T)/R(300K), at the indicated x values. Cooling and warming measurements are depicted as light and dark colors, respectively. The curves are vertically shifted for clarity. The arrows indicate the triclinic transition temperatures upon warming, and the dashed black line is a high temperature fit to R = R0 + ATn for T > Tonset (Tonset being the onset temperature of the elastoresistance, see main text). The inset shows the evolution of the n exponent on substitution level. b Schematic of an elastoresistance experiment: the sample (black rectangle) is glued on top of a piezo with its [100]tet axis along the piezo poling direction, x. Application of a positive voltage to the piezo leads to a tensile strain along the poling direction and a compression in the orthogonal axis through Poisson effect. Both Rxx (so-called longitudinal) and Ryy (transverse) electrical resistances are measured, using the piezo frame notation. The corresponding A1g + B1g strain state of the basal plane is also shown. c Representative resistance variation with strain in transverse geometry for x = 0 at selected temperatures. The elastoresistance signal is strongest at T* ≈ 146K while an hysteretic behavior is more pronounced at lower temperature.
At low temperature, and except at the highest (x = 0.10 > xc) P-content, the electrical resistance does not follow a T2 temperature dependence25,32 (see Supplementary Note 6 for more details). At high enough temperatures the resistance is well described as R = R0 + A × Tn (see dashed blacked line in Fig. 1a for x = 0.070), with A and n being x-dependent. As seen in the inset of Fig. 1a the exponent n shows a significant increase across the triclinic critical point, and in particular n ≈ 1, i.e., a linear-in-temperature resistance is observed within a narrow substitution range around xc, whose origin is still unknown (more details on the fitting are given in Supplementary Note 1).
In order to study the elastoresistance of BaNi2(As1−xPx)2, we induce an antisymmetric biaxial strain to our single crystals by gluing them on top of a piezo stack as visualized in Fig. 1b, a technique initially used in strongly correlated systems in ref. 2. This method allows to extract the elastoresistance coefficients defined as mii,jj = 1/Rii(dRii/dϵjj), where j denotes the direction of the strain and i = x (resp. i = y) corresponds to longitudinal (resp. transverse) measurements with respect to the piezo poling axis, x. In the following, we use the Voigt notation for the elastoresistance coefficient, in particular xx = 1 and yy = 2, and formulate in terms of the irreducible representations of the high-temperature D4h tetragonal point group.
With the [100]tet axis aligned to the piezo stack poling direction, as done in the following, the in-plane resistance anisotropy that develops under strain is proportional to the symmetry-resolved B1g elastoresistance coefficient, m12−m11,
Since for sufficiently small anisotropy any potential electronic nematic order parameter is proportional to the resistance anisotropy, the associated electronic nematic susceptibility in the B1g channel is probed by the m12−m11 elastoresistance coefficient2,31,37,38.
Elastoresistance of BaNi2As2
A typical example of raw data in BaNi2As2 in the transverse geometry is shown in Fig. 1c. The corresponding detailed temperature dependence of the elastoresistance measurement is reported in Fig. 2.
a Normalized electrical resistances recorded with the sample [100]tet axis glued along the poling direction of the piezo. Longitudinal (i = x, orange squares) and transverse measurements (i = y, dark red circles) correspond to resistances measured along and perpendicular to the piezo poling axis, respectively. No voltage is applied to the piezo. For comparison the freestanding resistance from Fig. 1a is added (dark and light red lines for warming and cooling measurements, respectively). b Corresponding slopes of the normalized resistance versus strain variation, 1/Rii(dRii/dϵxx), obtained through sweeping the piezo voltage at fixed temperatures. The filled (respectively empty) symbols correspond to cooling (resp. warming) measurements. The gray shaded area shows the temperature range of the triclinic structural transition upon cooling, while the vertical line denotes Torth, i.e., the orthorhombic transition temperature as determined by thermal expansion26,32. The temperature of the maximum of the elastoresistance, T*, is consistent with Torth. Lines are guide to the eye.
First, we show the normalized resistances as a function of temperature with the sample being glued to the piezo, see Fig. 2a. While both longitudinal and transverse directions (squares and circles, respectively) overlap at high enough temperature, a clear discrepancy appears below T ≈ 145 K, that corresponds to the second-order orthorhombic transition temperature, Torth, as determined by thermal expansion measurements26,32. This observation evidences that, within the orthorhombic state, the sample is, at least partially, detwinned through the anisotropic thermal expansion of the piezo (see Supplementary Note 2) and the resulting strain.
The normalized freestanding resistance (dark and light red lines for the warming and cooling measurement, respectively), reproduced from Fig. 1a, also overlaps with that of the sample glued to the piezo down to ≈160 K. However, at lower temperatures, a difference appears which can be attributed to the differential thermal expansion of the piezo and BaNi2As2 together with the emergence of a finite elastoresistance. The similar resistivity values observed in the longitudinal and transverse channels down to Torth are also in line with the mainly in-plane isotropic strain arising from the thermal expansion mismatch (see details in Supplementary Note 2) and points to a finite in-plane symmetric elastoresistance.
While the gluing induces a broadening of the triclinic transition as seen by electrical transport, a thermal hysteresis is still clearly observed in these strained conditions and the transition temperature is not substantially shifted. Finally, note that the sign of the resistance anisotropy in the orthorhombic state is similar to the one in BaFe2As2, i.e., the smaller in-plane orthorhombic axis (aligned with the y piezo axis) is the one with the higher resistivity36,37.
The linear slopes of the resistance versus strain sweeps, 1/Rii(dRii/dϵxx), are reported in Fig. 2b. Note that they are extracted during the same temperature cycle as the corresponding resistances of Fig. 2a, upon applying a voltage to the piezo stack at fixed temperatures. At high temperature, no response to strain is seen in any channel, in agreement with the overlap of the respective electrical resistances. However, below Tonset ≈ 160 K an elastoresistance signal develops sharply in both directions and peaks at T* = 145 ± 2 K ≈ Torth, with an opposite sign along the two directions. Thus, the B1g symmetric m12−m11 elastoresistance coefficient extracted from the difference of the longitudinal and transverse measurements is maximum at T* ≈ Torth (see Eq.(1) and Fig. 3a; in the followings, T* is formally defined as the temperature of the m12−m11 maximum). Notably, no strong feature appears at the triclinic transition temperature. This brings us to our first important result: the B1g-symmetric m12−m11 maximum occurs at the orthorhombic transition rather than at the triclinic one, in contrast to what has been previously reported for Sr-substituted samples31. This is fully consistent with the 4-fold symmetry breaking that occurs at the orthorhombic transition26,32 and the absence of thermal hysteresis in the elastoresistance response, in particular around T* (see also additional measurements in Supplementary Fig. 4).
a–d B1g symmetry-resolved m12−m11 elastoresistance coefficient (filled circles, left axis) together with the integrated intensity of the I-CDW satellite at QI-CDW = (4 0.72 1)tet (empty squares, right axis, reproduced from ref. 27), for different x values as indicated. Both quantities are shown upon cooling, except for the x = 0.10 X-ray diffraction (XRD) data, and plotted as a function of T−Ttri, where the triclinic transition temperature is measured upon cooling. No triclinic phase is observed at x = 0.10 and thus the data are as a function of T in d. The gray area represents the width of the triclinic transition as determined from the elastoresistance samples (see Supplementary Note 5). Note that elastoresistance and XRD measurements are performed on different samples that share similar triclinic transition temperatures, except for x = 0.075 where the XRD sample has a slightly lower P-content and accordingly higher Ttri ≈ 55K. The arrows indicate the onset temperature of m12−m11, Tonset, and the temperature of the elastoresistance maximum, T*. In the inset of a the B2g-symmetric−m66 elastoresistance coefficient of BaFe2As2 from ref. 42 (black diamonds, vertically scaled) is compared to the m12−m11 coefficient of BaNi2As2. Lines are guides to the eye.
Evolution with P-concentration
The m12−m11 elastoresistance coefficient at the different P-contents investigated is shown in Fig. 3b–d, as a function of T−Ttri, where the triclinic transition temperature and the elastoresistance coefficient are extracted upon cooling. A maximum of the elastoresistance is found up to the highest concentration investigated at temperature exceeding the triclinic transition. Rather, up to x = 0.075, T* is in good agreement with Torth as determined by thermal expansion. With increasing substitution level, T* decreases smoothly towards T* ≈ 50 K for x = 0.10 where the associated elastoresistance maximum becomes weaker and significantly broader. In particular, there is no enhancement of m12−m11 associated with the enhanced superconducting Tc in the absence of the triclinic structure for x = 0.10. Note that for x = 0.10 no orthorhombic distortion is observed by high-resolution thermal expansion, which shows however a clear signature of a (different) first-order transition32. This is most likely not directly related to the elastoresistance maximum since, as for lower P-contents, no evidence for a thermal hysteresis is observed. We discuss this particular case later.
A fundamental aspect is the comparison between the temperature dependences of the m12−m11 elastoresistance coefficient and of the I-CDW superlattice peak intensity recorded at QI-CDW = (4 0.72 1)tet (empty squares, reproduced from ref. 27). Using samples from the same batches across the entire substitution range investigated, we find that both quantities onset at very similar temperatures. The elastoresistance coefficient is negligible above Tonset, that corresponds to a strong increase in the I-CDW superlattice peak intensity, but significantly precedes the rotational symmetry breaking at Torth < Tonset32. Thus, a large m12−m11 coefficient is a property of the incommensurate charge density wave phase and the associated fluctuations.
Finally, the maximum value of the m12−m11 elastoresistance coefficient displays a non-monotonic dependence on P-concentration and is highest at x = 0.035, an observation that is reminiscent of Ba1−xSrxNi2As231. While this might be an artifact of strain transmission, one possible alternative scenario, that remains to be investigated, is a stronger orthorhombic distortion at this particular substitution content.
Strain hysteresis
A peculiar feature of the reported elastoresistance is the presence of reproducible hysteresis in the resistance versus strain sweeps (see Fig. 1c). This was previously reported in Ba1−xSrxNi2As2 and attributed to the pinning of static nematic domains by the I-CDW30,31. Similar hysteresis behavior was also observed in RTe3 (R= Tm, Er) and ascribed to a first-order reorientation of the CDW wavevector with uniaxial stress39.
In Fig. 4 we report the evolution of the hysteresis width, i.e., the maximum difference of the relative resistance variation between the up and down strain sweeps (see inset), as a function of P-substitution and temperature. In all samples at high temperature no hysteresis is seen, i.e., the response of electrical resistance to strain appears perfectly reversible. In that case, we can only define an upper limit on the unresolved and/or non-existent hysteresis width based on the experimental noise. This is depicted as vertical error bars extending to zero. Below a substitution-dependent temperature, a finite hysteresis is resolved, meaning in particular that the hysteresis width is larger than the experimental noise. Note that only for x = 0.10 no finite hysteresis is resolved down to the lowest temperature (see Supplementary Note 4).
Temperature dependence of the hysteresis width for the indicated compositions. The inset shows the definition of the hysteresis width, i.e., the maximum difference between the up and down strain sweeps, shown here for x = 0.075 at T = 70 K in the transverse geometry. For a given x value, the hysteresis width shown corresponds to the (transverse or longitudinal) measurement with the best signal-to-noise ratio. At any given temperature we report the value obtained from an average of several strain sweeps, the positive (resp. negative) error bars are extracted from the maximal (resp. minimal) value of individual strain sweeps. At temperatures where no hysteresis is resolved, the hysteresis width has to be smaller than the experimental noise and this is shown as a positive error bar extending down to zero. The arrows indicate the corresponding T* temperatures of maximum m12−m11 (see Fig. 3). For x = 0.10 no finite hysteresis is resolved down to the lowest temperature.
For all other substitution levels, we observe a rather sharp increase of the hysteresis width across the T* temperature of maximum elastoresistance (see arrows). While for BaNi2As2 a finite hysteresis is found to emerge at T ≈ Tonset within resolution, in agreement with ref. 31, this is not the case in P-substituted samples. Since the hysteresis width significantly increases across T* for 0 ≤ x ≤ 0.075 one likely scenario is that the hysteresis is associated to the pinning of orthorhombic domains. This is consistent with the orthorhombic domains orientation26. Testing this scenario would require measurements under larger strain and a precise knowledge of the temperature and substitution dependencies of the spontaneous orthorhombic distortion40. The remarkable absence of a finite hysteresis at x = 0.10 might be a signature of the absence of the orthorhombic distortion, of which the absence of detwinning effect seen in thermal expansion measurements is a more direct evidence32. Finally, the hysteretic strain behavior persists into the triclinic phase where the associated structural and/or C-CDW domains probably play a major role.
Discussion
We summarize our results in a phase diagram, see Fig. 5. A large m12−m11 elastoresistance coefficient onsets together with a strong enhancement of the I-CDW satellite intensity and has a maximum at the orthorhombic transition up to x = 0.075. Remarkably, this elastoresistance onset also corresponds to a maximum in the crystallographic c/a ratio which occurs at the Tcross temperature reproduced from ref. 32. At x = 0.10, even though no orthorhombic transition has been reported by high-resolution thermal expansion32 a weaker and broader m12−m11 maximum is found. In parallel, the hysteretic behavior of the elastoresistance reported at lower substitution levels is not resolved anymore. Notably, upon increasing substitution level, the enhanced superconducting Tc above the triclinic critical point coincides with a reduction of m12−m11, and not an enhancement. Together with the already Tc ≈ 3 K superconductivity of fully substituted BaNi2P241, this observation strongly suggests that the superconductivity of BaNi2(As1−xPx)2 with x > xc is not significantly boosted by electronic nematicity.
Color map phase diagram showing the (B1g) m12−m11 elastoresistance coefficient. The onset of the elastoresistance signal, Tonset (empty circles), and the parallel strong increase in the I-CDW superlattice peak intensity as determined by X-ray experiments27, are in good agreement with Tcross (empty squares) that denotes a maximum in the c/a ratio32. Tc is the superconducting critical temperature as determined by specific heat27 (multiplied by a factor 10 for clarity; triangles, magenta area). T* (stars) denotes the m12−m11 maximum, in good agreement with Torth as determined by thermal expansion (closed circles, from ref. 32). Ttri (closed squares) is the triclinic transition temperature determined from freestanding resistance measurements upon cooling. Lines are guide to the eye.
We now consider in more detail the elastoresistance signal itself. The advent of a large B1g elastoresistance response maximized across the tetragonal-to-orthorhombic transition of BaNi2(As1−xPx)2 is certainly reminiscent of the electronic nematic transition of its iron-counterpart, BaFe2As2. However, there are fundamental differences between these two cases, which are highlighted in the following.
In the iron pnictides the m66 elastoresistance coefficient, probing nematicity in the B2g channel, follows a typical Curie–Weiss dependence over a wide temperature range of up to 100 K or more above the orthorhombic transition. Such a temperature dependence is expected on theoretical grounds from the coupling of an electronic nematic order parameter to a lattice strain of the same symmetry2,36,37,42. This temperature dependence is also observed above the nematic transition of FeSe1−xSx whose spin and/or orbital origin is still debated19,24,43. In sharp contrast, in BaNi2As2, m12−m11, probing nematicity in the B1g channel, increases only in the close vicinity of the orthorhombic transition and its onset corresponds to a strong increase in the I-CDW superlattice peak intensity seen in x-ray diffraction experiments. The difference is evident in the comparison shown in the inset of Fig. 3a where BaFe2As2 is chosen as it shares a close orthorhombic transition temperature. While for the latter compound the m66 elastoresistance coefficient can be tracked up to 150 K above the nematic transition, for BaNi2As2 m12−m11 ~ 1 only 20 K above Torth. Hence, in BaNi2As2 the temperature dependence of the elastoresistance is very different from that of the well-established electronic nematic systems, and in particular points to a minor coupling of electronic nematicity to the lattice. Moreover, while in the iron-based compound only the rotational symmetry is broken at Torth, in the nickel-based compound this may coincide with the I-CDW translational symmetry breaking44,45. In this latter scenario, there is no static electronic nematic order in BaNi2As2 in a strict sense since rotational and translational symmetries are broken simultaneously.
With increasing substitution level, the m12−m11 maximum broadens, which can be ascribed to the broadening of the orthorhombic distortion seen in thermal expansion32, the increasing disorder, and finally, the effect of external stress applied across the orthorhombic transition from the thermal expansion mismatch with the piezo. The latter effect is significant when the externally applied strain is of the same order as the spontaneous orthorhombic distortion. We expect this situation to be realized in BaNi2(As1−xPx)2 where, within our experimental conditions, both quantities are ~10−426,27,32 (see thermal expansion measurements in Supplementary Note 2). In addition, as for x = 0, the m12−m11 elastoresistance coefficient onsets together with a strong increase in the I-CDW satellite intensity and grows upon approaching the rotational symmetry breaking, advocating for a similar origin. Moreover, even in substituted samples, a Curie-Weiss susceptibility cannot fairly describe m12−m11 over a significant temperature range (more details in Supplementary Note 7). Thus, in pure and P-substituted samples, the large m12−m11 elastoresistance coefficient is not an evidence for critical electronic nematicity, but is a property of the I-CDW phase. We note that the absence of a significant critical electronic nematicity is consistent with Young modulus measurements at x = 0.1032 and an ARPES study of BaNi2As2 under uniaxial stress46. Finally, it is noteworthy to mention that the elastoresistance onsets at temperature significantly lower than the broadening and subsequent splitting of the Eg,1 phonon mode seen by Raman scattering and ascribed to dynamic electronic nematicity27. This difference points to a broad temperature range of dynamic anisotropic charge/orbital correlation preceding the static I-CDW order, a conclusion which is supported by recent inelastic x-ray scattering experiments44,45.
Let us now consider in more detail the parallel strong increase of the I-CDW superlattice peak intensity and the onset of the m12−m11 elastoresistance coefficient. Assuming that the temperature dependence of the electron-phonon coupling does not play a pivotal role, as suggested by several works26,27,32, this observation points to a direct connection between the I-CDW and the B1g elastoresistance.
Regardless of the exact mechanism of formation of the I-CDW, perturbation of the charge-ordered state can be achieved when strain of the right symmetry is applied39,47 and a corresponding electrical transport signature is expected through, for instance, modification of the Fermi surface48. Consequently, our observation of a large m12 − m11 elastoresistance coefficient only together with a strong enhancement of the I-CDW satellite intensity points towards a coupling between the I-CDW order parameter, the associated fluctuations, and the ϵxx−ϵyy strain, that strongly advocates for an uniaxial nature of the I-CDW. In particular, no significant B1g elastoresistance is expected to result from a symmetric biaxial I-CDW with very similar modulations along and perpendicular to the tetragonal a-axis, as ϵxx and ϵyy strains should perturb the I-CDW in an identical manner. In turn, this observation strongly suggests an intimate relationship of the I-CDW with the orthorhombic distortion, that manifests itself as a m12−m11 maximum, and that we interpret as a signature of the long-range order of the I-CDW. Importantly, this contrasts with Ba1−xSrxNi2As2 where, for x ≳ 0.5, a large m12−m11 elastoresistance coefficient occurs in the absence of the I-CDW phase and where, additionally, the fate of the orthorhombic phase remains to be investigated29,30,31. Our results, in particular the significant sensitivity of the I-CDW to uniaxial stress, put strong constraints on the theoretical description of this phase. It should motivate a refinement of its real space structure and spectroscopic studies under uniaxial stress. Another promising avenue is the recently developed in-situ combination of strain-dependent x-ray diffraction and electrical transport measurements49. Further elastoresistance studies in CDW systems, where a Curie-Weiss dependence is generally not observed39,50, are also highly desirable to investigate the different mechanisms at play.
Finally, we focus on a particularly intriguing case, BaNi2(As0.9P0.1)2, located above the triclinic critical point, xc. As for lower substitution levels, the onset of m12−m11 does correspond to a strong increase in the I-CDW superlattice peak intensity. Thus, it is very likely that, as for lower P-contents, the B1g elastoresistance reflects the growth of the I-CDW. However, as shown in Fig. 4 a strain hysteresis is not resolved at this substitution content anymore. In parallel, no detwinning of the orthorhombic domains is seen in high-resolution thermal expansion measurements, questioning the occurrence of an orthorhombic phase transition for this composition. A first-order transition is observed in thermal expansion within the temperature range of the m12−m11 maximum32, but the absence of a thermal hysteresis in the elastoresistance points toward a different origin. Moreover, the resistance measurements do not reveal any evidence of a phase transition in the vicinity of T* ≈ 50 K (see Supplementary Fig. 7). Noteworthy, the onset of the m12−m11 elastoresistance coefficient coincides with a lattice softening as seen by Young modulus measurements, which is argued to be incompatible with critical electronic nematicity32. The simultaneous maximum of elastoresistance and saturation of the softening below ≈ 50 K strongly suggests a close relationship between those two. The m12−m11 maximum, though broad, in the (likely) absence of an orthorhombic transition calls for further investigations.
In conclusion, we report that the I-CDW instability of BaNi2(As1−xPx)2 is extremely sensitive to antisymmetric biaxial strain. Specifically, we observe a large B1g-symmetric elastoresistance that strongly advocates for an I-CDW uniaxial in nature. Although the elastoresistance maximum at the tetragonal-to-orthorhombic transition is certainly reminiscent of the iron pnictides, the temperature dependence of m12−m11 is unprecedented and strikingly contrasts with known examples of electronic nematic transitions. In particular, the absence of a Curie-Weiss-like form points to a smaller coupling of electronic nematicity to the lattice as compared to the iron-based superconductors. The absence of significant B1g elastoresistance above Tonset, where a pronounced Eg,1 phonon broadening is observed by Raman scattering, clearly contrasts the static and dynamic electronic nematicity. Importantly, the weakening of the m12−m11 elastoresistance coefficient observed in parallel to the enhanced superconducting Tc in the absence of the triclinic structure evidence that the strain-sensitive electronic correlations revealed by elastoresistance are not responsible for the stronger superconductivity. Finally, a careful inspection of the hysteretic behavior of the resistance versus strain sweeps points to the pinning of orthorhombic domains as a likely origin.
Methods
Single crystals growth and chemical analysis
Single crystals of BaNi2(As1−xPx)2 (with x = 0, 0.035, 0.07, 0.075, 0.10) were grown using a self-flux method. NiAs binary was synthesized by mixing the pure elements Ni (powder, Alfa Aesar 99.999%) and As (lumps, Alfa Aesar 99.9999%) that were ground and sealed in a fused silica tube and annealed for 20 h at 730 ∘C. All sample handlings were performed in an argon glove box (O2 content <0.5 ppm). For the growth of BaNi2(As1−xPx)2, a ratio of Ba:NiAs:Ni:P = 1:4(1−x):4x:4x was placed in an alumina tube, which was sealed in an evacuated quartz ampule (i.e., 10−5 mbar). The mixtures were heated to 500–700 ∘C for 10 h, followed by heating slowly to a temperature of 1100–1180 ∘C, soaked for 5 h, and subsequently cooled to 1000–900 ∘C at the rate of 0.5 ∘C/h to 2 ∘C/h, depending on the phosphorus content used for the growth. At 1000–900 ∘C, the furnace was canted to remove the excess flux, followed by furnace cooling. Plate-like single crystals with typical sizes 3 × 2 × 0.5 mm3 were easily removed from the remaining ingot. The crystals were brittle having shiny brass-yellow metallic luster. Electron micro probe analysis of the BaNi2(As1−xPx)2 crystals was performed using a compact scanning electron microscope (SEM)—energy dispersive x-ray spectroscopy (EDS) device COXEM EM-30plus equipped with an Oxford Silicon-Drift-Detector (SDD) and AZtecLiveLite-software package. The EDS analyses on the BaNi2(As1−xPx)2 crystals revealed phosphorus content x = 0, 0.035, 0.070, 0.075, and 0.10 with a typical uncertainty of Δx = ± 0.05.
Elastoresistance measurements
DC-elastoresistance measurements were performed following the method described in ref. 38. We used piezoelectrics from Piezomechanik GmbH (Part. No. Pst 150/5 × 5 × 7) and miniature strain gauges from Vishay Precision Group. The samples and strain gauges were glued to opposites faces of the piezo using DevCon 5mn 2-components epoxy (Part. No. X0039). Bias voltages from +150 V to −30 V were used. The maximal strain ϵxx applied along the piezo poling direction decreases with decreasing temperature, going from ~ 0.1% at 300 K to less than ~0.03% at 50 K. The experimental setup has been checked and validated by measuring the well-known longitudinal response of BaFe2As22. To extract the symmetry-resolved m11−m12 elastoresistance coefficient we consider a temperature-independent piezo stack Poisson ratio ν = − ϵyy/ϵxx ≈ 0.4338.
The single crystals were cut with edges along the [100]tet direction, with typical dimensions 1.5 mm × 1 mm × 50 μm. The small thickness along the [001]tet direction is necessary for high and homogeneous strain transmission. The strain value extracted from the strain gauge is considered as the strain felt by the sample. A standard 4-contact geometry was used to measure the electrical resistance along the [100]tet direction using a Lake Shore 372 resistance bridge. For BaNi2As2, although we used an 8-contact geometry to extract the longitudinal and transverse elastoresistance during the same temperature cycle, each channel was measured one after the other, i.e., with current flowing along only one direction at a given time. As shown in Supplementary Fig. 4, this method gives very similar results compared to standard 4-contact geometry differential elastoresistance measurements. For P-substituted samples standard differential elastoresistance experiments were performed. Some of the freestanding resistance measurements were also done using a combination of Keithley 6221 current source and Keithley 2182A nanovoltmeter in delta mode. Either DuPont 4929N or Hans Wolbring Leitsilber silver paints were used.
Several strain sweeps were performed at each temperature to ensure the reproducibility of the extracted elastoresistance coefficients. A slow rate of 6 V/s was used to drive the piezo. If possible cooling and warming elastoresistance measurements were recorded, without any significant difference. All the presented elastoresistance coefficients are extracted from linear-in-strain fits. Second-order fits do not lead to any significant change in the extracted first-order coefficients.
Data availability
All relevant data are available from the corresponding author upon reasonable request.
References
Kamihara, Y. et al. Iron-based layered superconductor: LaOFeP. J. Am. Chem. Soc. 128, 10012–10013 (2006).
Chu, J.-H., Kuo, H.-H., Analytis, J. G. & Fisher, I. R. Divergent nematic susceptibility in an iron arsenide superconductor. Science 337, 710–712 (2012).
Kuo, H.-H. et al. Ubiquitous signatures of nematic quantum criticality in optimally doped Fe-based superconductors. Science 352, 958–962 (2016).
Böhmer, A. E. et al. Nematic Susceptibility of hole-doped and electron-doped BaFe2As2 iron-based superconductors from shear modulus measurements. Phys. Rev. Lett. 112, 047001 (2014).
Fernandes, R. M., Chubukov, A. V. & Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 10, 97–104 (2014).
Lederer, S., Schattner, Y., Berg, E. & Kivelson, S. A. Enhancement of superconductivity near a nematic quantum critical point. Phys. Rev. Lett. 114, 097001 (2015).
Ronning, F. et al. Electronic in-plane symmetry breaking at field-tuned quantum criticality in CeRhIn5. Nature 548, 313–317 (2017).
Okazaki, R. et al. Rotational symmetry breaking in the hidden-order phase of URu2Si2. Science 331, 439–442 (2011).
Murayama, H. et al. Diagonal nematicity in the pseudogap phase of HgBa2CuO4+δ. Nat. Commun. 10, 3282 (2019).
Daou, R. et al. Broken rotational symmetry in the pseudogap phase of a high-Tc superconductor. Nature 463, 519–522 (2010).
Sato, Y. et al. Thermodynamic evidence for a nematic phase transition at the onset of the pseudogap in YBa2Cu3Oy. Nat. Phys. 13, 1074–1078 (2017).
Cyr-Choinière, O. et al. Two types of nematicity in the phase diagram of the cuprate superconductor YBa2Cu3Oy. Phys. Rev. B 92, 224502 (2015).
Auvray, N. et al. Nematic fluctuations in the cuprate superconductor Bi2Sr2CaCu2O8+δ. Nat. Commun. 10, 5209 (2019).
Ishida, K. et al. Divergent nematic susceptibility near the pseudogap critical point in a cuprate superconductor. J. Phys. Soc. Jpn. 89, 064707 (2020).
Kivelson, S. A., Fradkin, E. & Emery, V. J. Electronic liquid-crystal phases of a doped Mott insulator. Nature 393, 550–553 (1998).
Nandi, S. et al. Anomalous suppression of the orthorhombic lattice distortion in superconducting \({{{\rm{Ba}}}}{({{{{\rm{Fe}}}}}_{1-x}{{{{\rm{Co}}}}}_{x})}_{2}{{{{\rm{As}}}}}_{2}\) single crystals. Phys. Rev. Lett. 104, 057006 (2010).
Ni, N. et al. Effects of Co substitution on thermodynamic and transport properties and anisotropic Hc2 in Ba(Fe1−x Cox)2 As2 single crystals. Phys. Rev. B 78, 214515 (2008).
Böhmer, A. E. et al. Thermodynamic phase diagram, phase competition, and uniaxial pressure effects in BaFe2(As1−xPx)2 studied by thermal expansion. Phys. Rev. B 86, 094521 (2012).
He, M. et al. Evidence for short-range magnetic order in the nematic phase of FeSe from anisotropic in-plane magnetostriction and susceptibility measurements. Phys. Rev. B 97, 104107 (2018).
Massat, P. et al. Charge-induced nematicity in FeSe. Proc. Natl Acad. Sc. 113, 9177–9181 (2016).
Chibani, S. et al. Lattice-shifted nematic quantum critical point in FeSe1−xSx. npj Quantum Mater. 6, 37 (2021).
Böhmer, A. E. et al. Lack of coupling between superconductivity and orthorhombic distortion in stoichiometric single-crystalline FeSe. Phys. Rev. B 87, 180505 (2013).
Ghini, M. et al. Strain tuning of nematicity and superconductivity in single crystals of FeSe. Phys. Rev. B 103, 205139 (2021).
Hosoi, S. et al. Nematic quantum critical point without magnetism in FeSe superconductors. Proc. Natl Acad. Sc. 113, 8139–8143 (2016).
Sefat, A. S. et al. Structure and anisotropic properties of BaFe2−xNixAs2 (x = 0, 1, and 2) single crystals. Phys. Rev. B 79, 094508 (2009).
Merz, M. et al. Rotational symmetry breaking at the incommensurate charge-density-wave transition in Ba(Ni, Co)2(As, P)2: Possible nematic phase induced by charge/orbital fluctuations. Phys. Rev. B 104, 184509 (2021).
Yao, Y. et al. An electronic nematic liquid in BaNi2As2. Nat. Commun. 13, 4535 (2022).
Pokharel, A. R. et al. Dynamics of collective modes in an unconventional charge density wave system BaNi2As2. Commun. Phys. 5, 141 (2022).
Lee, S. et al. Unconventional charge density wave order in the pnictide superconductor \({{{\rm{Ba}}}}{({{{{\rm{Ni}}}}}_{1-x}{{{{\rm{Co}}}}}_{x})}_{2}{{{{\rm{As}}}}}_{2}\). Phys. Rev. Lett. 122, 147601 (2019).
Lee, S. et al. Multiple charge density waves and superconductivity nucleation at antiphase domain walls in the nematic pnictide Ba1−xSrxNi2As2. Phys. Rev. Lett. 127, 027602 (2021).
Eckberg, C. et al. Sixfold enhancement of superconductivity in a tunable electronic nematic system. Nat. Phys. 16, 346–350 (2020).
Meingast, C. et al. Charge density wave transitions, soft phonon, and possible electronic nematicity in \({{{{\rm{BaNi}}}}}_{2}{({{{{\rm{As}}}}}_{1-x}{{{{\rm{P}}}}}_{x})}_{2}\). Phys. Rev. B 106, 144507 (2022).
Kudo, K., Takasuga, M. & Nohara, M. Copper doping of BaNi2As2: giant phonon softening and superconductivity enhancement. Preprint at https://arxiv.org/abs/1704.04854v1. (2017).
Kudo, K. et al. Giant phonon softening and enhancement of superconductivity by phosphorus doping of BaNi2As2. Phys. Rev. Lett. 109, 097002 (2012).
Kothapalli, K. et al. Single-crystal neutron diffraction studies on Ni-based metal-pnictide superconductor BaNi2As2. J. Phys.: Conf. Ser. 251, 012010 (2010).
He, M. et al. Dichotomy between in-plane magnetic susceptibility and resistivity anisotropies in extremely strained BaFe2As2. Nat. Commun. 8, 504 (2017).
Chu, J.-H. et al. In-plane resistivity anisotropy in an underdoped iron arsenide superconductor. Science 329, 824–826 (2010).
Kuo, H.-H., Shapiro, M. C., Riggs, S. C. & Fisher, I. R. Measurement of the elastoresistivity coefficients of the underdoped iron arsenide Ba(Fe0.975Co0.025)2As2. Phys. Rev. B 88, 085113 (2013).
Straquadine, J. A. W., Ikeda, M. S. & Fisher, I. R. Evidence for realignment of the charge density wave state in ErTe3 and TmTe3 under uniaxial stress via elastocaloric and elastoresistivity measurements. Phys. Rev. X 12, 021046 (2022).
Bartlett, J. M. et al. Relationship between transport anisotropy and nematicity in FeSe. Phys. Rev. X 11, 021038 (2021).
Mine, T. et al. Nickel-based phosphide superconductor with infinite-layer structure, BaNi2P2. Solid State Commun. 147, 111–113 (2008).
Palmstrom, J. C. et al. Critical divergence of the symmetric (A1g) nonlinear elastoresistance near the nematic transition in an iron-based superconductor. Phys. Rev. B 96, 205133 (2017).
Watson, M. D. et al. Emergence of the nematic electronic state in FeSe. Phys. Rev. B 91, 155106 (2015).
Song, Y. et al. Phonon softening and slowing down of charge-density-wave fluctuations in BaNi2As2. Preprint at https://arxiv.org/abs/2207.03289 (2022).
Souliou, S. M. et al. Soft-phonon and charge-density-wave formation in nematic BaNi2As2. Preprint at https://arxiv.org/abs/2207.07191 (2022).
Guo, Y. et al. Spectral evidence for unidirectional charge density wave in detwinned BaNi2As2. Preprint at https://arxiv.org/abs/2205.14339 (2022).
Johannes, M. D. & Mazin, I. I. Fermi surface nesting and the origin of charge density waves in metals. Phys. Rev. B 77, 165135 (2008).
Sinchenko, A. A., Grigoriev, P. D., Lejay, P. & Monceau, P. Spontaneous breaking of isotropy observed in the electronic transport of rare-earth tritellurides. Phys. Rev. Lett. 112, 036601 (2014).
Sanchez, J. J. et al. The transport-structural correspondence across the nematic phase transition probed by elasto X-ray diffraction. Nat. Mater. 20, 1519–1524 (2021).
Nie, L. et al. Charge-density-wave-driven electronic nematicity in a kagome superconductor. Nature 604, 59–64 (2022).
Acknowledgements
We thank R. Willa, I. Vinograd, and F. Hardy for valuable discussions. We acknowledge support by the Deutsche Forschungsgemeinschaft (DFG; German Research Foundation) under CRC/TRR 288 (Projects B03 and A02) and the Helmholtz Association under Contract No. VH-NG-1242. M.F. acknowledges funding from the Alexander von Humboldt Foundation and the Young Investigator Group preparatory program of the Karlsruhe Institute for Technology. K.W. acknowledges funding from the Swiss National Science Foundation through the postdoc mobility fellowship. S.M.S. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - Projektnummer 441231589.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
M.F., M.L.T., and A.E.B. initiated the elastoresistance project. T.L. and A.-A.H. grew the single-crystal samples and performed the EDS analysis. M.F., P.W., and A.E.B. developed the experimental elastoresistance setup. M.F. performed the elastoresistance experiments and analyzed the data. C.M. realized the thermal expansion measurements. K.W. performed the specific heat measurements. T.L., S.M.S., and M.M. performed the X-ray diffraction experiments. M.F., C.M., and A.E.B. developed the interpretations. M.F. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frachet, M., Wiecki, P., Lacmann, T. et al. Elastoresistivity in the incommensurate charge density wave phase of BaNi2(As1−xPx)2. npj Quantum Mater. 7, 115 (2022). https://doi.org/10.1038/s41535-022-00525-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-022-00525-8
This article is cited by
-
Charge density waves tuned by biaxial tensile stress
Nature Communications (2024)
-
Endotaxial stabilization of 2D charge density waves with long-range order
Nature Communications (2024)
-
An electronic nematic liquid in BaNi2As2
Nature Communications (2022)