Introduction

Sr2RuO4 is widely recognized as the paradigmatic example of a very clean, strongly correlated Fermi liquid (FL) with a simple quasi-two-dimensional Fermi surface (FS), from which an unconventional superconducting ground state emerges1,2. While the superconducting state has been a subject of intense study3,4,5, there are multiple attributes of Sr2RuO4 that motivate an in-depth analysis of the normal state, including the ability to characterize the FL state and quasiparticle dispersions with exquisite accuracy and the opportunity to study how the quasiparticles gradually lose coherence as temperature T is raised, evolving all the way into ‘bad metal’ behavior at high-T6,7,8.

Indeed, FL behavior applies only below a characteristic crossover temperature TFL ~ 30 K9 and is characterized, among other properties, by the expected thermal variation of the resistivity δρ ~ T2 and an enhanced T-independent Pauli susceptibility10,11. Interestingly, before settling into the Fermi-liquid temperature independent susceptibility, the NMR signal displays a shallow maximum at about 40 K11.

In the low-T FL regime, highly accurate determinations of the quasiparticle properties have been achieved using quantum oscillations (QO)12,13, angle-resolved photoemission spectroscopy (ARPES)14,15,16, and optical conductivity measurements17. The fermiology consists of three quasiparticle bands and associated FS sheets, conventionally labeled α, β, γ, forming predominantly from a hybridization of each of the Ru dxy, dzx,yz orbitals with oxygen 2p orbitals. Spin–orbit coupling (SOC) affects the orbital character of the quasiparticles states and leads to a high degree of orbital mixing for the β and γ branches along the Brillouin Zone diagonal16,18,19,20,21. The gradual breakdown of the quasiparticle picture at higher temperatures is revealed by transport measurements (resistivity)6 and Hall effect22,23,24, as well as ARPES and optical spectroscopy17.

The bands are strongly renormalized13 by electronic correlations. Theoretical work suggested7 that these correlations result from the combined effect of (i) the Hund’s rule coupling2,25, which has led to a characterization of Sr2RuO4 as a member of the broad family of ‘Hund’s metals’ and (ii) importantly, the proximity of the Fermi level to a van-Hove singularity (vHs) associated with the quasi-2D γ band8. The effects of passing EF through the vHs were experimentally studied with doping15, straining of thin films26 and application of uniaxial stress27,28. This last technique allows the effects of the vHs to be probed without introducing additional disorder. This was exploited also in a NMR study that revealed enhancements of the Knight shifts at the critical strain25. Theoretically, the study of the temperature dependence of the NMR response was reported7 for the unstrained case, but the detailed response of the Fermi-liquid correlations to applied stress is still an open question. The ARPES results reported in refs. 15,26 found no evidence for increased mass enhancement near the vHs in the former, and only a weak enhancement in the latter. On the other hand, a significant increase of the T2 coefficient associated with resistivity was reported under applied uniaxial stress27. This was later found to be consistent with a Boltzmann description of transport based on coherent quasiparticles close to a van-Hove singularity29,30.

Here we address the role of the vHs by acquiring 17O NMR data in the crucial temperature range around TFL ~ 30 K, under conditions of variable uniaxial stress. The results provide direct evidence that the crossover scale TFL is controlled by the location of the vHs relative to Fermi level EF, and moreover that the associated singular DOS strongly influences the physical properties such as spin susceptibility over an extraordinarily broad temperature range. TFL is driven to a vanishingly small value at the critical strain, and the spin susceptibility inferred from the 17O Knight shift measurements exhibits the expected logarithmic temperature dependence for a two-dimensional vHs. The non-FL magnetic response at the critical strain is marked by a strong nonlinear field dependence25, owing to comparable Zeeman and thermal energy scales, and a corresponding divergent singularity at the chemical potential. Our experimental results are shown to be in good agreement with a theoretical analysis based on a quasiparticle description starting from the band-structure evaluated under strain but keeping quasiparticle renormalizations independent on strain. This agreement hence provides further support for the limited role of strain on the quasiparticle renormalizations in this material.

Results

NMR experiments under uniaxial strain

To study the Fermi-liquid crossover upon approaching a van-Hove singularity, we performed 17O NMR experiments on Sr2RuO4 under in-plane uniaxial stress εaa in a temperature range 1.5–50 K at applied field strengths B = 3 T and 8 T. The magnetic field B∥b results in NMR intensity from three oxygen sites, labeled here as two in-plane sites O(1), O(\(1^{\prime}\)), and apical site O(2). For the O(1) site the neighboring Ru sites are along b direction, parallel to the magnetic field, hence the corresponding Knight shift is labeled K1∥ and for O(\(1^{\prime}\)), where the neighboring Ru sites are perpendicular to the magnetic field, the Knight shift is labeled as \({K}_{1^{\prime} \perp }\). (The in-plane site geometry is defined in the Supplementary Information.) Correspondingly, the hyperfine couplings are different, leading to distinct NMR absorption frequencies even in absence of strain. Taking into account also the electric quadrupolar coupling of the five I = 5/2 17O transitions, results in 15 total NMR absorption lines. In this work we focus on the NMR shift of the central transitions for the O(1) and O(1’) sites, which are rendered crystallographically inequivalent due to the B1g component of the strain. As such, the strain-dependent quadrupolar effects25 are subtracted out in the analysis, so as to isolate the hyperfine contribution to the total shift.

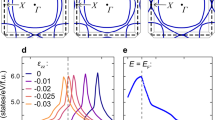
The measured shifts are shown in Fig. 1 where strain is seen to have a pronounced effect on the temperature dependence of the normal state behavior, and particularly so for the O(1) site. The applied stress for each measurement is referenced to the critical value εv corresponding to the Lifshitz transition. εv is determined empirically by tuning through a maximum in the shift magnitude concomitant with the transition25 (see Methods and Supplementary Information). In the unstrained case (black), an extremum is seen in the data at ~ 40 K followed by a crossover to the T-independent shift expected for a FL for temperatures T < TFL ~ 30 K11,31. TFL thus obtained is consistent with the FL crossover temperature observed by other methods1. The crossover temperature is observed to shift to lower value upon application of the a-axis stress (εaa = 0.65εv, red). At the critical strain (εaa = εv, green), TFL → 0. Additionally, at sufficiently low temperature the magnetic response is distinctly nonlinear at εv, shown in the inset of Fig. 1.

Fig. 1: Temperature-dependent 17O NMR Knight shifts, for different fields and strains.
figure 1

17O shift measurements recorded under zero strain, critical strain, and an intermediate strain are shown in the main panel. Note that for the critical strain, the effects of the singularity are more substantial in K1∥ than in \({K}_{1^{\prime} \perp}\). Error bars are determined by the NMR linewidth. Inset: Shift vs field data from ref. 25. The shifts at the critical strain εv exhibit a strong field dependence, observable for sufficiently low temperatures, that is associated with the Zeeman split of the singularity.

Full size image

Both the strong temperature dependence of the Knight shift under unstrained conditions, and the striking low-temperature variations of the shifts, especially in K1∥ while subjected to strain can be interpreted in the band-structure framework in terms of proximity to the van-Hove singularity in the γ band. For strains lower than the critical one, the van-Hove singularity (as shown in Fig. 2) is located at positive energy EvHs. The non-monotonic dependence of the Knight shift emerges due to a thermal depopulation of states as temperature drops below EvHs. Under strained conditions, the Fermi level moves toward the energy at the vHS, which explains both higher values of the Knight shift and the vanishing of the crossover scale.

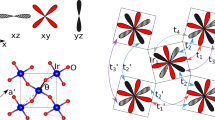
Fig. 2: Effect of strain and spin–orbit coupling on the quasiparticle density of states (QDOS).
figure 2

a The t2g (QDOS) as defined in the text. The main panel displays the region around EF while illustrating the influence of the spin–orbit coupling on the location of the van-Hove singularity. The inset shows the QDOS in a broader energy window. The Fermi surface is also shown (right inset). b Decomposition of the QDOS into contributions from the xy, zx, yz orbitals, at the critical strain at which the Fermi energy coincides with the van-Hove singularity. The inset displays the corresponding Fermi surface.

Full size image

Theoretical modeling of quasiparticle response

To make this discussion more quantitative, we consider a simple theoretical modeling in terms of quasiparticles. We introduce the quasiparticle Hamiltonian: \({\hat{H}}_{0}^{{{{\rm{qp}}}}}\,=\,\sqrt{\hat{Z}}\,{\hat{H}}_{{{{\rm{KS}}}}}\,\sqrt{\hat{Z}}\). In this expression, \({\hat{H}}_{{{{\rm{KS}}}}}\) is the Hamiltonian of Kohn–Sham states obtained from density-functional theory (DFT) (we use the generalized gradient approximation), and \(\hat{Z}\) is a matrix of quasiparticle weights, which reflect the correlation-induced renormalizations relating physical electrons to low-energy quasiparticles. We construct \({\hat{H}}_{{{{\rm{KS}}}}}\) by performing DFT calculations for a set of strains between 0.0% and 0.8%. We apply strain in the 〈100〉 direction and scale the 〈010〉 and 〈001〉 direction according to the experimentally determined Poisson ratios, − εyy/εxx = 0.508 and − εzz/εxx = 0.16332. We consider a minimal set of three low-energy bands, construct maximally localized Wannier functions33,34 of t2g symmetry and express \({\hat{H}}_{{{{\rm{KS}}}}}\) in this minimal basis set of localized orbitals. The matrix of quasiparticle weights \(\hat{Z}\) is diagonal in this localized basis and we use Zxy = 0.166 and Zxz/yz = 0.275 for T ≤ 30 K. These values are the renormalizations found from DMFT calculations in the Fermi-liquid regime of the unstrained material8, which are consistent with the mass enhancements obtained from ARPES16, optical spectroscopy17 and quantum oscillations experiments35. We also take into account that, above ~ 30 K, the renormalization is gradually reduced as temperature is increased, using Z(T) obtained in ref. 8.

Spin–orbit coupling (SOC) plays a key role in the physics of Sr2RuO4 . As in refs. 16,20,21,36,37, we take SOC into account in \({\hat{H}}_{{{{\rm{KS}}}}}\) as a local atomic term in the t2g basis. The bare DFT value of the SOC is about 0.1 eV. However, it is established from both theoretical calculations and experiments16,20,21,36 that electronic correlations lead to an effective enhancement of the SOC to roughly 0.2 eV. The quasiparticle density of states (QDOS) associated with \({\hat{H}}_{0}^{{{{\rm{qp}}}}}\) for unstrained Sr2RuO4 for 0.0, 0.1, and 0.2 eV SOC is shown in Fig. 2a. We see that including the (enhanced) SOC moves the vHs closer to the Fermi level. As a consequence, the critical strain corresponding to the Lifshitz transition is strongly reduced, an observation also made in refs. 25,32. By taking the enhancement of the SOC into account, we find a critical strain εaa ~ –0.5%, as shown in Fig. 2b, which is in good agreement with the experimental value of –0.44 ± 0.06%32. We note that by taking only the bare SOC into account, the critical strain is nearly a factor of two too large.

We calculate the magnetic susceptibility χqp(T) associated with the non-interacting quasiparticle Hamiltonian \({\hat{H}}_{0}^{{{{\rm{qp}}}}}\) by adding a magnetic field term and placing ourselves in the linear response regime (for details, see Methods). Orbitally resolved results are displayed in Fig. 3, as a function of temperature and for several values of the strain. The xz, yz component has a weak temperature and strain dependence, corresponding to a featureless shape of the density-of-states for that orbital. In contrast, \({\chi }_{xy}^{{{{\rm{qp}}}}}\) depends strongly on temperature and strain, due to the proximity to a 2D van-Hove singularity, resembling the behavior observed for the Knight shifts. For all values of the strain except the critical one, \({\chi }_{xy}^{{{{\rm{qp}}}}}\) displays a temperature-independent (Pauli) plateau at low-T. The temperature below which the plateau behavior is found decreases as strain is increased, and vanishes at the critical strain. On warming to temperatures T > TFL, the susceptibility first increases, as expected from the fact that a large density of states is thermally accessible close to the vHs, and then decreases on further warming. Secondary to the effect of the vHs, the temperature-dependent quasiparticle renormalization also contributes to the decrease in χqp above 30 K, as shown explicitly in the Supplementary Information.

Fig. 3: Comparison between calculated and measured susceptibility.
figure 3

a Susceptibility evaluated from the quasiparticle Hamiltonian as a function of temperature and a-axis strain, χqp(εaa, T). The susceptibility is resolved into contributions from the three t2g orbitals. The critical (compressive) strain is close to εaa = − 0.50%. b Experimentally determined \({K}_{1^{\prime} \perp }^{{{{\rm{s}}}}}-{K}_{1| | }^{{{{\rm{s}}}}}\) as a function of temperature and applied stress, referenced to the critical stress εv. Ks denotes the spin part of the total shift. To calculate the difference continuously, shifts have been interpolated from Fig. 1 after subtraction of the known orbital contribution. (\({K}_{1| | }^{{{{\rm{o}}}}}=+0.18 \%\), \({K}_{1{\prime} \perp }^{{{{\rm{o}}}}}=0.0 \%\))40. Error bars are determined by the average linewidth of the two sites. The inset on the right illustrates the Fermi-liquid crossover temperature as a function of uniaxial strain, extracted from our Knight-shift data. The defining criterion is the shift extremum separating the regimes of T-independent behavior, and that of logarithmic T-dependence. Error bars denote the temperature range in which the shift variation about the extremum is less than the linewidth.

Full size image

It is instructive to place our simple description in the broader context of a Landau theory of the Fermi-liquid state. In such a theory, quasiparticles interact and the magnetic susceptibility (in a simple single-band framework) is given by: \(\chi ={\chi }_{0}\frac{{m}^{* }/m}{1+{F}_{0}^{a}}\) where m*/m is the quasiparticle mass renormalization, \({F}_{0}^{a}\) is a Landau interaction parameter and χ0 is the bare susceptibility in the absence of any renormalizations. Our simple model only takes into account the \({\chi }_{0}\frac{{m}^{* }}{m}\) part of this expression (note that within a local description of the Fermi-liquid state m*/m = 1/Z). In other words, we assume that the dominant action is in the change in quasiparticle dispersions (fermiology of the system) as strain is applied, and not in the strain dependence of the Landau interaction parameters, which we assume to be weak. We also neglected the possible strain-dependence of the effective mass enhancements \(\hat{Z}\). Our working assumption of strain independent renormalizations is supported by good agreement with the experimental data presented here, but should be further quantified by other means, such as measurements of specific heat38 or high-resolution angular-resolved photoemission experiments. It should also be addressed by more elaborate computational approaches, such as dynamical mean-field theory, when the methods will allow for reliable solutions in the presence of spin–orbit coupling and low temperatures <10 K—for recent progress in this direction, see refs. 36,39.

Discussion

In order to make a semi-quantitative comparison of the calculations to the experiment it is convenient to take linear combinations of the measured Knight shifts to extract the orbital contributions to the susceptibility11. Indeed, the measured 17O Knight shifts in Fig. 1 include contributions from the spin responses associated with each of the three Fermi surfaces, as well as orbital contributions. Previous 17O NMR work40 determined the orbital shift for the two sites to be \({K}_{1| | }^{{{{\rm{o}}}}}=+0.18 \%\), \({K}_{1^{\prime} \perp }^{{{{\rm{o}}}}}=0.0 \%\); both values are consistent with recent examinations of the superconducting state41,42. Subtracting these terms from the total shifts shown in Fig. 1 leaves behind the contributions proportional to the electronic spin response Ks. The remaining 17O shift contributions are known to arise mostly from dipolar coupling to the occupied p-orbitals11,43. The tetragonal geometry then implies a coupling to the magnetization of the in-plane p-orbital for the O(\(1^{\prime}\)) site that is twice as large and with opposite sign to that of the O(1), while the couplings to the out-of-plane orbitals dominating the α, β bands are equivalent. As such, subtracting the shifts of both sites, as shown in the main panel of Fig. 3b, eliminates the shared contribution from the dxz/yz bands. Hence this quantity is, to first approximation, proportional to the dxy susceptibility. (The inset removes the factor 2 weighting for the O(\(1^{\prime}\)) shift and is representative of the average over the γ-band states within T of μ. Such a linear combination does not fully eliminate the contribution from xz/yz states, but due to the weak temperature and strain dependence of χxz/yz this contribution is just an approximately constant offset).

It should be noted, however, that under strained conditions the in-plane oxygen px and py orbitals are no longer equivalent, which complicates the analysis. The effects of the asymmetry are amplified by the relative sensitivities of the O(1), O(\(1^{\prime}\)) sites to the singularity at Y. Namely, the momentum-dependent overlap ∣bk∣ of oxygen 2p states with the hybridized γ-band wave functions is far greater for the O(1) site, than for the O(\(1^{\prime}\)) site for momenta near Y25. We discuss further this effect in the Supplementary Information.

So, how do the calculated χxy and the difference between the two oxygen shifts compare? At zero strain (black points), there is good semi-quantitative agreement. At εaa = 0.65 εv (red), and εaa = εv (green), the calculated susceptibility has the same qualitative behavior as the measured \({K}_{1^{\prime} \perp }^{s}-{K}_{1| | }^{s}\). As strain is increased, the FL coherence temperature is driven to zero TFL → 0 and Eγ(Y) → 0 (ε → εv). Furthermore, the agreement between the low-temperature strain enhancement of the susceptibility is also reasonable, with about 23% enhancement observed in \({K}_{1^{\prime} \perp }^{s}-{K}_{1| | }^{s}\) compared to 17% in the calculated \({\chi }_{xy}^{{{{\rm{qp}}}}}\) at 4 K. The calculated unstrained FL crossover temperature in Fig. 3a is slightly lower than that seen in the measured shifts (about 20 K, or reduced by half relative to the maximum at 40 K, see the right inset of Fig. 3b, a discrepancy that can be explained by the underestimation of EF − EvHs ≃ 7 meV inherent to the calculation (experiments suggest EF − EvHs ≃ 10–14 meV)15. As such, the ability of the quasiparticle framework described in this work to reproduce the salient behavior observed in the measured 17O Knight shifts provides strong support for the interpretation that the Fermi-liquid crossover, as well as the approximately logarithmic T-dependence for T > TFL, is a consequence of the close proximity of EF to a (quasi-)2D singularity in the DOS. Interestingly, judging from the agreement, the quasiparticle renormalizations do not substantially increase under strain, at least in the studied temperature range. For a system at the actual 2D singularity one could expect the mass enhancement to also exhibit a logarithmic growth upon lowering T. Whether this growth simply occurs with a small prefactor and hence quantitatively the effects are small down to 2 K, or, alternatively, other effects such as small but finite warping of the Fermi surfaces in the z direction could also play a role remains to be investigated in future work.

In considering the implications for the superconducting ground state, it is natural to expect that the strain response of Tc might similarly be dominated by the QDOS enhancement. For example, in a BCS weak coupling theory we have \({T}_{{{{\rm{c}}}}}=\omega {e}^{-1/{N}_{{{{\rm{qp}}}}}V}\), with the coupling constant V and Nqp the QDOS. Using the results calculated here, δNqp/Nqp ≃ 15%, leads to δTc/Tc = 2.5 (an unusual feature of the present case is that the strongly field-dependent shifts at the critical strain imply that the QDOS varies substantially over the gap scale). Note that, by symmetry, the gap vanishes at Y for any odd parity order parameter, hence the above scenario is consistent with the prior evidence for even parity superconductivity from Knight shift measurements41,42.

We emphasize that, in order to keep our theoretical description simple, we did not consider two possible effects, which should be addressed in future work. The first is a possible strain-dependence of the quasiparticle mass enhancements, and the second is the strain-dependence of the Stoner enhancement factor \(1/(1+{F}_{0}^{a})\). However, the striking agreement with experiment found here, neglecting these effects, suggests they are not crucial to understanding the Fermi-liquid behavior near the Lifshitz transition. We note however that an increase of the Stoner factor under strain was found in a previous density-functional theory calculation25. Another interesting issue is the departure from Fermi-liquid theory at the critical strain25,30. In tetragonal Sr2RuO4, the quasiparticle coherence is well-known to be resilient to temperatures exceeding the nominal TFL6,17,22,23,24, and we also note that measurements of the temperature-dependent bulk DC susceptibility (detailed in the Supplementary Information) are consistent with that of the NMR shifts even up to 300 K. These observations support the use of a quasiparticle framework to describe the strained material as done here, but a full DMFT calculation performed under strain and at low temperature would be an important check on this approach.

To summarize, the normal state transition from an incoherent-like regime to a Fermi-liquid-like regime in Sr2RuO4 is shown tunable by the application of in-plane strain. The crossover temperature is driven to lower values as the critical strain is approached, as shown in the right inset of Fig. 3b, corresponding to the Lifshitz transition for Sr2RuO4. Near to the critical strain, the quasiparticle description remains valid, and the increased density of states inferred from the NMR shift enhancements appears qualitatively consistent with the increase in superconducting transition temperature. The results imply that the proximity to the van-Hove singularity is a dominant factor for the macroscopic normal state properties over a broad temperature range. In the unstrained material, this framework naturally accounts for the temperature variation of the susceptibility for T > TFL, which was previously not well understood. In spite of the strong effect of the van-Hove singularity on the crossover temperature, which is consistent with what is found in transport29,32, the effects of the strain on the quasiparticle renormalization are found to be limited. In comparison to earlier work on doped samples or films15,26 the level of disorder is smaller and the singularity correspondingly sharper: the insensitivity of renormalizations to strain is a surprising result that motivates further development of DMFT methods capable of reaching lower temperatures and with higher energy resolution.

Methods

Experimental details

An 17O enriched single crystal of Sr2RuO4 with dimensions 3.0 × 0.4 × 0.2 mm was mounted onto a piezo-electric variable stress/strain device (www.razorbillinstruments.com/sdm_downloads/cs120-datasheet) such that the applied uniaxial stress was aligned with the crystallographic a-axis. In this device, the rectangular bar is clamped on two ends, such that the strained portion of approximately 1 mm length forms the bridge between the clamps. The subsequently wound inductive coil and resonant tank circuit (10–50 MHz) was configured for top-tuning/matching, such that the stress axis coincides with the coil symmetry axis, and the field orientation B0∥b when placed in the variable temperature cryostat. Compressive stress was applied to the sample in-situ via an external voltage to the piezo-electric stacks of the strain device. The NMR frequencies of the 17O central transitions (−1/2 ↔ +1/2) were measured at applied field strengths B = 3T, 8T, strains (εaa = 0, εaa = 0.65εv, εaa = εv), and covering temperatures T = 1.5 − 50 K. For the O(\(1^{\prime}\)) site there is a discrepancy between the absolute values of the unstrained shift reported in ref. 11 compared to those of refs. 43,25, and the current work. However, the temperature-dependent changes, which are of interest here are consistent throughout. As such, to compare appropriately a constant offset of −0.055% was added to the \({K}_{1^{\prime} \perp }\) data of ref. 11 plotted in Fig. 1 and Fig. 3.

Throughout, the strains are referenced to the critical compressive strain at the Lifshitz transition, which was identified empirically by tuning through an extremum in the NMR shifts; these measurements are detailed in the Supplementary Information. The critical strain was estimated in a previous NMR work25 to be εaa ≃ − 0.59%, using a capacitive sensor to measure the relative distance changes between the sample clamps in the strain device. The displacements measured by this method overestimate the actual compressive strain, because it does not take into account deformations of the epoxy and the strain device. A corrected value for the critical a-axis strain (εaa = − 0.44%) was first obtained in ref. 32 by incorporating a force sensor into the device, and taking into account the low-temperature elastic moduli obtained from Resonant Ultrasound Spectroscopy measurements.

Computational details

We use the experimental lattice parameters a = b = 3.8613 Å, c = 12.7218 Å from ref. 44 measured at 8 K. The internal coordinates (apical O and Sr z-position) of the unstrained structure were relaxed within DFT resulting in zO = 0.16344 and zSr = 0.35230 (compared to the experimental ones of: 0.1634(4) and 0.3529(4)). For simplicity, we do not optimize the internal coordinates under strain. We confirmed with calculations at higher strains that the internal coordinates are not affected much by the applied strain. The DFT calculations have been performed with WIEN2k45 within the generalized gradient approximation46, using RKmax = 8 and a shifted 27 × 27 × 27 k-grid.

For the Wannier construction we use wien2wannier47 and Wannier9048, a 10 × 10 × 10 k-grid and a frozen energy window ranging from –1.77 to 3 eV for all strains.

For the calculation of the susceptibility we evaluate the up/down spin DOS under an applied magnetic field of 2 T on a very dense 3360 × 3360 × 3360 k-grid and an energy grid with a spacing of 0.28 meV.

Parts of the calculations have been performed using the TRIQS library49.