Abstract
Prototypical models and their material incarnations are cornerstones to the understanding of quantum magnetism. Here we show theoretically that the recently synthesized magnetic compound Na2BaCo(PO4)2 (NBCP) is a rare, nearly ideal material realization of the S = 1/2 triangular-lattice antiferromagnet with significant easy-axis spin exchange anisotropy. By combining the automatic parameter searching and tensor-network simulations, we establish a microscopic model description of this material with realistic model parameters, which can not only fit well the experimental thermodynamic data but also reproduce the measured magnetization curves without further adjustment of parameters. According to the established model, the NBCP hosts a spin supersolid state that breaks both the lattice translation symmetry and the spin rotational symmetry. Such a state is a spin analog of the long-sought supersolid state, thought to exist in solid Helium and optical lattice systems, and share similar traits. The NBCP therefore represents an ideal material-based platform to explore the physics of supersolidity as well as its quantum and thermal melting.
Similar content being viewed by others
Introduction
Quantum magnets are fertile ground for unconventional quantum phases and phase transitions. A prominent example is the S = 1/2 triangular-lattice antiferromagnet (TLAF). Crucial to the conception of the quantum spin-liquid state1, its inherent geometric frustration and strong quantum fluctuations give rise to exceedingly rich physics. In the presence of an external magnetic field, spin anisotropy, and/or spatial anisotropy, the system exhibits a cornucopia of magnetic orders and phase transitions2,3,4. In particular, introducing an easy-axis spin exchange anisotropy to the TLAF results in the spin supersolid5,6,7,8,9,10,11 in zero magnetic field. Applying a magnetic field along the easy-axis drives the system through a sequence of quantum phase transitions by which the spin supersolidity disappears and then reemerges12, whereas applying the field in the perpendicular direction yields distinct, even richer behaviors13. The S = 1/2 easy-axis TLAF therefore constitutes a special platform for exploring intriguing quantum phases and quantum phase transitions.
Lately, a cobalt-based compound Na2BaCo(PO4)2 (NBCP) has been brought to light14,15,16,17. This material features an ideal triangular lattice of Co2+ ions, each carrying an effective S = 1/2 spin owing to the crystal field environment and the significant spin-orbital coupling17,18 (Fig. 1a). Early thermodynamic measurements show that NBCP does not order down to ~300 mK with a large magnetic entropy (~2 J mol−1 K−1) hidden below that temperature scale14. A later thermodynamic measurement reveals a specific heat peak at ~150 mK, which accounts for the missing entropy and points to a possible magnetic ordering in zero magnetic field15. However, the muon spin resonance (μSR) experiment finds strong dynamical fluctuation down to 80 mK16 which may suggest a spin-liquid like state. The multitude of experimental results call for a theoretical assessment.
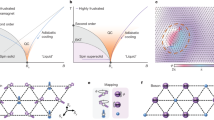
a Top view of the crystallographic structure of the NBCP. Each Co2+ ion carries an effective S = 1/2 spin owing to the octahedral crystal environment and the spin-orbital coupling. The spins form a triangular network. Its magnetic ground state is a spin supersolid: the red (blue) circles represent the positive (negative) Sz component, and the black arrows show the direction of the Sx,y component. The crystallographic a-, b-, and c-axes and the spin frame Sx,y,z are shown in the bottom right and the top left insets, respectively. b Shows the projection of the fitting loss function onto the Jxy – Jz plane (with JPD,Γ fixed as zero), where brighter color represents less fitting loss and therefore better fit. The white cross marks the optimal parameter set, which corresponds to an S = 1/2 TLAF with anisotropy parameter Δ = Jz/Jxy ≃ 1.7 (dashed line).
Previous works have attempted at establishing the spin exchange interactions in this compound. The authors in ref. 15 suggest an exchange coupling ~2 K based on an analysis of the magnetic susceptibility data, which is an order of magnitude smaller than an earlier estimate of 21.4 K in ref. 14. Meanwhile, a first-principle calculation suggests potentially significant Kitaev-type exchange interaction17. Despite these efforts, the precise spin Hamiltonian, its magnetic ground states, as well as the connection to experimental data, are yet to be established.
In this work, we show theoretically that NBCP can be well-described by a S = 1/2 easy-axis TLAF with negligible perturbations. We establish the microscopic description of NBCP with realistic model parameters by fitting the model to intermediate- and high-temperature experimental thermal data. We expedite the fitting process by using the Bayesian optimization19 equipped with an efficient quantum many-body thermodynamic solver—exponential tensor renormalization group (XTRG)20,21. Our model is corroborated by reproducing quantitatively the experimental low-temperature magnetization curves by density matrix renormalization group (DMRG)22 calculations. Furthermore, we are able to put the various experimental results into a coherent picture and connect them to the physics of the spin supersolid state. Therefore, the NBCP represents a rare material realization of this prototypical model system and thereby the spin supersolidity. The small exchange energy scale in this material (~1 K) implies that the phases of the NBCP can be readily tuned by weak or moderate magnetic fields. Our results also highlight the strength of the many-body computation-based, experimental data-driven approach as a methodology for studying quantum magnets.
Results
Crystal symmetry and the spin-1/2 model
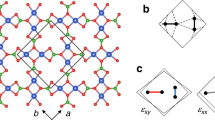
Figure 1a shows the lattice structure of NBCP and the crystallographic a-, b-, and c-axes. Due to the octahedral crystal field environment and the spin-orbital coupling, each Co2+ ion forms an effective S = 1/2 doublet in the ground state, which is separated from higher energy multiplets by a gap of ~71 meV (see Supplementary Note 1). Super-super-exchange path through two intermediate oxygen ions produces exchange interactions between two nearest-neighbor (NN) spins, thereby connecting them into a triangular network (see density functional theory calculations in the Supplementary Note 2). Further-neighbor spin exchange interactions are suppressed by the long distance. Meanwhile, the inter-layer exchange interactions are expected to be much smaller than the intra-layer couplings owing to the non-magnetic BaO layer separating the adjacent cobalt layers. Therefore, we model the NBCP in the experimentally relevant temperature window as a S = 1/2 TLAF with dominant NN exchange interactions. This hypothesis will be justified a posteriori.
The crystal symmetry constrains the NN exchange interactions as follows23. The threefold symmetry axis ∥c passing through each lattice site relates the exchange interactions on the 6 bonds emanating from that site. On a given bond, there is a twofold symmetry axis passing through that bond and a center of inversion. The former symmetry forbids certain components of the off-diagonal symmetric exchange interaction, whereas the latter forbids Dzyaloshinskii-Moriya interactions. We obtain
with
where i, j are a pair of neighboring lattice sites, and α, β label the spin x, y, z components24,25,26. We choose the spin frame such that x∥a, z∥c. \(\varphi \,=\,\{0,\frac{2\pi }{3},-\frac{2\pi }{3}\}\) for three different types of NN bonds parallel to a, b, and −(a + b), respectively. Jxy, Jz, JΓ, and JPD are respectively the XY, Ising, off-diagonal symmetric, and pseudo-dipolar exchange couplings (see more details in Supplementary Note 3). The entire model parameter space is thus spanned by the four exchange constants, two Landé factors (gab and gc, for perpendicular and parallel to the c-axis, respectively), as well as two van Vleck paramagnetic susceptibilities (\({\chi }_{ab}^{{{{\rm{vv}}}}},{\chi }_{c}^{{{{\rm{vv}}}}}\)), all of which are taken to be constants in the experimentally relevant temperature/magnetic field window.
Determination of the model parameters
We determine the model parameters in Eq. (1) by fitting the experimental magnetic specific heat (Cm) and magnetic susceptibility (χ) data at temperature T ≥ Tcut, where Tcut = 1 K for Cm and 3 K for χ. Note the magnetic susceptibilities are remeasured in this work with high quality samples. For each trial parameter set, we compute the same thermodynamic quantities from the model by using the XTRG solver21,27. We search for the parameter set that minimizes the total loss function through an unbiased and efficient Bayesian optimization process19. See Methods for more details.
We set the cutoff temperature Tcut based on the following considerations. The experimental data from independent measurements agree with each other at T > Tcut, and our XTRG solver does not exhibit significant finite-size effects above Tcut. Meanwhile, the Tcut has to be less than or comparable with the characteristic energy scale of the material. These constraints fix Tcut to our present choices.
The searching process yields the following optimal parameter set: Jxy = 0.88 K, Jz = 1.48 K, and JΓ,PD are negligible. The Landé factors gab = 4.24, and gc = 4.89. The van Vleck susceptibilities \({\chi }_{ab}^{{{{\rm{vv}}}}}\,=\,0.149\) cm3 mol−1 and \({\chi }_{c}^{{{{\rm{vv}}}}}\,=\,0.186\) cm3 mol−1. To ensure that the algorithm does converge to the global minimum, we project the loss function onto the (Jxy, Jz) plane in Fig. 1b, where, for fixing values of Jxy, Jz, the loss function is minimized over the remaining parameters. The fitting landscape reveals a single minimum. The estimated value of exchange parameters and their bounds of uncertainty are shown in Fig. 2f.
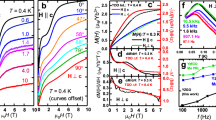
a Shows the magnetic specific heat Cm of the NBCP as a function of temperature T, reported by two independent measurements (Zhong et al.14 and Li et al.15) as well as the best fit. The gray dashed line marks Tcut. The XTRG fitting is performed for experimental data at T > Tcut. b, c Show respectively parallel and perpendicular to the c-axis magnetic susceptibilities with the experimental data measured in this work (see Methods) and the best fit. d, e Show the magnetization as a function of the magnetic field in the c and a directions, respectively. The experimental data were obtained from Li et al.15 with the van Vleck paramagnetic contributions subtracted off. The model prediction is obtained from DMRG, which agrees quantitatively with experiment. The gray lines show magnetization curves obtained from models with various anisotropy parameters Δ, with Jxy tuned to the optimal value. f Shows the standard box plot of the optimal parameters, with the red line indicating the median value, the top(bottom) edge of the box representing the upper(lower) quartile of the best 20 model parameter sets found in 450 Bayesian optimization runs.
The small uncertainties in Jxy and Jz, as well as the small loss, indicate that the experimental data are well captured by our parameters. Indeed, Fig. 2a–c show respectively the specific heat and the magnetic susceptibility as functions of temperature. We find excellent agreement between the model calculations and the experiments within the fitting temperature range T ≥ Tcut. Reassuringly, the Landé factors obtained by us are in excellent agreement with the latest electron-spin resonance measurement (gab = 4.24 and gc = 4.83)17. We have also calculated the magnetic specific heat Cm in non-zero magnetic fields and find good agreement with the experiments whenever the two independent measurements14,15 mutually agree (Supplementary Note 4). Note in Fig. 2a the two experimental data sets of specific heat differ at T < Tcut. Our model’s behavior below Tcut is in agreement with one of them. The discrepancy in the experimental data calls for further investigation.
Our model parameters pinpoint to an almost ideal S = 1/2 TLAF with significant easy-axis anisotropy Δ = Jz/Jxy ≈ 1.68. In particular, the negligible off-diagonal exchange interactions imply that the NBCP features an approximate U(1) spin rotational symmetry with respect to c axis. As a result, the magnetization curve with field B∥c in Fig. 2d has a couple of idiosyncratic features: It shows a 1/3-magnetization plateau in an intermediate field range [Bc1, Bc2], and another fully magnetized plateau above the saturation field Bc3. As an independent estimate of Δ, we note the semi-classical analysis shows that \({B}_{c2}/{B}_{c1}\,=\,{{\Delta }}\,-\,1/2\,+\,\sqrt{{{{\Delta }}}^{2}\,+\,{{\Delta }}\,-\,7/4}\) and Bc3/Bc1 = 2Δ + 1 (Supplementary Note 5). Using the experimental values Bc1 ≈ 0.35 T and Bc3 ≈ 1.62 T15, we estimate Δ ≈ 1.81, which is consistent with the Bayesian search result. Meanwhile, using these numbers, we can estimate Bc2 ≈ 1.10 T, which is fairly close to the experimental value of 1.16 T15.
As a corroboration of our model, we perform DMRG calculations of the zero-temperature magnetization curves and find quantitative agreement with the experimental results (Fig. 2d, e). With no further adjustment of the parameters, the model can not only produce the correct transition fields but also the details of the magnetization curve between the transitions. We find that the magnetization curve ∥c is a sensitive diagnostic for the anisotropy parameter Δ. The agreement between the model and the experiments is quickly lost when Δ deviates slightly from the optimal value in Fig. 2d.
Taken together, the broad agreements between the semi-classical estimates, the quantum many-body calculations, and experimental data strongly support the S = 1/2 easy-axis TLAF as an effective model description for the NBCP.
Field-tuning of the spin supersolid state
The S = 1/2 easy-axis TLAF exhibits a sequence of magnetic phases and quantum phase transitions driven by magnetic fields12,28,29. The experimentally measured differential susceptibilities (dM/dB) show a few anomalies when the field is ∥c and ∥a and are attributed to quantum phase transitions15. Here, we clarify the nature of the magnetic orders of NBCP based on the S = 1/2 easy-axis TLAF model.
Figure 3a shows the theoretical zero-temperature phase diagram of our model in field ∥c, obtained from DMRG calculations. The system goes through successively the Y, Up-Up-Down (UUD), V, and the polarized (Pz) phases with increasing field. These phases are separated by three critical fields Bc1,c2,c3 = 0.36 T, 1.14 T, 1.71 T discussed in the previous section, which are manifested as peaks in dM/dB. The Y phase, as well as the V phase, spontaneously break both the lattice translation symmetry and the U(1) symmetry, thereby constituting the supersolid state analogous to that of the Bose atoms. The UUD phase, on the other hand, restores the U(1) symmetry but breaks the lattice translation symmetry. This state is analogous to a Bose Mott insulator state. The magnetic plateau associated with the UUD state reflects the incompressibility of the Mott insulator.
a Shows the entanglement entropy and differential magnetic susceptibility dM/dB as functions of field B in the c direction. The Y, UUD, V, and Pz phases are shaded in different colors. Bc1,c2,c3 are the three critical fields separating these phases. The corresponding spin configurations are also shown. Red (blue) circles represent the positive (negative) Sz component. Black arrows show the direction of the in-plane (Sx,y) component. b Is similar to (a) but for field B∥a. The λ phase, \(\widetilde{{{{\rm{Y}}}}}\) phase, \(\tilde{{{{\rm{V}}}}}\) phase, and Px phase are separated by three critical fields Ba1,a2,a3. c Is a zoom-in of (b), showing the side view of the spin configurations, as well as the evolution of the order parameter Θ as a function of the field (see main text for definition).
The situation is yet more intricate when the field ∥a. DMRG calculations show that the system goes through the λ, \(\tilde{{{{\rm{Y}}}}}\), \(\tilde{{{{\rm{V}}}}}\) (see Fig. 3c for an illustration), and the quasi-polarized Px phases, which are separated by three critical fields Ba1 = 0.075 T, Ba2 = 0.75 T, and Ba3 = 1.51 T. The presence of a field ∥a breaks the U(1)-rotational symmetry with respect to the Sz axis but preserves the π-rotational (Z2) symmetry with respect to the Sx axis. The λ phase, where the spins sitting on three magnetic sublattices form the greek letter “λ”, spontaneously breaks both the Z2 symmetry and the lattice translation symmetry. The Z2 symmetry is restored in the \(\tilde{{{{\rm{Y}}}}}\) phase, and spontaneously broken again in the \(\tilde{{{{\rm{V}}}}}\) phase.
Comparing to the field-induced transitions in B∥c case, the transitions at Ba1,a2 show much weaker anomalies in dM/dB when B∥a. Numerically, we detect these two transitions using an order parameter \({{\Theta }}\,=\,\frac{1}{\pi }| ({\theta }_{a}\,-\,{\theta }_{b}\,-\,{\theta }_{c})|\), where θa,b,c measure the angle between the spin moments on three sublattice and the Sx axis. Θ = 0 when the Z2 symmetry is respected and Θ ≠ 0 when it is broken. Figure 3c shows Θ as a function of field, from which we can delineate the boundaries between λ, \(\tilde{{{{\rm{Y}}}}}\), and \(\tilde{{{{\rm{V}}}}}\) phases, with the critical fields Ba1 ≈ 0.07 T and Ba2 ≈ 0.75 T. The small value of Ba1 implies it could be easily missed in experiments. Meanwhile, the weak anomalies in dM/dB associated with Ba1,a2 make them difficult to detect in thermodynamic measurements. We note that dM/dB shows a broad peak in the \(\tilde{{{{\rm{Y}}}}}\) phase at ~0.4–0.5 T15. This peak appears in the experimental data and was previously interpreted as a transition. The true transitions (Ba1,a2) are in fact above and/or below the said peak. We also note that, despite of the weak anomaly observed numerically at Ba2, the quantum phase transition there is likely of first-order from symmetry analysis: the \(\tilde{{{{\rm{Y}}}}}\) and \(\tilde{{{{\rm{V}}}}}\) phases both have a sixfold ground-state degeneracy and they have incompatible symmetry breaking; thus the transition cannot be continuous according to Landau’s paradigm.
Strong spin fluctuations and phase diagram at finite temperature
Having established the zero-temperature phase diagram of the NBCP, we now move on to its physics at finite temperature. Figure 4a shows the contour plot of Cm/T as a function of temperature and field B∥c. In the temperature window accessible to the XTRG, we find a broad peak near zero field, which moves to higher temperature and becomes sharper as field increases. These features are in qualitative agreement with the experimental findings.
a Shows Cm/T, calculated from XTRG, as a function of temperature T and magnetic field ∥c. The open squares mark the peaks of the experimental Cm/T data (Li et al.15). b Shows Cm/T under zero field, and the magnetic entropy Sm, as functions of temperature. The experimental Sm data are obtained by integrating numerically the Cm/T data. The experimental entropy curve is shifted by 0.55 Jmol−1K−1 to match the saturation value \(R\ln (2)\) at sufficiently high temperature. c Shows the temperature-field phase diagram constructed from the classical Monte Carlo (MC) simulation. The blue triangles mark the three-state Potts transitions determined by using the Binder cumulants. Red solid circles mark the BKT transitions determined from the spin stiffness (see Methods). The zero field BKT transition temperatures are reported by ref. 31. The red solid line along the vertical axis under zero field indicates the regime with algebraic spin correlation in the Sz spin component. d Shows the specific heat as a function of temperature for various representative magnetic field ∥c, obtained from the classical MC simulation.
Figure 4b shows a cross-section of the contour plot at zero field. The model produces a peak in Cm/T at ≈ 150 mK, which is in excellent agreement with the experimental data from ref. 15. Note this temperature is well below the temperature window (above Tcut) used for fitting, the difference between theory and experiment at very low temperatures may be ascribed to the finite-size effect inherent in the XTRG calculations (see Methods). The magnetic entropy also shows quantitative agreement with the experimental data. In particular, there is still a considerable amount of magnetic entropy to be released at 300 mK (and even down to 150 mK). The missing entropy at 300 mK reported in ref. 14 can be ascribed to the small spin interaction energy scale and high degrees of frustration in the NBCP.
To understand the finite-temperature phase diagram of the NBCP, we perform a Monte Carlo (MC) simulation of the classical TLAF model with appropriate rescaling of temperature and magnetic field30,31,32,33. This approximation is amount to neglecting fluctuations in the imaginary time direction in the coherent-state path integral of the S = 1/2 TLAF. As the finite-temperature phase transitions are driven by thermal fluctuations, we expect that the salient features produced by the classical MC simulations are robust. Meanwhile, the MC simulation allows for accessing much larger system sizes and lower temperatures comparing to the XTRG for quantum model simulations.
The physics of the classical TLAF model is well documented; here, we focus on the features that can be directly compared with available experimental data. Figure 4c shows the MC-constructed T-B phase diagram with B∥c. Figure 4d shows the specific heat as a function of temperature for various representative fields. The phase diagram shows a broad dome of UUD phase, beneath which lie the Y phase at low field and the V phase at high field. The UUD phase and the paramagnetic phase are separated by a transition of three-state Potts universality; the Y and V phases and the UUD phase are seperated by the Berezinskii-Kosterlitz-Thoueless (BKT) transitions. Note the MC simulation may seem to suggest the onset of the V phase precedes that of the UUD phase at high field; this is an finite-size effect. On symmetry ground, we expect that the onset of the UUD phase either precedes that of the V phase through two continuous transitions, or the system enters the V phase directly through a first-order transition.
At zero field, the specific heat shows two broad peaks, which are related to the two BKT transitions accompanying the onset of the algebraic long-range order in Sz and Sx components, respectively30,31. The experimentally observed specific heat peak ~150 mK may be related to the higher-temperature BKT transition; the lower-temperature BKT transition (around 54 mK as estimated by classical MC simulations) is yet to be detected as they lie below the temperature window probed by the previous experiments. The strong dynamical spin fluctuations found in μSR experiment at 80 mK is naturally attributed to the algebraic long-range order in the Sz component. Note there exists arguments for a third BKT transition32 although it is not observed in classical MC simulations31.
When the magnetic field is switched on, the specific heat shows a sharp peak signaling the three-state Potts transition from the high-temperature paramagnetic phase to the UUD phase, corresponding to onset of the long-range order in the Sz component. This is consistent with the experimentally observed sharp specific heat peak at finite fields15. At lower temperature, the specific heat shows a much weaker peak related to the BKT transition into either the Y phase or the V phase, corresponding to the onset of the algebraic long-range order in Sx. The lower-temperature BKT transitions are yet to be detected by experiments.
Discussion
The supersolid, a spatially ordered system that exhibits superfluid behavior, is a long-pursued quantum state of matter. The question of whether such a fascinating phase of matter exists in nature has spurred intense research activity, and the search for supersolidity has become a multidisciplinary endeavor34,35,36,37,38,39. The early claim of observation in He-434 turned out to be an experimental artifact35. Nevertheless, it has inspired new lines of research in ultracold quantum gases36,37,38,39. Meanwhile, it has been proposed theoretically that the ultracold Bose atoms in a triangular optical lattice can host a supersolid state5,6,7,8. Yet, the realization of such a proposal has not been reported up to date.
An equivalent, yet microscopically different route to the triangular-lattice supersolidity is via the easy-axis S = 1/2 TLAF magnet. The spin up/down state of a magnetic ion can be viewed as the occupied/empty state of the lattice site by a Bose atom, and the spin rotational symmetry with respect to the easy axis is mapped to the U(1) phase rotation symmetry. By virtue of this mapping, the spin ground state in the easy-axis TLAF, which spontaneously breaks both lattice translation symmetry and spin rotational symmetry, is equivalent to the supersolid state of Bose atoms.
Despite its simple setting, ideal S = 1/2 TLAF has rarely been found in real materials. Although TLAFs with higher spin (S > 1/2) are known3, S = 1/2 systems with equilateral triangular-lattice geometry, such as Ba3CoSb2O940,41,42,43,44,45,46,47 and Ba8CoNb6O2448,49, were synthesized and characterized not until recently. The former shows easy-plane anisotropy28,47, whereas the latter material is thought to be nearly spin isotropic48,49,50. To the best of our knowledge, ideal S = 1/2 easy-axis TLAFs are yet to be found. In this work, we show that the NBCP is an almost ideal material realization of such an S = 1/2 easy-axis TLAF with the anisotropy parameter Δ ≈ 1.7.
Our model arranges the various pieces of available experimental data into a coherent picture by connecting them to the rich physics of the TLAF model. It permits a quantitative fit of the thermodynamic data, including specific heat Cm and magnetic susceptibility χ down to intermediate and even low temperatures. In particular, we obtain the Cm/T peak at around 150 mK observed in experiments15, which we associate to the BKT transition. Furthermore, we are able to accurately reproduce the spin state transition fields observed in previous AC susceptibility measurements along both a and c axes and clarify their nature.
The obtained spin exchange interactions are on similar orders of magnitude as previous estimation based on the Curie-Weiss fitting of the magnetic susceptibility15 and first-principle calculation17. However, the first-principle calculation suggests a significant Kitaev-type exchange interaction (in a rotated spin frame)17, whereas our model, being directly fitted from the experimental data, possesses a nearly ideal U(1) symmetry and negligible Kitaev-type interaction (see more discussions in Supplementary Note 3). The nearly ideal U(1) symmetry in this material is indicated by the well-quantized magnetization plateau (Fig. 2d), which would be absent without the U(1) symmetry.
In our fitting procedure, we have omitted at the outset all further-neighbor exchange interactions on the ground that their magnitude must be suppressed by the large distance between further-neighbor Co2+ ions. This can be verified by including in the model a second-neighbor spin-isotropic exchange interaction J2. To verify it, we have performed additional 400 Bayesian iterations and find J2 with the median value ~0.1 K amongst the best 20 parameter sets, which are negligibly small. We thus conclude the obtained optimal parameters in the simulations are robust.
Despite the essential challenge in the first-principle calculations of the strongly correlated materials, we may nevertheless employ the density functional theory (DFT) + U approach to justify certain aspects of the microscopic spin model that are accessible to this approach. First of all, we find the charge density distributions of 3d electrons of Co2+ ions are well separated from one triangular plane to another (see Supplementary Note 2), which ensures two-dimensionality of the compound. Moreover, the in-plane charge density distribution reveals clearly a super-super-exchange path between the two NN Co2+ ions. We construct the Wannier functions of d-orbitals of Co2+ ions and extract the hopping amplitude t between two NN Co2+ ions. From the second-order perturbation theory in t/U, the NN exchange coupling can be estimated to be on the order of 2–3 K for moderate and typical Ueff = 4–6 eV in this Co-based compound17, which is consistent with the energy scales of the spin model.
The accurate model for the NBCP also points to future directions for the experimentalists to explore. The model hosts a very rich phase diagram in both temperature and magnetic field, which are yet to be fully uncovered by experiments. In particular, the model shows a second BKT transition at ~50 mK in zero field; in finite field B∥a, the model shows two subtle transitions at Ba1 ≈ 0.07 T and Ba2 ≈ 0.75 T. These transitions may be detected by nuclear magnetic resonance51, magneto-torque measurements52, and magnetocaloric measurements53,54,55. Neutron scattering experiments can also be employed to detect the simultaneous breaking of discrete lattice symmetry and spin U(1) rotational symmetry, as well as the behaviors of spin stiffness, so as to observe spin supersolidity in this triangular quantum magnet. On the theory front, while the S = 1/2 easy-axis TLAF and its classical counterpart share similar features in their finite-temperature phase diagrams, it was realized early on that the quantum model also possess peculiar traits that are not fully captured by the classical model32. Clarifying these subtleties in the context of NBCP would also presents an interesting problem for the future.
Methods
Exponential tensor renormalization group
The thermodynamic quantities including the magnetic specific heat Cm, and magnetic susceptibility χ can be computed with the exponential tensor renormalization group (XTRG) method21,27. In practice, we perform XTRG calculations on the Y-type cylinders with width W = 6 and length up to L = 9 (denoted as YC6 × 9, see Supplementary Note 4), and retain up to D = 400 states with truncation errors ϵ ≲ 1 × 10−4 (down to 1 K) and ≲1 × 10−3 (down to about 100 mK). The XTRG truncation provides faithful estimate of error in the computed free energy, and the small ϵ values thus guarantee high accuracy of computed thermal data down to low temperature.
The XTRG simulations start from the initial density matrix ρ0(τ) at a very high-temperature T ≡ 1/τ (with the inverse temperature τ ≪ 1), represented in a matrix product operator (MPO) form56. The series of density matrices ρn(2nτ) (n ≥ 1) at lower temperatures are obtained by iteratively multiplying and compressing the MPOs ρn = ρn − 1 ⋅ ρn − 1. As a powerful thermodynamic solver, XTRG has been successfully applied in solving triangular-lattice spin models50 and related compounds51,57, Kitaev model58 and materials59, correlated fermions in ultracold quantum gas60, and even moiré quantum materials61.
Automatic parameter searching
By combining the thermodynamic solver XTRG and efficient Bayesian optimization approach, the optimal model parameters can be determined automatically via minimizing the fitting loss function between the experimental and simulated data, i.e.,
\({O}_{\alpha }^{\exp }\) and \({O}_{\alpha }^{\mathrm{sim} ,{{{\bf{x}}}}}\) are respectively the experimental and simulated quantities with given model parameters \({{{\bf{x}}}}\,\equiv\, \{{J}_{xy},{J}_{z},{J}_{{{{\rm{PD}}}}},{J}_{{{\Gamma }}},{g}_{ab,c},{\chi }_{ab,c}^{{{{\rm{vv}}}}}\}\). The index α labels different physical quantities, e.g., magnetic specific heat and susceptibilities, and Nα counts the number of data points in Oα. The optimization of \({{{\mathcal{L}}}}\) over the parameter space spanned by {Jxy, Jz, JPD, JΓ} is conducted via the Bayesian optimization19. The Landé factor gab,c and the Van Vleck paramagnetic susceptibilities \({\chi }_{ab,c}^{{{{\rm{vv}}}}}\) are optimized via the Nelder-Mead algorithm for each fixing {Jxy, Jz, JPD, JΓ}. In practice, we perform the automatic parameter searching using the package QMagen developed by some of the authors19,62, and the results shown in the main text are obtained via over 450 Bayesian iterations. After that, we introduce an additional parameter, the next-nearest-neighbor Heisenberg term J2, and perform another 400 searching iterations. We find J2 is indeed negligibly small and the obtained optimal parameters are robust.
Density matrix renormalization group
The ground-state magnetization curves of the easy-axis TLAF model for NBCP are computed by the density matrix renormalization group (DMRG) method22, which is a powerful variational algorithm based on the matrix product state ansatz. The DMRG simulations are performed on YC6 × 15 lattice, and we retain bond dimension up to D = 1024 with truncation error ϵ < 3 × 10−5, which guarantees well converged DMRG data.
Classical Monte Carlo simulations
We replace the S = 1/2 operators by classical vectors, \({S}_{i}^{x,y,z}\,\to\, S{\hat{n}}_{i}\), where \({\hat{n}}_{i}\) is a unit vector, and S = 1/2 is the spin quantum number. We use the standard Metropolis algorithm with single spin update. The largest system size is 48 × 48. We compute the Binder ratio associated with the UUD-phase order parameter \(\psi \,=\,{m}_{1}\,+\,{m}_{2}\exp (i2\pi /3)\,+\,{m}_{3}\exp (-i2\pi /3)\), where m1,2,3 are respectively the Sz-axis magnetization of the three sublattices, as well as the in-plane spin stiffness ρ31. We locate the three-state Potts transition by examining the crossing of the Binder ratio, and the BKT transition by the criterion ρc = (2/π)Tc.
In the simulations, we use the natural unit in the calculation and thus the following process is required for comparing the model calculation results in the natural unit to experimental data in SI units:
-
(1)
The value of temperature T in natural unit should be multiplied by a factor of Jxy, and change it thus to the unit of Kelvin, where Jxy = 0.88 K is taken as the energy scale in the calculation.
-
(2)
Multiply the value of specific heat Cm in natural unit by a factor of R, i.e., the ideal gas constant, and change it to the unit of J mol−1 K−1.
-
(3)
Multiply the magnetic field h in natural unit by a factor of JxykB/(gzμB) and it is now in unit of Tesla, where gz is the Landé factor along Sz direction and μB the Bohr magneton.
Sample preparation and susceptibility measurements
Single crystals of Na2BaCo(PO4)2 were prepared by the flux method starting from Na2CO3 (99.9%), BaCO3 (99.95%), CoO (99.9%), (NH4)2HPO4 (99.5%), and NaCl (99%), mixed in the ratio 2:1:1:4:5. Details of the heating procedure were given in ref. 14. The flux generated after the reaction is removed by ultrasonic washing. The anisotropic magnetic susceptibility measurements in this work were performed using a SQUID magnetometer (Quantum Design MPMS 3). The magnetic susceptibility as a function of temperature was measured in zero field cooled runs. During the measurements, magnetic field of 0.1 T was applied either parallel or perpendicular to the c axis. In the latter (in-plane) measurements, no anisotropy is observed in the obtained susceptibility data.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
All numerical codes in this paper are available upon request to the authors.
References
Anderson, P. W. Resonating valence bonds: a new kind of insulator? Mater. Res. Bull. 8, 153–160 (1973).
Chubukov, A. V. & Golosov, D. I. Quantum theory of an antiferromagnet on a triangular lattice in a magnetic field. J. Phys. Condens. Matter 3, 69–82 (1991).
Collins, M. F. & Petrenko, O. A. Review/synthése: triangular antiferromagnets. Can. J. Phys. 75, 605–655 (1997).
Starykh, O. A. Unusual ordered phases of highly frustrated magnets: a review. Rep. Prog. Phys. 78, 052502 (2015).
Wessel, S. & Troyer, M. Supersolid hard-core Bosons on the triangular lattice. Phys. Rev. Lett. 95, 127205 (2005).
Melko, R. G. et al. Supersolid order from disorder: hard-core Bosons on the triangular lattice. Phys. Rev. Lett. 95, 127207 (2005).
Heidarian, D. & Damle, K. Persistent supersolid phase of hard-core Bosons on the triangular lattice. Phys. Rev. Lett. 95, 127206 (2005).
Boninsegni, M. & Prokof’ev, N. Supersolid phase of hard-core Bosons on a triangular lattice. Phys. Rev. Lett. 95, 237204 (2005).
Heidarian, D. & Paramekanti, A. Supersolidity in the triangular lattice spin-1/2 XXZ model: a variational perspective. Phys. Rev. Lett. 104, 015301 (2010).
Wang, F., Pollmann, F. & Vishwanath, A. Extended supersolid phase of frustrated hard-core Bosons on a triangular lattice. Phys. Rev. Lett. 102, 017203 (2009).
Jiang, H. C., Weng, M. Q., Weng, Z. Y., Sheng, D. N. & Balents, L. Supersolid order of frustrated hard-core Bosons in a triangular lattice system. Phys. Rev. B 79, 020409 (2009).
Yamamoto, D., Marmorini, G. & Danshita, I. Quantum phase diagram of the triangular-lattice XXZ model in a magnetic field. Phys. Rev. Lett. 112, 127203 (2014).
Yamamoto, D., Marmorini, G., Tabata, M., Sakakura, K. & Danshita, I. Magnetism driven by the interplay of fluctuations and frustration in the easy-axis triangular XXZ model with transverse fields. Phys. Rev. B 100, 140410 (2019).
Zhong, R., Guo, S., Xu, G., Xu, Z. & Cava, R. J. Strong quantum fluctuations in a quantum spin liquid candidate with a Co-based triangular lattice. Proc. Natl Acad. Sci. U.S.A. 116, 14505–14510 (2019).
Li, N. et al. Possible itinerant excitations and quantum spin state transitions in the effective spin-1/2 triangular-lattice antiferromagnet Na2BaCo(PO4)2. Nat. Commun. 11, 4216 (2020).
Lee, S. et al. Temporal and field evolution of spin excitations in the disorder-free triangular antiferromagnet Na2BaCo(PO4)2. Phys. Rev. B 103, 024413 (2021).
Wellm, C. et al. Frustration enhanced by Kitaev exchange in a \({j}_{{{\mbox{eff}}}}=\frac{1}{2}\) triangular antiferromagnet. Phys. Rev. B 104, L100420 (2021).
Liu, H. & Khaliullin, G. Pseudospin exchange interactions in d7 cobalt compounds: possible realization of the Kitaev model. Phys. Rev. B 97, 014407 (2018).
Yu, S., Gao, Y., Chen, B.-B. & Li, W. Learning the effective spin Hamiltonian of a quantum magnet. Chin. Phys. Lett. 38, 097502 (2021).
Chen, L. et al. Two temperature scales in the triangular lattice Heisenberg antiferromagnet. Phys. Rev. B 99, 140404(R) (2019).
Li, H. et al. Thermal tensor renormalization group simulations of square-lattice quantum spin models. Phys. Rev. B 100, 045110 (2019).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992).
Tinkham, M. Group Theory and Quantum Mechanic (Dover Publications, 2003). http://www.loc.gov/catdir/enhancements/fy0615/2003061780-d.html.
Li, Y. et al. Rare-earth triangular lattice spin liquid: a single-crystal study of YbMgGaO4. Phys. Rev. Lett. 115, 167203 (2015).
Li, Y.-D., Wang, X. & Chen, G. Anisotropic spin model of strong spin-orbit-coupled triangular antiferromagnets. Phys. Rev. B 94, 035107 (2016).
Zhu, Z., Maksimov, P. A., White, S. R. & Chernyshev, A. L. Topography of spin liquids on a triangular lattice. Phys. Rev. Lett. 120, 207203 (2018).
Chen, B.-B., Chen, L., Chen, Z., Li, W. & Weichselbaum, A. Exponential thermal tensor network approach for quantum lattice models. Phys. Rev. X 8, 031082 (2018).
Yamamoto, D., Marmorini, G. & Danshita, I. Microscopic model calculations for the magnetization process of layered triangular-lattice quantum antiferromagnets. Phys. Rev. Lett. 114, 027201 (2015).
Sellmann, D., Zhang, X.-F. & Eggert, S. Phase diagram of the antiferromagnetic XXZ model on the triangular lattice. Phys. Rev. B 91, 081104 (2015).
Miyashita, S. & Kawamura, H. Phase transitions of anisotropic Heisenberg antiferromagnets on the triangular lattice. J. Phys. Soc. Jpn. 54, 3385–3395 (1985).
Stephan, W. & Southern, B. W. Monte Carlo study of the anisotropic Heisenberg antiferromagnet on the triangular lattice. Phys. Rev. B 61, 11514–11520 (2000).
Sheng, Q. & Henley, C. L. Ordering due to disorder in a triangular Heisenberg antiferromagnet with exchange anisotropy. J. Phys. Condens. Matter 4, 2937–2959 (1992).
Seabra, L. & Shannon, N. Competition between supersolid phases and magnetization plateaus in the frustrated easy-axis antiferromagnet on a triangular lattice. Phys. Rev. B 83, 134412 (2011).
Kim, E. & Chan, M. H. W. Probable observation of a supersolid helium phase. Nature 427, 225–227 (2004).
Kim, D. Y. & Chan, M. H. W. Absence of supersolidity in solid helium in porous vycor glass. Phys. Rev. Lett. 109, 155301 (2012).
Li, J.-R. et al. A stripe phase with supersolid properties in spin–orbit-coupled bose–einstein condensates. Nature 543, 91–94 (2017).
Léonard, J., Morales, A., Zupancic, P., Donner, T. & Esslinger, T. Monitoring and manipulating higgs and goldstone modes in a supersolid quantum gas. Science 358, 1415–1418 (2017).
Tanzi, L. et al. Supersolid symmetry breaking from compressional oscillations in a dipolar quantum gas. Nature 574, 382–385 (2019).
Norcia, M. A. et al. Two-dimensional supersolidity in a dipolar quantum gas. Nature 596, 357–361 (2021).
Doi, Y., Hinatsu, Y. & Ohoyama, K. Structural and magnetic properties of pseudo-two-dimensional triangular antiferromagnets Ba3MSb2O9 (M = Mn, Co, and Ni). J. Phys. Condens. Matter 16, 8923 (2004).
Shirata, Y., Tanaka, H., Matsuo, A. & Kindo, K. Experimental realization of a spin-1/2 triangular-lattice Heisenberg antiferromagnet. Phys. Rev. Lett. 108, 057205 (2012).
Zhou, H. D. et al. Successive phase transitions and extended spin-excitation continuum in the \(S=\frac{1}{2}\) triangular-lattice antiferromagnet Ba3CoSb2O9. Phys. Rev. Lett 109, 267206 (2012).
Susuki, T. et al. Magnetization process and collective excitations in the S = 1/2 triangular-lattice Heisenberg antiferromagnet Ba3CoSb2O9. Phys. Rev. Lett. 110, 267201 (2013).
Ma, J. et al. Static and dynamical properties of the spin-1/2 equilateral triangular-lattice antiferromagnet Ba3CoSb2O9. Phys. Rev. Lett. 116, 087201 (2016).
Sera, A. et al. \(S=\frac{1}{2}\) triangular-lattice antiferromagnets Ba3CoSb2O9 and CsCuCl3: Role of spin-orbit coupling, crystalline electric field effect, and Dzyaloshinskii-Moriya interaction. Phys. Rev. B 94, 214408 (2016).
Ito, S. et al. Structure of the magnetic excitations in the spin-1/2 triangular-lattice Heisenberg antiferromagnet Ba3CoSb2O9. Nat. Commun. 8, 235 (2017).
Kamiya, Y. et al. The nature of spin excitations in the one-third magnetization plateau phase of \(S=\frac{1}{2}\). Nat. Commun. 9, 2666 (2018).
Rawl, R. et al. Ba8CoNb6O24: A spin-\(\frac{1}{2}\) triangular-lattice Heisenberg antiferromagnet in the two-dimensional limit. Phys. Rev. B 95, 060412(R) (2017).
Cui, Y. et al. Mermin-Wagner physics, (H, T) phase diagram, and candidate quantum spin-liquid phase in the spin-\(\frac{1}{2}\) triangular-lattice antiferromagnet Ba8CoNb6O24. Phys. Rev. Mater. 2, 044403 (2018).
Chen, L. et al. Two-temperature scales in the triangular-lattice Heisenberg antiferromagnet. Phys. Rev. B 99, 140404 (2019).
Hu, Z. et al. Evidence of the Berezinskii-Kosterlitz-Thouless phase in a frustrated magnet. Nat. Commun. 11, 5631 (2020).
Modic, K. A. et al. Scale-invariant magnetic anisotropy in RuCl3 at high magnetic fields. Nat. Phys. 17, 240–244 (2021).
Rost, A. W., Perry, R. S., Mercure, J.-F., Mackenzie, A. P. & Grigera, S. A. Entropy landscape of phase formation associated with quantum criticality in Sr3Ru2O7. Science 325, 1360–1363 (2009).
Fortune, N. A. et al. Cascade of magnetic-field-induced quantum phase transitions in a spin- \(\frac{1}{2}\) triangular-lattice antiferromagnet. Phys. Rev. Lett. 102, 257201 (2009).
Bachus, S. et al. Thermodynamic perspective on field-induced behavior of α-RuCl3. Phys. Rev. Lett. 125, 097203 (2020).
Chen, B.-B., Liu, Y.-J., Chen, Z. & Li, W. Series-expansion thermal tensor network approach for quantum lattice models. Phys. Rev. B 95, 161104(R) (2017).
Li, H. et al. Kosterlitz-Thouless melting of magnetic order in the triangular quantum Ising material TmMgGaO4. Nat. Commun. 11, 1111 (2020).
Li, H. et al. Universal thermodynamics in the Kitaev fractional liquid. Phys. Rev. Res. 2, 043015 (2020).
Li, H. et al. Identification of magnetic interactions and high-field quantum spin liquid in α-RuCl3. Nat. Commun. 12, 4007 (2021).
Chen, B.-B. et al. Quantum many-body simulations of the two-dimensional Fermi-Hubbard model in ultracold optical lattices. Phys. Rev. B 103, L041107 (2021).
Lin, X., Chen, B.-B., Li, W., Meng, Z. Y. & Shi, T. Exciton proliferation and fate of the topological mott insulator in a twisted bilayer graphene lattice model. Phys. Rev. Lett. 128, 157201 (2022).
Yu, S., Gao, Y., Chen, B.-B. & Li, W. QMagen. https://github.com/QMagen (2021).
Acknowledgements
W.L. and Y.G. are indebted to Tao Shi for stimulating discussions, W.L. would also thank Xue-Feng Sun and Jie Ma for valuable discussions on the experiments. This work was supported by the National Natural Science Foundation of China (Grant Nos. 12222412, 11834014, 11874115, 11974036, 11974396, 12047503, and 12174068), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB33020300), and CAS Project for Young Scientists in Basic Research (Grant Nos. YSBR-057 and YSBR-059). We thank the HPC-ITP for the technical support and generous allocation of CPU time.
Author information
Authors and Affiliations
Contributions
W.L., Y.Q., and Y.W. initiated this work. Y.G. and H.L. performed XTRG and DMRG calculations of the TLAF model. Y.W. conducted the symmetry and semi-classical analyses. X.T.Z., F.Y., and X.L.S. did the CEF point charge model analysis and DFT calculations. Y.C.F. undertook the MC simulations. R.Z. prepared the sample and performed the susceptibility measurements. All authors contributed to the analysis of the results and the preparation of the draft. Y.W. and W.L. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gao, Y., Fan, YC., Li, H. et al. Spin supersolidity in nearly ideal easy-axis triangular quantum antiferromagnet Na2BaCo(PO4)2. npj Quantum Mater. 7, 89 (2022). https://doi.org/10.1038/s41535-022-00500-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-022-00500-3
This article is cited by
-
Giant magnetocaloric effect in spin supersolid candidate Na2BaCo(PO4)2
Nature (2024)
-
Magnetocaloric effect of topological excitations in Kitaev magnets
Nature Communications (2024)
-
Magnetism of NaYbS2: From finite temperatures to ground state
Science China Physics, Mechanics & Astronomy (2024)