Spin supersolidity in nearly ideal easy-axis triangular quantum antiferromagnet Na₂BaCo(PO₄)₂

Abstract

Prototypical models and their material incarnations are cornerstones to the understanding of quantum magnetism. Here we show theoretically that the recently synthesized magnetic compound Na₂BaCo(PO₄)₂ (NBCP) is a rare, nearly ideal material realization of the S = 1/2 triangular-lattice antiferromagnet with significant easy-axis spin exchange anisotropy. By combining the automatic parameter searching and tensor-network simulations, we establish a microscopic model description of this material with realistic model parameters, which can not only fit well the experimental thermodynamic data but also reproduce the measured magnetization curves without further adjustment of parameters. According to the established model, the NBCP hosts a spin supersolid state that breaks both the lattice translation symmetry and the spin rotational symmetry. Such a state is a spin analog of the long-sought supersolid state, thought to exist in solid Helium and optical lattice systems, and share similar traits. The NBCP therefore represents an ideal material-based platform to explore the physics of supersolidity as well as its quantum and thermal melting.

Introduction

Quantum magnets are fertile ground for unconventional quantum phases and phase transitions. A prominent example is the S = 1/2 triangular-lattice antiferromagnet (TLAF). Crucial to the conception of the quantum spin-liquid state¹, its inherent geometric frustration and strong quantum fluctuations give rise to exceedingly rich physics. In the presence of an external magnetic field, spin anisotropy, and/or spatial anisotropy, the system exhibits a cornucopia of magnetic orders and phase transitions^2,3,4. In particular, introducing an easy-axis spin exchange anisotropy to the TLAF results in the spin supersolid^{5,6,7,8,9,10,11} in zero magnetic field. Applying a magnetic field along the easy-axis drives the system through a sequence of quantum phase transitions by which the spin supersolidity disappears and then reemerges¹², whereas applying the field in the perpendicular direction yields distinct, even richer behaviors¹³. The S = 1/2 easy-axis TLAF therefore constitutes a special platform for exploring intriguing quantum phases and quantum phase transitions.

Lately, a cobalt-based compound Na₂BaCo(PO₄)₂ (NBCP) has been brought to light^14,15,16,17. This material features an ideal triangular lattice of Co²⁺ ions, each carrying an effective S = 1/2 spin owing to the crystal field environment and the significant spin-orbital coupling^17,18 (Fig. 1a). Early thermodynamic measurements show that NBCP does not order down to ~300 mK with a large magnetic entropy (~2 J mol⁻¹ K⁻¹) hidden below that temperature scale¹⁴. A later thermodynamic measurement reveals a specific heat peak at ~150 mK, which accounts for the missing entropy and points to a possible magnetic ordering in zero magnetic field¹⁵. However, the muon spin resonance (μSR) experiment finds strong dynamical fluctuation down to 80 mK¹⁶ which may suggest a spin-liquid like state. The multitude of experimental results call for a theoretical assessment.

Fig. 1: Crystallographic structure of NBCP and fitting loss landscape.

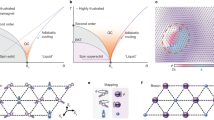
a Top view of the crystallographic structure of the NBCP. Each Co²⁺ ion carries an effective S = 1/2 spin owing to the octahedral crystal environment and the spin-orbital coupling. The spins form a triangular network. Its magnetic ground state is a spin supersolid: the red (blue) circles represent the positive (negative) S^z component, and the black arrows show the direction of the S^x,y component. The crystallographic a-, b-, and c-axes and the spin frame S^x,y,z are shown in the bottom right and the top left insets, respectively. b Shows the projection of the fitting loss function onto the J_xy – J_z plane (with J_PD,Γ fixed as zero), where brighter color represents less fitting loss and therefore better fit. The white cross marks the optimal parameter set, which corresponds to an S = 1/2 TLAF with anisotropy parameter Δ = J_z/J_xy ≃ 1.7 (dashed line).

Previous works have attempted at establishing the spin exchange interactions in this compound. The authors in ref. ¹⁵ suggest an exchange coupling ~2 K based on an analysis of the magnetic susceptibility data, which is an order of magnitude smaller than an earlier estimate of 21.4 K in ref. ¹⁴. Meanwhile, a first-principle calculation suggests potentially significant Kitaev-type exchange interaction¹⁷. Despite these efforts, the precise spin Hamiltonian, its magnetic ground states, as well as the connection to experimental data, are yet to be established.

In this work, we show theoretically that NBCP can be well-described by a S = 1/2 easy-axis TLAF with negligible perturbations. We establish the microscopic description of NBCP with realistic model parameters by fitting the model to intermediate- and high-temperature experimental thermal data. We expedite the fitting process by using the Bayesian optimization¹⁹ equipped with an efficient quantum many-body thermodynamic solver—exponential tensor renormalization group (XTRG)^20,21. Our model is corroborated by reproducing quantitatively the experimental low-temperature magnetization curves by density matrix renormalization group (DMRG)²² calculations. Furthermore, we are able to put the various experimental results into a coherent picture and connect them to the physics of the spin supersolid state. Therefore, the NBCP represents a rare material realization of this prototypical model system and thereby the spin supersolidity. The small exchange energy scale in this material (~1 K) implies that the phases of the NBCP can be readily tuned by weak or moderate magnetic fields. Our results also highlight the strength of the many-body computation-based, experimental data-driven approach as a methodology for studying quantum magnets.

Results

Crystal symmetry and the spin-1/2 model

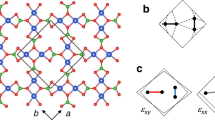
Figure 1a shows the lattice structure of NBCP and the crystallographic a-, b-, and c-axes. Due to the octahedral crystal field environment and the spin-orbital coupling, each Co²⁺ ion forms an effective S = 1/2 doublet in the ground state, which is separated from higher energy multiplets by a gap of ~71 meV (see Supplementary Note 1). Super-super-exchange path through two intermediate oxygen ions produces exchange interactions between two nearest-neighbor (NN) spins, thereby connecting them into a triangular network (see density functional theory calculations in the Supplementary Note 2). Further-neighbor spin exchange interactions are suppressed by the long distance. Meanwhile, the inter-layer exchange interactions are expected to be much smaller than the intra-layer couplings owing to the non-magnetic BaO layer separating the adjacent cobalt layers. Therefore, we model the NBCP in the experimentally relevant temperature window as a S = 1/2 TLAF with dominant NN exchange interactions. This hypothesis will be justified a posteriori.

The crystal symmetry constrains the NN exchange interactions as follows²³. The threefold symmetry axis ∥c passing through each lattice site relates the exchange interactions on the 6 bonds emanating from that site. On a given bond, there is a twofold symmetry axis passing through that bond and a center of inversion. The former symmetry forbids certain components of the off-diagonal symmetric exchange interaction, whereas the latter forbids Dzyaloshinskii-Moriya interactions. We obtain

$${H}_{ij}\,=\,\mathop{\sum}\limits_{\alpha ,\beta }{J}^{\alpha \beta }{S}_{i}^{\alpha }{S}_{j}^{\beta },$$

(1)

with

$${J}^{\alpha \beta }\,=\,\left(\begin{array}{lll}{J}_{xy}\,+\,2{J}_{{{{\rm{PD}}}}}\cos \varphi &-2{J}_{{{{\rm{PD}}}}}\sin \varphi &-{J}_{{{\Gamma }}}\sin \varphi \\ -2{J}_{{{{\rm{PD}}}}}\sin \varphi &{J}_{xy}\,-\,2{J}_{{{{\rm{PD}}}}}\cos \varphi &{J}_{{{\Gamma }}}\cos \varphi \\ -{J}_{{{\Gamma }}}\sin \varphi &{J}_{{{\Gamma }}}\cos \varphi &{J}_{z}\end{array}\right),$$

(2)

where i, j are a pair of neighboring lattice sites, and α, β label the spin x, y, z components^24,25,26. We choose the spin frame such that x∥a, z∥c. $\varphi \,=\,\{0,\frac{2\pi }{3},-\frac{2\pi }{3}\}$ for three different types of NN bonds parallel to a, b, and −(a + b), respectively. J_xy, J_z, J_Γ, and J_PD are respectively the XY, Ising, off-diagonal symmetric, and pseudo-dipolar exchange couplings (see more details in Supplementary Note 3). The entire model parameter space is thus spanned by the four exchange constants, two Landé factors (g_ab and g_c, for perpendicular and parallel to the c-axis, respectively), as well as two van Vleck paramagnetic susceptibilities (${\chi }_{ab}^{{{{\rm{vv}}}}},{\chi }_{c}^{{{{\rm{vv}}}}}$), all of which are taken to be constants in the experimentally relevant temperature/magnetic field window.

Determination of the model parameters

We determine the model parameters in Eq. (1) by fitting the experimental magnetic specific heat (C_m) and magnetic susceptibility (χ) data at temperature T ≥ T_cut, where T_cut = 1 K for C_m and 3 K for χ. Note the magnetic susceptibilities are remeasured in this work with high quality samples. For each trial parameter set, we compute the same thermodynamic quantities from the model by using the XTRG solver^21,27. We search for the parameter set that minimizes the total loss function through an unbiased and efficient Bayesian optimization process¹⁹. See Methods for more details.

We set the cutoff temperature T_cut based on the following considerations. The experimental data from independent measurements agree with each other at T > T_cut, and our XTRG solver does not exhibit significant finite-size effects above T_cut. Meanwhile, the T_cut has to be less than or comparable with the characteristic energy scale of the material. These constraints fix T_cut to our present choices.

The searching process yields the following optimal parameter set: J_xy = 0.88 K, J_z = 1.48 K, and J_Γ,PD are negligible. The Landé factors g_ab = 4.24, and g_c = 4.89. The van Vleck susceptibilities ${\chi }_{ab}^{{{{\rm{vv}}}}}\,=\,0.149$ cm³ mol⁻¹ and ${\chi }_{c}^{{{{\rm{vv}}}}}\,=\,0.186$ cm³ mol⁻¹. To ensure that the algorithm does converge to the global minimum, we project the loss function onto the (J_xy, J_z) plane in Fig. 1b, where, for fixing values of J_xy, J_z, the loss function is minimized over the remaining parameters. The fitting landscape reveals a single minimum. The estimated value of exchange parameters and their bounds of uncertainty are shown in Fig. 2f.

Fig. 2: Thermodynamic data fittings, magnetization curves, and the optimal model parameters.

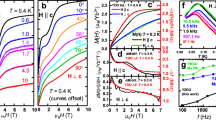
a Shows the magnetic specific heat C_m of the NBCP as a function of temperature T, reported by two independent measurements (Zhong et al.¹⁴ and Li et al.¹⁵) as well as the best fit. The gray dashed line marks T_cut. The XTRG fitting is performed for experimental data at T > T_cut. b, c Show respectively parallel and perpendicular to the c-axis magnetic susceptibilities with the experimental data measured in this work (see Methods) and the best fit. d, e Show the magnetization as a function of the magnetic field in the c and a directions, respectively. The experimental data were obtained from Li et al.¹⁵ with the van Vleck paramagnetic contributions subtracted off. The model prediction is obtained from DMRG, which agrees quantitatively with experiment. The gray lines show magnetization curves obtained from models with various anisotropy parameters Δ, with J_xy tuned to the optimal value. f Shows the standard box plot of the optimal parameters, with the red line indicating the median value, the top(bottom) edge of the box representing the upper(lower) quartile of the best 20 model parameter sets found in 450 Bayesian optimization runs.

The small uncertainties in J_xy and J_z, as well as the small loss, indicate that the experimental data are well captured by our parameters. Indeed, Fig. 2a–c show respectively the specific heat and the magnetic susceptibility as functions of temperature. We find excellent agreement between the model calculations and the experiments within the fitting temperature range T ≥ T_cut. Reassuringly, the Landé factors obtained by us are in excellent agreement with the latest electron-spin resonance measurement (g_ab = 4.24 and g_c = 4.83)¹⁷. We have also calculated the magnetic specific heat C_m in non-zero magnetic fields and find good agreement with the experiments whenever the two independent measurements^14,15 mutually agree (Supplementary Note 4). Note in Fig. 2a the two experimental data sets of specific heat differ at T < T_cut. Our model’s behavior below T_cut is in agreement with one of them. The discrepancy in the experimental data calls for further investigation.

Our model parameters pinpoint to an almost ideal S = 1/2 TLAF with significant easy-axis anisotropy Δ = J_z/J_xy ≈ 1.68. In particular, the negligible off-diagonal exchange interactions imply that the NBCP features an approximate U(1) spin rotational symmetry with respect to c axis. As a result, the magnetization curve with field B∥c in Fig. 2d has a couple of idiosyncratic features: It shows a 1/3-magnetization plateau in an intermediate field range [B_c1, B_c2], and another fully magnetized plateau above the saturation field B_c3. As an independent estimate of Δ, we note the semi-classical analysis shows that ${B}_{c2}/{B}_{c1}\,=\,{{\Delta }}\,-\,1/2\,+\,\sqrt{{{{\Delta }}}^{2}\,+\,{{\Delta }}\,-\,7/4}$ and B_c3/B_c1 = 2Δ + 1 (Supplementary Note 5). Using the experimental values B_c1 ≈ 0.35 T and B_c3 ≈ 1.62 T¹⁵, we estimate Δ ≈ 1.81, which is consistent with the Bayesian search result. Meanwhile, using these numbers, we can estimate B_c2 ≈ 1.10 T, which is fairly close to the experimental value of 1.16 T¹⁵.

As a corroboration of our model, we perform DMRG calculations of the zero-temperature magnetization curves and find quantitative agreement with the experimental results (Fig. 2d, e). With no further adjustment of the parameters, the model can not only produce the correct transition fields but also the details of the magnetization curve between the transitions. We find that the magnetization curve ∥c is a sensitive diagnostic for the anisotropy parameter Δ. The agreement between the model and the experiments is quickly lost when Δ deviates slightly from the optimal value in Fig. 2d.

Taken together, the broad agreements between the semi-classical estimates, the quantum many-body calculations, and experimental data strongly support the S = 1/2 easy-axis TLAF as an effective model description for the NBCP.

Field-tuning of the spin supersolid state

The S = 1/2 easy-axis TLAF exhibits a sequence of magnetic phases and quantum phase transitions driven by magnetic fields^12,28,29. The experimentally measured differential susceptibilities (dM/dB) show a few anomalies when the field is ∥c and ∥a and are attributed to quantum phase transitions¹⁵. Here, we clarify the nature of the magnetic orders of NBCP based on the S = 1/2 easy-axis TLAF model.

Figure 3a shows the theoretical zero-temperature phase diagram of our model in field ∥c, obtained from DMRG calculations. The system goes through successively the Y, Up-Up-Down (UUD), V, and the polarized (P_z) phases with increasing field. These phases are separated by three critical fields B_c1,c2,c3 = 0.36 T, 1.14 T, 1.71 T discussed in the previous section, which are manifested as peaks in dM/dB. The Y phase, as well as the V phase, spontaneously break both the lattice translation symmetry and the U(1) symmetry, thereby constituting the supersolid state analogous to that of the Bose atoms. The UUD phase, on the other hand, restores the U(1) symmetry but breaks the lattice translation symmetry. This state is analogous to a Bose Mott insulator state. The magnetic plateau associated with the UUD state reflects the incompressibility of the Mott insulator.

Fig. 3: Zero-temperature phase diagrams under in- and out-of-plane fields.

a Shows the entanglement entropy and differential magnetic susceptibility dM/dB as functions of field B in the c direction. The Y, UUD, V, and P_z phases are shaded in different colors. B_c1,c2,c3 are the three critical fields separating these phases. The corresponding spin configurations are also shown. Red (blue) circles represent the positive (negative) S^z component. Black arrows show the direction of the in-plane (S^x,y) component. b Is similar to (a) but for field B∥a. The λ phase, $\widetilde{{{{\rm{Y}}}}}$ phase, $\tilde{{{{\rm{V}}}}}$ phase, and P_x phase are separated by three critical fields B_a1,a2,a3. c Is a zoom-in of (b), showing the side view of the spin configurations, as well as the evolution of the order parameter Θ as a function of the field (see main text for definition).

The situation is yet more intricate when the field ∥a. DMRG calculations show that the system goes through the λ, $\tilde{{{{\rm{Y}}}}}$, $\tilde{{{{\rm{V}}}}}$ (see Fig. 3c for an illustration), and the quasi-polarized P_x phases, which are separated by three critical fields B_a1 = 0.075 T, B_a2 = 0.75 T, and B_a3 = 1.51 T. The presence of a field ∥a breaks the U(1)-rotational symmetry with respect to the S^z axis but preserves the π-rotational (Z₂) symmetry with respect to the S^x axis. The λ phase, where the spins sitting on three magnetic sublattices form the greek letter “λ”, spontaneously breaks both the Z₂ symmetry and the lattice translation symmetry. The Z₂ symmetry is restored in the $\tilde{{{{\rm{Y}}}}}$ phase, and spontaneously broken again in the $\tilde{{{{\rm{V}}}}}$ phase.

Comparing to the field-induced transitions in B∥c case, the transitions at B_a1,a2 show much weaker anomalies in dM/dB when B∥a. Numerically, we detect these two transitions using an order parameter ${{\Theta }}\,=\,\frac{1}{\pi }| ({\theta }_{a}\,-\,{\theta }_{b}\,-\,{\theta }_{c})|$, where θ_a,b,c measure the angle between the spin moments on three sublattice and the S^x axis. Θ = 0 when the Z₂ symmetry is respected and Θ ≠ 0 when it is broken. Figure 3c shows Θ as a function of field, from which we can delineate the boundaries between λ, $\tilde{{{{\rm{Y}}}}}$, and $\tilde{{{{\rm{V}}}}}$ phases, with the critical fields B_a1 ≈ 0.07 T and B_a2 ≈ 0.75 T. The small value of B_a1 implies it could be easily missed in experiments. Meanwhile, the weak anomalies in dM/dB associated with B_a1,a2 make them difficult to detect in thermodynamic measurements. We note that dM/dB shows a broad peak in the $\tilde{{{{\rm{Y}}}}}$ phase at ~0.4–0.5 T¹⁵. This peak appears in the experimental data and was previously interpreted as a transition. The true transitions (B_a1,a2) are in fact above and/or below the said peak. We also note that, despite of the weak anomaly observed numerically at B_a2, the quantum phase transition there is likely of first-order from symmetry analysis: the $\tilde{{{{\rm{Y}}}}}$ and $\tilde{{{{\rm{V}}}}}$ phases both have a sixfold ground-state degeneracy and they have incompatible symmetry breaking; thus the transition cannot be continuous according to Landau’s paradigm.

Strong spin fluctuations and phase diagram at finite temperature

Having established the zero-temperature phase diagram of the NBCP, we now move on to its physics at finite temperature. Figure 4a shows the contour plot of C_m/T as a function of temperature and field B∥c. In the temperature window accessible to the XTRG, we find a broad peak near zero field, which moves to higher temperature and becomes sharper as field increases. These features are in qualitative agreement with the experimental findings.

Fig. 4: Finite-temperature phase diagram of the NBCP under magnetic fields ∥c.

a Shows C_m/T, calculated from XTRG, as a function of temperature T and magnetic field ∥c. The open squares mark the peaks of the experimental C_m/T data (Li et al.¹⁵). b Shows C_m/T under zero field, and the magnetic entropy S_m, as functions of temperature. The experimental S_m data are obtained by integrating numerically the C_m/T data. The experimental entropy curve is shifted by 0.55 Jmol⁻¹K⁻¹ to match the saturation value $R\ln (2)$ at sufficiently high temperature. c Shows the temperature-field phase diagram constructed from the classical Monte Carlo (MC) simulation. The blue triangles mark the three-state Potts transitions determined by using the Binder cumulants. Red solid circles mark the BKT transitions determined from the spin stiffness (see Methods). The zero field BKT transition temperatures are reported by ref. ³¹. The red solid line along the vertical axis under zero field indicates the regime with algebraic spin correlation in the S^z spin component. d Shows the specific heat as a function of temperature for various representative magnetic field ∥c, obtained from the classical MC simulation.

Figure 4b shows a cross-section of the contour plot at zero field. The model produces a peak in C_m/T at ≈ 150 mK, which is in excellent agreement with the experimental data from ref. ¹⁵. Note this temperature is well below the temperature window (above T_cut) used for fitting, the difference between theory and experiment at very low temperatures may be ascribed to the finite-size effect inherent in the XTRG calculations (see Methods). The magnetic entropy also shows quantitative agreement with the experimental data. In particular, there is still a considerable amount of magnetic entropy to be released at 300 mK (and even down to 150 mK). The missing entropy at 300 mK reported in ref. ¹⁴ can be ascribed to the small spin interaction energy scale and high degrees of frustration in the NBCP.

To understand the finite-temperature phase diagram of the NBCP, we perform a Monte Carlo (MC) simulation of the classical TLAF model with appropriate rescaling of temperature and magnetic field^30,31,32,33. This approximation is amount to neglecting fluctuations in the imaginary time direction in the coherent-state path integral of the S = 1/2 TLAF. As the finite-temperature phase transitions are driven by thermal fluctuations, we expect that the salient features produced by the classical MC simulations are robust. Meanwhile, the MC simulation allows for accessing much larger system sizes and lower temperatures comparing to the XTRG for quantum model simulations.

The physics of the classical TLAF model is well documented; here, we focus on the features that can be directly compared with available experimental data. Figure 4c shows the MC-constructed T-B phase diagram with B∥c. Figure 4d shows the specific heat as a function of temperature for various representative fields. The phase diagram shows a broad dome of UUD phase, beneath which lie the Y phase at low field and the V phase at high field. The UUD phase and the paramagnetic phase are separated by a transition of three-state Potts universality; the Y and V phases and the UUD phase are seperated by the Berezinskii-Kosterlitz-Thoueless (BKT) transitions. Note the MC simulation may seem to suggest the onset of the V phase precedes that of the UUD phase at high field; this is an finite-size effect. On symmetry ground, we expect that the onset of the UUD phase either precedes that of the V phase through two continuous transitions, or the system enters the V phase directly through a first-order transition.

At zero field, the specific heat shows two broad peaks, which are related to the two BKT transitions accompanying the onset of the algebraic long-range order in S^z and S^x components, respectively^30,31. The experimentally observed specific heat peak ~150 mK may be related to the higher-temperature BKT transition; the lower-temperature BKT transition (around 54 mK as estimated by classical MC simulations) is yet to be detected as they lie below the temperature window probed by the previous experiments. The strong dynamical spin fluctuations found in μSR experiment at 80 mK is naturally attributed to the algebraic long-range order in the S^z component. Note there exists arguments for a third BKT transition³² although it is not observed in classical MC simulations³¹.

When the magnetic field is switched on, the specific heat shows a sharp peak signaling the three-state Potts transition from the high-temperature paramagnetic phase to the UUD phase, corresponding to onset of the long-range order in the S^z component. This is consistent with the experimentally observed sharp specific heat peak at finite fields¹⁵. At lower temperature, the specific heat shows a much weaker peak related to the BKT transition into either the Y phase or the V phase, corresponding to the onset of the algebraic long-range order in S^x. The lower-temperature BKT transitions are yet to be detected by experiments.

Discussion

The supersolid, a spatially ordered system that exhibits superfluid behavior, is a long-pursued quantum state of matter. The question of whether such a fascinating phase of matter exists in nature has spurred intense research activity, and the search for supersolidity has become a multidisciplinary endeavor^{34,35,36,37,38,39}. The early claim of observation in He-4³⁴ turned out to be an experimental artifact³⁵. Nevertheless, it has inspired new lines of research in ultracold quantum gases^36,37,38,39. Meanwhile, it has been proposed theoretically that the ultracold Bose atoms in a triangular optical lattice can host a supersolid state^5,6,7,8. Yet, the realization of such a proposal has not been reported up to date.

An equivalent, yet microscopically different route to the triangular-lattice supersolidity is via the easy-axis S = 1/2 TLAF magnet. The spin up/down state of a magnetic ion can be viewed as the occupied/empty state of the lattice site by a Bose atom, and the spin rotational symmetry with respect to the easy axis is mapped to the U(1) phase rotation symmetry. By virtue of this mapping, the spin ground state in the easy-axis TLAF, which spontaneously breaks both lattice translation symmetry and spin rotational symmetry, is equivalent to the supersolid state of Bose atoms.

Despite its simple setting, ideal S = 1/2 TLAF has rarely been found in real materials. Although TLAFs with higher spin (S > 1/2) are known³, S = 1/2 systems with equilateral triangular-lattice geometry, such as Ba₃CoSb₂O₉^{40,41,42,43,44,45,46,47} and Ba₈CoNb₆O₂₄^48,49, were synthesized and characterized not until recently. The former shows easy-plane anisotropy^28,47, whereas the latter material is thought to be nearly spin isotropic^48,49,50. To the best of our knowledge, ideal S = 1/2 easy-axis TLAFs are yet to be found. In this work, we show that the NBCP is an almost ideal material realization of such an S = 1/2 easy-axis TLAF with the anisotropy parameter Δ ≈ 1.7.

Our model arranges the various pieces of available experimental data into a coherent picture by connecting them to the rich physics of the TLAF model. It permits a quantitative fit of the thermodynamic data, including specific heat C_m and magnetic susceptibility χ down to intermediate and even low temperatures. In particular, we obtain the C_m/T peak at around 150 mK observed in experiments¹⁵, which we associate to the BKT transition. Furthermore, we are able to accurately reproduce the spin state transition fields observed in previous AC susceptibility measurements along both a and c axes and clarify their nature.

The obtained spin exchange interactions are on similar orders of magnitude as previous estimation based on the Curie-Weiss fitting of the magnetic susceptibility¹⁵ and first-principle calculation¹⁷. However, the first-principle calculation suggests a significant Kitaev-type exchange interaction (in a rotated spin frame)¹⁷, whereas our model, being directly fitted from the experimental data, possesses a nearly ideal U(1) symmetry and negligible Kitaev-type interaction (see more discussions in Supplementary Note 3). The nearly ideal U(1) symmetry in this material is indicated by the well-quantized magnetization plateau (Fig. 2d), which would be absent without the U(1) symmetry.

In our fitting procedure, we have omitted at the outset all further-neighbor exchange interactions on the ground that their magnitude must be suppressed by the large distance between further-neighbor Co²⁺ ions. This can be verified by including in the model a second-neighbor spin-isotropic exchange interaction J₂. To verify it, we have performed additional 400 Bayesian iterations and find J₂ with the median value ~0.1 K amongst the best 20 parameter sets, which are negligibly small. We thus conclude the obtained optimal parameters in the simulations are robust.

Despite the essential challenge in the first-principle calculations of the strongly correlated materials, we may nevertheless employ the density functional theory (DFT) + U approach to justify certain aspects of the microscopic spin model that are accessible to this approach. First of all, we find the charge density distributions of 3d electrons of Co²⁺ ions are well separated from one triangular plane to another (see Supplementary Note 2), which ensures two-dimensionality of the compound. Moreover, the in-plane charge density distribution reveals clearly a super-super-exchange path between the two NN Co²⁺ ions. We construct the Wannier functions of d-orbitals of Co²⁺ ions and extract the hopping amplitude t between two NN Co²⁺ ions. From the second-order perturbation theory in t/U, the NN exchange coupling can be estimated to be on the order of 2–3 K for moderate and typical U_eff = 4–6 eV in this Co-based compound¹⁷, which is consistent with the energy scales of the spin model.

The accurate model for the NBCP also points to future directions for the experimentalists to explore. The model hosts a very rich phase diagram in both temperature and magnetic field, which are yet to be fully uncovered by experiments. In particular, the model shows a second BKT transition at ~50 mK in zero field; in finite field B∥a, the model shows two subtle transitions at B_a1 ≈ 0.07 T and B_a2 ≈ 0.75 T. These transitions may be detected by nuclear magnetic resonance⁵¹, magneto-torque measurements⁵², and magnetocaloric measurements^53,54,55. Neutron scattering experiments can also be employed to detect the simultaneous breaking of discrete lattice symmetry and spin U(1) rotational symmetry, as well as the behaviors of spin stiffness, so as to observe spin supersolidity in this triangular quantum magnet. On the theory front, while the S = 1/2 easy-axis TLAF and its classical counterpart share similar features in their finite-temperature phase diagrams, it was realized early on that the quantum model also possess peculiar traits that are not fully captured by the classical model³². Clarifying these subtleties in the context of NBCP would also presents an interesting problem for the future.

Methods

Exponential tensor renormalization group

The thermodynamic quantities including the magnetic specific heat C_m, and magnetic susceptibility χ can be computed with the exponential tensor renormalization group (XTRG) method^21,27. In practice, we perform XTRG calculations on the Y-type cylinders with width W = 6 and length up to L = 9 (denoted as YC6 × 9, see Supplementary Note 4), and retain up to D = 400 states with truncation errors ϵ ≲ 1 × 10⁻⁴ (down to 1 K) and ≲1 × 10⁻³ (down to about 100 mK). The XTRG truncation provides faithful estimate of error in the computed free energy, and the small ϵ values thus guarantee high accuracy of computed thermal data down to low temperature.

The XTRG simulations start from the initial density matrix ρ₀(τ) at a very high-temperature T ≡ 1/τ (with the inverse temperature τ ≪ 1), represented in a matrix product operator (MPO) form⁵⁶. The series of density matrices ρ_n(2ⁿτ) (n ≥ 1) at lower temperatures are obtained by iteratively multiplying and compressing the MPOs ρ_n = ρ_n − 1 ⋅ ρ_n − 1. As a powerful thermodynamic solver, XTRG has been successfully applied in solving triangular-lattice spin models⁵⁰ and related compounds^51,57, Kitaev model⁵⁸ and materials⁵⁹, correlated fermions in ultracold quantum gas⁶⁰, and even moiré quantum materials⁶¹.

Automatic parameter searching

By combining the thermodynamic solver XTRG and efficient Bayesian optimization approach, the optimal model parameters can be determined automatically via minimizing the fitting loss function between the experimental and simulated data, i.e.,

$${{{\mathcal{L}}}}({{{\bf{x}}}})\,=\,\frac{1}{{N}_{\alpha }}\mathop{\sum}\limits_{\alpha }\frac{{({O}_{\alpha }^{\exp }\,-\,{O}_{\alpha }^{\mathrm{sim} ,{{{\bf{x}}}}})}^{2}}{{({O}_{\alpha }^{\exp })}^{2}}.$$

(3)

${O}_{\alpha }^{\exp }$ and ${O}_{\alpha }^{\mathrm{sim} ,{{{\bf{x}}}}}$ are respectively the experimental and simulated quantities with given model parameters ${{{\bf{x}}}}\,\equiv\, \{{J}_{xy},{J}_{z},{J}_{{{{\rm{PD}}}}},{J}_{{{\Gamma }}},{g}_{ab,c},{\chi }_{ab,c}^{{{{\rm{vv}}}}}\}$. The index α labels different physical quantities, e.g., magnetic specific heat and susceptibilities, and N_α counts the number of data points in O_α. The optimization of ${{{\mathcal{L}}}}$ over the parameter space spanned by {J_xy, J_z, J_PD, J_Γ} is conducted via the Bayesian optimization¹⁹. The Landé factor g_ab,c and the Van Vleck paramagnetic susceptibilities ${\chi }_{ab,c}^{{{{\rm{vv}}}}}$ are optimized via the Nelder-Mead algorithm for each fixing {J_xy, J_z, J_PD, J_Γ}. In practice, we perform the automatic parameter searching using the package QMagen developed by some of the authors^19,62, and the results shown in the main text are obtained via over 450 Bayesian iterations. After that, we introduce an additional parameter, the next-nearest-neighbor Heisenberg term J₂, and perform another 400 searching iterations. We find J₂ is indeed negligibly small and the obtained optimal parameters are robust.

Density matrix renormalization group

The ground-state magnetization curves of the easy-axis TLAF model for NBCP are computed by the density matrix renormalization group (DMRG) method²², which is a powerful variational algorithm based on the matrix product state ansatz. The DMRG simulations are performed on YC6 × 15 lattice, and we retain bond dimension up to D = 1024 with truncation error ϵ < 3 × 10⁻⁵, which guarantees well converged DMRG data.

Classical Monte Carlo simulations

We replace the S = 1/2 operators by classical vectors, ${S}_{i}^{x,y,z}\,\to\, S{\hat{n}}_{i}$, where ${\hat{n}}_{i}$ is a unit vector, and S = 1/2 is the spin quantum number. We use the standard Metropolis algorithm with single spin update. The largest system size is 48 × 48. We compute the Binder ratio associated with the UUD-phase order parameter $\psi \,=\,{m}_{1}\,+\,{m}_{2}\exp (i2\pi /3)\,+\,{m}_{3}\exp (-i2\pi /3)$, where m_1,2,3 are respectively the S^z-axis magnetization of the three sublattices, as well as the in-plane spin stiffness ρ³¹. We locate the three-state Potts transition by examining the crossing of the Binder ratio, and the BKT transition by the criterion ρ_c = (2/π)T_c.

In the simulations, we use the natural unit in the calculation and thus the following process is required for comparing the model calculation results in the natural unit to experimental data in SI units:

• (1) The value of temperature T in natural unit should be multiplied by a factor of J_xy, and change it thus to the unit of Kelvin, where J_xy = 0.88 K is taken as the energy scale in the calculation.

• (2) Multiply the value of specific heat C_m in natural unit by a factor of R, i.e., the ideal gas constant, and change it to the unit of J mol⁻¹ K⁻¹.

• (3) Multiply the magnetic field h in natural unit by a factor of J_xyk_B/(g_zμ_B) and it is now in unit of Tesla, where g_z is the Landé factor along S_z direction and μ_B the Bohr magneton.

Sample preparation and susceptibility measurements

Single crystals of Na₂BaCo(PO₄)₂ were prepared by the flux method starting from Na₂CO₃ (99.9%), BaCO₃ (99.95%), CoO (99.9%), (NH₄)₂HPO₄ (99.5%), and NaCl (99%), mixed in the ratio 2:1:1:4:5. Details of the heating procedure were given in ref. ¹⁴. The flux generated after the reaction is removed by ultrasonic washing. The anisotropic magnetic susceptibility measurements in this work were performed using a SQUID magnetometer (Quantum Design MPMS 3). The magnetic susceptibility as a function of temperature was measured in zero field cooled runs. During the measurements, magnetic field of 0.1 T was applied either parallel or perpendicular to the c axis. In the latter (in-plane) measurements, no anisotropy is observed in the obtained susceptibility data.