Abstract
The recently discovered kagome superconductor CsV3Sb5 (Tc ≃ 2.5 K) has been found to host charge order as well as a non-trivial band topology, encompassing multiple Dirac points and probable surface states. Such a complex and phenomenologically rich system is, therefore, an ideal playground for observing unusual electronic phases. Here, we report anisotropic superconducting properties of CsV3Sb5 by means of transverse-field muon spin rotation (μSR) experiments. The fits of temperature dependences of in-plane and out-of-plane components of the magnetic penetration depth suggest that the superconducting order parameter may have a two-gap (s + s)-wave symmetry. The multiband nature of superconductivity could be further supported by the different temperature dependences of the anisotropic magnetic penetration depth γλ(T) and upper critical field \({\gamma }_{{{{{\rm{B}}}}}_{{{{\rm{c}}}}2}}(T)\). The relaxation rates obtained from zero field μSR experiments do not show noticeable change across the superconducting transition, indicating that superconductivity does not break time reversal symmetry.
Similar content being viewed by others
INTRODUCTION
The kagome lattice materials, consisting of a two-dimensional lattice of corner-sharing triangles, have drawn considerable attention in recent years1,2,3,4. Their electronic structure is characterized by a dispersionless flat band, whose origin lies in the innate kinetic frustration of the kagome geometry, and a pair of Dirac points5. Such flat bands, with a high density of electronic states, are generally perceived to quench the kinetic energy and to induce correlated electronic phases when found close to the Fermi level6,7, as illustrated by the recently discovered superconducting twisted bilayer graphene5. The inherent geometrical frustration of kagome systems can be employed to carefully tune their properties, thus aiding in the search of superconductors (SC) with non-phonon mediated pairing mechanisms8. A recent example of a kagome superconductor with unconventional coupling is LaRu3Si28. Here, the correlation effects from the kagome flat band, the van Hove points on the kagome lattice, and the high density of states from the narrow electronic bands were proposed as key factors for achieving a relatively high transition temperature Tc ≃ 7 K.
Following the recent discovery of the AV3Sb5 (A = K, Rb, Cs) family of kagome materials9, a slew of interesting and exotic effects have been observed: giant anomalous Hall conductivity10,11,12, magneto-quantum oscillations10,13, topological charge order14,15,16,17,18,19, orbital order20, and superconductivity21,22,23,24. Featuring a kagome network of vanadium atoms interwoven with a simple hexagonal antimony net, the normal state of CsV3Sb5 was described as a nonmagnetic Z2 topological metal21,22. Furthermore, the observation of CDW order in the normal state of all members of AV3Sb5 kagome family has generated significant theoretical and experimental interest. Namely, topological chiral charge order has been reported in AV3Sb5 (A = K, Rb, or Cs)14,16. In KV3Sb5, direct evidence for time-reversal symmetry breaking by the charge order was demonstrated using muon spin rotation25.
Regarding superconductivity, a strong diversity in the SC gap symmetry is reported in AV3Sb5 family. Proximity-induced spin-triplet pairing was suggested for K1−xV3Sb526. For CsV3Sb5, in particular, there are significant differences in concluding the superconducting gap structure. For instance, multiband superconductivity with sign-preserving order parameter was reported by means of scanning tunneling microscopy (STM) measurements at ultralow temperature27, and magnetic penetration depth measurements using tunnel diode oscillator techniques28. Contrarily, a nodal type superconducting gap symmetry is proposed through thermal conductivity measurements29. Finally, reentrant superconductivity and double SC domes were found under pressure30,31,32. From a theoretical perspective, several scenarios for electronically mediated, unconventional superconductivity have been discussed33. The AV3Sb5 electronic bands exhibit van Hove singularities close to the Fermi energy—an electronic structural motif shared with other systems, such as the cuprate superconductors or Sr2RuO4. A particular feature of the kagome lattice, however, is a sublattice interference mechanism34, by which the Bloch states near each van Hove point are supported on a distinct sublattice. This promotes the relevance of long-range interactions and unconventional pairing states.
To explore unconventional aspects of superconductivity in CsV3Sb5, it is critical to measure the superconducting order parameter on the microscopic level through measurements of the bulk properties. Thus, we focus on muon spin rotation/relaxation (μSR) measurements of the magnetic penetration depth35 λ in CsV3Sb5. λ is one of the fundamental parameters of a superconductor, since it is related to the superfluid density ns via:
where m* is the effective mass. Most importantly, the temperature dependence of λ is particularly sensitive to the topology of the SC gap: while in a fully gapped superconductor, \({{\Delta }}{\lambda }^{-2}\left(T\right)\equiv {\lambda }^{-2}\left(0\right)-{\lambda }^{-2}\left(T\right)\) vanishes exponentially at low T, whereas in the case of a clean system with line nodes it shows a linear T-dependence.
RESULTS
Sample characterization
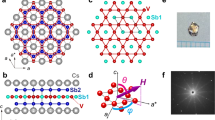
To determine sample purity, X-ray diffraction experiments were performed on flux-grown crystals. The powder diffraction pattern of ground crystals can be well fitted using the structure of CsV3Sb5 and the fitted lattice parameters are a = 5.50552(2) Å and c = 9.32865(3) Å, close to the previous results22. Additionally, to test the single crystallinity of the samples and determine the orientation for the μSR experiments, X-ray Laue diffraction was performed on the single crystal shown in Fig. 1a, whose diffraction pattern is displayed in Fig. 1c. The crystal was easily aligned; the hexagonal symmetry of the ab-plane is clearly visible from the single crystal, and the crystals grow with the c-axis aligned along the thin direction of the crystal. The diffraction pattern collected in Fig. 1c was analyzed with the OrientExpress program36 and the orientation was confirmed to be along the crystallographic c-axis.
a Optical microscope photograph of a single crystal with the crystallographic axes highlighted by arrows. Notice the obvious hexagonal symmetry. b Laue x-ray diffraction image of the single crystal along the 001 direction. c X-ray diffraction pattern obtained from a single crystal sample. d Temperature dependence of magnetic susceptibility in an applied field of 1 mT along the ab plane highlighting the superconducting transition. e Temperature dependence of magnetic susceptibility in an applied field of 1 T along the c axis emphasizing the CDW transition at 95 K. f Electrical resistivity as a function of temperature under zero applied field.
The superconductivity of the samples was confirmed by magnetization [Fig. 1d] and resistivity [Fig. 1f] experiments, which show a diamagnetic shift in the sample concurrent with the onset of zero-resistivity at Tc ≃ 2.7 K which is slightly higher than the compared to the Tc (= 2.5 K) value obtained from magnetization measurements. This is most likely due to very tiny filamentary superconducting channels. The onset of charge order is visible in the magnetization measurements in Fig. 1e, corresponding to the anomaly at Tco ≈ 95 K. There is also a slight change in slope visible in the resistivity data presented in Fig. 1f, which occurs at the onset of the charge-ordered state.
Anisotropy in magnetic penetration depth and superconducting gap structure
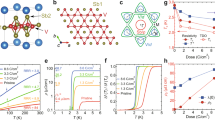
Two sets of TF-μSR experiments were carried out in the field-cooled state, with the external magnetic field applied parallel to the c − axis, and parallel to the ab (kagome) plane. In both cases the muon spin was perpendicular to the applied field. Note that, for an applied field parallel to the c-axis, the screening currents around the flux-line cores flow in the ab-plane. This allows us to determine the so-called in-plane component of the magnetic penetration depth λab. The TF-μSR time-spectra collected with an external field Bext = 10 mT applied parallel to the c-axis above (T = 5 K) and well below (T ≃ 0.27 K) the superconducting transition temperature Tc ≃ 2.5 K are shown in Fig. 2a. The corresponding Fourier transforms of the TF-μSR data, representing the magnetic field distribution P(B), are shown in Fig. 2b. The insets in Fig. 2a and Fig. 2b, respectively, represent the geometry of the experiment and the schematic distribution of the magnetic fields within the isotropic flux-line lattice (FLL) with the two components of the magnetic penetration depth, namely λa and λb being equal: λa = λb = λab. The TF-μSR time-spectra and the corresponding Fourier transforms collected with Bext = 10 mT applied along the kagome plane are presented in Fig. 2c and d, respectively. With the field applied along the ab-plane, the screening currents around the vortex cores flow along the ab-plane and c-axis, thus implying that in a set of experiments with B∥ab, λab,c can be determined. Note that, due to the anisotropy, λc is longer than λab, which leads to an elongation of the vortex lattice along the c direction [see inset in Fig. 2d].
a and c TF-μSR spectra collected above and below Tc for CsV3Sb5 with Bext∣∣c and Bext∣∣ab, respectively. The fast damping of the signal in the superconducting state reflects the inhomogeneous field distribution sensed by the muon ensemble as a result of vortex formation. Solid lines through the data points are fits using Eq. (5) in the Suppl. Inset: Scheme of the setup for μSR experiments on a single crystalline CsV3Sb5 sample. b and d show the Fourier spectra obtained by fast Fourier transformation of the spectra in a and c, respectively. The inset shows the spatial field variation within a flux line lattice of an anisotropic superconductor with an anisotropy parameter γλ ≃ 3, as explained in detail in Refs. 72,75. The cutoff at low fields corresponds to the minimum in P(B) occurring at the midpoint of three adjacent vortices (\({B}_{\min }\)). The peak in P(B) arises from the saddle point midway between two adjacent vortices (Bsaddle), whereas the long tail towards high fields is due to the region around the vortex cores (\({B}_{\max }\)). e Temperature variation of the square-root of the second moment of field distribution σ(T) [\(\sigma ={M}_{2}^{1/2}\)], as measured for the two applied field directions. The horizontal lines denote the relaxation due to nuclear magnetic moments along the two directions. f Internal magnetic field as a function of temperature in the superconducting state. A clear diamagnetic shift, an immanent feature of type-II superconductors, can be seen. g Temperature variation of the skewness parameter, \({\alpha }_{{{{\rm{sk}}}}}={M}_{3}^{1/3}/{M}_{2}^{1/2}\), for the Bext∣∣c and Bext∣∣ab set of experiments. The error bars represent the SD of the fit parameters.
The formation of the flux-line lattice (FLL) in the superconductor leads to a nonuniform magnetic field distribution between the vortices [see insets in Fig. 2b and d]. The strong damping of the TF-μSR time-spectra [Fig. 2a and c] and the corresponding broadening of the Fourier transform [Fig. 2b and d] represent exactly this effect. Note that the measured distribution of the magnetic fields in the superconducting state becomes asymmetric, as expected for a well-arranged FLL. All the characteristic features, as e.g., the cutoff at low fields (\({B}_{\min }\)), the peak due the saddle point between two adjacent vortices (Bsad), and the long tail towards high fields, related to the regions around the vortex core (\({B}_{\max }\)), are clearly visible for Bext∣∣c. However. the asymmetric shape is not observed in case of Bext∣∣ab for two reasons: (i) Long λc: long λ leads to smaller field variation within the vortex lattice. (ii) High value of the nuclear moment contribution σnm: since the asymmetric line shape caused by the formation of the vortex lattice needs to be convoluted with σnm37, which effectively leads to a smearing out the characteristic features of the vortex lattice. The locations of \({B}_{\min }\), Bsad, and \({B}_{\max }\) are shown in the contour plot in the inset of Fig. 2b. To account for the field distribution P(B), the time-domain spectra were analyzed using a skewed Gaussian (SKG) function, which represents the simplest distribution accounting for the asymmetric lineshape (see Suppl. Mater. for a detailed description of the function).
The parameters obtained from the fits are presented in Fig. 2e–g. Figure 2e shows the temperature dependence of the square root of the second moment M2 (see Suppl. Mater. for detailed calculations) which corresponds to the total depolarization rate σ for two field orientations. Below Tc, the relaxation rate σ starts to increase from its normal-state value due to the formation of the FLL and saturates at low temperatures. The normal-state muon depolarization rate is mostly due to the nuclear magnetic moments and, for CsV3Sb5, it has different values for the two field orientations, \({\sigma }_{{{{\rm{nm}}}}}^{| | c}\) = 0.165(3) μs−1 and \({\sigma }_{{{{\rm{nm}}}}}^{| | ab}\) = 0.287(3) μs−1 [shown by horizontal lines in Fig. 2e]. As shown in Fig. 2f, for both field orientations the first moment—which represents the internal field (Bint)—shows a clear diamagnetic shift below Tc, as expected for a type-II superconductor. Note that the Tc value estimated from μSR experiments agrees with that determined from magnetization measurement, so that \({T}_{{{{\rm{c}}}}}^{\mu {{{\rm{SR}}}}}={T}_{{{{\rm{c}}}}}^{{{{\rm{\chi }}}}}\simeq 2.5\) K.
The asymmetric line shape of the field distribution P(B) is characterized by the third moment (M3) of the field distribution (see Suppl. Mater. for the calculations) and has three characteristic fields: \({B}_{\min }\), \({B}_{\max }\), and Bsad. More accurately, the asymmetry of the line shape is described by its skewness parameter \({\alpha }_{{{{\rm{sk}}}}}=({M}_{3}^{1/3}/{M}_{2}^{1/2})\), which assumes a value of 1.2 for a perfectly arranged triangular vortex lattice38,39. Distortions or even melting of the vortex lattice structure, which may be caused by variations of temperature or magnetic field, are strongly reflected in αsk40,41,42.
Figure 2 (g) shows the temperature evolution of \({\alpha }_{{{{\rm{sk}}}}}^{| | c}\) (for Bext∣∣c) and \({\alpha }_{{{{\rm{sk}}}}}^{| | ab}\) (for Bext∣∣ab) for the kagome superconductor CsV3Sb5. Notably, in both directions, αsk(T) remains independent of temperature for T ≲ Tc, with a constant value of ≃ 0.8 for \({\alpha }_{{{{\rm{sk}}}}}^{| | ab}\) and 0.9 for \({\alpha }_{{{{\rm{sk}}}}}^{| | c}\), respectively. We note that near the superconducting transition temperature the μSR response could be well fitted by the single Gaussian line (i.e., the reduced χ2 of SKG and single Gaussian fits become almost equal). Since for the symmetric P(B) distribution αsk stays exactly at zero, this leads to the sudden change of αsk at T ~ 2.2 K, i.e., ≃ 0.3 K below Tc. This observation suggests that very close to Tc, the FLL is slightly distorted but does not disturb the determination of the temperature evolution of the superfluid density along different crystallographic directions (as we show later), which is the main goal of the present study.
We estimate the superconducting contribution to the depolarization rate, σsc, by quadratically subtracting the temperature-independent nuclear magnetic moment contribution σnm (obtained above Tc) from the the total depolarization rate σ (i.e., \({\sigma }_{{{{\rm{sc}}}}}^{2}={\sigma }^{2}-{\sigma }_{{{{\rm{nm}}}}}^{2}\)).
σsc can be expressed as a function of the reduced field b = \(\frac{B}{{B}_{{{{\rm{c}}}}2}}\) (Bc2 being the upper critical field) and the Ginzburg-Landau coefficient κ by the relation developed by Brandt43,44
where λ is the magnetic penetration depth. Thus, we obtain the temperature dependence of \({\lambda }_{{{{\rm{ab}}}}}^{-2}\) (for Bext∥c) and \({\lambda }_{{{{\rm{ab,c}}}}}^{-2}\) (for Bext∥ab). In the case of an anisotropic superconductor, the magnetic penetration depth is also anisotropic. In the present case, by considering an anisotropic effective mass tensor, \({\lambda }_{{{{\rm{ab}}}}}^{-2}\) and \({\lambda }_{{{{\rm{ab,c}}}}}^{-2}\), \({\lambda }_{{{{\rm{c}}}}}^{-2}\) can be estimated (see Suppl. Mater. for the detailed analysis). In this way, we can directly compare the anisotropy of the magnetic penetration depth. Figure 3a and b shows the temperature evolution of \({\lambda }_{{{{\rm{ab}}}}}^{-2}\) and \({\lambda }_{{{{\rm{c}}}}}^{-2}\), respectively.
a and b Temperature variations of the in-plane and out-of-plane component of the inverse squared magnetic penetration depths, \({\lambda }_{ab}^{-2}(T)\) and \({\lambda }_{c}^{-2}(T)\). Data are fitted with a two gap (s + s)-wave, and a nodal d-wave model, as described by the phenomenological α-model. c Magnetic penetration depth anisotropy (γλ) and upper critical field anisotropy (\({\gamma }_{{B}_{{{{\rm{c}}}}2}}\)) as a function of temperature. \({\gamma }_{{B}_{{{{\rm{c}}}}2}}(T)\) is obtained by considering the SC transition temperature Tc as the temperature where resistivity approaches zero. The error bars represent the SD of the fit parameters.
As mentioned in the introduction, there are only a few studies involving different experimental techniques to address the superconducting gap structure of the CsV3Sb5 kagome superconductor. However, there is no consensus among them. To determine whether the superconducting gap structure of this compound is of single-gap, multigap, or even of nodal nature, we analyzed the temperature dependence of magnetic penetration depth. We analyzed λ(T) data using the following expression:
where \(f={(1+E/{k}_{{{{\rm{B}}}}}T)}^{-1}\) represents the Fermi-distribution function. The temperature- and angle-dependent gap function is described by Δ(T, ϕ) = Δ0δ(T/Tc)g(ϕ), where Δ0 is the maximum gap value at T = 0, while the temperature dependence of the gap function is45,46\(\delta (T/{T}_{{{{\rm{c}}}}})=\tanh \{1.821[1.018{({T}_{{{{\rm{c}}}}}/T-1)}^{0.51}]\}\). Here, g(φ) corresponds to the angular dependence of the gap and takes a value of 1 for s-wave and \(| \cos (2\varphi )|\) for d-wave gap symmetry. Motivated by recent studies reporting a nodal-gap structure in CsV3Sb5, evidenced by a non-zero value of the residual linear term of its thermal conductivity at zero field together with its rapid increase with field, we tried to fit the data using a d-wave model29. However, as shown in Fig. 3a and b, a d-wave model cannot describe the data well. On the contrary, recent tunneling experiments27, tunnel-diode oscillator (TDO) based results, along with specific heat measurements conjointly indicate a multiband nature of superconductivity in CsV3Sb528. Thus, we proceeded to fit the \({\lambda }_{{{{\rm{c}}}}}^{-2}(T)\) and \({\lambda }_{{{{\rm{ab}}}}}^{-2}(T)\) data simultaneously with a two-gap scenario using a weighted sum:
Here x is the weight associated with the larger gap and Δ0,i (i = 1, 2 are the band indices) are the gaps related to the first and second band.
The fit of λab(T) and λc(T) with a two-gap (s + s)-wave model was performed by assuming similar gap values [Δ1(2),ab = Δ1(2),c], but different weighting factors for the two directions (xab ≠ xc). A fit with a d-wave model was also performed by considering a similar gap value along two different directions. It is evident that the two-gap model follows the experimental data very well [Fig. 3a and b]. Table 1 summarizes the different superconducting parameters as obtained from the fits. Note that the TF-μSR measurements are well described by gap values which are very close to those obtained from tunneling measurements (Δ1 = 0.57 meV, Δ2 = 0.3 meV, Δ3 = 0.45 meV)27. On the other hand, as shown in Fig. 3a and b, a d-wave model does not describe the data well. This conclusion could be reinforced also by the systematically larger value of the reduced \({\chi }_{r}^{2}\) in case of a d-wave model (1.32) compared to the s + s-wave model fit (1.20). In this regard, it is worthwhile mentioning that recent NMR studies on CsV3Sb5 clearly indicate a coherence peak below Tc47, further supporting nodeless superconductivity in CsV3Sb5. Although thermal conductivity measurements at ultralow temperatures29 suggest the presence of nodes in the superconducting energy gap, our data do not seem to be consistent with with nodal superconductivity, a result further confirmed by NMR/NQR47, tunneling27, specific heat, and magnetic penetration depth based on TDO measurements28. Further studies are needed in order to clarify the discrepancy between the macroscopic and local-probe techniques.
Furthermore, we determined the anisotropy of the magnetic penetration depth, γλ, defined as:
By using the \({\lambda }_{{{{\rm{ab}}}}}^{-2}(T)\) and \({\lambda }_{{{{\rm{c}}}}}^{-2}(T)\) values, we obtain the temperature dependence of the magnetic penetration depth anisotropy as presented in Fig. 3c. According to the phenomenological Ginzburg-Landau theory for uniaxial anisotropic superconductors, the various anisotropies, such as the magnetic penetration depth anisotropy γλ and the upper critical field anisotropy \({\gamma }_{{B}_{{{{\rm{c}}}}2}}\), can be accounted for by a common parameter:48,49
In the above equation, ξ represents the coherence length. In order to compare γλ and \({\gamma }_{{B}_{{{{\rm{c}}}}2}}\), we analyzed the electrical transport data in the presence of various applied fields and estimated the temperature dependence of the upper critical field anisotropy \({\gamma }_{{B}_{{{{\rm{c}}}}2}}(T)\) = Bc2,ab(T)/Bc2,c(T), where Bc2,ab(T) and Bc2,c(T) are the upper critical fields corresponding to zero values of resistivity for B∥ab and B∥c (see Supplementary Fig. 1). Figure 3c depicts also the temperature dependence of \({\gamma }_{{B}_{{{{\rm{c}}}}2}}\). Interestingly, γλ(T) changes slightly from γλ ≃ 1.6 close to Tc to γλ ≃ 3.3 close to T = 0 K. Conversely, \({\gamma }_{{B}_{{{{\rm{c}}}}2}}(T)\) varies strongly from \({\gamma }_{{B}_{{{{\rm{c}}}}2}}\simeq 7.1\) close to Tc to \({\gamma }_{{B}_{{{{\rm{c}}}}2}}\simeq 8.5\) when Tc ≃ 0.3 K.
ZF-μSR experiment in the superconducting state
Finally, to check whether superconductivity breaks time-reversal symmetry in CsV3Sb5, we performed zero-field (ZF) μSR measurements at different temperatures across Tc. A time-reversal symmetry-breaking superconducting state is one of the hallmarks of certain unconventional superconductors; in particular, in many Re-based superconductors50, Sr2RuO451,52,53, Ba1−xKxFe2As254, LaNiC255, La7Ir356 etc. Due to the high muon sensitivity to low magnetic fields, μSR has been the technique of choice for studying it. Here, the ZF-μSR spectra are well described by a damped Gaussian Kubo-Toyabe depolarization function57 (see Supp. Mater. for a detailed description of analysis), which considers the field distribution at the muon site created by both nuclear and electronic moments. The (ZF) μSR experiments were carried out with the muon spin rotated by ~43∘ with respect to the direction of muon momentum. This configuration allows us to use two different detector pairs, namely, Forward(F)- Backward(B) and Left(L)-Right(R), to probe the anisotropic ZF response (see Supplementary Fig. 2 for a schematic view of the experimental geometry). Figure 4a and b shows the ZF-μSR spectra collected above and below Tc. Figure 4c shows the temperature dependence of the electronic relaxation rates for different detectors. The shaded regions represent the statistical scattering of data points. It is evident from Fig. 4c that the relaxation rates do not show any noticeable increase below Tc, indicating that superconductivity does not break TRS in CsV3Sb5 within the statistical accuracy, similar to the recent results on the related system KV3Sb525. Further ZF experiments with high statistics would be interesting in order to confirm or disprove the presence of time reversal symmetry breaking in the superconducting ground state.
a and b ZF-μSR spectra above and below Tc collected in zero field with the initial muon spin polarization being Sμ(0)∣∣ab and Sμ(0)∣∣c, respectively. The solid lines through the spectra are fits as described in the text. c The resulting ZF exponential relaxation rates Λ(T) are almost independent of temperature, thus indicating a preserved TRS. The error bars represent the SD of the fit parameters.
DISCUSSION
The probability field distribution determined experimentally shows a highly asymmetric lineshape, indicative of a well-ordered FLL in the vortex state of the superconductor CsV3Sb5, and it remains almost independent of temperature until very close to Tc. This observation unambiguously suggests that the FLL in CsV3Sb5 is well arranged in the superconducting state and it gets slightly distorted only in the vicinity of Tc. In general, the change of αsk as a function of magnetic field and temperature is associated with the vortex lattice melting40,41,58, and/or a dimensional crossover from a three-dimensional (3D) to a two-dimensional (2D) type of FLL39,41. Both processes are thermally activated and caused by increased vortex mobility via a loosening of the inter- or intraplanar FLL correlations39. Another possibility involves the rearrangement of the vortex lattice induced by a change of the anisotropy coefficient γλ = λc/λab59. Since CsV3Sb5 has a very small superconducting anisotropy (γλ ≃ 3, see below), we can rule out a possible vortex-melting scenario. As for the anisotropy-induced FLL rearrangement, the temperature evolution of αsk measured in Bext∥ab and Bext∥c experiments are expected to be very much different59, which is also not the case here [see Fig. 3c]. Therefore, we are left with the explanation that close to Tc, where the broadening of μSR signal caused by formation of FLL becomes comparable with or even smaller than the relaxation caused by the nuclear magnetic moments [straight lines in Fig. 2e], the shape of P(B) distribution is dominated by the symmetric ‘nuclear’ term, which effectively pushes αsk to zero shortly before the superconducting transition temperature Tc is reached.
Furthermore, a detailed analysis of the λ(T) data reveals the presence of two superconducting gaps at the Fermi surface, with gap values of 0.6 and 0.23 meV. This conclusion is in agreement with recent reports involving different experimental techniques28,60. As μSR is a bulk probe, we conclude that the bulk superconducting gap of this compound consists of two s-wave gaps rather than a nodal gap. Another interesting observation is the fact that the Tc/λ−2(0) ratio for CsV3Sb5 in both field orientations is comparable to those of high-temperature unconventional superconductors and iron-pnictides61,62. Systems with a small Tc/λ−2(0) ~ 0.00025–0.015 are usually considered to be BCS-like, while large Tc/λ−2(0) values are expected only in the BEC-like picture and is considered a hallmark feature of unconventional superconductivity. This approach has become a key feature to characterize BCS-like (so-called conventional) and BEC-like superconductors. Remarkably, in CsV3Sb5, Tc/λ−2(0) is as high as ~ 0.2 (for \({\lambda }_{{{{\rm{ab}}}}}^{-2}(0)\)) - 2.2 (\({\lambda }_{{{{\rm{c}}}}}^{-2}(0)\)), where the lower limit is comparable to the unconventional transition metal dichalcogenide superconductors63 and the upper limit is close to Tc/λ−2(0) ~ 4 of hole-doped cuprates61,62,64. This point towards an unconventional pairing mechanism in the kagome superconductor CsV3Sb5.
Moreover, we observe a clear difference in the temperature dependence of the anisotropies related to magnetic penetration depth and upper critical fields, again signaling a clear deviation from the Ginzburg-Landau theory. This situation finds a clear parallel with the data from the well-known two-gap superconductor MgB265,66, Fe-based Sm- and Nd-1111 systems67,68, 122 pnictide superconductors: Ba(Fe1−xCox)2As269,70, (Ba1−xKx)Fe2As259; FeSe0.5Te0.571, CaKFe4As472, etc., where two different temperature variations of γλ(T) and \({\gamma }_{{B}_{{{{\rm{c}}}}2}}(T)\) were attributed to multiband superconductivity. Thus, in comparison to well-established multigap superconductors, we find further support for the multigap behavior in this compound. Therefore, our results provide microscopic evidence of anisotropic multigap superconductivity in the kagome superconductor CsV3Sb5 and encourage further theoretical and experimental research on the kagome superconductors.
Finally, ZF-μSR experiments suggest that across Tc, the relaxation rates do not change. This suggests that within the statistical accuracy, no clear signature of TRS breaking is observed in the superconducting state of CsV3Sb5.
METHODS
Sample preparation
Single crystals of CsV3Sb5 were grown from Cs ingots (purity 99.9%), V 3-N powder (purity 99.9%) and Sb grains (purity 99.999%) using the self-flux method, similar to the growth of RbV3Sb573. The eutectic mixture of CsSb and CsSb2 was mixed with VSb2 to form a composition with approximately 50 at% CsxSby and 50 at% VSb2. The mixture was put into an alumina crucible and sealed in a quartz ampoule under partial argon atmosphere. The sealed quartz ampoule was heated to 1273 K in 12 h and kept there for 24 h. Then it was cooled down to 1173 K at 50 K/h and further to 923 K at a slower rate. Finally, the ampoule was removed from the furnace and decanted with a centrifuge to separate the CsV3Sb5 crystals from the flux. The obtained crystals have a typical size of 4 × 4 × 1 mm3 and are stable in air over a period of at least several months. As shown in Fig. 1a and b, the flux-grown single crystals possess an obvious hexagonal symmetry, while the X-ray Laue diffraction images demonstrate the single crystallinity of the material. The XRD pattern was collected using a Bruker D8 x-ray diffractometer with Cu Kα radiation (λ = 0.15418 nm) at room temperature.
Magnetic susceptibility and electrical transport measurements
The magnetization measurements were performed in a Quantum Design magnetic property measurement system SQUID magnetometer under field-cooled and zero-field-cooled conditions. Electrical transport measurements were carried out in a Quantum Design physical property measurement system (PPMS-14T). The longitudinal electrical resistivity was measured using a four-probe method with the current flowing in the ab plane. For measurements in the temperature range 0.3–2 K we employed a Heliox recondensing He-3 system, which is equipped with a superconducting NbTi twisted pair cable for the measurements.
μSR-experiments
We performed transverse field (TF) and zero field μSR experiments using the Dolly spectrometer (πE1 beamline) at the Paul Scherrer Institute (Villigen, Switzerland). Since the crystals were rather thick (~1 mm), they were mounted in a single layer using Apiezon N grease, to form a mosaic covering an area of 7 × 7 mm2. The Dolly spectrometer is equipped with a standard veto setup, providing a low-background μSR signal. All TF- μSR experiments were done after field-cooling the sample with the applied field either along the kagome plane or perpendicular to it. The μSR time spectra were analyzed using the open software package MUSRFIT74.
Notes added
While preparing this manuscript, we came to know about another μSR work studying the high temperature charge ordered phase of CsV3Sb5 [arXiv:2107.10714 (2021) (https://arxiv.org/abs/2107.10714)].
Data availability
The data supporting the findings of this study are available within the paper and in the Supplementary Information. The raw data are available from the corresponding authors upon reasonable request or raw data can also be found at the following link http://musruser.psi.ch/cgi-bin/SearchDB.cgi.
References
Yin, J.-X. et al. Negative flatband magnetism in a spin-orbit coupled kagome magnet. Nat. Phys. 15, 443 (2019).
Guguchia, Z. et al. Tunable anomalous Hall conductivity through volume-wise magnetic competition in a topological kagome magnet. Nat. Commun. 11, 559 (2020).
Ghimire, N. & Mazin, I. Topology and correlations on the kagome lattice. Nat. Mater. 19, 137–138 (2020).
Ye, L. et al. Massive Dirac fermions in a ferromagnetic kagome metal. Nature 555, 638–642 (2018).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Hofmann, J. S., Berg, E. & Chowdhury, D. Superconductivity, pseudogap, and phase separation in topological flat bands. Phys. Rev. B 102, 201112(R) (2020).
Nunes, L. H. C. M. & Smith, C. M. Flat-band superconductivity for tight-binding electrons on a square-octagon lattice. Phys. Rev. B 101, 224514 (2020).
Mielke III, C. et al. Nodeless kagome superconductivity in LaRu3Si2. Phys. Rev. Mat. 5, 034803 (2021).
Ortiz, B. et al. New kagome prototype materials: discovery of KV3Sb5, RbV3Sb5, and CsV3Sb5. Phys. Rev. Mat. 3, 09447 (2019).
Yang, S. et al. Giant, unconventional anomalous Hall effect in the metallic frustrated magnet candidate, KV3Sb5. Sci. Adv. 6, 1–7s (2020).
Yu, F. et al. Concurrence of anomalous Hall effect and charge density wave in a superconducting topological kagome metal. Phys. Rev. B 104, L041103 (2021).
Zhao, H. et al. Cascade of correlated electron states in a kagome superconductor CsV3Sb5. Nature 599, 216–221 (2021).
Fu, Y. et al. Quantum transport evidence of topological band structures of kagome superconductor CsV3Sb5. Phys. Rev. Lett. 127, 207002 (2021).
Jiang, Y.-X. et al. Unconventional chiral charge order in kagome superconductor KV3Sb5. Nat. Mater. 20, 1353–1357 (2021).
Denner, M., Thomale, R. & Neupert., T. Analysis of charge order in the kagome metal AV3Sb5 (A = K, Rb, Cs). Phys. Rev. Lett. 127, 217601 (2021).
Shumiya, N. et al. Intrinsic nature of chiral charge order in the kagome superconductor RbV3Sb5. Phys. Rev. B 104, 035131 (2021).
Wang, Z. et al. Electronic nature of chiral charge order in the kagome superconductor CsV3Sb5. Phys. Rev. B 104, 075148 (2021).
Kang, M. et al. Twofold van Hove singularity and origin of charge order in topological kagome superconductor CsV3Sb5. Nat. Phys. https://doi.org/10.1038/s41567-021-01451-5 (2022).
Li, H. et al. Observation of unconventional charge density wave without acoustic phonon anomaly in kagome superconductors AV3Sb5 (A = Rb, Cs). Phys. Rev. X 11, 031050 (2021).
Song, D. et al. Orbital ordering and fluctuations in a kagome superconductor CsV3Sb5. Sci. China: Phys. Mech. Astron. 65, 247462 (2022).
Ortiz, B. et al. CsV3Sb5: A Z2 topological kagome metal with a superconducting ground state. Phys. Rev. Lett. 125, 247002 (2020).
Ortiz, B. et al. Superconductivity in the Z2 kagome metal KV3Sb5. Phys. Rev. Mater. 5, 034801 (2021).
Yin, Q. et al. Superconductivity and normal-state properties of kagome metal RbV3Sb5 single crystals. Chin. Phys. Lett. 38, 037403 (2021).
Liu, Z. et al. Charge-density-wave-induced bands renormalization and energy gaps in a kagome superconductor RbV3Sb5. Phys. Rev. X 11, 041010 (2021).
Mielke III, C. et al. Time-reversal symmetry-breaking charge order in a correlated kagome superconductor. Nature 602, 245 (2022).
Wang, Y. et al. Proximity-induced spin-triplet superconductivity and edge supercurrent in the topological kagome metal, KV1−xSb5. Preprint at https://arxiv.org/abs/2012.05898 (2020).
Xu, H.-S. et al. Multiband superconductivity with sign-preserving order parameter in kagome superconductor CsV3Sb5. Phys. Rev. Lett. 127, 187004 (2021).
Duan, W. et al. Nodeless superconductivity in the kagome metal CsV3Sb5. Sci. China-Phys. Mech. Astron. 64, 107462 (2021).
Zhao, C. et al. Nodal superconductivity and superconducting domes in the topological kagome metal CsV3Sb5. Preprint at https://arxiv.org/abs/2102.08356 (2021).
Zhang, Z. et al. Pressure-induced reemergence of superconductivity in the topological kagome metal CsV3Sb5. Phys. Rev. B 103, 224513 (2021).
Chen, X. et al. Highly-robust reentrant superconductivity in CsV3Sb5 under pressure. Chin. Phys. Lett. 38, 057402 (2021).
Chen, K. et al. Double superconducting dome and triple enhancement of Tc in the kagome superconductor CsV3Sb5 under high pressure. Phys. Rev. Lett. 126, 247001 (2021).
Wu, X. et al. Nature of unconventional pairing in the kagome superconductors AV3Sb5 (A = K, Rb, Cs). Phys. Rev. Lett. 127, 177001 (2021).
Kiesel, M. L. & Thomale, R. Sublattice interference in the kagome Hubbard model. Phys. Rev. B 86, 121105 (2012).
Sonier, J. E., Brewer, J. H. & Kiefl, R. F. μSR studies of the vortex state in type-II superconductors. Rev. Mod. Phys. 72, 769 (2000).
Ouladdiaf, B. et al. OrientExpress: a new system for Laue neutron diffraction. Phys. B: Condens. Matter. 385-386, 1052 (2006).
Maisuradze, A., Khasanov, R., Shengelaya, A. & Keller, A. Comparison of different methods for analyzing μSR line shapes in the vortex state of type-II superconductors. J. Phys.: Condens. Matter 21, 075701 (2009).
Thiemann, S., Radović, Z. & Kogan, V. Field structure of vortex lattices in uniaxial superconductors. Phys. Rev. B 39, 11406 (1989).
Aegerter, C. et al. Angular dependence of the disorder crossover in the vortex lattice of Bi2.15Sr1.85CaCu2O8+δ by muon spin rotation and torque magnetometry. Phys. Rev. B 57, 1253 (1998).
Lee, S. et al. Evidence for flux-lattice melting and a dimensional crossover in single-crystal Bi2.15Sr1.85CaCu2O8+δ from muon spin rotation studies. Phys. Rev. Lett. 71, 3862 (1993).
Blasius, T. et al. Evidence for a two-stage melting transition of the vortex matter in Bi2Sr2Ca1Cu2O8+δ single crystals obtained by muon spin rotation. Phys. Rev. Lett. 82, 4926 (1999).
Heron, D. O. G. et al. Muon-spin rotation measurements of an unusual vortex-glass phase in the layered superconductor Bi2.15Sr1.85CaCu2O8+δ. Phys. Rev. Lett. 110, 107004 (2013).
Brandt, E. H. Flux distribution and penetration depth measured by muon spin rotation in high-Tc superconductors. Phys. Rev. B 37, 2349(R) (1988).
Brandt, E. H. Properties of the ideal Ginzburg-Landau vortex lattice. Phys. Rev. B 68, 054506 (2003).
Khasanov, R., Gupta, R., Das, D., Leithe-Jasper, A. & Svanidze, E. Single-gap versus two-gap scenario: Specific heat and thermodynamic critical field of the noncentrosymmetric superconductor BeAu. Phys. Rev. B 102, 014514 (2020).
Carrington, A. & Manzano, F. Magnetic penetration depth of MgB2. Physica C 385, 205 (2003).
Mu, C. et al. S-wave superconductivity in kagome metal CsV3Sb5 revealed by 121/123Sb NQR and 51V NMR measurements. Chin. Phys. Lett. 38, 077402 (2021).
Kogan, V. G. London approach to anisotropic type-II superconductors. Phys. Rev. B 24, 1572 (1981).
Tinkham, M. Introduction to Superconductivity. Krieger Publishing Company, Malabar, Florida, (1975).
Shang, T. & Shiroka, T. Time-reversal symmetry breaking in Re-based superconductors: recent developments. Front. Phys. 9, 270 (2021).
Luke, G. Time-reversal symmetry-breaking superconductivity in Sr2RuO4. Nature 394, 559 (1998).
Grinenko, V. Unsplit superconducting and time reversal symmetry breaking transitions in Sr2RuO4 under hydrostatic pressure and disorder. Nat. Commun. 12, 3920 (2021).
Grinenko, V. Split superconducting and time-reversal symmetry-breaking transitions in Sr2RuO4 under stress. Nat. Phys. 17, 748 (2021).
Grinenko, V. Superconductivity with broken time-reversal symmetry inside a superconducting s-wave state. Nat. Phys. 16, 789 (2020).
Hillier, A. D., Quintanilla, J. & Cywinski, R. Evidence for time-reversal symmetry breaking in the noncentrosymmetric superconductor LaNiC2. Phys. Rev. Lett. 102, 117007 (2009).
Barker, J. A. T. et al. Unconventional superconductivity in La7Ir3 revealed by muon spin relaxation: introducing a new family of noncentrosymmetric superconductor that breaks time-reversal symmetry. Phys. Rev. Lett. 115, 267001 (2015).
Hayano, R. et al. Zero- and low-field spin relaxation studied by positive muons. Phys. Rev. B 20, 850 (1979).
Khasanov, R. et al. Evidence for a competition between the superconducting state and the pseudogap state of (BiPb)2(SrLa)2CuO6+δ from muon spin rotation experiments. Phys. Rev. Lett. 101, 227002 (2008).
Khasanov, R. et al. Two-gap superconductivity in Ba1−xKxFe2As2: A complementary study of the magnetic penetration depth by muon-spin rotation and angle-resolved photoemission. Phys. Rev. Lett. 102, 187005 (2009).
Ni, S. et al. Anisotropic superconducting properties of kagome metal CsV3Sb5. Chin. Phys. Lett. 38, 057403 (2021).
Uemura, Y. et al. Universal correlations between Tc and ns/m (carrier density over effective mass) in high-Tc cuprate superconductors. Phys. Rev. Lett. 62, 2317 (1989).
Uemura, Y. et al. Basic similarities among cuprate, bismuthate, organic, Chevrel-phase, and heavy-fermion superconductors shown by penetration-depth measurements. Phys. Rev. Lett. 66, 2665 (1991).
Guguchia, Z. et al. Signatures of the topological s+− superconducting order parameter in the type-II weyl semimetal Td-MoTe2. Nat. Comm. 8, 1082 (2017).
Gupta, R., Ying, T. P., Qi, Y. P., Hosono, H. & Khasanov, R. Gap symmetry of the noncentrosymmetric superconductor W3Al2C. Phys. Rev. B 103, 174511 (2021).
Angst, M. et al. Temperature and field dependence of the anisotropy of MgB2. Phys. Rev. Lett. 88, 167004 (2002).
Fletcher, J. D., Carrington, A., Taylor, O. J., Kazakov, S. M. & Karpinski, J. Temperature-dependent anisotropy of the penetration depth and coherence length of MgB2. Phys. Rev. Lett. 95, 097005 (2005).
Weyeneth, S. et al. Evidence for two dstinct anisotropies in the oxypnictide superconductors SmFeAsO0.8F0.2 and NdFeAsO0.8F0.2. Supercond. Nov. Magn. 22, 347–351 (2009).
Gupta, R. et al. Self-consistent two-gap approach in studying multi-band superconductivity of NdFeAsO0.65F0.35. Front. Phys. 8, 2 (2020).
Prozorov, R. Anisotropic London penetration depth and superfluid density in single crystals of iron-based pnictide superconductors. Physica C 469, 582–589 (2009).
Tanatar, M. A. et al. Anisotropy of the iron pnictide superconductor Ba(Fe1−xCox)2As2 (x = 0.074, Tc = 23 K). Phys. Rev. B 79, 094507 (2009).
Bendele, M. et al. Anisotropic superconducting properties of single-crystalline FeSe0.5Te0.5. Phys. Rev. B 81, 224520 (2010).
Khasanov, R. et al. Anisotropy induced vortex lattice rearrangement in CaKFe4As4. Phys. Rev. B 99, 140507(R) (2019).
Yin, Q. W. et al. Superconductivity and normal-state properties of kagome metal RbV3Sb5 single crystals. Chin. Phys. Lett. 38, 037403 (2021).
Suter, A. & Wojek, B. M. Musrfit: a free platform-independent framework for μSR data analysis. Phys. Procedia 30, 69 (2012).
Yaouanc, A., Dalmas de Reotier, P. & Brandt, E. H. Effect of the vortex core on the magnetic field in hard superconductors. Phys. Rev. B 55, 11107 (1997).
Acknowledgements
μSR experiments were performed at the Swiss Muon Source (SμS), Paul Scherrer Institute (PSI), Switzerland. The work of RG was supported by the Swiss National Science Foundation (SNF-Grant No. 200021-175935). H.C.L. was supported by National Natural Science Foundation of China (Grant Nos. 11822412 and 11774423), Ministry of Science and Technology of China (Grant Nos. 2018YFE0202600 and 2016YFA0300504) and the Beijing Natural Science Foundation (Grant No. Z200005).
Author information
Authors and Affiliations
Contributions
R.G., D.D., and C.M. contributed equally to this work. R.G., D.D., C.M., Z.G., R.K., and C.B. carried out μSR experiments. R.G., D.D., C.M., and R.K. performed μSR data analysis. Q.Y., Z.T., C.G., and H.C.L. provided and characterized samples. M.B. performed low temperature electrical transport measurements under different fields. H.L. supervised the work at PSI. R.G., D.D., C.M., Z.G., and T.S. prepared the manuscript with notable inputs from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gupta, R., Das, D., Mielke III, C.H. et al. Microscopic evidence for anisotropic multigap superconductivity in the CsV3Sb5 kagome superconductor. npj Quantum Mater. 7, 49 (2022). https://doi.org/10.1038/s41535-022-00453-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-022-00453-7
This article is cited by
-
Enhancement of superconductivity and phase diagram of Ta-doped Kagome superconductor CsV3Sb5
Scientific Reports (2024)
-
Conventional superconductivity in the doped kagome superconductor Cs(V0.86Ta0.14)3Sb5 from vortex lattice studies
Nature Communications (2024)
-
Evidence of a distinct collective mode in Kagome superconductors
Nature Communications (2024)
-
AV3Sb5 kagome superconductors
Nature Reviews Materials (2024)
-
Bulk evidence of anisotropic s-wave pairing with no sign change in the kagome superconductor CsV3Sb5
Nature Communications (2023)