Abstract
Two-dimensional SrTiO3-based interfaces stand out among non-centrosymmetric superconductors due to their intricate interplay of gate-tunable Rashba spin-orbit coupling and multi-orbital electronic occupations, whose combination theoretically prefigures various forms of non-standard superconductivity. By employing superconducting transport measurements in nano-devices we present strong experimental indications of unconventional superconductivity in the LaAlO3/SrTiO3 interface. The central observations are the substantial anomalous enhancement of the critical current by small magnetic fields applied perpendicularly to the plane of electron motion, and the asymmetric response with respect to the magnetic field direction. These features cannot be accommodated within a scenario of canonical spin-singlet superconductivity. We demonstrate that the experimental observations can be described by a theoretical model based on the coexistence of Josephson channels with intrinsic phase shifts. Our results exclude a time-reversal symmetry breaking scenario and suggest the presence of anomalous pairing components that are compatible with inversion symmetry breaking and multi-orbital physics.
Similar content being viewed by others
Introduction
Accessing the fundamental structure of Cooper pairs in unconventional superconductors1 and the mechanisms behind electron pairing are among the most notable challenges in condensed matter physics. A superconductor exhibits unconventional pairing when one has breaking of either time-reversal or inversion symmetries apart from the canonical gauge symmetry. Two-dimensional (2D) superconductors offer new opportunities to study and tailor unconventional superconducting order parameters as they inherently lack inversion symmetry in the presence of Rashba-type spin-orbit coupling and allow large electrostatic tuning of charge carrier density and bands occupation2,3,4,5. The 2D electron systems in SrTiO3 based heterostructures, such as LaAlO3/SrTiO3 (LAO/STO)6,7, are a versatile platform for studying non-centrosymmetric multi-orbital superconductivity8,9,10 due to the ability to modulate by electrostatic gating the superconducting critical temperature11,12,13 together with the strength of the Rashba spin-orbit coupling14,15 and the occupation of the Ti 3d orbitals (dxy,dxz,dyz)16,17. Remarkably, the combination of inversion symmetry breaking and multiple orbital degrees of freedom can yield a superconducting order parameter that goes beyond the canonical singlet-triplet mixed parity, with an inter-band anti-phase pairing (e.g., s+−)9 or pure even-parity inter-orbital spin-triplet pairs8. Recently, several experimental observations have been considered as a direct manifestation of an s+− pairing or as a generic indication of an unconventional type of superconductivity. Notable examples are the observation of a superconducting gap suppression nearby a Lifshitz transition18,19, the anomalous magnetic field dependence of critical current in weak links20,21 and uniform nanowires22, and several in-gap bound states probed by tunneling spectroscopy23.
In addition, there are also definite indications of intrinsic inhomogeneities in the normal24,25 and superconducting26,27,28 states of the LAO/STO interface originating either from structural domains or electronic phase separation29. Therefore, the superconducting phase is likely to be marked by nonuniform superconducting islands28,30,31. While these strong nonmagnetic inhomogeneities, at first sight, can be incompatible with an unconventional type of pairing, it has been recently figured out that extra internal degrees of freedom such as orbitals, sublattices, or valleys can protect Cooper pairs from strong scattering32. Then, local inter-band anti-phase pairing or inter-orbital spin-triplet states are not precluded and can provide robust features of interference effects even in inhomogeneous superconducting conditions. The overall scenario underlines fundamental challenges not yet fully settled about the unconventional nature of the superconducting state in LAO/STO interface, its interrelation with the multi-orbital degrees of freedom, the survival in a strongly inhomogeneous environment, as well as the eventual occurrence of extra symmetry breaking.
In this work, we performed a detailed investigation of the superconducting transport in the LAO/STO nano-devices as a function of magnetic field and gate voltage. The main finding is a very strong anomalous enhancement of critical current (Ic) in a small perpendicular magnetic field (B⊥). The effect is significantly enhanced at positive gate voltages corresponding to the regime of multiband occupation. This anomalous magnetic field dependence of critical current cannot be explained by classical models of s-wave superconductivity. We propose a phenomenological model based on a multiband non-centrosymmetric superconductor in which the enhancement of the critical current is explained as an interference effect of Josephson channels with intrinsic phase shifts. The symmetry of Ic(B⊥) response excludes the time-reversal symmetry breaking mechanism for the occurrence of unconventional pairing components. We show that inversion symmetry breaking and non-trivial multi-orbital superconductivity are sufficient to account for the experimental observations and gate tunability of the effect.
Results and discussion
Device geometry and I–V characteristics
The devices in this study are bridges with a width of 1 μm that contain artificially created weak links with a barrier length of 35 nm, see Fig. 1a. Devices were patterned in 5uc-LaAlO3 thin films deposited on TiO2 terminated (001)-SrTiO3 substrates using double-step electron-beam lithography (EBL) and low energy ion irradiation technique, see Methods section. To create the weak links, we utilized the unique property of Ar+ ion irradiation that allows gradual tuning of interface resistance33,34.
a Schematic of the LaAlO3/SrTiO3 device fabricated using double-step electron-beam lithography and low energy Ar+ ion irradiation. The upper surface of the schematic represents the actual atomic force microscopy topographic scan of the device. The dark red region represents the conducting interface, while the light (pink) area corresponds to the insulating interface. The W ~ 1 μm (here) denotes the width of the conducting channel. The upper panel shows a magnified view of the weak link region in the middle of the device with a weak link length L ~ 35 nm. Scale bar, 200 nm. The right panel shows a schematic of the crystal structure of the LaAlO3/SrTiO3 heterointerface. b Sketch of the band structure of the 2DEG, adapted from ref. 10. c Current I vs voltage V traces at different gate voltage Vg measured at 20 mK in a four-probe configuration. d Gate voltage-dependent color plot of dV/dI. e Normalized resistance vs gate voltage curves obtained from the fitting of the linear region of I–V curves measured in two different geometries presented in the inset. The green curve is the measured resistance using a four-probe method where current flows through the weak link, while red data are obtained in a two-probe configuration where the weak link is excluded.
The properties of the weak links were first investigated by measurements of their I–V characteristics at T = 20 mK and different gate voltages (Vg) applied at the backside of the SrTiO3 substrate (Fig. 1c). The I–V characteristics were obtained by measuring voltage drop in a four-terminal configuration across the bridge. There is an apparent hysteresis in the I–V characteristics at high gate voltages characterized by the presence of high critical current, Ic, and small return current, Icr. This hysteresis in nanowires is often attributed to Joule heating22,35. The critical current Ic decreases non-monotonically with reducing the back-gate voltage from 11 to 7.2 V (Fig. 1d) due to the loss of superconducting phase coherence. At the same time, the return current is gate voltage-independent that further supports its thermal origin. The weak links are clearly discerned from the uniform bridges by their increased normal resistance (Fig. 1e) and much faster decay of critical current as a function of the gate voltage (Supplementary Fig. S7). This implies that the transparency of our artificial weak link is reduced faster as compared to one of the electrodes.
Magnetic field dependence of critical current
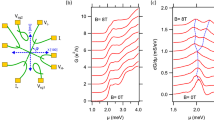
Next, we present the effect of the applied out-of-plane magnetic field (B⊥) on the critical current. The magnetic field normally suppresses the critical current due to the pair breaking caused by orbital or paramagnetic effects. In contrast, we observe a substantial enhancement of critical current Ic as soon as a small B⊥ is applied (Fig. 2a). The Ic increases from ~35 nA at 0 mT to ~90 nA at +2 mT and then shows a gradual reduction for further increase of B⊥. Plotting dV/dI as a function of B⊥ and current reveals a striking asymmetric dependence of Ic as a function of the direction of B⊥ (Fig. 2b). The asymmetry results in different amplitudes of positive (\({I}_{c}^{+}\)) and negative (\({I}_{c}^{-}\)) values of critical current at a finite magnetic field. However, the magnetic field pattern is symmetric with respect to the change of sign of both critical current and magnetic field, i.e., \({I}_{c}^{+}({B}_{\perp })=-{I}_{c}^{-}(-{B}_{\perp })\), indicating the absence of time-reversal symmetry breaking.
a Selected current I vs voltage V traces of the device measured at 11 V, and 20 mK as a function of the magnetic field, in the range of ±5 mT, applied perpendicular to the plane of the sample. The curves are shifted horizontally for clarity. A background color highlights critical current variation with B⊥. b Contour plot of dV/dI as a function of the current and the out-of-plane magnetic field. c Selective I–V traces measured at 11 V, and 20 mK as a function of the in-plane magnetic field applied the range of ±25 mT. d Contour plot of dV/dI as a function of the current and the in-plane magnetic field.
We also note that the effect is observed only when the magnetic field is applied perpendicularly to the plane, whereas there is no enhancement of Ic in the parallel magnetic field (B∥) as shown in Fig. 2c, d. Meanwhile, the normal resistance does not show a magnetic field dependence similar to that of Ic(B⊥), see Supplementary Fig. S13, indicating that the effect is due to the enhancement of superconducting current. There is also negligible hysteresis in Ic(B⊥) dependence that rules out the presence of intrinsic magnetism in our samples, in contrast with earlier reports where very strong hysteresis in magnetoresistance was observed36.
An identical enhancement of Ic between 0 and 2 mT is also observed in uniform bridges without artificial weak link (Supplementary Fig. S8), but with a relatively large maximum critical current, Ic(2 mT)~130 nA, and also a clear asymmetric response as a function of the B⊥ direction. This is in agreement with the presence of intrinsic weak links in the interface27,28,29. The artificial weak link allows much more effective tunability of barrier transparency as a function of gate voltage as compared with electrodes and thus serves as a better probe of the order parameter. The effect of Ic enhancement as a function of B⊥ is strongly suppressed as Vg is reduced and completely disappears below 7.5 V, see Fig. 3a–h. In Fig. 4a, we compare Ic as a function of the gate voltage estimated at the minimum (B⊥ = 0 mT) and maximum (B⊥ = 2 mT) of Ic obtained from the curves in Fig. 3. It is readily apparent that the Ic(2 mT) shows more rapid suppression with Vg in comparison to smooth reduction at 0 mT, see also Supplementary Fig. S9 for the evolution of Ic with Vg of the uniform bridge. There is also a sign reversal in asymmetry with respect to the magnetic field direction at ~9.5 V, as evident from Fig. 4b, where we show the normalized positive critical current as a function of B⊥ at different Vg. In Fig. 4c, \({{\Delta }}{I}_{n}={I}_{n}^{+}(2\ \,{{\mbox{mT}}}\,)-{I}_{n}^{-}(-2\ \,{{\mbox{mT}}}\,)\) is plotted as a function of Vg, where \({I}_{n}^{+}({I}_{n}^{-})\) represents the value of normalized positive critical current at 2 mT (−2 mT), which exhibits a transition from positive to negative values at 9.5 V. We performed similar Ic(B⊥) measurements in the gate voltage range of 11 to −2 V for uniform bridges, as shown in Supplementary Fig. S9. The result, in this case, does not exhibit a clear sign change in the asymmetry of Ic(B⊥). Therefore, the behavior of the gate-tunable sign change in the asymmetry of Ic(B⊥) is more evident in the artificial weak link.
a The evolution of the critical current estimated at constant magnetic fields 0 and +2 mT, with gate voltages between 11 and 7.5 V. b The normalized positive critical current \({I}_{c}^{+}(B)/{I}_{c}^{+}(0)\)vs B⊥ estimated from I–V vs B curves at different gate voltages. The dashed lines represent the value of current (In) at ±2 mT. c The variation of \({{\Delta }}{I}_{n}={I}_{n}^{+}(2\ \,{{\mbox{mT}}}\,)-{I}_{n}^{-}(-2\ \,{{\mbox{mT}}}\,)\) as a function of Vg. A clear crossing of the zero line takes place and this indicates the sign reversal at ~9.5 V. d Illustration of the three-channel theoretical model, where the total width is W = W1 + W2 + W3, with corresponding intrinsic phase drop of φin = 0, π, and φ0. e, f Magnetic flux dependence of the normalized critical current \({I}_{c}^{{\varphi }_{0}}({{\Phi }})/{I}_{c}^{\,{{\mbox{min}}}\,}\) (where \({I}_{c}^{\,{{\mbox{min}}}}={{\mbox{min}}}\,\left[{I}_{c}^{{\varphi }_{0}}({{\Phi }} \sim 0)\right]\)) at fixed i3 = 0.05 and 1.5 and different values of i2, and equal channel widths, W1 = W2 = W3 = W/3. Here, i2 = I20/I10 and i3 = I30/I10 indicate the ratios between the weights of the channels π and 0 and between the channels φ0 and 0, respectively. g The variation of ΔIc as a function of i2 and i3. Here, \({{\Delta }}{I}_{c}=\max \left[{I}_{c}^{{\varphi }_{0}}({{\Phi }}\, > \,0)\right]-\max \left[{I}_{c}^{{\varphi }_{0}}({{\Phi }}\, < \,0)\right]\). h The ratio \({{{{{\mathcal{R}}}}}}\) of maximum/minimum of \({I}_{c}^{{\varphi }_{0}}({{\Phi }})\) as a function of (i2, i3). i The variation of ΔIc as a function of i2 at different values of i3.
Conventional superconductivity mechanisms of critical current enhancement
The critical question to start with is whether the observed enhancement of Ic can be understood within classical superconductivity frameworks, or one needs to invoke scenarios with unconventional pairing. There are various effects proposed earlier to explain the anomalous enhancement of the critical current by magnetic fields, such as those due to an internal compensation of intrinsic exchange fields by the external magnetic field37. This mechanism however is also expected to enhance the critical temperature as a function of the applied magnetic field, as observed in the previous reports38. To evaluate this compensation mechanism, we have measured the I–Vs as a function of B⊥ at different temperatures below the critical temperature, and resistance vs temperature curves at different constant B⊥ in the vicinity of the superconducting transition. In Supplementary Fig. S6a–h, we show the I–V(B⊥) measured at different temperatures and at 11 V. The amplitude of Ic enhancement reduces with increasing the temperature and disappears above 70 mK, much below the critical temperature of the device. In addition, the critical temperature estimated from R(T) measurements (Supplementary Fig. S6i) displays a linear decrease with the B⊥ (Supplementary Fig. S6j). Thus, this scenario is incompatible with our results, which only display a pronounced effect at the lowest temperature below the superconducting transition (Tc ~ 105 mK). We can also rule out the effect of suppression of spin-flip scattering on magnetic impurities39 as it is expected to be enhanced when the magnetic field is aligned parallel to the interface40,41, which is not consistent with our experimental results, see Fig. 2c, d.
The normal resistance, as shown in Supplementary Fig. S13, does not depend on the magnetic field and thus cannot be the reason for the observed enhancement of Ic, as reported earlier in small magnetic fields42,43. Non-equilibrium quasiparticle poisoning has recently been discussed in relation to the enhancement of Ic, which is a result of increased thermalization of hot quasiparticles due to the softening of the superconducting gap by a magnetic field44. The thermalization effect in nanowires is expected to be much stronger in narrower structures due to limited electron-phonon cooling power45. To address this issue, we measured two different kinds of uniform devices: single-connected (Supplementary Fig. S10a) and double-connected (rings) (Supplementary Fig. S10b), with different widths in the range of W = 0.1–1 μm for planar devices and W = 0.1–0.3 μm for ring structures. We see a systematic reduction of the amplitude of Ic enhancement with reducing the width of the devices both for planar and ring-shaped devices. This confirms that the quasiparticle heating cannot account for the Ic enhancement. Moreover, the re-trapping current shows no increase with B⊥, excluding thermalization effects as a mechanism responsible for our observations44 (Supplementary Fig. S11).
Unconventional pairing channels with intrinsic phase shifts
A completely different and more fundamental view of the enhancement of critical current by the small perpendicular magnetic field is based on the interference of supercurrents flowing in channels with intrinsic phase shifts46. In general, a non-trivial phase relation of the superconducting order parameter appears when time or inversion symmetry is broken47,48,49,50. On the basis of symmetry arguments and considering the electronic structure of the LAO/STO interface, two physical scenarios emerge as the most relevant and plausible. The LAO/STO is a quasi-2D non-centrosymmetric superconductor and, due to confinement and electrostatic gating, the electronic structure is governed by strong inversion asymmetry. On the other hand, there have been experimental reports indicating the presence of ferromagnetic ordering at the LAO/STO interface co-existing with superconductivity providing an explicit source of time-reversal symmetry breaking26. Both these types of symmetries breaking may support anomalous Josephson channels in the superconducting phase. Furthermore, a key aspect of the LAO/STO interface is given by the presence of multi-orbital degrees of freedom that hints for having more than one channel with different phase shifts, which in turn can be tuned by the applied gate voltage. Due to the symmetry of the critical current by reversing the sign of both I and B⊥ (\({I}_{c}^{+}({B}_{\perp })=-{I}_{c}^{-}(-{B}_{\perp })\)) and no experimental evidence of the presence of significant hysteresis in Ic − B and Rn − B (see Supplementary Fig. S13), the time-reversal symmetry breaking is unlikely to occur in the LAO/STO interface. Therefore, we will focus on a model in which the inversion symmetry breaking is the primary source of an unconventional superconducting state associated with anomalous magnetic field dependence of the critical current. Here, the main challenge is to understand whether the experimental features can be accounted for within this scenario in a way that it is not much sensitive to the fine-tuning of the model parameters.
In order to explain both the presence of a minimum of critical current at zero magnetic field, and a sign tunable asymmetry of Ic(H), we propose a model assuming that the resulting zero magnetic field critical current across the weak link is a superposition of three current channels having intrinsic phase drops with φin = 0, π, and a φ0 contributions, see Fig. 4d. Thus, the constituting currents can be expressed as follows: \({I}_{1}={I}_{10}\sin (\varphi )\), \({I}_{2}={I}_{20}\sin (\varphi +\pi )\), and \({I}_{3}={I}_{30}[\sin (\varphi )+\gamma \sin (2\varphi )]\). It is crucial that γ is negative and has an amplitude relation that allows having a minimum of the Josephson energy at a non-zero phase bias φ0 (details are reported in the Supplementary information). This phase state is time-reversal invariant (i.e., there is no spontaneous current flow at φ = 0), and the contributions can be deduced by assuming a multiband non-centrosymmetric superconductor with the combination of singlet and triplet pairs, thus stemming only on the role played by inversion symmetry breaking and multi-orbital degrees of freedom. The application of an external magnetic field modulates the amplitude of supercurrent as expected in a conventional Josephson junction. Assuming a junction of length L and width W, the magnetic field dependence of the current for a given channel can be expressed as \(I(H,\varphi )=JL\int\nolimits_{0}^{W}\sin (2\pi \frac{HLx}{{{{\Phi }}}_{0}}+\varphi +{\varphi }_{in})dx\), with J being the current density and Φ0 = h/2e the unit of flux quantum. The critical current can be determined by summing up the contributions from all channels and maximizing the result with respect to the phase φ. The results of the calculations are presented in Fig. 4e–i. The model is successfully capturing the following experimental key features qualitatively: (i) the maximum of the Ic that occurs at a non-zero value of the B⊥ as shown in Fig. 4e, f, (ii) the minimum of Ic at about B⊥ = 0, (iii) the absence of parity in the pattern Ic vs B⊥, i.e., by reversing the direction of the magnetic field (B → −B) the critical current is not symmetric (Fig. 4e), and finally (iv) the sign of the Ic − B⊥ asymmetry, expressed through the difference between the Ic at positive and negative applied field B⊥, that can be reversed by applying an external gate voltage (Fig. 4f, g). Remarkably, the presence of the φ0 channel is necessary to obtain the asymmetry and overall current-field profile, even without the fine-tuning of the size of the regions corresponding to the 0, π, and φ0 channels. This implies that the result does not depend on the junction’s geometry and the relative width of the supercurrent channels. The presence of local disorders such as oxygen vacancies and ferroelectric domains will not modify the intrinsic phase shifts in the system but may change the amplitude and distribution of different channels through the nanowire and the overall effect on the characteristics of the critical current would remain unchanged qualitatively. Moreover, even quantitative matching between the model and experiment may be improved due to the presence of extra fitting parameters associated with the multiple channels.
Concerning the origin of the Josephson components, the gate tunability of the supercurrent patterns clearly points to a substantial role of the orbital degrees of freedom in setting out a non-trivial pairing structure. The gate voltage range, in our case, always corresponds to multiband (dxy and dxz,yz) occupation, as identified in the Hall effect (Supplementary Fig. S14). Then, the π channel can be linked to both intra-orbital spin-singlet states with superconducting order parameters with opposite sign9,18,19 or inter-orbital spin-triplet pairs8 and can be generally stable in the presence of inhomogeneous spatial conditions as well as inversion symmetry breaking. This implies that a time-reversal invariant superconductor with local intra-orbital singlet and triplet pairs is compatible with the occurrence of independent π and φ0 channels that are gate tunable.
We note that our data are qualitatively similar to the recently reported anomalous Josephson effect in proximity-induced s+− superconducting state in SnTe nanowires with ferroelectric domain walls51. In this work, however, the π-pairing leads to a time-reversal broken state that in turn would support a spontaneous zero-field critical current with asymmetric magnetic field dependence and pronounced minimum at zero field but different patterns upon sign reversal of magnetic field and critical current. In our case, the application of a three-channel model with time-reversal symmetry breaking shows a lower degree of matching of the main features of the experimental results for inversion of the magnetic field orientation (details in the Supplementary information) and lacks the symmetry for inversion of the critical current \({I}_{c}^{+}({B}_{\perp })=-{I}_{c}^{-}(-{B}_{\perp })\). Therefore, we conclude that the inversion symmetry breaking is indeed sufficient to account for the occurrence of individual supercurrent channels with different phase shifts in the 2D oxide interface. The gate tunability of the observed effects highlights the role of inter-orbital pairing for the LAO/STO system that is dominantly active in the regime of the occupation of the dxy and dxz,yz bands and would account for the possibility to control the relative strength of different pairing components52.
Our results provide evidence for the coexistence of multi-channel unconventional pairing in a non-centrosymmetric oxide 2D superconductor and thus might open new routes for tailoring topological superconducting phases through precise control of band occupation and phase offsets in the different supercurrent channels.
Methods
Sample preparation
The main data presented in the article concern 5uc-LaAlO3 films grown on TiO2-terminated STO substrates by ablating a single crystal LAO target using pulsed laser deposition (λ = 248 nm) with fluence energy 1.0 Jcm−2 and laser repetition rate 1 Hz. The substrate was heated to temperature 700 °C and the film was deposited in an oxygen partial pressure pO2 = 10−4 mbar. The epitaxial growth was monitored using in situ reflection high-energy electron diffraction (RHEED). The RHEED showed clear intensity oscillations confirming layer-by-layer growth. After the growth, the film was annealed at 500 °C in an oxygen pressure ~300 mbar to avoid any oxygen deficiency that could lead to extrinsic conduction in the film.
Device patterning
The uniform bridge devices were patterned by the following steps: (1) Ti/Au contacts (5 nm Ti and 100 nm Au) were fabricated by lift-off technique and dc magnetron sputtering. This method provides low-ohmic contact resistance to the LAO/STO interface33. (2) A thin layer (~60 nm) of negative resist (ma-N2401) spinned on the LAO surface. (3) The resist mask was patterned by e-beam lithography (JEOL JBX-9300FS). (4) The sample was then plasma irradiated by a low energy Ar+ ion beam in an Oxford IonFab 300 Plus system using an inductively coupled plasma Ar+ source and 3-cm beam aperture. The sample was irradiated for ≤2 min with beam energy of 150 eV and a current density of 0.03 mAcm−2, which results in an insulating interface in areas not covered by the e-beam resist. The irradiation process does neither result in the physical removal of the LAO film nor in oxygen vacancies in the STO layer1,2,3. We monitored the resistance of the interface during the irradiation, and the process was stopped when resistance increased up to ~20 MΩ to prevent overexposure of the interface. The quality of the nanopatterning was checked by measuring the temperature-dependent sheet resistance before and after patterning, which indicated no change in the behavior in the temperature dependence of resistance R(T). In one device presented in Fig. 1a with a bridge width 1 μm, we fabricated a weak link of width d ~ 35 nm by creating a small opening in positive resist (950k PMMA A2) using EBL34. In this case, the sample was irradiated by low energy Ar+ ion beam for a relatively shorter time (≤1 min) compared to the first lithography to make sure that the resistance of the weak link remains in the quasi-metallic regime.
Transport measurements
The I–V characteristics and other transport measurements are performed in a dilution refrigerator (Oxford Triton), which is equipped with a combination of mu-metal shields and a superconducting lead shield protecting the samples from the background DC magnetic field component, with a residual field of less than 100 nT. The external noise is suppressed by using twisted pairs of superconducting NbTi/Cu lines and combination with two stages of cryogenic filters. A Cu powder filter was installed at the base temperature stage of the refrigerator, together with low-pass RC filters with a cutoff frequency of 0.2 MHz at the 4 K stage. The noise is further filtered by using conventional EMI filters at room temperature. The out-of-plane magnetic field is applied by using a Helmholtz NbTi/Cu superconducting coil, whereas the in-plane magnetic field is applied using a cylindrical NbTi/Cu superconducting coil that is capable of a maximum magnetic field of 25 mT. Room temperature low noise filter amplifiers were used for conventional pseudo-four-probe measurements of the I–V characteristics.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code that supports the findings of this study is available from the corresponding author upon reasonable request.
References
Sigrist, M. & Ueda, K. Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 63, 239–311 (1991).
Nam, H. et al. Ultrathin two-dimensional superconductivity with strong spin-orbit coupling. PNAS 113, 10513 (2016).
Saito, Y., Nojima, T. & Iwasa, Y. Highly crystalline 2D superconductors. Nat. Rev. Mater. 2, 16094 (2016).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Sohn, E. et al. An unusual continuous paramagnetic-limited superconducting phase transition in 2D NbSe2. Nat. Mater. 17, 504–508 (2018).
Ohtomo, A. & Hwang, H. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007).
Fukaya, Y. et al. Inter-orbital topological superconductivity in spin-orbit coupled superconductors with inversion symmetry breaking. Phys. Rev. B 97, 174522 (2018).
Scheurer, M. S. & Schmalian, J. Topological superconductivity and unconventional pairing in oxide interfaces. Nat. Commun. 6, 6005 (2015).
Fernandes, R. M. et al. Two-band superconductivity in doped SrTiO3 films and interfaces. Phys. Rev. B 87, 014510 (2013).
Caviglia, A. D. et al. Electric field control of the LaAlO3/SrTiO3 interface ground state. Nature 456, 624–627 (2008).
Thierschmann, H. et al. Transport regimes of a split gate superconducting quantum point contact in the two-dimensional LaAlO3/SrTiO3 superfluid. Nat. Commun. 9, 2276 (2018).
Hurand, S. et al. Field-effect control of superconductivity and Rashba spin-orbit coupling in top-gated LaAlO3/SrTiO3 devices. Sci. Rep. 5, 12751 (2015).
Caviglia, A. D. et al. Tunable Rashba spin-orbit interaction at oxide interfaces. Phys. Rev. Lett. 104, 126803 (2010).
Ben Shalom, M. et al. Tuning spin-orbit coupling and superconductivity at the LaAlO3/SrTiO3 interface: a magnetotransport study. Phys. Rev. Lett. 104, 126802 (2010).
Joshua, A. et al. A universal critical density underlying the physics of electrons at the LaAlO3/SrTiO3 interface. Nat. Commun. 3, 1129 (2012).
Herranz, G. et al. Engineering two-dimensional superconductivity and Rashba spin-orbit coupling in LaAlO3/SrTiO3 quantum wells by selective orbital occupancy. Nat. Commun. 6, 6028 (2015).
Singh, G. et al. Gap suppression at a Lifshitz transition in a multi-condensate superconductor. Nat. Mater. 18, 948–954 (2019).
Trevisan, T. V. Unconventional multi-band superconductivity in bulk SrTiO3 and LaAlO3/SrTiO3 interfaces. Phys. Rev. Lett. 121, 127002 (2018).
Bal, V. V. et al. Gate-tunable superconducting weak link behavior in top-gated LaAlO3/SrTiO3. Appl. Phys. Lett. 106, 212601 (2015).
Stornaiuolo, D. et al. Signatures of unconventional superconductivity in the LaAlO3/SrTiO3 two-dimensional system. Phys. Rev. B 95, 140502(R) (2017).
Kalaboukhov, A. A. et al. Homogeneous superconductivity at the LaAlO3/SrTiO3 interface probed by nanoscale transport. Phys. Rev. B 96, 184525 (2017).
Kuerten, L. et al. In-gap states in superconducting LaAlO3/SrTiO3 interfaces observed by tunneling spectroscopy. Phys. Rev. B 96, 014513 (2017).
Kalisky, B. et al. Locally enhanced conductivity due to the tetragonal domain structure in LaAlO3/SrTiO3 heterointerfaces. Nat. Mater. 12, 1091–1095 (2013).
Goble, N. J. et al. Anisotropic electrical resistance in mesoscopic LaAlO3/SrTiO3 devices with individual domain walls. Sci. Rep. 7, 44361 (2017).
Bert, J. A. et al. Direct imaging of the coexistence of ferromagnetism and superconductivity at the LaAlO3/SrTiO3 interface. Nat. Phys. 7, 767–771 (2011).
Caprara, S. et al. Inhomogeneous multi carrier superconductivity at LaXO3/SrTiO3 (X = Al or Ti) oxide interfaces. Supercond. Sci. Technol. 28, 014002 (2015).
Singh, G. et al. Competition between electron pairing and phase coherence in superconducting interfaces. Nat. Commun. 9, 407 (2018).
Biscaras, J. et al. Multiple quantum criticality in a two-dimensional superconductor. Nat. Mater. 12, 542–548 (2013).
Hurand, S. et al. Josephson-like dynamics of the superconducting LaAlO3/SrTiO3 interface. Phys. Rev. B 99, 104515 (2019).
Manca, N. et al. Bimodal phase diagram of the superfluid density in LaAlO3/SrTiO3 revealed by an interfacial waveguide resonator. Phys. Rev. Lett. 122, 036801 (2019).
Andersen, L. et al. Generalized Anderson’s theorem for superconductors derived from topological insulators. Sci. Adv. 6, eaay6502 (2020).
Aurino, P. P. et al. Nano-patterning of the electron gas at the LaAlO3/SrTiO3 interface using low-energy ion beam irradiation. Appl. Phys. Lett. 102, 201610 (2013).
Singh, G. et al. Nanopatterning of weak links in superconducting oxide interfaces. Nanomaterials 11, 398 (2021).
Tinkham, M. et al. Hysteretic I–V curves of superconducting nanowires. Phys. Rev. B 68, 134515 (2003).
Ron, A., Maniv, E., Graf, D., Park, J.-H. & Dagan, Y. Anomalous magnetic ground state in an LaAlO3/SrTiO3 interface probed by transport through nanowires. Phys. Rev. Lett. 113, 216801 (2014).
Jaccarino, V. & Peter, M. Ultra-high field superconductivity. Phys. Rev. Lett. 9, 290 (1962).
Gardner, H. J. et al. Enhancement of superconductivity by a parallel magnetic field in two-dimensional superconductors. Nat. Phys. 7, 895–900 (2011).
Kharitonov, M. Y. & Feigelman, M. V. Enhancement of superconductivity in disordered films by parallel magnetic field. JETP Lett. 82, 421–425 (2001).
Rogachev, A. et al. Magnetic-field enhancement of superconductivity in ultranarrow wires. Phys. Rev. Lett. 97, 137001 (2006).
Wei, T.-C. et al. Enhancing superconductivity: magnetic impurities and their quenching by magnetic fields. EPL 75, 943–949 (2006).
Chen, Y., Snyder, S. D. & Goldman, A. M. Magnetic-field-induced superconducting state in Zn nanowires driven in the normal state by an electric current. Phys. Rev. Lett. 103, 127002 (2009).
Chen, Y. et al. Stabilization of superconductivity by magnetic field in out-of-equilibrium nanowires. Phys. Rev. B 83, 054505 (2011).
Murani, A. et al. Long- to short-junction crossover and field-reentrant critical current in Al/Ag-nanowires/Al Josephson junctions. Phys. Rev. B 102, 214506 (2020).
Courtois, H., Meschke, M., Peltonen, J. T. & Pekola, J. P. Origin of hysteresis in a proximity Josephson junction. Phys. Rev. Lett. 101, 067002 (2008).
Kemmler, M. et al. Magnetic interference patterns in 0 – π superconductor/insulator/ferromagnet/superconductor Josephson junctions: effects of asymmetry between 0 and π regions. Phys. Rev. B 81, 054522 (2010).
Szombati, D. B. et al. Josephson ϕ0-junction in nanowire quantum dots. Nat. Phys. 12, 568–572 (2016).
Strambini, E. et al. A Josephson phase battery. Nat. Nanotechnol. 15, 656–660 (2020).
Jun-Feng, L., Huan, Z. & Jun, W. Novel 0-π transitions in Josephson junctions between noncentrosymmetric superconductors. Chin. Phys. B. 25, 097403 (2016).
Rahnavard, Y., Manske, D. & Annunziata, G. Magnetic Josephson junctions with noncentrosymmetric superconductors. Phys. Rev. B 89, 214501 (2014).
Trimble, C. J. et al. Josephson detection of time reversal symmetry broken superconductivity in SnTe nanowires. npj Quantum Mater. 6, 61 (2021).
Jouan, A. et al. Origin of the dome-shaped superconducting phase diagram in SrTiO3-based interfaces. Preprint at https://arxiv.org/abs/2104.08220v1 (2021).
Acknowledgments
R.C. and C.G. would like to acknowledge a useful discussion with F. Romeo. This research was funded by ERA-NET QUANTERA European Union’s Horizon H2020 project “QUANTOX” under Grant Agreement No. 731473 and Swedish Research Council (VR) grant number 2016-05256. E.L. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 707404. M.C. acknowledges support by the project “Two-dimensional Oxides Platform for SPINorbitronics nanotechnology (TOPSPIN)” funded by the MIUR-PRIN Bando 2017 – grant 20177SL7HC. We also acknowledge support from the Swedish infrastructure for micro- and nanofabrication—MyFab.
Funding
Open access funding provided by Chalmers University of Technology.
Author information
Authors and Affiliations
Contributions
The project was designed and supervised by A.K. The growth of thin films was performed by E.L. and A.K. Nanofabrication of devices was done by G.S. The electrical measurements were carried out by G.S., A.K., and T.B. The results were interpreted and discussed by A.K. and G.S. with the guidance from T.C., F.L., A.D.C., and D.W. C.G., R.C., and M.C. provided the theoretical model and performed calculations of the magnetic field dependence of critical current. The manuscript has been written by G.S., A.K., and M.C. with contributions from all authors. All authors have read and agreed to the published version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Singh, G., Guarcello, C., Lesne, E. et al. Gate-tunable pairing channels in superconducting non-centrosymmetric oxides nanowires. npj Quantum Mater. 7, 2 (2022). https://doi.org/10.1038/s41535-021-00406-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-021-00406-6
This article is cited by
-
Stoichiometric control of electron mobility and 2D superconductivity at LaAlO3-SrTiO3 interfaces
Communications Physics (2024)
-
Anomalous Josephson coupling and high-harmonics in non-centrosymmetric superconductors with S-wave spin-triplet pairing
npj Quantum Materials (2022)