Abstract
We perform magnetic susceptibility and magnetic torque measurements on the organic κ-(BEDT-TTF)2Hg(SCN)2Br, which is recently suggested to host an exotic quantum dipole-liquid in its low-temperature insulating phase. Below the metal-insulator (MI) transition temperature, the magnetic susceptibility follows a Curie–Weiss law with a positive Curie–Weiss temperature, and a particular \(M\propto \sqrt{H}\) curve is observed. The emergent ferromagnetically interacting spins amount to about 1/6 of the full spin moment of localized charges. Taking account of the possible inhomogeneous quasi-charge-order that forms a dipole-liquid, we construct a model of antiferromagnetically interacting spin chains in two adjacent charge-ordered domains, which are coupled via fluctuating charges on a Mott-dimer at the boundary. We find that the charge fluctuations can draw a weak ferromagnetic moment out of the spin singlet domains.
Similar content being viewed by others
Introduction
Typical phase transitions in condensed matter accompany either universal critical singularities or the competitions between two different orderings. The former is easily converted to the latter when additional degrees of freedom become relevant. In reality, there often appear intermediate situations where the interplay of several degrees of freedom affects the nature of the growth of correlations and low-lying excitations. In such cases, the phase transitions at low temperatures can be easily masked, and the order parameters suffer intrinsic inhomogeneities. Historical examples are the dynamically disordered charge stripes in high-Tc superconducting cuprates1,2, and the orbital disorders that trigger the colossal magnetoresistance in manganites3. The complexity of dealing with multiple correlated degrees of freedom such as charge, spin, orbital, and lattice often makes it difficult to pin down their dominant mechanism.
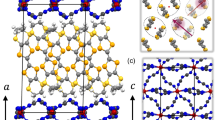
Organic κ-(BEDT-TTF)2X materials (Fig. 1a, b) become an ideal playground to study such an issue in a simpler setup. These materials form quarter-filled two-dimensional strongly correlated electronic systems, where molecular dimer (BEDT-TTF)2 connected by a large transfer integral td (see Fig. 1b) serves as a lattice site of a Mott insulator by hosting one charge per dimer. In these Mott insulators, the spin-1/2 interact antiferromagnetically as shown Fig. 1c and a quantum spin liquid phase is observed in κ-(BEDT-TTF)2Cu2(CN)3 (abbreviated as κ-CN) as well as a typical antiferromagnetism in κ-(BEDT-TTF)2Cu[N(CN)2]Cl (κ-Cu-Cl)4,5. If the degree of dimerization, namely the ratio of td to other inter-dimer transfer integrals (tB, tp, and tq), is weakened, the charges would no longer stay on the dimer-orbital, but rather localize to one side of the dimerized molecules to gain the intermolecular Coulomb interaction Vij, resulting in a charge-ordered phase. A charge degree of freedom enclosed in the dimer is interpreted as quantum electric dipole6,7, which is detected by anomalous frequency-dependence of dielectricity in many materials including κ-CN7, κ-Cu-Cl8, and EtMe3Sb[Pd(dmit)2]29,10. In that context, the dimer Mott and charge-ordered phases are interpreted as para and ferroelectricity6,11, separated by a typical Ising type second-order phase transition (see the phase diagram in Fig. 1d). However, when the universal criticality of dipoles couples to magnetism or lattice degrees of freedom, this transition can be masked and some inhomogeneous phases may emerge12. Indeed, the subtleties of the transition are recently disclosed by the fresh members of this family, κ-(BEDT-TTF)2Hg(SCN)2Br (κ-Hg-Br) and κ-(BEDT-TTF)2Hg(SCN)2Cl (κ-Hg-Cl), which have a relatively weak dimerization13 and fill the empty region of materials parameter space. In contrast to a simple Mott insulator, which shows a crossover from the high-temperature metallic regime4, these compounds show an abrupt increase of resistivity at the metal-insulator (MI) transition14. Raman spectroscopy reveals a distinct charge order in κ-Hg-Cl in the temperature range 15–30 K15 whereas κ-Hg-Br does not show any sign of regular charge ordering down to the lowest temperature16. The absence of magnetic order in κ-Hg-Br is also shown by the specific heat measurements down to 100 mK16. A picture of “quantum dipole liquid” is provided as an interpretation to the latter intriguing phase16, possibly consisting of dynamical charge-ordered domains enclosing electric dipole moments maximally amounting to 0.1e per dimer.
a Crystal structure of κ-Hg-Br viewed along the b-axis. The long molecular axis of BEDT-TTF is tilted by ~17∘ from the a-axis. b BEDT-TTF molecules in the b-c plane and the transfer integrals estimated as (td, tB, tp, tq) = (126, 83, 60, 40) meV (Valentí, R. & Jeschke, H. private communications and ref. 13). c Schematic illustration of the dimer Mott insulator and charge order. Charges on Mott-dimers (red circles) carry spin-1/2, and the exchange interactions between them \({J}_{{{{\rm{AF}}}}}\propto {t}_{{{{\rm{B}}}}}^{2}\) (vertical) and \({J}_{{{{\rm{AF}}}}}\propto {({t}_{{{{\rm{p}}}}}-{t}_{{{{\rm{q}}}}})}^{2}\) (diagonal directions) form an antiferromagnetic triangular lattice (red lines). In the charge-ordered state, the charges localized on one side of the dimer (green circles) form an antiferromagnetic quasi-one-dimensional spin-1/2 chain of \({J}_{{{{\rm{AF}}}}}\propto {t}_{{{{\rm{q}}}}}^{2}\) (green line). Inset: the Mott-dimer state is the linear combination of charge located on the left/right molecule, supported by large td. The charge order keeps the charge on one side of the dimerized pair to avoid the inter-site (inter-dimer) Coulomb interaction Vij = VB, Vp, Vq (indices follow those of tij). d Schematic phase diagram (Hotta, C., Yoshida, T. & Harada, K. unpublished) of the present system for low energy effective model of charges proposed in ref. 19, where (Vp − Vq) and VB account for the Coulomb interactions between charges on different dimers in diagonal and vertical directions, respectively. When Vij/2td ≳ 0.5–1, the charge order is realized. According to the first principles-based evaluation32, ((Vp − Vq)/2td, VB/2td) ~ (0.25, 0.48) for κ-Hg-Cl and (0.19, 0.42) for κ-Hg-Br.
We report the experimental evidence of intrinsic ferromagnetic exchange interactions emerging in the clean bulk crystal of κ-Hg-Br, indicated by a positive Curie–Weiss temperature of ΘCW = 16 K, where about 1/6 of the full spins of localized charges contribute. We find that the M–H curve at low temperature follows \(M\propto \sqrt{H}\), showing a very rapid onset with a small field. Although the square-root onset of the M–H curve is well-known for a gapped quasi-one-dimensional quantum magnet near the critical field17,18, it is qualitatively different from the present gapless \(M\propto \sqrt{H}\) that continues up to a large field. It does not resemble any of the M–H profile of the magnetism known so far, such as the H-linear antiferromagnetic magnetization or the paramagnetic Brillouin curve. Such robust ferromagnetic Curie–Weiss law just above the antiferromagnetic singlet ground state can be scarcely found in nature, except for those originating from magnetic impurities or a spin glass, both of which are excluded in the present case by the lack of remnant filed or hysteresis in magnetization. Since no existing theory on bulk magnetism both for the localized spins or itinerant electrons can be applied, we construct a synergetic quantum-spin model that includes the effect of charge fluctuation. The starting point is the low-temperature inhomogeneous state of charges that appear by masking the phase transition in Fig. 1d. We take account of the already existing idea of a short charge correlation length and the robustly remaining charge fluctuation at the simplest level16,19. The model represents spins on two charge-ordered domains which couple to dimer-spins carried by fluctuating charges at the domain boundary, and successfully shows how ferromagnetic behavior can originate from the charge fluctuation. The theory thus explains the properties disclosed by the magnetic susceptibility and torque measurements.
Results
Magnetization measurements
Figure 2a, b show the temperature dependence of the magnetic susceptibility χM(T)( = M/H) of κ-Hg-Br. The MI transition is observed at TMI ~90 K (the inset of Fig. 2a). Above this temperature, χM(T) shows a Pauli-paramagnetic behavior, while below TMI it starts to increase abruptly on lowering the temperature. A Curie–Weiss fit for 20–70 K (the solid line in Fig. 2b) gives a positive ΘCW ~16 K with the Curie constant C = 0.060 emu K mol−1. This positive ΘCW provides strong evidence of a ferromagnetic interaction between spins. The C value shows that ~1/6 of the total spins contribute to the Curie–Weiss paramagnetism with the ferromagnetic interaction. The 1/6-concentration is intrinsic to the ferromagnetic behavior, as χM(T) does not depend on the measured field strength below 5 T in this temperature range (see Supplementary Fig. 2 in Supplemental Information (SI)). Similar χM(T) was observed previously20. However, our data shows the ferromagnetic ΘCW more clearly in a wider temperature range (see Section A in SI for a comparison). To the best of our knowledge, this compound is the first to show such ferromagnetic behavior in a family of organic Mott insulators κ-(BEDT-TTF)2X and X[Pd(dmit)2]2. If one interprets this χ as the one from the ferromagnetic Heisenberg chain 21, the effective ferromagnetic coupling constant is evaluated as JF ~ ΘCW/Θ = 53 K, with Θ = 0.3036.
a Temperature dependence of the magnetic susceptibility (χM(T)) at 1 T. Data obtained by field cool (FC) and zero-field cool (ZFC) are shown by filled and open symbols, respectively. The inset shows an enlarged view of χM(T) near TMI = 90 K. b Temperature dependence of the inverse susceptibility. The solid line shows a linear fit for 20–70 K. c Field dependence of the magnetization M at 2.0 K, measured in the order of (1) 0 to 5 T, (2) +5 to −5 T, and (3) −5 to 0 T. The solid and the dashed lines show a fit to \(M\propto \sqrt{H}\) and the Brillouin function at 2.0 K, respectively. The inset shows the field dependence of M2 of the same data.
The particular ferromagnetic behavior is also found in the field dependence of the magnetization M. The linear M–H curve at high temperatures becomes nonlinear at 2.0 K as shown in Fig. 2c (see also Supplementary Fig. 2 in SI for the temperature dependence). Below 2 T, M increases faster than the Brillouin curve (the dashed line in Fig. 2c). Remarkably, we find that M exhibits a particular field dependence of \(M\propto \sqrt{H}\) as shown in the solid lines in Fig. 2c and the inset.
Magnetic torque measurements
This \(\sqrt{H}\) dependence of M is further confirmed to persist up to 17.5 T by our magnetic torque measurements done for one single crystal. Figure 3a shows the field dependence of the magnetic torque obtained from a fixed-angle high-field torque measurement at 0.12 and 1.7 K. As shown in Fig. 3a, the magnetic torque shows the field dependence of H3/2 (the dashed line in Fig. 3a). Given the form of the magnetic torque M × H, the field dependence of H3/2 shows \(M\propto \sqrt{H}\). Note that the free impurity spins are not responsible for this magnetization, since otherwise, the saturation should take place at ~1 T for 0.12 K, which is not observed in our data.
a Field dependence of the magnetic torque up to 17.5 T at 0.12 and 1.7 K. The amplitude of the 2θ component of the magnetic torque curve obtained by the rotating magnetic field in the a-c plane is plotted. The dashed line shows a fit of H3/2 field dependence, indicating \(M\propto \sqrt{H}\) up to 17.5 T. b Low-field data of the magnetic torque at 5, 10 and 20 K. The field angle was fixed at 45° from the c-axis to the a-axis. Field sweep is given as (1) \(0\to +{H}_{\max }\), (2) \(+{H}_{\max }\to -{H}_{\max }\), and (3) \(-{H}_{\max }\to 0\).
Throughout the whole sweep of H, the M–H curve shows neither a remnant field nor a hysteresis (Fig. 2c). The absence of hysteresis is further confirmed down to the lowest fields by our magnetic torque measurements (Fig. 3b). Our data excludes the spin-glass-based weak ferromagnetism picture presented in the previous study20, because both a ferromagnetic state22 and a spin glass state23 is known to exhibit clear hystereses in the torque measurements from a remnant field and a frozen moment, respectively. In ref. 20, the authors analyzed the magnetic susceptibility consistent with ours (see Section A in SI) using a narrower fitting range and concluded the antiferromagnetic Curie–Weiss temperature. They speculated that such behavior comes from the spin-glass and the ferromagnetic polarons that may emerge in the presence of charge carriers. However, the studied material has no such carriers, and our torque measurement excludes the spin-glass picture. Their picture on weak ferromagnetism is qualitatively different from ours.
To investigate the magnetic state below TMI in detail, we measured the magnetic torque curves by rotating the magnetic field in the a-c plane (Fig. 4a), where θ denotes the angle between the field and the a-axis (see Fig. 4d). The magnetic torque signal, \({\tau }_{{{{\rm{mag}}}}}={\tau }_{2\theta }\sin 2(\theta -{\phi }_{2\theta })\), is obtained after subtracting the \(\sin \theta\) component that comes from the gravity of the sample mass (see Section C in SI for details). These magnetic torque curve measurements allow us to detect the magnitude of the magnetic anisotropy, which is proportional to the amplitude of the 2θ component divided by H2 (Fig. 4b), and the direction of the magnetic principle axis by the phase ϕ2θ (Fig. 4c). In the metallic T > TMI phase, ϕ2θ stays at around −20°, which is close to the angle between the long axis of BEDT-TTF molecules and the a-axis (see Fig. 1a), showing that the magnetic anisotropy comes from the spins on the BEDT-TTF dimers24,25,26.
a Magnetic torque curves at different temperatures, normalized by H2 to compare the ones for different fields (see Section C in SI for details). The data below (above) 40 K was measured at 1 T (3 T). b, c Temperature dependence of the torque amplitude τ2θ divided by H2 (b) and the phase shift ϕ2θ (c) of \(\sin 2\theta\) component of the torque curve. The magnetic susceptibility shown in Fig. 2a is also plotted on the right axis as the dashed line in (b). d Schematic drawing of magnetic torque measurement by a resistive cantilever.
At TMI, ϕ2θ shows a sharp jump which is followed by a rapid shift of ϕ2θ toward zero, while at the same time τ2θ stays nearly temperature independent in contrast to the increase of χM(T). These contrasting temperature dependencies indicate that the magnetic principle axis varies concomitantly with the decrease of the magnetic anisotropy below TMI. Since Raman16 and IR14 measurements observed no change of the phonon spectrum below TMI, the change of ϕ2θ cannot be attributed to the rotation of the BEDT-TTF molecules. Therefore, this ϕ2θ shift is given by an emergence of a magnetic easy axis parallel to the a axis caused by the ferromagnetic interaction appearing below TMI. A similar but much smaller phase shift has been observed in κ-CN26, which may be ascribed to an additional moment from valence bond defects27. We further find a characteristic temperature T* ~24 K. Below T*, ϕ2θ drops, τ2θ/H2 increases, and both τ2θ/H2 and ϕ2θ starts to depend on the field strength. The increase of the magnetic anisotropy particularly developing below T* is consistent with the anisotropy of χM(T) observed in the previous measurement20, supporting the magnetic origin of these temperature changes. This temperature-dependent change is larger for lower fields; as we saw in Fig. 3b the torque data at ∣H∣ ≲ 0.5 T changes its sign below 20 K. Another bump-like feature in ϕ2θ is observed around 7 K, implying a further change of the magnetic state. These features might be related to the changes of the relaxation times observed in NMR measurements done at higher fields28. We thus observed a distinct change in the magnetic property already starting below TMI via two torque parameters. Further magnetic torque measurements performed in a dilution refrigerator reveal no change in the magnetic torque below 2 K (Fig. 3a), showing saturation of the temperature dependence.
Discussion
Our magnetic measurements on κ-Hg-Br disclose an unconventional magnetic state, which to our best knowledge has never been observed in the other family members of κ-(BEDT-TTF)2X – the ferromagnetic ΘCW, the non-hysteretic M–H curve with \(M\propto \sqrt{H}\) at low temperatures, and the large change in the direction of the magnetic principle axis.
Let us first start by elucidating the way the charges are localized at T < TMI. Most of the previously known κ-(BEDT-TTF)2X become a dimer Mott insulator depicted schematically in Fig. 1c. In a Mott phase, the dominant magnetic interactions between the spins carried by the localized charge are always antiferromagnetic as they originate from the kinetic exchange as, \({J}_{{{{\rm{AF}}}}}=4{t}_{ij}^{2}/(U-{V}_{ij})\) where tij and Vij are the transfer integrals and intermolecular Coulomb interaction along the exchange bond, and U is the on-molecular Coulomb interaction. Then, the antiferromagnetic order of κ-Cu-Cl and quantum spin liquid nature of κ-CN are roughly understood by the square-like and triangular lattice geometry of JAF which amounts to 50029 and 250 K30, respectively. These values of JAF are evaluated consistently from both the experiments as well as first-principles calculation where one may consider the actual Coulomb interaction to be 30–40% smaller than the ab initio based ones (see Section D in SI). Therefore, the positive ΘCW observed in κ-Hg-Br cannot be explained by the magnetism of a dimer Mott insulator.
In fact, the abrupt increase of resistivity just below TMI in both κ-Hg-Br and κ-Hg-Cl is different from the crossover behavior usually observed in dimer Mott materials4, signaling some sort of translational symmetry breaking of charge distribution. However, the Raman spectroscopy measurements indicate the absence of static charge ordering in κ-Hg-Br16. A scenario compatible with all these findings is the dynamical and inhomogeneous charge distribution in between the dimer Mott and charge-ordered state. The intra-dimer transfer integral from the first-principles calculation on κ-Hg-Br is td ~120 meV (Valentí, R. & Jeschke, H. private communications and ref. 13), much weaker than the typical value ~200 meV of the κ-salts31, and thus a quasi-charge-order by the inter-dimer Coulomb interactions is a reasonable expectation.
In Fig. 1d, we locate κ-Hg-Br and κ-Hg-Cl according to the first-principles-based evaluations32. In the uniform charge-ordered case possibly realized in κ-Hg-Cl, JAF forms long quasi-one-dimensional (1D) chains (see the green lines in Fig. 1c). Here the vertical stripe charge configuration is possibly favored for the Coulomb-interaction-strength of Vq < Vp, VB of the material32.
When the static and bulk charge order is no longer stabilized in κ-Hg-Br, these chains shall break up into short fragments separated by Mott-dimers, as shown in Fig. 5a. The way to construct the domain is not really random; we assume that the chain length N roughly corresponds to the correlation length of charges, and a Mott-dimer is inserted between the chains running in the tq direction, while in reality sometimes there will be connections with the dimers through tp in the other directions. Inside the 1D fragment, the spins interact along the tq-bonds via JAF ~170–300 K, which will give td/JAF ~4–8 (see Section D in SI). The charge on a Mott-dimer fluctuates, with fluctuation parameters defined by td values. During these fluctuations, the charge (and relevant spin) occupies either the left or right molecule on the dimer and interacts with S = 1/2 (green circle) at the adjacent left/right end of the chain via JAF. For the charge configuration shown in Fig. 5a, JAF shown in green and red bonds have the same amplitude.
a One possible charge configuration of κ-Hg-Br with a charge-ordered domain separated by the Mott dimer. The ordered charges (green circle) carry spin-1/2 and form an antiferromagnetic spin chain along with the green bond. The charge on Mott dimer fluctuates via td between dimerized two molecules, and when it occupies one side of the dimerized molecule which finds a green-colored charge on the nearest neighbor site connected by either of tB, tp, or tq (see Fig. 1b), it interacts via JAF colored with red bond. b Illustration of the model described by Eq. 1. Arrow represents the dimer-spin. c Correlation 〈SL ⋅ SR〉 between spins on the left and right chain for several series of N = NL + NR + 1, for the two lowest energy states, with dominant ferromagnetism 〈SL ⋅ SR〉 > 0 (see Section E in SI). Red (blue) symbols indicate the data of the first-excited (lowest) states. d Magnetization density at site-i of the first excited state of Eq. 1 with NL = NR = 10 and Sz = 3/2. It consists of the equal weight superposition of upper and lower panels with dimer-spin (in the gray region) on the right and left. e Magnetization density of the first excited state of Eq. 1 as a function of excitation energy ΔE per spin for NL, NR = 8–100, where the absolute values of the curve may shift within the shaded region when we change the ratio of left and right chains down to NR ~ NL/2. All give the magnetization curve in a square-root(broken line) form by interpreting the horizontal axis as a magnetic field. The gray and blue bold lines (solid part:SQUID, broken part:torque) are the experimental results with the vertical axis in a unit of μB/2, when scaling the horizontal axis as JAF/kB ~170 and 300 K as a unit of ΔE, respectively.
To elucidate how these quantum fluctuations modify the dominant antiferromagnetism, we construct a synergetic model consisting of two open chains with NL and NR spin-1/2’s and a single electron with S = 1/2 (which we call dimer-spin) as shown in Fig. 5d. The Hamiltonian is given as
where Siγ is the spin on site-i on left and right chain (γ = L/R), \({c}_{{{{\rm{L/R}}}}}^{{\dagger} }\) and cL/R are the creation and annihilation operator of charges on the left/right molecule of the dimer with its number operator \({n}_{{{{\rm{L/R}}}}}={c}_{{{{\rm{L/R}}}}}^{{\dagger} }{c}_{{{{\rm{L/R}}}}}\), and Sd is the dimer spin. This model cuts out the locally interacting manifold of spins shown in Fig. 5a. Such charge configurations behind the model are expected for κ-Hg-Br at temperatures less than TMI, where we find no indications of long-range order of both charges and spins. Experimentally, the charges in an ordered domain show intra-dimer fluctuation altogether via 1.3 THz 15. In Eq. 1 we have JAF/kB ~170 K of the same energy scale, which however originates from the inter-dimer charge fluctuation of tq ~465 K, larger by an order of magnitude. The former is regarded as nearly “static” and are not explicitly seen in our model. The dimers having the td-term fluctuate alone and do not contribute to the fluctuations of the chains with 1.3 THz frequency. The details of an electronic state below T* are not really known, but the present model does not contradict with the experimental reports given so far.
The model is solved numerically by combining the exact diagonalization calculations (see Section D in SI). Since the total-Sz of Eq. 1 is a conserved quantity, we analyze the model by dividing the Hilbert space into different Sz-sectors and evaluating the lowest energy levels for each sector. Figure 5c shows 〈SL ⋅ SR〉 between spins on the left and right chains, Sγ = ∑j∈γSj for several different series of Nγ and system length N. One finds a dominant ferromagnetic correlation (〈SL ⋅ SR〉 > 0) for large portions of the two lowest excited states. Representative spatial distribution of spin moments for a slightly polarized state is shown in Fig. 5d; the contribution from the constituents of the wave function with dimer-spin on the right and left are separately drawn. The left-upper panel is a typical spin distribution with twofold periodic Friedel oscillation generated by the two open edges of the chain33. The dimer-spin hops back and forth, and mixes quantum mechanically with the spins on closer edges of the chains and suppresses their moments. The moments are redistributed throughout the chains and are accumulated densely on the further edges from the center. They point in the same orientation mediated by fluctuating spins closer to the dimer-spin (top panel of Fig. 5d). This interplay of td and JAF generates robust quantum ferromagnetism (Fig. 5e), which is insensitive to the value of td and the choice of Nγ (see Section E in SI for details).
The theory explains the square-root behavior of the M–H curve at low temperature in κ-Hg-Br. Our calculations show that the ground state of Eq. 1 with even N is always nonmagnetic and has a dominant antiferromagnetic correlation. Let us consider exciting a magnetic moment by applying a magnetic field. Suppose that for an isolated chain with fixed NL and NR, the lowest eigenenergy of Eq. 1 for each Sz sector is given as E(Sz). In an applied field H, the system acquires a finite magnetization Sz that gives the minimum of energy \({E}_{H}={\min }_{{S}_{z}}\left(\right.E({S}_{z})-{S}_{z}H\left)\right.\). The “magnetization curve” at finite NL, NR is given as such that H(Sz) = ΔE/ΔSz, where ΔE is the energy difference E(Sz) − E(Sz − 1) for ΔSz = 1. As mentioned earlier, the magnetism of the short-range charge-ordered phase shall be described by the assemblage of small magnetic subsystems, interacting with each other, connected with more than two neighboring subsystems. Since the information on the distribution of the chain length is missing, and since the calculation is dealing with only two interacting segments, the direct comparison of the theory and experiments may seem difficult. However, we find that an unbiased comparison is possible as shown in Fig. 5e, where we plotted the magnetization density Sz/N as a function of ΔE/N of the subsystems with various different NL and NR. Here, since all the data form a universal square-root curve regardless of the chain length N, it can be interpreted as a stochastic magnetization curve against magnetic field H/JAF. As found in the logarithmic plot, the functional form, \({{\Delta }}E/N \sim C\sqrt{{S}_{z}/N}\), always holds regardless of the length of the chains, while the constant C may depend on the ratio of NL and NR. The universal square-root behavior insensitive to N means that the energy is determined locally. Accordingly, if we consider a bulk assemblage of segments of chains connected by Mott-dimers, their energy shall be an extensive quantity, i.e., the summation of local energy gains. Therefore, we consider this functional form to be intrinsic.
The experimental data is plotted together in Fig. 5e where we add the magnetic torque data (data in Fig. 3a divided by H) into the field dependence of the magnetization data by SQUID (the data in Fig. 2c as it is) so that M estimated from τ2θ/H coincides to M of the SQUID data at 5 T. The horizontal axis of the experimental data is determined by the value of JAF, and is illustrated for the two parameter choices of JAF/kB = 170 and 300 K discussed in Section D in SI. The shaded region represents the vertical range over which the absolute value of the magnetic moment may vary if the distribution of chain lengths has a large variance, and hence one may state that the theory shows good qualitative agreement with the experiment for any comparable choice of JAF.
An extrapolation of the experimental data in Fig. 5e shows that the magnetization reaches μB/6 at about 20–30 T. Therefore, approximately, the field strength of 20–30 T which is comparable to T* = 24 K, gives the energy scale to excite the 1/6 magnetic moment from the nonmagnetic ground state. At the temperature range T* < T < TMI, such 1/6 moment is thermally excited and contributes to the ferromagnetism; the ferromagnetically coherent orientation of the moment would contribute to the phase shift of ϕ2θ. There, M–H curve no longer has a square root, because the low energy magnetic excitations are smeared out. The energy scale of μBH ~ 0.1JAF to have the μB/6 moment is consistent with 20–30 T.
Also, the preserved SU(2) symmetry in Eq. 1 matches with the restored isotropy in the magnetic torque at T < TMI. Notice that this ferromagnetic phase is not a long-range order but a correlation because of the one-dimensionality, as can also be suggested from the lack of hysteresis. Below T* the nonmagnetic ground state component becomes dominant. From Raman spectroscopy measurements, the static charge ordering is excluded, whereas the broad peak in ν2 mode is still compatible with quasi-charge-ordered domains with a variant charge disproportionation maximally amounting to ±0.1e, which are coherently fluctuating together inside the domain with a frequency estimated as 1.3 THz14,16.
Once the temperature falls below T*, the dipole (charge) degrees of freedom become correlated over a length scale ξ whose T-dependence saturates and fluctuates slowly together at a corresponding timescale. These fluctuations can safely be integrated out (see ref. 6), leading to the effective model of Eq. 1 for spins with antiferromagnetic interactions on chain segments of average length ξ.
While evaluating the precise character of the charge distribution is beyond the scope of any theory currently available, in Section F in SI we provide a phenomenological treatment performed by assuming a functional form for ξ(T) that is valid throughout the critical regime. Within this approach, we show that χ manifests a Curie–Weiss-like behavior that reflects the ferromagnetic correlations between thermally excited spins at temperatures T > T*. Further experimental information concerning the functional form of ξ(T) is required to verify this type of treatment.
One may suspect that the spin models with extrinsic impurities can also explain the phenomena. Although the possibility of spin glass is experimentally excluded, its quantum analog, the random singlet phase may share a similar feature with the present magnetism34; most of the spin moments form a singlet and the remaining spins may contribute to the magnetism. However, for such a state to happen one needs a large amount of static randomness in the distribution of JAF = J(1 ± Δ) that amounts to Δ ≳ 0.634, which cannot happen in the present system.
Ferromagnetism is elusive; For molecular-based materials with only light elements, few ferromagnetic compounds are known, e.g., p-NPNN35, C60(TDAE)0.8636, and (Et-4BrT)-[Ni(dmit)2]237, whose exchange interactions originate from the higher-order Goodenough–Kanamori rule. Other mechanisms of bulk ferromagnetism known so far are the Nagaoka ferromagnetism38, flat-band39, and double exchange or multi-orbitals Hubbard models40,41,42, which are applied to metals. The present finding should thus be the first proposal of generating a robust ferromagnetic exchange from the inhomogeneous charge distribution forming dominant spin singlet (paramagnet) by the leading antiferromagnetism interactions.
Naively, our ferromagnetism can be viewed as a local double-exchange; a single charge hops back and forth inside the dimer, and since it interacts with the spin chains on both sides, it is favorable to have both points in the same direction to maximally gain the antiferromagnetic exchange interaction. The difference from the double exchange is that the kinetics of charge is local, keeping the insulating character, and the weakly coupled one-dimensional fragments of spin chains do not allow the development of coherent ferromagnetic long-range order.
By designing a three-dimensional critical phase in between the charge order and dimer Mott insulator a two-dimensional ferromagnet might be available, in which case the ferromagnetic long-range order is allowed at a finite temperature.
Methods
Synthesis
Single crystals of κ-(BEDT-TTF)2Hg(SCN)2Br were grown by electrochemical oxidation of the BEDT-TTF solution16. In this synthesis, many single crystals with a variety of the size were obtained. We used a batch of the smaller crystals (powder samples, 3.73 mg) for the SQUID measurements and picked up larger ones for the magnetic torque measurements.
Measurement setups
The magnetic susceptibility of powder samples was measured by SQUID for 2.0–300 K. The magnetic torque measurements were carried out for one single crystal with dimensions 0.75 mm3 × 0.57 mm3 × 0.13 mm3 attached to a piezo-resistive cantilever by a tiny amount of grease (see Supplementary Fig. 3a in SI) by using a variable temperature insert (1.6–200 K) and a dilution refrigerator (0.09–2.5 K). The magnetic torque (τmag = M × H) is measured by the change of the resistance of the piezo-resistive cantilever. The temperature dependence of the sensitivity of the piezo-resistive cantilever is calibrated by the \(\sin \theta\) component in the torque curve by the gravity of the sample mass as described in Section C in SI. The standard deviations of all the data shown in the figures are smaller than the symbol size.
Data availability
All the data that support the findings of this study are available from the corresponding authors (M.Y. and N.D.) upon reasonable request.
Code availability
All the numerical codes that support the findings of this study are available from the corresponding author (C.H.) upon reasonable request.
References
Kivelson, S. A., Fradkin, E. & Emery, V. J. Electronic liquid-crystal phases of a doped Mott insulator. Nature 393, 550–553 (1998).
Kivelson, S. A. et al. How to detect fluctuating stripes in the high-temperature superconductors. Rev. Mod. Phys. 75, 1201–1241 (2003).
Salamon, M. B. & Jaime, M. The physics of manganites: structure and transport. Rev. Mod. Phys. 73, 583–628 (2001).
Kanoda, K. Metal-insulator transition in κ − (ET)2X and (DCNQI)2M: two contrasting manifestation of electron correlation. J. Phys. Soc. Jpn. 75, 051007 (2006).
Kanoda, K. & Kato, R. Mott physics in organic conductors with triangular lattices. Annu. Rev. Condens. Matter Phys. 2, 167–188 (2011).
Hotta, C. Quantum electric dipoles in spin-liquid dimer Mott insulator κ-ET2Cu2(CN)3. Phys. Rev. B 82, 241104 (2010).
Abdel-Jawad, M. et al. Anomalous dielectric response in the dimer Mott insulator κ − (BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 82, 125119 (2010).
Lunkenheimer, P. et al. Multiferroicity in an organic charge-transfer salt that is suggestive of electric-dipole-driven magnetism. Nat. Mater. 11, 755–758 (2012).
Abdel-Jawad, M., Tajima, N., Kato, R. & Terasaki, I. Disordered conduction in single-crystalline dimer Mott compounds. Phys. Rev. B 88, 075139 (2013).
Lazić, P. et al. Importance of van der Waals interactions and cation-anion coupling in an organic quantum spin liquid. Phys. Rev. B 97, 245134 (2018).
Naka, M. & Ishihara, S. Electronic ferroelectricity in a dimer Mott insulator. J. Phys. Soc. Jpn. 79, 063707 (2010).
Itou, T. et al. Slow dynamics of electrons at a metal–Mott insulator boundary in an organic system with disorder. Sci. Adv. 3, e1601594 (2017).
Gati, E. et al. Evidence for electronically driven ferroelectricity in a strongly correlated dimerized BEDT-TTF molecular conductor. Phys. Rev. Lett. 120, 247601 (2018).
Ivek, T. et al. Metal-insulator transition in the dimerized organic conductor \(\kappa -{({{{\rm{BEDT}}}}-{{{\rm{TTF}}}})}_{2}{{{\rm{Hg}}}}{({{{\rm{SCN}}}})}_{2}{{{\rm{Br}}}}\). Phys. Rev. B 96, 085116 (2017).
Hassan, N. M. et al. Melting of charge order in the low-temperature state of an electronic ferroelectric-like system. npj Quantum Mater. 5, 15 (2020).
Hassan, N. et al. Evidence for a quantum dipole liquid state in an organic quasi–two-dimensional material. Science 360, 1101–1104 (2018).
Affleck, I. Bose condensation in quasi-one-dimensional antiferromagnets in strong fields. Phys. Rev. B 43, 3215–3222 (1991).
Chitra, R. & Giamarchi, T. Critical properties of gapped spin-chains and ladders in a magnetic field. Phys. Rev. B 55, 5816–5826 (1997).
Hotta, C. Theories on frustrated electrons in two-dimensional organic solids. Crystals 2, 1155–1200 (2012).
Hemmida, M. et al. Weak ferromagnetism and glassy state in \(\kappa -{({{{\rm{BEDT}}}}-{{{\rm{TTF}}}})}_{2}{{{{\rm{Hg}}}}({{{\rm{SCN}}}})}_{2}{{{\rm{Br}}}}\). Phys. Rev. B 98, 241202 (2018).
Souletie, J., Rabu, P. & Drillon, M. Ferromagnetic Heisenberg chains: a description of the magnetic susceptibility from a noncritical scaling approach. Phys. Rev. B 72, 214427 (2005).
Pinterić, M. et al. Magnetic anisotropy and low-frequency dielectric response of weak ferromagnetic phase in κ − (BEDT-TTF)2Cu[N(CN)2]Cl, where BEDT-TTF is bis(ethylenedithio)tetrathiafulvalene. Eur. Phys. J. B 11, 217–225 (1999).
Fert, A. & Hippert, F. Anisotropy of spin-glasses from torque measurements. Phys. Rev. Lett. 49, 1508–1511 (1982).
Watanabe, D. et al. Novel pauli-paramagnetic quantum phase in a Mott insulator. Nat. Commun. 3, 1090 (2012).
Isono, T. et al. Gapless quantum spin liquid in an organic spin-1/2 triangular-lattice κ-H3(Cat-EDT-TTF)2. Phys. Rev. Lett. 112, 177201 (2014).
Isono, T., Terashima, T., Miyagawa, K., Kanoda, K. & Uji, S. Quantum criticality in an organic spin-liquid insulator κ-(BEDT-TTF)2Cu2(CN)3. Nat. Commun. 7, 13494 (2016).
Riedl, K., Valentí, R. & Winter, S. M. Critical spin liquid versus valence-bond glass in a triangular-lattice organic antiferromagnet. Nat. Commun. 10, 2561 (2019).
Le, T. et al. Disorder and slowing magnetic dynamics in \(\kappa {{\mbox{}}}-{{\mbox{}}}{({{{\rm{BEDT}}}}{{\mbox{}}}-{{\mbox{}}}{{{\rm{TTF}}}})}_{2}{{{\rm{Hg}}}}{({{{\rm{SCN}}}})}_{2}{{{\rm{Br}}}}\). Phys. Rev. B 102, 184417 (2020).
Smith, D. F. et al. Dzialoshinskii-Moriya interaction in the organic superconductor \(\kappa -{({{{\rm{BEDT}}}}-{{{\rm{TTF}}}})}_{2}{{{\rm{Cu}}}}[{{{\rm{N}}}}{({{{\rm{CN}}}})}_{2}]{{{\rm{Cl}}}}\) . Phys. Rev. B 68, 024512 (2003).
Shimizu, Y., Miyagawa, K., Kanoda, K., Maesato, M. & Saito, G. Spin liquid state in an organic Mott insulator with a triangular lattice. Phys. Rev. Lett. 91, 107001 (2003).
Koretsune, T. & Hotta, C. Evaluating model parameters of the κ- and \({\beta }^{\prime}\)-type Mott insulating organic solids. Phys. Rev. B 89, 045102 (2014).
Jacko, A. C., Kenny, E. P. & Powell, B. J. Interplay of dipoles and spins in \(\kappa {{\mbox{}}}-{{\mbox{}}}{({{{\rm{BEDT}}}}{{\mbox{}}}-{{\mbox{}}}{{{\rm{TTF}}}})}_{2}{{{{X}}}}\), where \(X={{{\rm{Hg}}}}{({{{\rm{SCN}}}})}_{2}{{{\rm{Cl}}}},{{{\rm{Hg}}}}{({{{\rm{SCN}}}})}_{2}{{{\rm{Br}}}},{{{\rm{Cu}}}}[{{{\rm{N}}}}{({{{\rm{CN}}}})}_{2}]{{{\rm{Cl}}}},{{{\rm{Cu}}}}[{{{\rm{N}}}}{({{{\rm{CN}}}})}_{2}]{{{\rm{Br}}}}\), and \({\mathrm{Ag}_{2}({\mathrm{CN}})_{3}}\). Phys. Rev. B 101, 125110 (2020).
Shibata, N. & Hotta, C. Boundary effects in the density-matrix renormalization group calculation. Phys. Rev. B 84, 115116 (2011).
Shimokawa, T., Watanabe, K. & Kawamura, H. Static and dynamical spin correlations of the \(s=\frac{1}{2}\) random-bond antiferromagnetic Heisenberg model on the triangular and kagome lattices. Phys. Rev. B 92, 134407 (2015).
Takahashi, M. et al. Discovery of a quasi-1D organic ferromagnet, p-NPNN. Phys. Rev. Lett. 67, 746–748 (1991).
Allemand, P.-M. et al. Organic molecular soft ferromagnetism in a fullerene C60. Science 253, 301–302 (1991).
Kusamoto, T. et al. Bilayer Mott system with cation ⋯ anion supramolecular interactions based on a Nickel dithiolene anion radical: coexistence of ferro- and antiferromagnetic anion layers and large negative magnetoresistance. Inorg. Chem. 52, 4759–4761 (2013).
Nagaoka, Y. Ferromagnetism in a narrow, almost half-filled s band. Phys. Rev. 147, 392–405 (1966).
Tasaki, H. From Nagaoka’s ferromagnetism to flat-band ferromagnetism and beyond: an introduction to ferromagnetism in the Hubbard model. Prog. Theor. Phys. 99, 489–548 (1998).
Zener, C. Interaction between the d-shells in the transition metals. II. ferromagnetic compounds of manganese with perovskite structure. Phys. Rev. 82, 403–405 (1951).
Kubo, K. & Ohata, N. A quantum theory of double exchange. I. J. Phys. Soc. Jpn. 33, 21–32 (1972).
Sakamoto, H., Momoi, T. & Kubo, K. Ferromagnetism in the one-dimensional Hubbard model with orbital degeneracy: from low to high electron density. Phys. Rev. B 65, 224403 (2002).
Acknowledgements
The authors thank M. Urai for fruitful discussions. The work in JHU was supported as part of the Institute for Quantum Matter, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0019331. The work in Chernogolovka was carried out within the state assignment (number AAAA-A19-119092390079-8). The work in Japan was supported by KAKENHI (Grants-in-Aid for Scientific Research) Grants Nos. JP17K05533, JP18H01173, JP17K05497, JP17H02916, JP18H05225, JP18H05516, JP19K05397, JP19H01848, JP19K21842, JP21K03440, JP21K18597, and JP21H05191.
Author information
Authors and Affiliations
Contributions
M.Y., H.M. and N.D. conceived the project. E.I.Z., S.A.T. and R.N.L. prepared the single crystals. A.U., S.D., Y.S. and H.M. performed the magnetic susceptibility measurements. M.Y., S.S., T.T., S.U. and N.D. performed the magnetic torque measurements. C.H. is responsible for the whole theoretical part. M.Y., N.D. and C.H. wrote the manuscript. All the authors discussed the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yamashita, M., Sugiura, S., Ueda, A. et al. Ferromagnetism out of charge fluctuation of strongly correlated electrons in κ-(BEDT-TTF)2Hg(SCN)2Br. npj Quantum Mater. 6, 87 (2021). https://doi.org/10.1038/s41535-021-00387-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-021-00387-6