Abstract
Recently, the observation of large thermal Hall conductivities in correlated insulators with no apparent broken symmetry has generated immense interest and debates on the underlying ground states. Here, considering frustrated magnets with bond-dependent interactions, which are realized in the so-called Kitaev materials, we theoretically demonstrate that a large thermal Hall conductivity can originate from a classical ground state without any magnetic order. We discover a liquid state of magnetic vortices, which are inhomogeneous spin textures embedded in the background of polarized spins, under out-of-plane magnetic fields. In the classical regime, different configurations of vortices form an effectively degenerate manifold. We study the static and dynamical properties of the magnetic vortex liquid state at zero and finite temperatures. In particular, we show that the spin excitation spectrum resembles a continuum of nearly flat Chern bands, which ultimately leads to a large thermal Hall conductivity. Possible connections to experiments are discussed.
Similar content being viewed by others
Introduction
Thermal Hall conductivity in correlated insulators is an important diagnostic tool to uncover the underlying many-body ground states and bridging theories to materials. Recent observations of the half-quantized thermal Hall conductivity in the spin liquid candidate α-RuCl31,2, and a large thermal Hall signal in cuprates3, are just two prominent examples. As the charge transport is absent in these systems, collective degrees of freedom such as magnons and phonons, or charge-neutral fractionalized excitations in quantum spin liquids, are most likely to be the sources of such effects4,5,6,7. In this work, we present a novel route to obtain a large thermal Hall conductivity in frustrated magnets with nearest neighbor bond-dependent spin interactions4. Such interactions are realized in the so-called Kitaev materials8,9,10,11, which includes α-RuCl312,13 and Na2IrO314,15,16. In particular, we investigate the KΓ model on the honeycomb lattice with an external magnetic field along the [111] direction, where K > 0 is the antiferromagnetic Kitaev interaction17,18,19 and Γ < 0 is the symmetric anisotropic interaction. As discussed below, a more realistic generalization of this model is also studied. We consider the classical limit of these models, which enables numerical simulations on large systems.
At zero temperature, we discover an effectively degenerate ground state manifold of distinct spin configurations of magnetic vortices20 in an appreciable window of magnetic fields, right below the fully polarized state. In each configuration, the vortices are embedded in the background of polarized spins, and they do not form a crystalline order. The vortices decrease in number as the field increases, and eventually disappear completely as the system enters the fully polarized state. We call this manifold of states the classical magnetic vortex liquid in analogy to classical spin liquids21,22, as it is hugely degenerate at zero temperature and forms a thermal ensemble at finite temperatures like the latter. Instead of having disordered spins over the entire lattice with zero net magnetization as in classical spin liquids, the classical magnetic vortex liquid has disordered (i.e., randomly positioned) magnetic vortices in the background of polarized spins. While spin liquids evade magnetic orders, the vortex liquid avoids the crystallization of vortices.
The magnons from the background polarized state see the vortices as a source of fictitious magnetic field via the Berry phase effect23,24,25,26,27,28,29,30. In order to understand the spin excitation spectrum and quantify the thermal Hall response, we first use a mean-field approximation, where the magnetic flux carried by the vortices is spread over the entire system. In other words, the magnons see an averaged, uniform magnetic flux. The resulting magnon dispersion consists of many relatively flat bands and reveals a dense spin excitation spectrum at low energies, which looks very much like a continuum. It is found that the magnon bands are topologically nontrivial—they carry finite Chern numbers, which contribute constructively to a large thermal Hall conductivity31,32,33,34,35,36,37,38,39.
At finite temperatures, we employ Monte Carlo simulations and the Landau–Lifshitz equations of motion to investigate the static and dynamical properties of the classical magnetic vortex liquid. The vortex liquid is found to persist at finite temperatures, and it is separated by a crossover, rather than a sharp transition, from the high-temperature paramagnetic state. The equal-time spin correlator indeed reveals the characteristics of a liquid state. On the other hand, the dynamical structure factor exhibits a continuum of spin excitations, which strongly resembles the excitation spectrum obtained in the mean-field approximation.
Furthermore, we investigate the relevance of the classical magnetic vortex liquid to α-RuCl3 and similar materials. Reference 40 identifies a self-dual transformation of the \(JK{{\Gamma }}{{\Gamma }}^{\prime}\) model, where J is the Heisenberg interaction and \({{\Gamma }}^{\prime}\) is another off diagonal interaction. Under this transformation, the \(JK{{\Gamma }}{{\Gamma }}^{\prime}\) model is mapped to the same model yet with a different set of parameters \(\tilde{J}\), \(\tilde{K}\), \(\tilde{{{\Gamma }}}\), and \(\tilde{{{\Gamma }}}^{\prime}\). We verify that in the dual model of the KΓ model with K > 0 and Γ < 0, the sign of \(\tilde{K}\) is always negative (i.e., ferromagnetic), while that of \(\tilde{{{\Gamma }}}\) is positive for ∣Γ/K∣ < 4/5. Such a sign structure is the same as that in α-RuCl341,42,43,44,45. The resulting ground states of the dual models in a [111] magnetic field are in one-to-one correspondence. More interestingly, if we continuously evolve the dual model towards the parametric regime relevant to α-RuCl3, we find a significant extent of the vortex liquid at high fields, while the ground state at zero and low fields becomes the zigzag magnetic order13,46.
Results
Model
We start with the classical KΓ model on the honeycomb lattice, with K > 0 and Γ < 0, under an external magnetic field h along the [111] direction (perpendicular to the lattice plane),
where (λ, μ, ν) is a cyclic permutation of (x, y, z), K is the Kitaev interaction, Γ is the symmetric anisotropic interaction, and the field \({\bf{h}}=h(1,1,1)/\sqrt{3}\). The spins Si are treated as three-component vectors of fixed magnitude, ∣Si∣ = S. We can specify S = 1/2 for example, but we will keep the factor S explicit when discussing quantities such as field, energy, and temperature later. We adopt the trigonometric parametrization of the interactions, \(K=\cos \varphi ,{{\Gamma }}=-\sin \varphi\), with φ ∈ [0, π/2].
Emergence of classical magnetic vortex liquid
We use classical simulated annealing to obtain the zero temperature spin configuration on a lattice of L × L unit cells (or L × L × 2 sites), up to L = 36. The ground state phase diagram is explored as a function of φ and h. Periodic boundary conditions are imposed to reduce finite-size effect. We refer interested readers to refs. 47 and 48 for details of the simulated annealing calculation.
We observe a rather unusual phase at high fields right below the polarized state, which has a wide extent in φ. This phase is characterized by magnetic vortices, each consisting of a cluster of spins, forming an irregular, fluid-like pattern as opposed to a crystalline order, in the background of polarized spins. See Fig. 1 for example. The random distribution of magnetic vortices leads to many different spin configurations with similar energies, which effectively form a degenerate manifold. We call each spin configuration a random vortex configuration, and the degenerate manifold the classical magnetic vortex liquid. The density of vortices in the lattice depends on the magnitude of the field. At high fields near the polarized regime, the vortices are dilute, i.e., well separated from each other (e.g., see Supplementary Fig. 1a). As the field is lowered, the vortices become dense enough such that their boundaries overlap (e.g., see Supplementary Fig. 1b). The phase transition from the vortex liquid to the polarized state is a most likely a crossover. As the field increases, the density of vortices decreases continuously to zero, and the system gradually becomes polarized.
A random vortex configuration obtained via classical simulated annealing, at φ/π = 0.2 and h/S = 1.12, on a lattice of 30 × 30 × 2 sites with periodic boundary conditions. The [111] direction points out of plane, along which most spins are polarized. Color of the spins indicates the magnitude of the (normalized) transverse magnetization S⊥/S. Classical magnetic vortex liquid is a degenerate manifold of many random vortex configurations like this. More random vortex configurations can be found in Supplementary Figs. 1–3.
Figure 2 is a schematic phase diagram which indicates the range of parameters where the vortex liquid, labeled as “VL”, appears. Certainly, there exist other phases in the parametric region below the vortex liquid. Among them is a dominant 18-site order (i.e., a magnetic order with 18 sublattices per unit cell), a vortex crystal (i.e., vortices forming a crystalline order), and possibly some incommensurate order. However, these phases are not our main concern in this work, so we label them collectively as “18-site and others”. The nature of the lower phase transition of the vortex liquid depends on the low-field phase preferred by the interaction parameters. If the transition is into the vortex crystal, then it is discontinuous, as the vortex crystal has a different symmetry than that of the vortex liquid, which is analogous to the phase transition between solid and liquid. However, the transition may be into some incommensurate order, whose nature is obscured by finite-size effect.
Some additional remarks on the vortex liquid are given in Supplementary Note 1. Here, we explain why the vortex liquid is very likely the ground state in the relevant parametric regime, based on the results of our numerical investigation. Generally speaking, although simulated annealing is in essence a variational approach that does not always guarantee the true ground state, it should yield a state that well approximates the true ground state. Also, as in any numerical simulation of a physical system, we have to work with finite system sizes. However, when (i) the system size is much larger than the size of a single vortex and the number of vortices is small, and (ii) the system size is commensurate with the vortex size as to allow for a vortex crystal, we consistently obtain the random vortex configurations from multiple simulated annealing trials. We can also compare the averaged energy of the random vortex configurations to the energies of the vortex crystal and the fully polarized state, which are the two phases competing with the vortex liquid. We find that the energy of the vortex liquid is lower than those of the vortex crystal and the fully polarized state. For example, see Supplementary Tables 1 and 2, where we provide the energy comparisons between the three states at φ/π = 0.2 and 0.25. Finally, the vortex liquid is more preferable than the ordered states once the temperature becomes finite, due to its large entropy.
Mean-field theory
One may ask what physical properties can be extracted from the classical magnetic vortex liquid. To allow analytical progress, some approximations have to be made. Each random vortex configuration in the vortex liquid is essentially a textured ferromagnet24—the vortices are inhomogeneous spin textures embedded in the background of polarized spins. In other words, most of the spins are nearly or completely aligned with the field, which encourages us to treat the system as the polarized state on average. However, to observe the nontrivial physical effects due to the presence of magnetic vortices, their nonuniform spin textures should somehow be taken into account, at least at the mean-field level. Below, we outline our program in a concise manner, while relaying the details of derivations and calculations to the “Methods” section.
We first start from the polarized state, in which all spins are aligned in the [111] direction, and then incorporate the effect of magnetic vortices in the linear spin wave theory49,50,51, as follows. In general, a smoothly varying spin texture gives rise to a real space Berry phase for magnons hopping on the lattice24,25,26,27. While magnons, unlike electrons and other charged particles, are not coupled to the vector potential of the external magnetic field, they can experience a fictitious gauge field due to the aforementioned Berry phase effect. We elucidate this idea with a judicious choice of the parametrization \(\varphi ={\tan }^{-1}(1/2)\) or K = −2Γ, where the derivation of the effective gauge field greatly simplifies. At such parametrization, all magnon pairings vanishes and the linear spin wave Hamiltonian of the background polarized state reduces to a tight binding model,
Next, we show from the continuum model that the spatial variation of spins in the vortex liquid gives rise to a U(1) gauge field of the form \({A}_{\mu }({\bf{r}})=-\!\cos {\theta }_{{\bf{r}}}{\partial }_{\mu }{\phi }_{{\bf{r}}}\) which couples to the magnons27, similar to how the vector potential couples to the electrons in quantum electrodynamics. Here, μ = x, y, while θr and ϕr are the angles parametrizing the spin orientation at position r. In other words, magnons hopping on the lattice see a fictitious magnetic flux originating from the nonuniform spin textures in the vortex liquid24,25,26. We calculate the total flux of the vortex liquid and spread it uniformly over the lattice. Each vortex carries a flux of −4π, and since the number of vortices and the number of unit hexagons are integers, the flux per unit hexagon is equal to a rational number times the flux quantum, i.e., ϕ = −2πp/q, where p and q are relatively prime.
It is the U(1) gauge field, instead of the fictitious magnetic flux, which couples directly to the magnons hopping on the lattice. Therefore, after making the uniform flux approximation, we have to choose a gauge field A such that the curl ∇ × A produces the uniform flux. To this end, we use the optimal gauge52,53 in which the magnon gains a U(1) phase (via Peierls substitution54,55) of n1ϕ only when hopping along a z bond, where n1 is an integer labeling a site R on the underlying Bravais lattice of the honeycomb lattice along the a1 direction, i.e., R = n1a1 + n2a2. (2) becomes
with i ∈ 0, j ∈ 1, \({{{\Gamma }}}_{ij}={{\Gamma }}\exp (-i{n}_{1}\phi )\) for 〈ij〉 ∈ z, and Γij = Γ for 〈ij〉 ∈ x, y. The lattice curl of the U(1) gauge field for any unit hexagon is (n1 + 1 − n1)ϕ = ϕ, which is exactly what we want. The optimal gauge is illustrated in Fig. 3a. (3) is essentially the bosonic analog of Hofstadter problem55,56,57, which is no longer the problem of a trivial polarized state. If we plot the allowed energy levels as a function of ϕ, we will obtain the Hofstadter butterfly.
a Optimal gauge in which the magnons only gain an additional U(1) phase of n1ϕ when hopping along the z bonds, as indicated by the blue arrows. Such a gauge choice breaks the translational symmetry of the original lattice (with the primitive vectors a1 and a2). The resulting magnetic unit cell contains 2q sublattices for a flux of ϕ = −2πp/q per unit hexagon, where p and q are relatively prime. b Magnon dispersion along high-symmetry directions in the first Brillouin zone, for the vortex liquid at \(\varphi ={\tan }^{-1}(1/2)\) and h/S = 1.3. Since the flux per unit hexagon is ϕ = −2π × 1/50, there are in total 2 × 50 = 100 bands. The bands are nearly flat. Dispersive features are only visible in few bands at intermediate energies.
Magnon energy spectrum
We put the above ideas into action by applying them to a specific example. We consider a sample spin configuration of the vortex liquid at \(\varphi ={\tan }^{-1}(1/2)\) and h/S = 1.3, which has about nine magnetic vortices on a lattice of size L = 30 and a total flux of − 4π × 9 (see Supplementary Fig. 3). Averaging the flux over the lattice, the flux per unit hexagon is ϕ = −4π × 9/302 = −2π × 1/50. Therefore, we have p = 1 and q = 50.
The optimal gauge breaks the translational symmetry by elongating the magnetic unit cell in the a1 direction. Since each magnetic unit cell contains 2q sites, there are in total 2q bands in the reciprocal space. Figure 3b shows the magnon spectrum along a high-symmetry cut in the first Brillouin zone. One immediately sees that the bands are nearly flat—the variation of energy within any band is negligible when compared to the intrinsic energy scale \(\sqrt{{K}^{2}+{{{\Gamma }}}^{2}}=1\). This will simplify the calculation of the thermal Hall conductivity, as discussed in the next subsection.
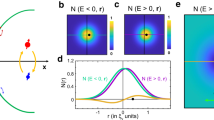
At this stage, we provide a check of the validity and the quality of the mean-field approximation, as follows. We directly apply the real space linear spin wave theory to different random vortex configurations and calculate the magnon densities of states. We find that they only differ slightly from each other, see for example Fig. 4a, b, which suggests that they do not really depend on the precise locations of the vortices. In other words, the individual behavior is similar to the average behavior, see Fig. 4c. Furthermore, the magnon density of states from the real space linear spin wave theory also reveals a huge number of states at low energies, and a dip at intermediate energies. These two features, together with the energy scale, strongly resembles the magnon density of states obtained from the mean-field theory, see Fig. 4d.
Magnon densities of states of a a random vortex configuration and b another, at \(\varphi ={\tan }^{-1}(1/2)\) and h/S = 1.3, on a lattice with 1800 sites, obtained by real space linear spin wave theory. c Magnon density of states obtained by averaging the data from 80 different random vortex configurations like a and b, at the same parameters. d Magnon density of states in the mean-field approximation, at the same parameters, obtained by momentum space linear spin wave theory. Here, we use 100 × 100 k points in the first Brillouin zone defined by the optimal gauge (see Fig. 3a) with p = 1 and q = 50. In a–d, the vertical axis n represents the number of states normalized by the number of sites.
Thermal Hall effect
Once we obtain the magnon spectrum, we can calculate the thermal Hall conductivity, which is given by58,59,60
where V is the total volume of the system, i.e., the total area A times the interlayer distance lc, which we set to be 5 Å (c.f. lc = 5.72 Å in α-RuCl3), \({c}_{2}(x)=(1+x){[\mathrm{ln}\,(1+x)-\mathrm{ln}\,x]}^{2}-{(\mathrm{ln}\,x)}^{2}-2{{\rm{Li}}}_{2}(-x)\) with Li2 being the dilogarithm, \(g(\varepsilon )={[\exp (\varepsilon /{k}_{{\rm{B}}}T)-1]}^{-1}\) is the Bose-Einstein distribution, Ωnk is the reciprocal space Berry curvature of the nth band at momentum k, and Cn is the Chern number of the nth band. In the second equality, we have dropped the term −π2/3, due to the fact that the summation of all Chern numbers is zero61. Furthermore, we have approximated εnk to be constant for a given n, and take the energy at k = 0 as a representative, thus removing the k dependence. This is valid when the temperature scale is much larger than the variation of energy within the thermally populated bands, a condition which always holds in the magnon spectrum under study (see Fig. 3). Lastly, we introduce the thermal Hall conductance \({\kappa }_{xy}^{{\rm{2D}}}={\kappa }_{xy}{l}_{c}\), which is independent of the interlayer distance.
When the field is along the [111] direction, the resulting thermal Hall conductivity is negative. For convenience of comparison to the half-quantized thermal Hall conductance \({\kappa }_{xy}^{{\rm{2D}}}/T=(1/2)(\pi /6)({k}_{{\rm{B}}}^{2}/\hslash )\) due to Majorana fermions1,2,4,62, which is positive, we plot the absolute value ∣κxy∣/T as a function of T, for the vortex liquid at \(\varphi ={\tan }^{-1}(1/2)\) and h/S = 1.3, in Fig. 5. To obtain a positive thermal Hall conductivity, one can reverse the field direction (see the “Methods” section).
The thermal Hall conductivity (in absolute value) due to magnons in the vortex liquid at \(\varphi ={\tan }^{-1}(1/2)\) and h/S = 1.3, as a function of temperature (joined blue dots). The half-quantized thermal hall conductance \({\kappa }_{xy}^{{\rm{2D}}}/T=(1/2)(\pi /6)({k}_{{\rm{B}}}^{2}/\hslash )\) is also indicated (red dashed line) for comparison.
The magnon thermal Hall conductivity is huge already at low temperatures (T/S < 0.1) when compared to the half-quantized value. For example, ∣κxy∣/T = 9.414 × 10−3 WK−2m−1 or \(| {\kappa }_{xy}^{{\rm{2D}}}| /T\approx 5(\pi /6)({k}_{{\rm{B}}}^{2}/\hslash )\) at T/S = 0.07, roughly ten times larger than the half-quantized value. As T increases, ∣κxy∣/T grows and reaches a peak at T/S = 0.2, beyond which it gradually decays, revealing a profile typical in the magnon thermal Hall conductivity. The maximum value of ∣κxy∣/T is about 20 × 10−3 WK−2m−1, which is extraordinarily large, considering the appreciable signals in most thermal transport experiments is of the order 0.1 × 10−3 WK−2m−1. Two factors work together to give a huge thermal Hall conductivity. (i) There are many low lying bands close to the zero energy. In particular, the excitation gap, i.e., the gap between the lowest magnon band and the zero energy, is small. In these bands, the magnon occupation number is significant at low temperatures, resulting in sizable values of the c2 function. (ii) The lowest 36 bands in the magnon spectrum have the same Chern number Cn = 1. The energy scale of the 36th band is roughly 0.9S. For T/S < 0.9, the bands with index n > 36 are not of much relevance as they are not thermally populated, resulting in small values of the c2 function. On the other hand, by the approximation in (4), the values of the c2 function for the bands with index n < 36 add up constructively as they have the same Chern number. In contrast, if the Chern number alternates between +1 and −1 as the band index n increases, the values of c2 function weighted by Cn will tend to cancel out, leading to a small thermal Hall conductivity. Finally, we would like to comment on the temperature scale in Fig. 5. One may worry about strong thermal fluctuations of the vortex density at high temperatures. However, in this work, we focus on the low-temperature regime where we can assume the vortex density to be constant. Since the energies of the classical spin configurations with different vortex densities scale as S2, while the temperatures in Fig. 5 scale as S, under the large S assumption in our semiclassical approach, the temperature scale under study can in principle be low enough to assume a constant vortex density.
One may ask what can be expected for the thermal Hall conductivity of the vortex liquids at other parameters than \(\varphi ={\tan }^{-1}(1/2)\). For generic φ, it is difficult to obtain an explicit expression for the gauge field and subsequently develop a framework to calculate the thermal Hall conductivity. Nonetheless, we can extend the mean-field theory of the vortex liquid at \(\varphi ={\tan }^{-1}(1/2)\approx 0.15\pi\) to its neighborhood, as follows. For φ close to \({\tan }^{-1}(1/2)\), the linear spin wave Hamiltonian of the background polarized spins has small magnon pairings in addition to dominant magnon hoppings. In the mean-field theory, the hopping terms can be approximated by the tight binding model subjected to the previously derived U(1) gauge field as in (3), while the pairing terms are weighted by the factors \(\pm \,(K+2{{\Gamma }})/2\sqrt{3}\). We now have a Bogoliubov de Gennes Hamiltonian of magnons, from which we can calculate the dispersion and the thermal Hall conductivity. We apply the extended mean-field theory to the vortex liquids at φ/π = 0.13 and 0.14, where we find that the magnon dispersion remains more or less the same as in the case of \(\varphi ={\tan }^{-1}(1/2)\) and yields a thermal Hall conductivity of the same magnitude. See Supplementary Note 3 for details. On the other hand, for φ not close to \({\tan }^{-1}(1/2)\), for example φ/π = 0.2 and 0.25, we can calculate the magnon densities of state directly from the real space spin configurations of random vortices. They reveal a considerable number of low lying states, which is suggestive of a large thermal Hall conductivity. See Supplementary Note 4 for details.
Specific heat
With the classical magnetic vortex liquid being a hugely degenerate ensemble of vortex configurations at zero temperature, it resembles our understanding of a classical spin liquid. However, such an intricate degeneracy is often lifted by entropic corrections at finite temperatures, a mechanism known as order by disorder63. In order to investigate the stability of vortex liquid in the presence of thermal fluctuations, we perform finite temperature Monte Carlo simulations of the classical spin model (1).
We confirm that the vortex liquid exists as a thermal ensemble at finite temperatures. Also, in the parametric regime where a dilute vortex liquid is stabilized, the specific heat as a function of temperature does not show any sign of a thermal phase transition. The specific heat at φ = π/4 and h/S = 0.95 is displayed in Fig. 6b for three different system sizes. The data shows no dependence on the system size, which suggests the absence of finite-size effect in the dilute vortex liquid. The transition into the vortex liquid state is rather a smooth crossover than a conventional phase transition. In contrast, the finite extent of the system becomes relevant when the density of vortices increases. At h/S ≲ 0.9 the specific heat acquires a system-size dependence, with cusps in the specific heat curve indicating the onset of vortex crystallization as shown in Fig. 6a for h/S = 0.85.
a At h/S = 0.85, system-size dependent cusps around T/S2 = 0.03 indicate strong finite-size effects and vortex crystallization. b In the vortex liquid regime at h/S = 0.95, where vortices become dilute, the curves for different system sizes coincide and finite-size effects are not observed. Both datasets are obtained at φ = π/4 for different system sizes L = 18, 24, 30. Statistical error bars are smaller than the plot markers.
Since the vortex crystal is periodic in real space, the magnon dispersion can be simply obtained by a Fourier transformation, which then allows us to calculate the thermal Hall conductivity. We find that ∣κxy∣/T is of the order 1 × 10−3 WK−2m−1, which is larger than typical signals, but still dwarfed by the thermal Hall conductivity of the vortex liquid. See Supplementary Note 6 for details.
Equal-time spin correlator
We would like to identify signatures of the classical magnetic vortex liquid from the two-spin correlation functions. First, we calculate the equal-time spin correlator
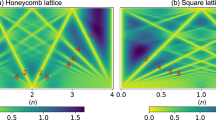
We anticipate that at the Brillouin zone center (i.e., the Γ point), the dominant contribution scales with the total number of sites, since the majority of spins are polarized. Furthermore, we expect subleading intensity to emerge at some characteristic momentum scale ∣qvortex∣, which corresponds to the typical inter-vortex distance in real space. Indeed, as shown in Fig. 7b for φ = π/4 and h/S = 0.95, such an accumulation of intensity can be observed; the subdominant correlations appear as a ring-like feature around the dominant peak at the Γ point. The isotropic nature of this intensity distribution signals that there is no long-range order beyond the characteristic momentum scale, which reflects our definition of the vortex liquid as a thermal ensemble of random vortex configurations. This is in stark contrast to the signature of the vortex crystal phase, where sharp peaks in the equal-time spin correlator indicate long-range order (Fig. 7a for φ = π/4 and h/S = 0.85). Moreover, the characteristic momentum ∣qvortex∣ described by these peaks is larger than the characteristic momentum in the vortex liquid regime, since the real space vortex distance in the vortex crystal is shorter.
The data is obtained at φ = π/4 and L = 24 in the low-temperature regime T/S2 = 0.02. a Correlations in the vortex crystal phase at h/S = 0.85 plotted within the first Brillouin zone. In addition to the leading peak at the Γ point, which extends up to \({\mathcal{O}}(1{0}^{3})\) and reflects a strong ferromagnetic correlation, the presence of sharp, subleading peaks indicates a periodic vortex arrangement. Color scale shown is in the range [0, 30]. b In the vortex liquid phase at h/S = 0.95, subleading intensity accumulates isotropically at a characteristic distance from the Γ point, reflecting the typical inter-vortex distance in real space. Color scale shown is in the range [0, 0.5].
Dynamical spin structure factor
Finally, we compute the dynamical spin structure factor to extract information on the excitation spectrum. To achieve this, we consider spin configurations from the thermal ensemble generated in the Monte Carlo simulations and determine their time evolutions under the classical Landau–Lifshitz equations of motion. An animation of such a time evolution can be found in the Supplementary Video. A subsequent Fourier transform leads to the dynamical spin structure factor
As in the equal-time spin correlator, we expect to see dominant ferromagnetic correlations and the corresponding magnon dispersion (with two branches) in the dynamical spin structure factor. The presence of magnetic vortices further imprints subleading flat bands, as shown in Fig. 8a for φ = π/4 and h/S = 0.95. The intensities from these flat bands smoothly blend into the background, resembling a continuum of spin excitations. For comparison, the dynamical structure factor of the fully polarized state is shown in Fig. 8b, which reveals two distinctive branches of magnon dispersion.
The data is obtained at φ = π/4, L = 24, and plotted at T/S2 = 0.02. a The field h/S = 0.95 gives rise to a dilute vortex liquid. b In the fully polarized state at h/S = 1.0 only the two conventional magnon bands are visible. Note that the leading ω = 0 divergence at the Γ point gives rise to an unphysical tail at ω > 0, which is a numerical artifact of the Fourier transform over a finite time interval (see the Methods section for details).
Notably, the resulting dynamical spin structure factor, which we obtained for the thermodynamic ensemble, closely resembles that obtained for just one random vortex configuration, suggesting that the precise locations of vortices have negligible effects. This is further corroborated by the observation that the vortices remain localized as time evolves. They do not move around on the lattice, while thermally excited defects propagate through the spins, see Fig. 9. Therefore, the diffuse, flat-band features in the dynamical spin structure factor likely originate from magnons in the background polarized state experiencing the average gauge field of the vortex spin textures. This is also in line with our assumption that the heat carriers responsible for the thermal Hall effect are magnons in the background polarized state, but not the vortices.
It is thus not surprising that we find striking similarities between the dynamical spin structure factor measured in the Monte Carlo simulations and that calculated in our mean-field theory approach (see Supplementary Fig. 14). These similarities include (i) the emergence of a continuum of flat bands, (ii) the absence of signals at intermediate energies around the Γ point, and (iii) stronger (weaker) signals around the upper (lower) branch of the magnon dispersion.
Relevance to real materials
There exists a self-dual transformation \({{\mathcal{T}}}_{1}\) of the \(JK{{\Gamma }}{{\Gamma }}^{\prime}\) model, under which all spins are rotated uniformly by π about the [111] direction40. Here we apply \({{\mathcal{T}}}\!_{1}\) to the KΓ model with K > 0 and Γ < 0 investigated in this work. The parameters in the rotated frame are given by \(\tilde{J}=4K/9-4{{\Gamma }}/9,\tilde{K}=-K/3+4{{\Gamma }}/3,\tilde{{{\Gamma }}}=4K/9+5{{\Gamma }}/9\), and \(\tilde{{{\Gamma }}}^{\prime} =-2K/9+2{{\Gamma }}/9\), such that the sign of the Kitaev interaction \(\tilde{K}\) is always negative, while that of \(\tilde{{{\Gamma }}}\) is positive for ∣Γ/K∣ < 4/5. Such a sign structure is the same as that in α-RuCl341,42,43,44,45 and similar materials. Meanwhile, the [111] field remains invariant under \({{\mathcal{T}}}_{1}\) since it lies exactly along the rotation axis.
α-RuCl3 has dominant \(\tilde{K}\,<\,0\) and \(\tilde{{{\Gamma }}}\,>\,0\) interactions with \(| \tilde{K}/\tilde{{{\Gamma }}}| \approx 2\)41,43,44. On top of these, other interactions such as \(\tilde{J}\), \(\tilde{{{\Gamma }}}^{\prime}\) and/or \({\tilde{J}}_{3}\) at the subleading order are present, so that the zigzag (ZZ) magnetically ordered state is stabilized in the zero field limit, as observed in experiments13,46. We investigate the extent of the classical magnetic vortex liquid towards more realistic model parameters, as follows. First, we choose ∣K/Γ∣ = 22/5 (or \(\varphi ={\tan }^{-1}(5/22)\approx 0.07\pi\)) in (1) such that \(| \tilde{K}/\tilde{{{\Gamma }}}| =2\) in the dual model. However, the corresponding \(\tilde{J}\) and \(\tilde{{{\Gamma }}}^{\prime}\) are quite significant. We then continuously deform the dual model to one in which \(\tilde{J}\) and \(\tilde{{{\Gamma }}}^{\prime}\) vanish. More precisely, we introduce a tunable parameter ξ ∈ [0, 1] such that (i) at ξ = 0, the set of parameters \(\{\tilde{J},\tilde{K},\tilde{{{\Gamma }}},\tilde{{{\Gamma }}}^{\prime} \}\) is mapped from (1) with \(\varphi ={\tan }^{-1}(5/22)\) under \({{\mathcal{T}}}_{1}\), (ii) at ξ = 1, \(\tilde{J}=0\), \(\tilde{{{\Gamma }}}^{\prime}\)=0, and \(\sqrt{{\tilde{K}}^{2}+{\tilde{{{\Gamma }}}}^{2}}=1=\sqrt{{K}^{2}+{{{\Gamma }}}^{2}}\), and (iii) the ratio \(| \tilde{K}/\tilde{{{\Gamma }}}| =2\) is kept fixed throughout the deformation. The Hamiltonian describing the deformation can be found in Supplementary Note 7. We indicate the extent of the vortex liquid as ξ is increased from 0 to 1 in Fig. 10.
We continuously deform the dual model of the KΓ model with K > 0 and Γ < 0 to models that are relevant to α-RuCl3 and similar materials, by tuning ξ from 0 to 1. We find a significant extent of the classical magnetic vortex liquid to large values of ξ, where the ground state in the low-field regime is the ZZ order.
Remarkably, the vortex liquid survives up to ξ ≈ 0.8. Although the structure of vortex greatly simplifies beyond ξ ≈ 0.2, the fluid-like nature remains—the vortices do not form a crystalline order, but they appear at rather random positions in the background of polarized spins (see Supplementary Figs. 12 and 13). On the other hand, the ground state at zero and low fields for 0.5 ≲ ξ ≲ 0.9 is the ZZ order. Considering the set of parameters for ξ ≳ 0.5 as realistic, our result suggests that the vortex liquid may be relevant to real materials like α-RuCl3 at high fields.
Discussion
Considering frustrated honeycomb magnets with bond-dependent interactions, we unveil the classical magnetic vortex liquid state in the presence of an external magnetic field. The magnetic vortices are textures made out of a large number of spins and embedded in the background of polarized spins. Instead of settling in a crystalline order, the vortices form a liquid state, while distinct configurations of the vortices form a thermal ensemble. We show that this novel phase leads to a continuum of spin excitations that can be seen in neutron scattering experiments and a large thermal Hall conductivity.
Furthermore, we investigate the relevance of the vortex liquid to existing Kitaev materials like α-RuCl3 by continuously evolving the dual model of (1) towards more realistic models41,43,44. We establish the survival of the vortex liquid at realistic interaction parameters, where the ground state in the low-field regime is the ZZ order. Our result suggests the possible existence of the vortex liquid phase in real materials. However, the highest magnetic fields (e.g., ~60 T in ref. 46) that can be applied in experiments have so far failed to polarize α-RuCl3 in the [111] direction. One may look for other Kitaev materials with spin interactions at a lower energy scale, such as f-electron-based honeycomb magnets64, so that the polarized state and hence the vortex liquid are practically accessible under a [111] field.
Nonetheless, it is interesting to see that the spin excitation continuum and the large thermal Hall conductivity discovered in the vortex liquid state are reminiscent of the experimental observations in α-RuCl3. There is an important difference, though, between our work and established experiments, in terms of field direction. Most of the relevant experiments on α-RuCl3 were carried out under in-plane and tilted magnetic fields. That is, the neutron scattering continuum is observed in the presence of a magnetic field parallel to the honeycomb plane65,66,67, while the half-quantized thermal Hall conductivity was discovered in magnetic fields tilted away from the [111] direction and along certain in-plane direction1,2. Our model, on the other hand, would be more relevant to future experiments with the [111] magnetic field. We remark that although our semiclassical analysis is strictly valid in the large S limit, it remains to be seen to what extent our results can be applied to quantum S = 1/2 systems, which will be an interesting direction for future experimental studies.
Finally, we discuss the relation of our work to existing theoretical studies. A classical phase diagram in the low-field regime h/S ∈ [0, 0.2] of the same model (1) has recently been reported in ref. 68, which used an unsupervised machine learning method. The classical magnetic vortex liquid is not relevant at such low fields as it only occupies a tiny area. Moreover, it may be difficult for unsupervised machine learning to give an appropriate interpretation to an inhomogeneous state in which the majority of spins are still polarized. These are the possible reasons that the vortex liquid was not identified in ref. 68.
On the other hand, the quantum model of (1) has recently been investigated using the density matrix renormalization group (DMRG) on the two-leg ladder system69. Among the plethora of phases presented in the phase diagram, the uniform chirality (UC) phase and the staggered chirality (SC) phase, where the scalar spin chirality is finite, could be related to the vortex liquid in our work. This is because the noncoplanar spin structure of each vortex gives rise to a finite scalar spin chirality. The precise connection, however, is not clear at the moment. The fate of the vortex liquid in the quantum model will be an important and interesting subject of future study.
Methods
Mean-field theory
Here, we provide technical justifications to the mean-field approach adopted in this study, which ultimately leads to an effective description of the vortex liquid as the bosonic analog of Hofstadter problem. Since it involves multiple steps with different concepts, we organize the content in five parts, as follows.
First, our starting point is the application of linear spin wave theory49,50 to the field polarized state of (1), in which all spins are aligned in the [111] direction. We perform a (global) coordinate transformation such that the z-axis of the new coordinate system is along the [111] direction. Moreover, we fix the x and y directions to be \([11\bar{2}]\) and \([\bar{1}10]\) respectively. The spin \({\tilde{{\bf{S}}}}_{i}\) as measured in the new basis is related to Si by \({{\bf{S}}}_{i}=R{\tilde{{\bf{S}}}}_{i}\), where
If we define
the spin Hamiltonian (1) in the rotated basis is then \(H=\mathop{\sum }\limits_{\lambda }\mathop{\sum }\limits_{\langle ij\rangle \in \lambda }{\tilde{{\bf{S}}}}_{i}^{{\rm{T}}}{\tilde{H}}_{\lambda }{\tilde{{\bf{S}}}}_{j}-\mathop{\sum }\limits_{i}\tilde{{\bf{h}}}\cdot {\tilde{{\bf{S}}}}_{i}\), where \({\tilde{H}}_{\lambda }={R}^{{\rm{T}}}{H}_{\lambda }R\) and \(\tilde{{\bf{h}}}={R}^{{\rm{T}}}{\bf{h}}\). We then carry out the Holstein Primakoff transformation,
and keep only terms up to second order in b. At the rather special parametrization K = −2Γ, the rotated Hamiltonian components are, explicitly,
such that all magnon pairings vanish at the level of linear spin wave theory, yielding a Hamiltonian which is in essence the tight binding model of magnons (2), where Γ assumes the role of hopping integral and h assumes the role of mass. Furthermore, (2) is exactly identical to the linear spin wave Hamiltonian of the XY model in a field along the z-axis, with the spin exchange J = −Γ.
We make a remark concerning the nonvanishing matrix elements in (10) which connect the x or y component of one spin to the z component of the other, e.g. \(-{{\Gamma }}/\sqrt{2}\) or \(\sqrt{3/2}{{\Gamma }}\) in \({\tilde{H}}_{x}\). They will generate terms linear in b. However, as explained in ref. 50, the coefficients of these linear terms vanish, due to \(\partial H/\partial \tilde{{\bf{S}}}{| }_{\tilde{{\bf{S}}} = (0,0,S)}\) in the classical ground state (or any local minimum).
Second, we derive the continuum version of the Hamiltonian (1) and, through a series of approximations, reduce it to the form of an XY model. For simplicity, we drop the Zeeman term as it does not affect the following analysis.
Assume that site i belongs to sublattice 0. Up to some constant, the Kitaev interaction can be rewritten as
where nλ=x,y,z denote the three bond directions. This should only be taken as a shorthand notation though, because there are really just two independent directions in the two dimensional lattice. As will be argued later, the effective low-energy theory is isotropic in the two dimensional space (resembling an XY model), so we should not worry too much about three nλ at this point. One can show that the corresponding expression for i ∈ 1 is same as (11) due to the gradient term being squared. Similarly, the Γ interaction can be rewritten as
where (λ, μ, ν) is a cyclic permutation of (x, y, z). Again, one can show that the corresponding expression for i ∈ 1 is same as (12). We further neglect the on-site interaction \({S}_{{\bf{r}}}^{\mu }{S}_{{\bf{r}}}^{\nu }\) based on the following argument. In the classical limit S ⟶ ∞, we are allowed to symmetrize such a term as \((1/2)({S}_{{\bf{r}}}^{\mu }{S}_{{\bf{r}}}^{\nu }+{S}_{{\bf{r}}}^{\nu }{S}_{{\bf{r}}}^{\mu })\), but this becomes zero in the quantum limit S = 1/2 since different components of the spin operator anticommute.
Written more compactly, the continuum KΓ model is thus
Given a generic spin configuration {Sr}, let Rr ∈ SO(3) be the rotation matrix that defines the local coordinate frame, i.e., \({{\bf{S}}}_{{\bf{r}}}={R}_{{\bf{r}}}{\tilde{{\bf{S}}}}_{{\bf{r}}}\) and \({\tilde{{\bf{S}}}}_{{\bf{r}}}=(0,0,S)\). Let Sr be parametrized by two angles θr and ϕr as \({{\bf{S}}}_{{\bf{r}}}=S(\sin {\theta }_{{\bf{r}}}\cos {\phi }_{{\bf{r}}},\sin {\theta }_{{\bf{r}}}\sin {\phi }_{{\bf{r}}},\cos {\theta }_{{\bf{r}}})\). We choose Rr to be27,50
We will make the spatial dependence of θ and ϕ implicit by dropping the subscript r. It can be easily verified that (7) corresponds to (14) with \(\theta ={\cos }^{-1}(1/\sqrt{3})\) and ϕ = π/4. Switching to the local coordinate frame, (13) becomes
where \({\nabla }_{\lambda }({\bf{r}})={\partial }_{{{\bf{n}}}_{\lambda }}+{R}_{{\bf{r}}}^{{\rm{T}}}{\partial }_{{{\bf{n}}}_{\lambda }}{R}_{{\bf{r}}}\) and \({\tilde{H}}_{\lambda }({\bf{r}})={R}_{{\bf{r}}}^{{\rm{T}}}{H}_{\lambda }{R}_{{\bf{r}}}\). Since we are considering a textured ferromagnet, where most spins deviate only slightly from the [111] direction, we replace the local Hamiltonian \({\tilde{H}}_{\lambda }({\bf{r}})\) by a global one, \({\tilde{H}}_{\lambda }({\bf{r}})\approx {R}^{{\rm{T}}}{H}_{\lambda }R\equiv {\tilde{H}}_{\lambda }\) with R given in (7). However, we still allow smooth spatial variation of Rr in ∇λ(r).
At K = −2Γ, \({\tilde{H}}_{\lambda }\) is given by (10). We further approximate the low-energy physics of the textured ferromagnet as the XY model, i.e., \({\tilde{H}}_{\lambda }\approx {H}_{{\rm{XY}}}={\rm{diag}}(-{{\Gamma }},-{{\Gamma }},0)\). Heuristically, this is possible because the linear spin wave theory of the KΓ model at such parametrization is equivalent to that of the XY model, which we justify as follows. For small deviations from the polarized state, following the discussion in the previous subsection, the contributions to the resulting linear spin wave Hamiltonian from the \({S}_{i}^{x}{S}_{j}^{z}\) and \({S}_{i}^{y}{S}_{j}^{z}\) terms are insignificant, which motivates us to set the corresponding matrix elements to 0. This additional simplification allow us to treat the effect of inhomogeneous spin textures as a U(1) gauge field, as discussed below.
Third, we demonstrate that the inhomogeneous spin textures in the vortex liquid gives rise to a fictitious magnetic flux which will be experienced by the magnons. From (14), we have27
Substituting (16) into (15) with \({\tilde{H}}_{\lambda }({\bf{r}})\approx {H}_{{\rm{XY}}}\), and performing the Holstein Primakoff transformation (9),
where we have neglected terms quadratic in the derivative of the local spin structure, as well as terms linear in b (which describe the interaction between magnons and the local spin structure)27. In the second equality, the integrand has the same expression in all bond directions λ = x, y, z, so we may as well replace nλ by μ = x, y. We see that the effect of local rotation enters as a U(1) gauge field \({A}_{\mu }=-\!\cos \theta {\partial }_{\mu }\phi\) that couples to the magnons, which is twice as large as that for conduction electrons hopping in a nonuniform spin background26,29. In other words, the magnons experience a fictitious magnetic flux due to the U(1) gauge field which originates from the spatial variation of spins in the vortex liquid.
Fourth, to calculate the fictitious magnetic flux ϕ of some area A, we take the curl of the gauge field obtained in the previous subsection
and integrate it over A, which is equal to the solid angle subtended by the spins around the boundary ∂A70. Returning to the discrete model (i.e., lattice), we want to calculate the flux penetrating each unit hexagon. To achieve this, we partition each unit hexagon into four triangles (see Supplementary Fig. 15a, b for instance), and add up the solid angles of these triangles according to the formula71,72
Imagine that a magnon hops around these triangles, say, in the anticlockwise sense, the U(1) phases gained along the internal lines will cancel (up to an additive factor of 2π) as they are traveled exactly once along opposite directions. The summation of solid angles under different partitionings of the unit hexagon differ by an integer multiple of 4π, which has no physical consequence (e4πi = 1).
We fix the range of flux per hexagon to be [ −2π, 2π). One may argue that any interval of length 4π, for example [0, 4π), are equally valid, which is true if we do not average the flux over the lattice. Since we are planning elsewise, we justify why the choice of [−2π, 2π) is more physical than others as follows.
The total flux (i.e., summation of the fluxes of all hexagons) is an integer multiple of 2π, which is consistent with the U(1) gauge theory. This is because each nearest bond is traveled exactly once along opposite directions. By restricting the flux per hexagon between −2π and 2π when we are evaluating (19), the total flux is equal to −4π multiplied by the total number of vortices, a feature that does not generally hold for other intervals. Also, the spatial gradient of the local spin structure is small in a textured ferromagnet, so the fluxes of most unit hexagons should be close to zero. It makes more sense to assign to a unit hexagon a flux of +ϵ or −ϵ, rather than ϵ or 4π −ϵ for instance, where ϵ is some small positive real number. We emphasize again that we have to carefully choose the range of flux per unit hexagon only because we are going to average the flux over the lattice. If we were not to do so, then we would be satisfied with any interval of length 4π.
Suppose that there are \(n\in {\mathbb{N}}\) vortices such that the total flux of the vortex liquid is −4πn, and the system has a total number of N unit hexagons. We then spread the total flux uniformly over the system, so the flux of each unit hexagon is −4πn/N = −2πp/q, where p and q are relatively prime. This is reminiscent of the famous Hofstadter problem in which electrons hopping on a lattice are subjected to a uniform magnetic field, as discussed in the “Results” section.
Finally, after averaging the fictitious magnetic flux, we attach the U(1) gauge field (of the optimal gauge) to the magnons in the polarized state, which yields the bosonic Hofstadter model. Since a series of approximations have been made, we have to slightly tune the magnetic field h in (3) or we risk getting an unstable spectrum with negative energies. For instance, we cannot use h/S = 1.3 directly in (3) for ϕ = −2π × 1/50, even though the corresponding spin configuration is obtained at h/S = 1.3. To resolve this issue, we set h to be the critical field hcrit = 3∣Γ∣ at which the system is fully polarized, which is a reasonable choice because the vortex liquid takes place near the polarized regime. At the critical field, the zero flux magnon spectrum (i.e., the simple polarized state neglecting any effect of the inhomogeneous spin texture) is exactly gapless, but a finite flux like ϕ = −2π × 1/50 induces a small gap stabilizing the magnon spectrum.
Evaluation of Chern number
As shown in (4) in the “Results” section, we need the Chern numbers of the magnon bands to calculate the thermal Hall conductivity. Here, we elaborate on how to evaluate the Chern number for a given band.
If the nth band is nondegenerate, the Berry connection, Berry curvature, and Chern number are given, respectively, as23,29,73
where \(\left|n{\bf{k}}\right\rangle\) is the (normalized) eigenstate corresponding to the eigenvalue εnk, μ, ν = x, y, FBZ denotes the first Brillouin zone, and in the last equality we have switched from the continuum integral to the discrete summation with A denoting the total area of the system (not to be confused with the Berry connection or the gauge field).
If the nth band is M-fold degenerate, the Chern number is defined collectively for the degenerate manifold as follows. We first define the multiplet \({\psi }_{{\bf{k}}}=(\left|{n}_{1}{\bf{k}}\right \rangle,\ldots ,\left|{n}_{M}{\bf{k}}\right \rangle)\). The (nonabelian) Berry connection, Berry curvature, and Chern number are given, respectively, as73,74,75
where d is the differential operator such that Ak is a differential 1-form and Ωk is a differential 2-form.
For ϕ = −2π × 1/50 describing the vortex liquid at \(\varphi ={\tan }^{-1}(1/2)\) and h/S = 1.3, we check the convergence of each Chern number to an integer with increasing momentum grids in the first Brillouin zone, and that the summation of all Chern numbers is zero, \(\mathop{\sum }\nolimits_{n = 1}^{2q}{C}_{n}=0\). We find that 72 out of 2q = 100 bands in the magnon spectrum (see Fig. 3) carry Chern number 1, while the largest Chern number is 51. None of the bands have Chern number 0, signifying their topological nontriviality.
While most of the bands at low and high energies are nondegenerate, some bands at intermediate energies (roughly between ω/S = 1 and 2) are two fold degenerate. Strictly speaking, the formula (4) is derived only for nondegenerate bands, but the second equality in (4) suggests that we can treat an M-fold degenerate band as a single band with a collective Chern number Cψ.
Finally, we remark on the how the Chern numbers change when we invert the magnetic field. When the field is along the [111] direction, the ground state spin configuration is {Si}, the flux carried by each vortex is negative, so is the total flux. The corresponding set of Chern numbers {Cn} yields a negative thermal Hall conductivity. When the field is along the \([\bar{1}\bar{1}\bar{1}]\) direction, the ground state spin configuration changes as {Si} ⟶ {−Si}. Meanwhile, the linear spin wave Hamiltonian of the background polarized state under the \([\bar{1}\bar{1}\bar{1}]\) field is the same as that under the [111] field. Therefore, we still obtain the vortex liquid under h ⟶ −h as long as the field magnitude remains the same, yet each vortex has an opposite chirality-the flux carried by each vortex is now positive, and the resulting set of Chern numbers changes as {Cn} ⟶ {−Cn}. By (4), the thermal Hall conductivity flips sign and is now positive.
Finite temperature Monte Carlo simulations
In order to access the thermal properties of the classical spin model defined in Eq. (1), we resort to finite temperature Monte Carlo simulations. We perform the simulations on lattices with L × L unit cells (or N = L × L × 2 sites) with periodic boundary conditions, typically at L = 24. We equilibrate the simulations for 107 sweeps, where a single sweep amounts to N attempted local spin updates, before taking measurements for an additional 108 sweeps. To improve the convergence of the simulation, we employ a parallel tempering technique to simultaneously equilibrate systems at 96 different temperatures, which are logarithmically spaced between \({T}_{\min }=0.02\) and \({T}_{\max }=1\).
For the calculation of the spin correlations and the dynamical spin structure factor, we process one spin configuration every 2000 sweeps, i.e., a total of 50,000 configurations generated throughout the Monte Carlo simulation. The time evolution of every individual spin configuration is obtained by solving the Landau–Lifshitz equation76,77
(with cyclic permutations of x, y, and z, assuming unit spins), where iλ indicates the nearest neighbor connected to i via the λ ∈ {x, y, z} bond. (22) is solved numerically up to a time \({t}_{\max }=500\), with a dynamic step size and a local error tolerance chosen to produce convergent results at least up to \({t}_{\max }\)78,79. The structure factor is then obtained by Fourier transforming the time evolution of spins (in steps of Δt = 0.05) and subsequent thermal averaging over all 50,000 configurations.
Data availability
All relevant data in this paper are available from the authors upon reasonable request.
Code availability
All numerical codes in this paper are available from the authors upon reasonable request.
References
Kasahara, Y. et al. Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid. Nature 559, 227–231 (2018).
Yokoi, T. et al. Half-integer quantized anomalous thermal Hall effect in the Kitaev material α-RuCl3. Preprint at https://arxiv.org/abs/2001.01899 (2020).
Grissonnanche, G. et al. Giant thermal hall conductivity in the pseudogap phase of cuprate superconductors. Nature 571, 376–380 (2019).
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Vinkler-Aviv, Y. & Rosch, A. Approximately quantized thermal Hall effect of chiral liquids coupled to phonons. Phys. Rev. X 8, 031032 (2018).
Ye, M., Halász, G. B., Savary, L. & Balents, L. Quantization of the thermal Hall conductivity at small Hall angles. Phys. Rev. Lett. 121, 147201 (2018).
Ye, M., Fernandes, R. M. & Perkins, N. B. Phonon dynamics in the kitaev spin liquid. Phys. Rev. Res. 2, 033180 (2020).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: From Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Rau, J. G., Lee, E. K.-H. & Kee, H.-Y. Generic spin model for the honeycomb iridates beyond the Kitaev limit. Phys. Rev. Lett. 112, 077204 (2014).
Takagi, H., Takayama, T., Jackeli, G., Khaliullin, G. & Nagler, S. E. Concept and realization of Kitaev quantum spin liquids. Nat. Rev. Phys. 1, 264–280 (2019).
Janssen, L. & Vojta, M. Heisenberg-Kitaev physics in magnetic fields. J. Phys.: Condens. Matter 31, 423002 (2019).
Plumb, K. W. et al. α-RuCl3: A spin-orbit assisted Mott insulator on a honeycomb lattice. Phys. Rev. B 90, 041112 (2014).
Sears, J. A. et al. Magnetic order in α-RuCl3: a honeycomb-lattice quantum magnet with strong spin-orbit coupling. Phys. Rev. B 91, 144420 (2015).
Chaloupka, J., Jackeli, G. & Khaliullin, G. Kitaev-Heisenberg model on a honeycomb lattice: Possible exotic phases in iridium oxides A2IrO3. Phys. Rev. Lett. 105, 027204 (2010).
Katukuri, V. M. et al. Kitaev interactions between j = 1/2 moments in honeycomb Na2IrO3 are large and ferromagnetic: insights from ab initio quantum chemistry calculations. New J. Phys. 16, 013056 (2014).
Chun, S. H. et al. Direct evidence for dominant bond-directional interactions in a honeycomb lattice iridate Na2IrO3. Nat. Phys. 11, 462–466 (2015).
Hickey, C. & Trebst, S. Emergence of a field-driven U(1) spin liquid in the Kitaev honeycomb model. Nat. Commun. 10, 530 (2019).
Kaib, D. A. S., Winter, S. M. & Valentí, R. Kitaev honeycomb models in magnetic fields: dynamical response and dual models. Phys. Rev. B 100, 144445 (2019).
Jiang, H.-C., Wang, C.-Y., Huang, B. & Lu, Y.-M. Field induced quantum spin liquid with spinon Fermi surfaces in the Kitaev model. Preprint at https://arxiv.org/abs/1809.08247 (2018).
Dasgupta, S., Zhang, S., Bah, I. & Tchernyshyov, O. Quantum statistics of vortices from a dual theory of the XY ferromagnet. Phys. Rev. Lett. 124, 157203 (2020).
Baskaran, G., Sen, D. & Shankar, R. Spin-S Kitaev model: Classical ground states, order from disorder, and exact correlation functions. Phys. Rev. B 78, 115116 (2008).
Rousochatzakis, I. & Perkins, N. B. Classical spin liquid instability driven by off-diagonal exchange in strong spin-orbit magnets. Phys. Rev. Lett. 118, 147204 (2017).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57 (1984).
Dugaev, V. K., Bruno, P., Canals, B. & Lacroix, C. Berry phase of magnons in textured ferromagnets. Phys. Rev. B 72, 024456 (2005).
van Hoogdalem, K. A., Tserkovnyak, Y. & Loss, D. Magnetic texture-induced thermal Hall effects. Phys. Rev. B 87, 024402 (2013).
Oh, Y.-T., Lee, H., Park, J.-H. & Han, J. H. Dynamics of magnon fluid in Dzyaloshinskii-Moriya magnet and its manifestation in magnon-Skyrmion scattering. Phys. Rev. B 91, 104435 (2015).
Tatara, G. Effective gauge field theory of spintronics. Phys. E (Amsterdam, Neth.) 106, 208–238 (2019).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Everschor-Sitte, K. & Sitte, M. Real-space Berry phases: Skyrmion soccer (invited). J. Appl. Phys. 115, 172602 (2014).
Kawano, M. & Hotta, C. Discovering momentum-dependent magnon spin texture in insulating antiferromagnets: role of the Kitaev interaction. Phys. Rev. B 100, 174402 (2019).
Katsura, H., Nagaosa, N. & Lee, P. A. Theory of the thermal Hall effect in quantum magnets. Phys. Rev. Lett. 104, 066403 (2010).
Onose, Y. et al. Observation of the magnon Hall effect. Science 329, 297–299 (2010).
Ideue, T. et al. Effect of lattice geometry on magnon Hall effect in ferromagnetic insulators. Phys. Rev. B 85, 134411 (2012).
Owerre, S. A. Topological honeycomb magnon Hall effect: a calculation of thermal Hall conductivity of magnetic spin excitations. J. Appl. Phys. 120, 043903 (2016).
Owerre, S. A. Magnon Hall effect in AB-stacked bilayer honeycomb quantum magnets. Phys. Rev. B 94, 094405 (2016).
Owerre, S. A. Topological magnon bands and unconventional thermal Hall effect on the frustrated honeycomb and bilayer triangular lattice. J. Phys.: Condens. Matter 29, 385801 (2017).
Owerre, S. Topological thermal Hall effect due to Weyl magnons. Can. J. Phys. 96, 1216–1223 (2018).
McClarty, P. A. et al. Topological magnons in Kitaev magnets at high fields. Phys. Rev. B 98, 060404 (2018).
Hwang, K., Trivedi, N. & Randeria, M. Topological magnons with nodal-line and triple-point degeneracies: implications for thermal Hall effect in pyrochlore iridates. Phys. Rev. Lett. 125, 047203 (2020).
Chaloupka, J. & Khaliullin, G. Hidden symmetries of the extended Kitaev-Heisenberg model: Implications for the honeycomb-lattice iridates A2IrO3. Phys. Rev. B 92, 024413 (2015).
Kim, H.-S. & Kee, H.-Y. Crystal structure and magnetism in α-RuCl3: An ab initio study. Phys. Rev. B 93, 155143 (2016).
Winter, S. M., Li, Y., Jeschke, H. O. & Valentí, R. Challenges in design of Kitaev materials: magnetic interactions from competing energy scales. Phys. Rev. B 93, 214431 (2016).
Wang, W., Dong, Z.-Y., Yu, S.-L. & Li, J.-X. Theoretical investigation of magnetic dynamics in α-RuCl3. Phys. Rev. B 96, 115103 (2017).
Winter, S. M. et al. Breakdown of magnons in a strongly spin-orbital coupled magnet. Nat. Commun. 8, 1152 (2017).
Sears, J. A. et al. Ferromagnetic Kitaev interaction and the origin of large magnetic anisotropy in α-RuCl3. Nat. Phys. 16, 837–840 (2020).
Johnson, R. D. et al. Monoclinic crystal structure of α-RuCl3 and the zigzag antiferromagnetic ground state. Phys. Rev. B 92, 235119 (2015).
Janssen, L., Andrade, E. C. & Vojta, M. Honeycomb-lattice Heisenberg-Kitaev model in a magnetic field: spin canting, metamagnetism, and vortex crystals. Phys. Rev. Lett. 117, 277202 (2016).
Chern, L. E., Kaneko, R., Lee, H.-Y. & Kim, Y. B. Magnetic field induced competing phases in spin-orbital entangled Kitaev magnets. Phys. Rev. Res. 2, 013014 (2020).
Holstein, T. & Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 58, 1098–1113 (1940).
Jones, D. H., Pankhurst, Q. A. & Johnson, C. E. Spin-wave theory of anisotropic antiferromagnets in applied magnetic fields. J. Phys. C: Solid State Phys. 20, 5149–5159 (1987).
Cônsoli, P. M., Janssen, L., Vojta, M. & Andrade, E. C. Heisenberg-Kitaev model in a magnetic field: 1/S expansion. Phys. Rev. B 102, 155134 (2020).
Hasegawa, Y. & Kohmoto, M. Quantum hall effect and the topological number in graphene. Phys. Rev. B 74, 155415 (2006).
Rhim, J.-W. & Park, K. Self-similar occurrence of massless dirac particles in graphene under a magnetic field. Phys. Rev. B 86, 235411 (2012).
Peierls, R. On the theory of diamagnetism of conduction electrons. Z. Phys. 80, 763–791 (1933).
Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).
Nakata, K., Klinovaja, J. & Loss, D. Magnonic quantum Hall effect and Wiedemann-Franz law. Phys. Rev. B 95, 125429 (2017).
Owerre, S. Magnonic Floquet Hofstadter butterfly. Ann. Phys. 399, 93–107 (2018).
Matsumoto, R. & Murakami, S. Theoretical prediction of a rotating magnon wave packet in ferromagnets. Phys. Rev. Lett. 106, 197202 (2011).
Matsumoto, R., Shindou, R. & Murakami, S. Thermal Hall effect of magnons in magnets with dipolar interaction. Phys. Rev. B 89, 054420 (2014).
Murakami, S. & Okamoto, A. Thermal Hall effect of magnons. J. Phys. Soc. Jpn. 86, 011010 (2017).
Shindou, R., Matsumoto, R., Murakami, S. & Ohe, J.-i Topological chiral magnonic edge mode in a magnonic crystal. Phys. Rev. B 87, 174427 (2013).
Kasahara, Y. et al. Unusual thermal Hall effect in a Kitaev spin liquid candidate α-RuCl3. Phys. Rev. Lett. 120, 217205 (2018).
Villain, J., Bidaux, R., Carton, J.-P. & Conte, R. Order as an effect of disorder. J. Phys. (Paris) 41, 1263 (1980).
Jang, S.-H., Sano, R., Kato, Y. & Motome, Y. Antiferromagnetic Kitaev interaction in f-electron based honeycomb magnets. Phys. Rev. B 99, 241106 (2019).
Winter, S. M., Riedl, K., Kaib, D., Coldea, R. & Valentí, R. Probing α-RuCl3 beyond magnetic order: effects of temperature and magnetic field. Phys. Rev. Lett. 120, 077203 (2018).
Banerjee, A. et al. Excitations in the field-induced quantum spin liquid state of α-RuCl3. NPJ Quantum Mater. 3, 8 (2018).
Balz, C. et al. Finite field regime for a quantum spin liquid in α-RuCl3. Phys. Rev. B 100, 060405 (2019).
Liu, K., Sadoune, N., Rao, N., Greitemann, J. & Pollet, L. Revealing the phase diagram of Kitaev materials by machine learning: Cooperation and competition between spin liquids. Preprint at https://arxiv.org/abs/2004.14415 (2020).
Sørensen, E. S., Catuneanu, A., Gordon, J. S. & Kee, H.-Y. Heart of entanglement: Chiral, nematic, and incommensurate phases in the Kitaev-Gamma ladder in a field. Phys. Rev. X 11, 011013 (2021).
Zhang, S.-S., Ishizuka, H., Zhang, H., Halász, G. B. & Batista, C. D. Real-space berry curvature of itinerant electron systems with spin-orbit interaction. Phys. Rev. B 101, 024420 (2020).
Berg, B. & Lüscher, M. Definition and statistical distributions of a topological number in the lattice O(3)σ-model. Nucl. Phys. B 190, 412–424 (1981).
Van Oosterom, A. & Strackee, J. The solid angle of a plane triangle. IEEE Trans. Biomed. Eng. BME-30, 125–126 (1983).
Fukui, T., Hatsugai, Y. & Suzuki, H. Chern numbers in discretized Brillouin zone: efficient method of computing (spin) Hall conductances. J. Phys. Soc. Jpn. 74, 1674–1677 (2005).
Hatsugai, Y. Explicit gauge fixing for degenerate multiplets: a generic setup for topological orders. J. Phys. Soc. Jpn. 73, 2604–2607 (2004).
Hatsugai, Y. Characterization of topological insulators: chern numbers for ground state multiplet. J. Phys. Soc. Jpn. 74, 1374–1377 (2005).
Landau, L. D. & Lifshitz, E. M. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Phys. Z. Sowjetunion 8, 153 (1935).
Lakshmanan, M. The fascinating world of the Landau-Lifshitz-Gilbert equation: an overview. Phil. Trans. R. Soc. A. 369, 1280–1300 (2011).
Rackauckas, C. & Nie, Q. DifferentialEquations.jl–a performant and feature-rich ecosystem for solving differential equations in Julia. J. Open. Res. Softw. 5, 15 (2017).
Rackauckas, C. & Nie, Q. Confederated modular differential equation APIs for accelerated algorithm development and benchmarking. Adv. Eng. Softw. 132, 1 (2019).
Acknowledgements
We thank Moon Jip Park and Hae-Young Kee for useful discussions. This work was supported by the NSERC of Canada and the Center for Quantum Materials at the University of Toronto. L.E.C. was further supported by the Ontario Graduate Scholarship. Y.B.K. was further supported by the Killam Research Fellowship from the Canada Council for the Arts. Most of the computations were performed on the Cedar and Niagara clusters, which are hosted by WestGrid and Scinet in partnership with Compute Canada.
Author information
Authors and Affiliations
Contributions
L.E.C. did the analysis at zero temperature and calculated the thermal Hall conductivity. F.L.B. performed the Monte Carlo simulations at finite temperature and calculated the static and dynamical spin structure factors. Y.B.K. conceived and supervised the study. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chern, L.E., Buessen, F.L. & Kim, Y.B. Classical magnetic vortex liquid and large thermal Hall conductivity in frustrated magnets with bond-dependent interactions. npj Quantum Mater. 6, 33 (2021). https://doi.org/10.1038/s41535-021-00331-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-021-00331-8