Abstract
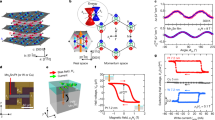
Magnetic Weyl semimetals with spontaneously broken time-reversal symmetry exhibit a large intrinsic anomalous Hall effect originating from the Berry curvature. To employ this large Hall current for room temperature topo-spintronics applications, it is necessary to fabricate these materials as thin or ultrathin films. Here, we experimentally demonstrate that Weyl semimetal Co2MnGa thin films (20–50 nm) show a large anomalous Hall angle ~11.4% at low temperature and ~9.7% at room temperature, which can be ascribed to the non-trivial topology of the band structure with large intrinsic Berry curvature. However, the anomalous Hall angle decreases significantly with thicknesses below 20 nm, which band structure calculations confirm is due to the reduction of the majority spin contribution to the Berry curvature. Our results suggest that Co2MnGa is an excellent material to realize room temperature topo-spintronics applications; however, the significant thickness dependence of the Berry curvature has important implications for thin-film device design.
Similar content being viewed by others
Introduction
In Weyl semimetals (WSMs), a type of topological semimetal, the valence and conduction bands touch each other at isolated points called Weyl nodes, which can be understood as the monopoles and anti-monopoles of Berry curvature in momentum space1. Chiral Weyl fermions, as low-energy quasiparticle excitations around these Weyl nodal points, can be pumped along surface Fermi arcs that connect the paired Weyl nodes. Due to this non-trivial topology of band structure, WSMs display a rich variety of exotic transport properties2,3, like negative magnetoresistance, and giant magnitudes of anomalous Hall effect (AHE), planar Hall effect, and anomalous Nernst effect (ANE).
Magnetic WSMs additionally have spontaneously broken time-reversal symmetry, resulting in large intrinsic AHE originating from the Berry curvature4,5,6. The intrinsic AHE current is dissipationless and fully spin-polarized and therefore has great potential for spintronics applications7. There is suggestion that magnetic WSMs could allow for the quantum anomalous Hall effect to persist at high temperatures8. Recently, kagome-lattice compound Co3Sn2S2 has been proven to be a magnetic WSM with giant anomalous Hall conductivity σxy ~1130 Ω−1 cm−1 and anomalous Hall angle, 20%9, and thin films also exhibit the same transport behaviour as the bulk single crystal10. However, Co3Sn2S2 shows a low Curie temperature Tc = 177 K, which means it cannot be used for room temperature devices. Co-based Heusler compounds, face-centered cubic metallic compounds with space-group symmetry \(Fm\bar 3m\)(225), have been predicted to be promising candidates to realize magnetic WSMs with high Curie temperature4,6. Recent attention has also focused on magnetic Heusler alloys due to the wide tunability of the Berry curvature predicted in this materials class2,11,12.
What’s more, these materials are soft ferromagnets, meaning that the spin orientation can be easily manipulated by applying a small magnetic field. Recently, bulk examples of full Heusler ferromagnet Co2MnGa with large Curie temperature Tc ≈ 700 K have been studied and shown to display giant ANE and large anomalous Hall angle, 12%, at room temperature, due to a large net Berry curvature near the Fermi energy associated with nodal lines and Weyl points10,13,14. In addition, Tung et al.15 and Manna et al.12, by calculating the Hall conductivity contribution of the majority and minority spin channels from bulk Co2MnGa, found the spin-up and spin-down Hall currents would flow in opposite directions and the large σxy results almost entirely from the majority spin channel. In this case, the anomalous Hall current would be nearly fully spin-polarized, even though Co2MnGa is not a half-metallic ferromagnet. The combination of topological electronic properties, ferromagnetism above room temperature, and strongly spin-polarized anomalous Hall current make Co2MnGa an exceptional candidate for studying the interplay of topology and magnetism and realizing room temperature topo-spintronics applications, such as magnetic field sensing16 and generating spin-transfer torque17.
To realize these applications, Co2MnGa needs to be fabricated as thin films. There are studies of thin films prepared by molecular beam epitaxy18,19,20, flash evaporation21, or magnetron sputtering22,23,24; however, almost all of this work was done before the topological characteristics of this material were realised. Hence, there has so far been very little research about the transport properties related to the topological band structure in Co2MnGa thin films. Reichlova et al. found that Co2MnGa thin films exhibit a large ANE coefficient at 300 K, −2 to −3 μV K−1, due to the non-trivial band structure24,25. However, this coefficient decreases significantly with thickness down to 10 nm and the reason still needs to be uncovered. Very recently, Markou and Wang et al. investigated thick Co2MnGa thin films, which show the same value of anomalous Hall angle as in the single crystals26,27, but they did not address the reason for the decline of anomalous Hall angle with decreasing thickness. Investigating the properties of ultrathin films is important for understanding the prospect of producing energy-efficient, high-density spintronic devices, as well as investigating the potential effects of their low dimensionality on the Berry curvature. In previous work we showed that ultrathin (>3.5 nm) films of polycrystalline Co2MnGa display perpendicular magnetic anisotropy (PMA) in trilayer MgO/Co2MnGa/Pd stacks28, which could be used to reduce the switching current in spin-transfer torque devices29.
For a comprehensive understanding of Weyl topological effects on the AHE in magnetic WSM thin films, we systematically investigated the transport properties of Co2MnGa thin films with thicknesses from 50 nm down to 5 nm. The thicker films exhibit a large anomalous Hall angle in agreement with the recent results of Markou et al., and ascribed to the intrinsic Berry curvature as found from calculations of bulk Co2MnGa. However, for films thinner than 15 nm, the anomalous Hall angle drops significantly due to the reduction of the majority spin contribution to the Berry curvature, proving that tuning the Berry curvature can be achieved in this Heusler alloy and opening possibilities for engineering topo-spintronic materials and devices.
Results
Crystal structure
For the 50-nm film, the θ–2θ scan of XRD shows the substrate MgO(002) peak and also Co2MnGa(002) and (004) peaks, as shown in Fig. 1a, indicating a good out of plane texture. Other MgO[00 l] lines are indicated by an asterisk, *. The inset is the rocking curve from the (004) peak, and the full width at half maximum (FWHM) is 0.779° suggesting a high crystal quality. Furthermore, the X-ray φ scans from −45° to 315° (Fig. 1b) display a fourfold symmetry of the Co2MnGa(220) peak and the 45° rotation of these peaks relative to the substrate (220) peaks, confirming the epitaxial relationship of MgO(001)[100]||Co2MnGa(001)[110]. We also obtained the superstructure (111) peak with in-plane XRD, which shows fourfold symmetry in the φ scan as well, as shown in the top panel of Fig. 1b. In full Heusler alloys, the XRD peaks with all odd (hkl) indexes, like (111), are known to originate in superlattice reflections in the L21 structure30. The in-plane a–b and c-axis lattice constants are 5.765 Å and 5.759 Å (c/a = 0.999), respectively, obtained from the (004) and (111) peaks. The strain \(\varepsilon = (a_{||} - a_0)/a_0\) is estimated as −0.035%, where a0 is the lattice constant of bulk single crystal Co2MnGa (5.767 Å)31 and a|| is the in-plane lattice constant of thin film (5.765 Å). Even though the diagonal \(\sqrt 2 a\)MgO of the substrate is 5.962 Å, which could induce a 3.27% lattice mismatch, the stress in our thin film is almost fully relaxed due to the post-annealing at 550 °C for 1 h. The film roughnesses measured by XRR or AFM are below 1 nm, as shown by example for the 20-nm thick film in Fig. 1c. Fitting the XRR results in a root-mean-square roughness (Rq) of 0.7 nm, with the thickness 20 nm ±2 nm. The AFM image confirms a smooth surface morphology with a Rq of 0.5 nm, as shown in the insert of Fig. 1c.
a θ–2θ scan, the inset is the rocking curve from (004) peak, and b in-plane φ scans from −45° to 315°, for 50 nm Co2MnGa thin films. c X-ray reflectivity for the 20 nm Co2MnGa thin film, the inset is the atomic force microscopy image (5 × 5 µm2) with colour contrast (dark to bright) for the height scale corresponds to 3.5 nm. The scale bar corresponds to 1 μm.
Magnetotransport properties
Magnetic hysteresis loops of a 50-nm Co2MnGa film were measured with the external magnetic field along both the in-plane and out-of-plane directions at 300 K, as shown in Fig. 2a. These show the easy axis is along the Co2MnGa[110] direction, the same as for other Heusler alloy thin films, Co2MnAl Co2MnSi32,33, and the coercive field µ0Hc and saturation magnetization Ms are 3 mT, 600 emu cm−3, respectively. Note that the crystalline direction used in this paper refers to the Co2MnGa lattice, unless indicated otherwise. When the magnetic field is along the [100] direction, though it shows a small coercive field µ0Hc = 1 mT, the saturation field is 25 mT, larger than along the [110] direction. For the [001] direction, the saturation field is 1 T (see Supplementary Fig. 1), but it still shows a small square loop, interestingly indicating there is a small out-of-plane magnetization component at zero applied field. The uniaxial anisotropy energy density calculated from the hard [001] and easy [110] directions is 3.05 × 106 erg cm−3. The Hall resistivity as a function of magnetic field was measured at 300 K and 3 K, respectively, as shown in Fig. 2b. For all of our samples, the current was applied along the [100] direction. The pure anomalous Hall resistivity was calculated by using \(\rho _{\mathrm{H}}^{\mathrm{A}} = \rho _{{\mathrm{xy}}} - R_{\mathrm{o}}B_{\mathrm{z}}\), where Ro is the ordinary Hall coefficient and Bz is the magnetic flux density along out-of-plane direction. The Hall coefficient Ro is negative and quite small, −2.42 × 10−4 cm3 C−1 (300 K) and −1.06 × 10−4 cm3 C−1 (3 K), meaning that charge carriers are of the electron type. The anomalous Hall saturation fields at 300 and 3 K are 1.3 and 1.6 T, respectively. The anomalous Hall resistivities are 17.1 and 15.4 μΩ cm at 300 and 3 K, respectively, and the ordinary Hall resistivities at 9 T are 0.218 μΩ cm (300 K) and 0.095 μΩ cm (3 K). The Hall carrier concentration and Hall mobility are 2.58 × 1022 cm−3 and 1.41 cm2 V−1 s−1, respectively, at 300 K. Since the ordinary Hall resistivity is negligible in our samples, it is safe to adopt ρxy as nearly equal to the anomalous Hall resistivity. The knot in the resistivity curve also indicates the out-of-plane magnetization component seen in the magnetization measurements. In Fig. 2c, the temperature dependence of Hall resistivity ρxy and longitudinal resistivity ρxx obtained from 300 to 3 K are plotted. The 50-nm Co2MnGa thin film has a residual resistivity ρo = 136 μΩ cm at 23 K and exhibits a typical metallic behaviour at higher temperature (red curve). The ρxyincreases with T, displaying a maximum value 17 μΩ cm around 210 K, followed by a decrease to higher temperature (blue curve). The Curie temperature of Co2MnGa is much higher than room temperature (see Supplementary Fig. 2), and consistent with the bulk Tc ~700 K34. The Hall conductivity σxy and longitudinal conductivity σxx were calculated by using \(\sigma _{{\mathrm{xy}}} = \rho _{{\mathrm{xy}}}/(\rho _{{\mathrm{xy}}}^2 + \rho _{{\mathrm{xx}}}^2(0T))\) and \(\sigma _{{\mathrm{xx}}} = \rho _{{\mathrm{xx}}}/(\rho _{{\mathrm{xy}}}^2 + \rho _{{\mathrm{xx}}}^2(0T))\), respectively. Both Hall conductivity (blue curve) and longitudinal conductivity (red curve) increase monotonically on cooling and approach constant values of 812 and 7250 Ω−1 cm−1, respectively, at low temperature, as shown in Fig. 2d.
a Magnetization measured at 300 K with the magnetic field along in-plane and out-of-plane direction, respectively. b Anomalous Hall effect measurements at 3 and 300 K, respectively. c Longitudinal resistivity without field (red) and Hall resistivity cooling down with 9 T (blue) as a function of temperature from 3 to 300 K. d the corresponding conductivity as a function of temperature from 3 to 300 K.
The anomalous Hall angle can be calculated by using \(\theta _{\mathrm{H}} = \sigma _{{\mathrm{xy}}}/\sigma _{{\mathrm{xx}}}\). Figure 3a shows the anomalous Hall angle as a function of temperature from 300 to 3 K. The 50-nm topological semimetal Co2MnGa thin film shows a large anomalous Hall angle θH = 9.7% at 300 K, increasing at low temperature to reach a maximum value 11.4% at 113 K. Usually, typical ferromagnetic thin films with topologically trivial band structure show a small angle, less than 3%35. Even though some non-magnetic Weyl semimetals exhibit giant anomalous Hall angle in single crystals36,37, to date only Co2MnGa shows such a large anomalous Hall angle in thin films at room temperature.
a Temperature dependent anomalous Hall angle measured from 3 to 300 K for 50 nm Co2MnGa. b Thickness dependence of anomalous Hall angle as a function of temperature from 3 to 300 K, the inset is the maximum anomalous Hall angle as a function of thickness. c Log \(\sigma _{{\mathrm{xy}}}\) - \(\sigma _{{\mathrm{xx}}}\) plot for Co2MnGa with thicknesses from 5 to 50 nm. d, e Thickness dependence of \(\sigma _{{\mathrm{xx}}}\) and \(\sigma _{{\mathrm{xy}}}\) as a function of temperature from 3 to 300 K, respectively.
In non-magnetic WSMs, the existence of planar Hall effects or negative magnetoresistances has also been taken as further evidence of the effect of the Weyl character of the band structure on the electronic transport38,39. However, both of these effects are present in magnetic non-Weyl materials also, and the measurements of these effects in magnetic WSM Co3Sn2S2 are unremarkable and consistent with a trivial magnetic origin40. In Supplementary Figs. 4 and 5 we show the angle-dependent planar Hall effect and magnetoresistance of our films measured along several crystallographic directions. The magnitudes of these effects are similar to those measured in Co3Sn2S29,40 and are not larger than in typical magnetic non-Weyl materials. What’s more, the linear negative MR observed at high field in Co2MnGa when the magnetic field is parallel to the current, as shown in Supplementary Fig. 5, can be ascribed to the thermal-induced spin disorder, which is a typical ferromagnet behaviour41,42. Therefore, we consider the large anomalous Hall angle to be the only consistent magnetotransport indicator of the topological non-trivial band structure in ferromagnetic WSMs such as Co2MnGa.
To understand the thickness dependence of the anomalous Hall angle, we fabricated Co2MnGa films with smaller thicknesses, from 20 to 5 nm. Supplementary Fig. 3 shows the ρxx and ρxy as a function of temperature from 3 to 300 K for Co2MnGa (5–50 nm). Figure 3b shows the thickness dependence of the anomalous Hall angle measured from 300 to 3 K. Once we decrease the thickness to 20 nm, the anomalous Hall angle is still large, around 11%, and this film shows a similar trend as the 50-nm film when decreasing the temperature. However, for samples with thicknesses of 15, 10, and 5 nm, the anomalous Hall angle is temperature independent, and the value drops to 3.3%, 2.7%, and 1.3%, respectively. The inset shows the maximum value of each sample, as measured between 3 and 300 K. Our results of thinner samples agree very well with ref. 42 in which the anomalous Hall angle of 6 nm Co2MnGa is no more than ~2.8%. Figure 3c is the log σxy - \(\sigma _{{\mathrm{xx}}}\) plot for all samples measured at 300 to 3 K. \(\sigma _{{\mathrm{xx}}}\) is about 4.5–7.5\(\times\)103 Ω−1 cm−1 at various thicknesses and temperatures, and σxy is nearly independent of \(\sigma _{{\mathrm{xx}}}\). For the samples with thicknesses from 50 to 20 nm, one can see that σxy is nearly constant (around 700 Ω−1 cm−1). It is known that there exist three regimes in the scaling behaviour of the AHE depending on the range of \(\sigma _{{\mathrm{xx}}}\), categorized by a scaling parameter, \(\alpha\), in \(\sigma _{{\mathrm{xy}}} \propto \sigma _{{\mathrm{xx}}}^\alpha\)43. The values of \(\sigma _{{\mathrm{xx}}}\) of all samples are close to the intermediate region as defined in ref. 43, where \(\sigma _{{\mathrm{xx}}}\) = 104–106 Ω−1 cm−1. Furthermore, this constant value of σxy is close to the order of the intrinsic contribution. This is the value expected from the intrinsic scattering-independent mechanism originating from the Berry curvature in momentum space, and indicates that σxy in our films is dominated by the intrinsic component due to the non-trivial topology of band structure of Co2MnGa35. However, for the thinner samples with thicknesses of 15, 10, and 5 nm, the values of σxy drop steeply to 170, 160, and 70 Ω−1 cm−1, respectively. Since the values of σxy of these samples are much smaller than the order of the intrinsic contribution, the σxy might be due not only to the intrinsic scattering, but also might include contributions from the extrinsic side-jump mechanism, which can also induce values of σxy that are independent of σxy44. This agrees with our previous results that the σxy of polycrystalline MgO/Co2MnGa/Pd ultrathin films results from both intrinsic and side-jump scattering28. Figure 3d and e show the \(\sigma _{{\mathrm{xx}}}\) and \(\sigma _{{\mathrm{xy}}}\) against the temperature and thickness, respectively. The \(\sigma _{{\mathrm{xx}}}\) slightly increases with decreasing temperature, and then remains constant at low temperature. \(\sigma _{{\mathrm{xx}}}\) for all samples at various temperatures varies only by ~25%; however, the σxy drops suddenly once the thickness is below 15 nm. For instance, comparing the 50 nm and 10 nm films, the \(\sigma _{{\mathrm{xx}}}\) of both is around 7.2 × 103 Ω−1 cm−1 at 3 K, but the σxy drops from 810 to 160 Ω−1 cm−1 for the thinner film.
Evolution of Berry curvature and surface band structure
The intrinsic contribution to the σxy is dependent only on the band structure of a material. It can be calculated from the Kubo formula for the Hall conductivity
where \(f(\varepsilon _k)\) is the Fermi-Dirac distribution function, Ωz is the z-component Berry curvature45. The \(\sigma _{{\mathrm{xy}}}\) can also be found from the sum of the conductivities for majority spin electrons (↑) and minority spin electrons (↓), \(\sigma _{{\mathrm{xy}}} = \sigma _{{\mathrm{xy}}}^ \uparrow + \sigma _{{\mathrm{xy}}}^ \downarrow\). Thus, the spin polarization-dependent conductivities \(\sigma _{{\mathrm{xy}}}^ \uparrow\) and \(\sigma _{{\mathrm{xy}}}^ \downarrow\) can be calculated by taking the integral of \({\mathrm{{\Omega}}}_{\mathrm{z}}^ \uparrow\) and \({\mathrm{{\Omega}}}_{\mathrm{z}}^ \downarrow\) over the entire Brillouin zone (BZ). Manna et al., by calculating the Hall conductivity contribution of the majority and minority spin channels from bulk Co2MnGa, found \(\sigma _{{\mathrm{xy}}}\) ~1600 Ω−1 cm−1 and \(\sigma _{{\mathrm{xy}}}^ \downarrow\) is almost equal to 0 at the Fermi level (EF)12. The value of \(\sigma _{{\mathrm{xy}}}\) in our thin films is half that of bulk Co2MnGa. However, interestingly we have almost the same anomalous Hall angle of the bulk reports, 12%, since the value of \(\sigma _{{\mathrm{xx}}}\) in our thin film is relatively smaller than in ref. 12.
To understand the influence of spin-dependent electrons for \(\sigma _{{\mathrm{xy}}}\) of Co2MnGa thin films with different thickness, we calculate the averaged z-component of the Berry curvature (total Berry curvature/number of slabs) and surface band structure from majority spin electrons and minority spin electrons near the Fermi level in the kx − ky plane, respectively, as shown in Fig. 4 and Supplementary Fig. 6. For 123 primitive cell (50.1 nm) thick slab of Co2MnGa, \({\mathrm{{\Omega}}}_{\mathrm{z}}^ \uparrow \gg {\mathrm{{\Omega}}}_{\mathrm{z}}^ \downarrow\) (see Fig. 4b, d), meaning \(\sigma _{{\mathrm{xy}}}^ \uparrow \gg \sigma _{{\mathrm{xy}}}^ \downarrow\) and suggesting that the Berry curvature contribution to \(\sigma _{{\mathrm{xy}}}\) from the majority spin electrons is much higher than that from minority spin electrons, which is the same as for bulk Co2MnGa. Recent work has confirmed this by spin-resolved angle-resolved photoelectron spectroscopy on a 50-nm Co2MnGa thin film46. The magnitude of \({\mathrm{{\Omega}}}_{\mathrm{z}}^ \uparrow\) of this thick Co2MnGa film is close to bulk values and is consistent with the \(\sigma _{{\mathrm{xy}}}\) values calculated by others10,12,15, suggesting films of ~50-nm thickness still show the bulk-like properties, like the large \(\sigma _{{\mathrm{xy}}}\) originating from the non-trivial topology of the band structure with large intrinsic Berry curvature. The \({\mathrm{{\Omega}}}_{\mathrm{z}}^ \uparrow\) for the 50-nm film in Fig. 4 is complicated because it includes multiple ‘slabs’ in the calculation, and at 50 nm there is not yet enough overlap of the states so that continuous bulk-like bands are formed. Once we decrease the thickness to 4.9 nm (12 primitive cells), \({\mathrm{{\Omega}}}_{\mathrm{z}}^ \uparrow\) drops significantly (see Fig. 4b, d). This agrees with the experimental observation that the \(\sigma _{{\mathrm{xy}}}\) reduces when film thickness decreases. Figure 4e and f summarises the \({\mathrm{{\Omega}}}_{\mathrm{z}}^ \uparrow\) and \({\mathrm{{\Omega}}}_{\mathrm{z}}^ \downarrow\) as a function of k along the Г-М line for various thicknesses. The extent of Berry curvature reduction for majority spins is more significant than that for minority spins. Once the thickness is down to 20 nm, the \({\mathrm{{\Omega}}}_{\mathrm{z}}^ \uparrow\) slightly drops, but it is still close to the bulk value indicating that the \(\sigma _{{\mathrm{xy}}}\) is robust down to this thickness. Below 15 nm, the role of the surface becomes more important, which could result in extrinsic side-jump scattering and might suppress the effect of the Weyl nodes on the magnetotransport. What’s more, there is a 3.27% lattice mismatch between Co2MnGa and the MgO substrate. Though the stress in the 50-nm film is almost fully relaxed due to the post-annealing, there could be a tetragonal distortion at low thickness which might induce an energy shift of the Weyl nodes47 or shift the electron density-of-states48. Note the very different maxima used in the scales of Fig. 4a–d vs Fig. 4e–f, so that the main features can be seen in Fig. 4a–d, and the very large spikes can be seen in Fig. 4e–f.
a–d show the calculated averaged-integral of z-component Berry curvature (\({\mathrm{{\Omega}}}_{\mathrm{z}}\)) of occupied bands from minority and majority spin electrons for Co2MnGa thin films of 4.9 nm and 50.1 nm, e, f show a comparison of \({\mathrm{{\Omega}}}_{\mathrm{z}}\) along Γ-M line for Co2MnGa thin films of 4.9, 15.0, 20.0, and 50.1 nm.
Discussion
By comparing to previously reported results of thin films, including Heusler alloys and classic ferromagnetic transition metal and alloys, the anomalous Hall angle in Co2MnGa shows a large value, 11.4%, and also a comparatively large Hall conductivity 775 Ω−1 cm−1, as shown in Fig. 5. To obtain a large anomalous Hall angle, the \(\sigma _{{\mathrm{xy}}}\) needs to be large, or \(\sigma _{{\mathrm{xx}}}\) needs to be small, but large \(\sigma _{{\mathrm{xy}}}\) signal with very good signal-to-noise ratio is necessary for logic or memory hybrid CMOS/AHE devices49 and AHE sensors50. Near the dirty regime45 with a small \(\sigma _{{\mathrm{xx}}}\), however, \(\sigma _{{\mathrm{xy}}}\) is suppressed more drastically than \(\sigma _{{\mathrm{xx}}}\), due to quasiparticle damping or spoiling of the resonance condition51. For ferromagnetic systems, both \(\sigma _{{\mathrm{xy}}}\) and \(\sigma _{{\mathrm{xy}}}\) are either large or small, and therefore the anomalous Hall angle is usually not very large. Though Co3Sn2S2 thin films have a giant anomalous Hall angle 20%, it shows a low Curie temperature Tc = 177 K as we mentioned before. Even for exceptions such as the compensated Heusler ferrimagnet Mn2-xRuxGa, which has a large anomalous Hall angle 7.7% at 300 K, it displays a small \(\sigma _{{\mathrm{xy}}}\), around 220 Ω−1 cm−1 52.
The reported results were taken or calculated from references (see Supplementary Table 1).
In summary, we have prepared high quality epitaxial films of the topological semimetal Co2MnGa with thicknesses from 5 to 50 nm on MgO substrates and established they have a similar large anomalous Hall angle at room temperature as in bulk crystals. For the 50-nm thick film, it shows large \(\sigma _{{\mathrm{xy}}}\) ~775 Ω−1 cm−1 and anomalous Hall angle 11.4% at 113 K. The origin of the large \(\sigma _{{\mathrm{xy}}}\) is the large net Berry curvature near the EF due to the non-trivial topology of band structure of Co2MnGa, and still shows a large anomalous Hall angle 9.7% at 300 K. The bulk-like properties are robust, for film thicknesses down to 20 nm. Once we decrease thickness below 20 nm, the \(\sigma _{{\mathrm{xy}}}\) suddenly drops a lot with a slight change of \(\sigma _{{\mathrm{xx}}}\), with a corresponding decrease in the anomalous Hall angle. From our band structure calculations, we ascribe the decrease to the reduction of the majority spin electron Berry curvature. Our results confirm that Co2MnGa is a topological magnetic material in which tuning of the Berry curvature is possible, as observed in the anomalous Hall behaviour. The opportunity to control the Berry curvature in materials provides a way to realize topo-spintronic logic or memory devices and AHE sensors that operate at room temperature.
Methods
Sample preparation
Co2MnGa (5–50 nm) thin films were epitaxially deposited on single-crystalline MgO(001) substrates in a Kurt J Lesker CMS-18 magnetron sputtering system with a base pressure below 5 × 10−8 Torr. Before fabricating thin films, substrates were cleaned with an Ar plasma, and then annealed at 400 °C for 1 h in the vacuum chamber. Co2MnGa thin films were DC magnetron sputtered from a stoichiometric polycrystalline target at 100 W under 6 mTorr of Ar with a growth rate of 0.8 Å s−1 at 400 °C while rotating the sample holder. All samples were post-annealed in situ at 550 °C for 1 h to improve the lattice structure and the atomic ordering among Co, Mn, and Ga sites. After cooling down to ambient temperature, a 2-nm protective MgO layer was deposited on the top. Samples were patterned into standard Hall bars (l = 2000 µm, w = 150 µm) by photolithography and then Ar ion milling for magnetotransport characterization.
Thin-film characterization
The crystalline structure of the Co2MnGa thin films was characterized by X-ray diffraction (XRD) with Co Kα radiation (λ = 1.7889 Å) using a Bruker D8 Advance. The film thicknesses were checked by X-ray reflectivity (XRR) using a PANalytical X’Pert PRO. Atomic force microscopy (AFM) was carried out on a Nanosurf FlexAFM mounted on a Nanosurf Isostage active vibration cancellation stand.
Magnetization and electric transport measurements
Magnetization measurements were performed using the RSO module of a Superconducting Quantum Interference Device magnetometer (SQUID, Quantum Design). The transport measurements were performed using the resistivity option of a Physical Property Measurement System (PPMS, Quantum Design).
Band structure calculation method
We used density functional theory (DFT) calculations as implemented in the Vienna ab initio Simulation Package (VASP) to calculate the optimized geometry and the electronic structure of Co2MnGa53. The Perdew-Burke-Ernzehof (PBE) form of the generalized gradient approximation (GGA) was used to describe electron exchange and correlation54. The kinetic energy cut-off for the plane-wave basis was set to 400 eV. We used a 12 × 12 × 12 Γ-centered k-point mesh for sampling the Brillouin zone. For calculation of Berry curvature of Co2MnGa thin films, we adopted the method as implemented in the open-source code WannierTools55,56, based on the Wannier tight-binding Hamiltonian obtained from wannier9057. Co/Mn d and Ga s, p orbitals are projectors for tight-binding Hamiltonian construction.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Manna, K., Sun, Y., Muechler, L., Kübler, J. & Felser, C. Heusler, Weyl and Berry. Nat. Rev. Mater. 3, 244–256 (2018).
Hu, J., Xu, S.-Y., Ni, N. & Mao, Z. Transport of topological semimetals. Annu. Rev. Mater. Res. 49, 207–252 (2019).
Wang, Z. et al. Time-reversal-breaking Weyl fermions in magnetic Heusler alloys. Phys. Rev. Lett. 117, 236401 (2016).
Chang, G. et al. Topological Hopf and Chain link semimetal states and their application to Co2MnGa. Phys. Rev. Lett. 119, 156401 (2017).
Kübler, J. & Felser, C. Weyl points in the ferromagnetic Heusler compound Co2MnAl. Europhys. Lett. 114, 47005 (2016).
Lee, W.-L., Watauchi, S., Miller, V. L., Cava, R. J. & Ong, N. P. Dissipationless anomalous Hall current in the ferromagnetic spinel CuCr2Se4-xBrx. Science 303, 1647–1649 (2004).
Muechler, L. et al. Emerging chiral edge states from the confinement of a magnetic Weyl semimetal in Co3Sn2S2. Phys. Rev. B 101, 115106 (2020).
Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125–1131 (2018).
Belopolski, I. et al. Discovery of topological Weyl fermion lines and drumhead surface states in a room temperature magnet. Science 365, 1278–1281 (2019).
Noky, J., Zhang, Y., Gooth, J., Felser, C. & Sun, Y. Giant anomalous Hall and Nernst effect in magnetic cubic Heusler compounds. npj Comput. Mater. 6, 1–8 (2020).
Manna, K. et al. From Colossal to Zero: controlling the anomalous Hall effect in magnetic Heusler compounds via Berry curvature design. Phys. Rev. X 8, 041045 (2018).
Guin, S. N. et al. Anomalous Nernst effect beyond the magnetization scaling relation in the ferromagnetic Heusler compound Co2MnGa. NPG Asia Mater. 11, 1–9 (2019).
Sakai, A. et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal. Nat. Phys. 14, 1119–1124 (2018).
Tung, J.-C. & Guo, G.-Y. High spin polarization of the anomalous Hall current in Co-based Heusler compounds. N. J. Phys. 15, 033014 (2013).
Lu, Y. M., Cai, J. W., Pan, H. Y. & Sun, L. Ultrasensitive anomalous Hall effect in SiO2/Fe-Pt/SiO2 sandwich structure films. Appl. Phys. Lett. 100, 022404 (2012).
Iihama, S. et al. Spin-transfer torque induced by the spin anomalous Hall effect. Nat. Electron. 1, 120–123 (2018).
Holmes, S. N. & Pepper, M. Magnetic and electrical properties of Co2MnGa grown on GaAs (001). Appl. Phys. Lett. 81, 1651–1653 (2002).
Yu, C., Pechan, M. J., Carr, D. & Palmstrøm, C. J. Ferromagnetic resonance in the stripe domain state: a study in Co2MnGa (001). J. Appl. Phys. 99, 08J109 (2006).
Hassan, S. S. A. et al. The properties and structure relationship of half metallic magnetic materials on GaAs. IEEE Trans. Magn. 45, 4360–4363 (2009).
Kudryavtsev, Y. V. et al. Evolution of the magnetic properties of Co2MnGa Heusler alloy films: From amorphous to ordered films. Phys. Rev. B 76, 024430 (2007).
Kolbe, M. et al. Test of band structure calculations for Heusler compounds by spin-resolved photoemission spectroscopy. Phys. Rev. B 86, 024422 (2012).
Sato, T. et al. Large negative anisotropic magnetoresistance in Co2MnGa Heusler alloy epitaxial thin films. Appl. Phys. Lett. 113, 112407 (2018).
Reichlova, H. et al. Large anomalous Nernst effect in thin films of the Weyl semimetal Co2MnGa. Appl. Phys. Lett. 113, 212405 (2018).
Park, G.-H. et al. Thickness dependence of the anomalous Nernst effect and the Mott relation of Weyl semimetal Co2MnGa thin films. Phys. Rev. B 101, 060406 (2020).
Markou, A. et al. Thickness dependence of the anomalous Hall effect in thin films of the topological semimetal Co2MnGa. Phys. Rev. B 100, 054422 (2019).
Wang, Q., Wen, Z., Kubota, T., Seki, T. & Takanashi, K. Structural-order dependence of anomalous Hall effect in Co2MnGa topological semimetal thin films. Appl. Phys. Lett. 115, 252401 (2019).
Ludbrook, B. M., Ruck, B. J. & Granville, S. Perpendicular magnetic anisotropy in Co2MnGa and its anomalous Hall effect. Appl. Phys. Lett. 110, 062408 (2017).
Mangin, S. et al. Current-induced magnetization reversal in nanopillars with perpendicular anisotropy. Nat. Mater. 5, 210–215 (2006).
Sakuraba, Y. et al. Huge spin-polarization of L21-ordered Co2MnSi epitaxial heusler alloy film. Jpn. J. Appl. Phys. 44, L1100 (2005).
Kübler, J. Theory of Itinerant Electron Magnetism (Oxford Univ. Press, 2017).
Zhu, L. J. & Zhao, J. H. Anomalous resistivity upturn in epitaxial L21-Co2MnAl films. Sci. Rep. 7, 42931 (2017).
Liu, Y. et al. Optically induced magnetization dynamics and variation of damping parameter in epitaxial Co2MnSi Heusler alloy films. Phys. Rev. B 81, 094402 (2010).
Webster, P. J. Magnetic and chemical order in Heusler alloys containing cobalt and manganese. J. Phys. Chem. Solids 32, 1221–1231 (1971).
Miyasato, T. et al. Crossover behaviour of the anomalous Hall effect and anomalous Nernst effect in Itinerant Ferromagnets. Phys. Rev. Lett. 99, 086602 (2007).
Suzuki, T. et al. Large anomalous Hall effect in a half-Heusler antiferromagnet. Nat. Phys. 12, 1119–1123 (2016).
Singha, R., Roy, S., Pariari, A., Satpati, B. & Mandal, P. Magnetotransport properties and giant anomalous Hall angle in the half-Heusler compound TbPtBi. Phys. Rev. B 99, 035110 (2019).
Hirschberger, M. et al. The chiral anomaly and thermopower of Weyl fermions in the half-Heusler GdPtBi. Nat. Mater. 15, 1161–1165 (2016).
Xiong, J. et al. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 350, 413–416 (2015).
Shama, Gopal,R. K. & Singh, Y. Observation of planar Hall effect in the ferromagnetic Weyl semimetal Co3Sn2S2. J. Magn. Magn. Mater. 502, 166547 (2020).
Chen, Y.-C. et al. Heteroepitaxy of Co-based Heusler compound/muscovite for flexible spintronics. ACS Appl. Mater. Interfaces 11, 35162–35168 (2019).
Tong, S., Zhao, X., Wei, D. & Zhao, J. Low-temperature resistivity anomaly and weak spin disorder in Co2MnGa epitaxial thin films. Phys. Rev. B 101, 184434 (2020).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Onoda, S., Sugimoto, N. & Nagaosa, N. Intrinsic versus extrinsic anomalous Hall effect in ferromagnets. Phys. Rev. Lett. 97, 126602 (2006).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Sumida, K. et al. Spin-polarized Weyl cones and giant anomalous Nernst effect in ferromagnetic Heusler films. Commun. Mater. 1, 89 (2020).
Schindler, C. et al. Effect of uniaxial stress on the electronic band structure of NbP. Phys. Rev. B 102, 035132 (2020).
Ayuela, A., Enkovaara, J., Ullakko, K. & Nieminen, R. M. Structural properties of magnetic Heusler alloys. J. Phys. Condens. Matter 11, 2017–2026 (1999).
Moritz, J., Rodmacq, B., Auffret, S. & Dieny, B. Extraordinary Hall effect in thin magnetic films and its potential for sensors, memories and magnetic logic applications. J. Phys. D Appl. Phys. 41, 135001 (2008).
Vilanova Vidal, E., Stryganyuk, G., Schneider, H., Felser, C. & Jakob, G. Exploring Co2MnAl Heusler compound for anomalous Hall effect sensors. Appl. Phys. Lett. 99, 132509 (2011).
Kim, K. et al. Large anomalous Hall current induced by topological nodal lines in a ferromagnetic van der Waals semimetal. Nat. Mater. 17, 794–799 (2018).
Thiyagarajah, N. et al. Giant spontaneous Hall effect in zero-moment Mn2RuxGa. Appl. Phys. Lett. 106, 122402 (2015).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Wu, Q., Zhang, S., Song, H.-F., Troyer, M. & Soluyanov, A. A. WannierTools: an open-source software package for novel topological materials. Comput. Phys. Commun. 224, 405–416 (2018).
Wang, X., Yates, J. R., Souza, I. & Vanderbilt, D. Ab initio calculation of the anomalous Hall conductivity by Wannier interpolation. Phys. Rev. B 74, 195118 (2006).
Mostofi, A. A. et al. wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Acknowledgements
We are grateful to Jérôme Leveneur from GNS science for the AFM measurements and Sarah Spencer from the Robinson Research Institute for EDX. Y.F.Y. and N.M. acknowledge the support from Australian National Computing Infrastructure and Pawsey Supercomputing Centre. The MacDiarmid Institute is supported under the New Zealand Centres of Research Excellence Programme. Y.F.Y. and N.M. are thankful for the funding support from the Australian Research Council (CE170100039).
Author information
Authors and Affiliations
Contributions
Y.Z. fabricated and characterized devices with assistance from G.D. and T.B. Y.Z. and S.G. analyzed the data. Y.F.Y. did the theoretical calculations with contributions from N.M. Y.Z. and S.G. wrote the manuscript with contributions from all authors. All authors discussed the results and commented on the manuscript. The study was performed under the supervision of S.G.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, Y., Yin, Y., Dubuis, G. et al. Berry curvature origin of the thickness-dependent anomalous Hall effect in a ferromagnetic Weyl semimetal. npj Quantum Mater. 6, 17 (2021). https://doi.org/10.1038/s41535-021-00315-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-021-00315-8
This article is cited by
-
Topologically influenced terahertz emission in Co2MnGa with a large anomalous Hall effect
NPG Asia Materials (2024)
-
Anisotropic resistance with a 90° twist in a ferromagnetic Weyl semimetal, Co2MnGa
Nature Communications (2023)
-
Bulk-Surface Electron Coupling in Weyl Semimetals
Journal of Electronic Materials (2022)