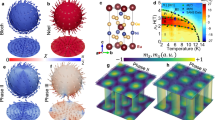
Abstract
We report a magnetic state in GaV4Se8 which emerges exclusively in samples with mesoscale polar domains and not in polar mono-domain crystals. It is manifested by a sharp anomaly in the magnetic susceptibility and the magnetic torque, distinct from other anomalies observed also in polar mono-domain samples upon transitions between the cycloidal, the Néel-type skyrmion lattice and the ferromagnetic states. We ascribe this additional transition to the transformation of distinct magnetic textures, confined to polar domain walls (DW), to the ferromagnetic (FM) state. The emergence of these DW-confined magnetic states is likely driven by the mismatch of different spin spirals, hosted by the adjacent domains. A clear anomaly in the magneto-current indicates that the DW-confined magnetic states also have strong contributions to the magnetoelectric response. We expect polar DWs to commonly host such confined magnetic edge states and, thus, offer a fertile ground to explore novel forms of magnetism.
Similar content being viewed by others
Introduction
Geometrical or dimensional constraints can promote the formation of new quantum phases which are absent in bulk systems. Prominent examples include metallic surface states in topological insulators1, superconducting vortex state below the Kosterlitz–Thouless transition2, interface-induced 2D electron gas3 and superconductivity4,5,6, integer and fractional quantum Hall edge states7,8,9 and Wigner crystals10,11 in systems with reduced dimensions. Geometrical constraints on the nano- to mesoscale are usually enforced by design in quantum dots, nanowires, thin films, heterostructures, metamaterials, etc. Such constraints can also be imposed naturally via mesoscale domain patterns or topological defects on the atomic scale12,13,14,15,16,17,18,19.
Indeed, domain walls (DW) in ferroelectrics have recently been reported to possess novel functionalities, such as unusual DW conductivity, electrical rectification and super switching, as observed in YMnO313,20, ErMnO321, BiFeO316,22, LiNbO323, PbxSr1−xTiO324, etc. Besides the peculiar electrical properties of DWs, the atomically sharp structural changes associated with them can substantially modify the magnetic exchange interactions and spin ordering, as reported for SrRuO3–Ca0.5Sr0.5TiO3 heterostructures and thin films of La2/3Sr1/3MnO3 and TbMnO319,25,26. Furthermore, geometrical confinement were shown to substantially increase the thermal stability range of magnetic skyrmions27,28,29, which are whirling spin textures on the nanoscale, and were proposed to generate exotic magnetic edge states, such as chiral bobbers30.
Lacunar spinels with the chemical formula AB4X8 (A = Al, Ga, Ge; B = V, Mo, Nb, Ta; X = S, Se, Te) are a family of narrow-gap Mott insulators31,32, exhibiting a plethora of correlation and spin-orbit effects, including pressure-induced superconductivity33, bandwidth-controlled metal-to-insulator transition34, electric-field-driven avalanche of the Mott gap35, large negative magnetoresistance36, two-dimensional topological insulator state37 and orbitally driven ferroelectricity38,39,40,41. In addition to these charge related phenomena and particularly important for the present study, lacunar spinels, such as GaV4S8, GaV4Se8 and GaMo4S8, were the first material family found to host the Néel-type skyrmion lattice (SkL) state42,43,44. In the last two compounds, the SkL state was reported to be stable even in their ground state. While these materials have a cubic structure (\(F\overline{4}3m\)) at high temperature, many of them transform to a rhombohedral state (R3m) upon a Jahn–Teller transition, occuring around 30–50 K, which is triggered by the degeneracy of the B4X4 cluster orbitals39,45,46. The polar axial symmetry of the low-temperature state is a prerequisite for the emergence of the Néel-type SkL state47.
In this work, we demonstrate that in addition to the twisted spin textures existing in the bulk, a novel magnetic state, confined to polar DWs, emerge in GaV4Se8 likely due to the constraint to match distinct spin cycloids hosted by the adjacent domains.
Results
Imaging and control of polar domains
In these compounds, four polar domain states with polarizations along the cubic 〈111〉-type axes can exist. The different types of domains, with a typical width of 10–1000 nm, naturally form lamellar patterns with {100}-type neutral DWs, as observed in GaV4S818 and GaMo4S848.
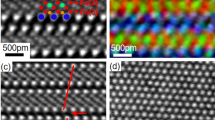
To characterize the polar domains and to estimate the density of DWs in GaV4Se8, we combined several complementary scanning probe microscopy techniques, including non-contact atomic force microscopy (nc-AFM), scanning dissipation microscopy (SDM), and frequency-modulated Kelvin-probe force microscopy (KPFM). We found that the polar multi-domain state in GaV4Se8 is also made up of mechanically and electrically compatible lamellar domains. For an overview of the corresponding results see Supplementary Fig. 1. In attempt to observe spin cycloidal and Néel-type skyrmion textures within polar domains of GaV4Se8, only evidenced by small-angle neutron scattering measurements so far43, we also carried out magnetic force microscopy (MFM) measurements. A second purpose of the MFM study was to explore possible magnetic states confined to the vicinity of DWs, as reported in GaV4S818,42.
Figure 1a, b shows MFM images respectively recorded on as-grown (111) and (001) surfaces of GaV4Se8 crystals below the magnetic ordering temperature. Though MFM was specifically applied to detect magnetic textures in polar domains as well as at DWs, no magnetic structures were observed in subsequent trials on as-grown and cleaved surfaces. Instead, we found lamellar domain patterns, similar to those observed with the other scanning probe methods mentioned above. The domains and the DWs appear in the frequency shift signal as bright stripes and dark lines, respectively. Their contrast is not affected by magnetic field, reflecting its non-magnetic origin. The typical domain width varies in the range of 100–500 nm.
a, b Frequency shift image obtained at 8.4 K on a (111) surface and at 11 K on a (001) surface, respectively. The color represents the shift in the cantilever resonance frequency, given in [Hz] units in the color bar. The contrast is not due to magnetic textures but reflects the polar domain pattern.
Besides the high DW density, another peculiarity of this polar phase is the lack of 180° DWs and the presence of 109° DWs only, a consequence of the non-centrosymmetric cubic phase18,48. (This is in contrast to perovskite ferroelectrics, where the paraelectric cubic phase is centrosymmetric.) In the lack of ±P domains, electric fields of opposite signs, applied along one of the four 〈111〉-type axes, select either the unique domain with polarization parallel to the field or the other three domains, whose polarizations span 71° with the electric field. Such control of the polar domains is sketched in Fig. 2 and also demonstrated via the temperature-dependent polarization, which was determined from pyrocurrent measurements, following electric-field poling. Indeed, the maximum polarization reached via positive poling fields (2.0 μC cm−2) is considerably larger than for negative fields (−0.45 μC cm−2). The ratio of the polarization values in the P1 mono-domain and multi-domain states involving the other domains is expected to be 3:1 in the previous scenario, since the pyrocurrent component along the P1 polar axis was detected.
a Temperature dependence of the polarization along the [111] axis, measured during heating after poling with different electric fields, Ep∥[111], upon cooling. The dashed line indicates the saturation polarization expected for negative poling fields. b, c Schematic representations of the cubic unit cell indicating the four possible directions of the polarization, P1−4, emerging in the rhombohedral phase. For +Ep, the P1 domain state is favored (b), for −Ep, the P2−4 domain states are favored (c). In the magneto-current and torque experiments, described later, the magnetic field was rotated in the (1\(\overline{1}\)0) plane, highlighted in orange in b. The angle ϕ is spanned by the field and the [111] axis.
Magnetic states in mono- and multi-domain crystals
The different types of polar domains are also distinguished magnetically, since they are characterized by different directions of uniaxial anisotropy, coinciding with their polar axes43,49,50, and by different orientations of the Dzyaloshinskii–Moriya vectors that prefer modulated magnetic structures with q-vectors perpendicular to their polar axes. Correspondingly, for arbitrary directions of the magnetic field, distinct magnetic states can coexist on different types of polar domains, as observed in GaV4S842.
In GaV4Se8, such sensitivity of the magnetic state to the orientation of the field was followed at 12 K by small-angle neutron scattering (SANS). A sequence of three different phases, SkL → cycloidal → ferromagnetic (FM), was observed while rotating a constant magnetic field of μ0H = 220 mT in the (1\(\overline{1}\)0) plane from the polar [111] axis (H∥) towards the perpendicular plane (H⊥), as demonstrated in Fig. 3. The SANS patterns were recorded on the (111) plane for several angles of the field.
a–d SANS images recorded at 12 K in 220 mT with the magnetic field spanning 0°, 21°, 27° and 35° with the [111] axis, respectively. The hexagonal and the ±q patterns in a and c correspond to the SkL and cycloidal (conical) states, respectively. b, d Images taken near the SkL → cycloidal and cycloidal → FM transitions, respectively.
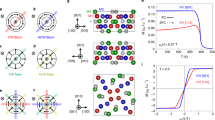
In order to continuously follow the phase boundaries on the H∥–H⊥ plane, we carried out magneto-current and magnetic torque measurements, when the magnetic field was rotated in fine steps within the (\(1\overline{1}\)0) plane between successive field sweeps. The corresponding data are depicted in Fig. 4 in the form of color maps over the field magnitude–orientation plane (ϕ denotes the angle of the field spanned with the [111] axis, as sketched in Fig. 2b), where the magnitude of the magneto-current (Fig. 4a, c) and the dissipative part of the torque signal (Fig. 4b) are represented by colors. The anomalies labeled in Fig. 4 are used to establish the magnetic phase diagrams corresponding to polar mono- and multi-domain states in Fig. 5a, b, respectively, also supplemented with magnetization, susceptibility and SANS measurements. The phase boundaries determined from torque data slightly deviate from those deduced by other methods, which is attributed to differences in the measurements conditions (precise sample temperature, direction of the field sweep, etc.). For a better match, the phase boundaries determined from torque measurements were plotted in Fig. 5a with H values rescaled by a factor of ~1.12.
Color maps of a and c, the magneto-current density and b, the dissipative part of the torque (Γ), as functions of the angle (ϕ) and the magnitude (H) of the magnetic field. Data shown in a were recorded on sample #1 poled into a nearly P1 mono-domain state, while data shown in c were obtained on sample #2 realizing a multi-domain state with comparable population of the different types of domains. Torque was also measured on a polar multi-domain crystal. d A magnified view of the frame indicated (c), as a waterfall diagram, where the magneto-current curves recorded at different angles are shifted horizontally in proportion to ϕ. For clarity, strong features in the top right and top left corners are not displayed. In each panel, the anomalies assigned to magnetic phase boundaries are indicated by solid or dashed lines and labeled, as follows. The numbers 1 and 2 correspond to P1 and P2 domains with polar axes [111] and [\(\overline{1}\overline{1}\)1], respectively. The characters a and b correspond to the phase boundary of the SkL state (SkL–cycloidal and SkL–FM) and the cycloidal–FM boundary, respectively. The asterisks in b, d mark the newly found anomaly, associated with magnetic transitions at DWs.
a The solid and dashed lines are phase boundaries deduced from magneto-current and torque measurements, respectively. Triangles represent SANS data, while circles/squares correspond to magnetization measurements without/with electric field poling. Labels of the phase boundaries (1a, 1b, 2a, 2b) correspond to those in Fig. 4. Note that (a) does not exclusively contain data obtained on polar mono-domain samples, but includes all anomalies, which are present both in mono- and multi-domain samples. For multi-domain crystals, H∥ and H⊥ refers to field components parallel and perpendicular to the polar axis of the domain to which the anomalies are assigned. For the assignment of the different anomalies to different polar domains in multi-domain crystals and the establishment of the unified phase diagram, see the main text. The hashed low-field area in a indicates the region of the cycloidal q-vector reorientation, while the black crosses along the dashed black line correspond to the points where the SANS images in Fig. 3 were taken. In b, the phase boundaries, which are also present in the polar mono-domain case, are shown only as deduced from the magneto-current measurements. The additional phase boundary labeled by 1* & 2* is determined by magneto-current (sample #1: light blue lines, sample #2: dark blue lines), by torque (cyan lines) and by susceptibility measurements (blue square).
Figure 4a shows magneto-current studies on sample #1 poled into a nearly P1 mono-domain state, where all the observed anomalies, labeled as 1a and 1b, are assigned to transitions in the P1 domain with polar axis along the [111] direction, except for a faint signal, labeled as 2a. The 180° periodicity of the signal can be readily followed. In contrast, Fig. 4b shows magnetic torque data as obtained on a polar multi-domain sample. Here, the faint feature (2a), which is hardly traceable in the magneto-current data for the P1 mono-domain state, shows up clearly as a replica of the droplet-like motifs (1a), which are the strong features centered around 0° and 180° in the nearly mono-domain sample. This additional droplet is also found in magneto-current studies on sample #2 realizing a multi-domain state, as shown in Fig. 4c. It is centered at around ~109°, the angle spanned by the polar axes [111] and [\(\overline{1}\)\(\overline{1}\)1]. Thus, it originates from the P2 polar domain with its polar axis also lying in the field rotation plane. It is important to note that while for the P1 domain only the magneto-current component parallel to its polar axis (j∥) is measured and not the perpendicular component (j⊥), for the P2 domain a 1:3 mixture of j∥ and j⊥ is detected, due to the fixed contact geometry. (For additional magneto-current data on sample #2 in the P2 mono-domain state and on sample #1 in a multi-domain state, see Supplementary Figs. 2 and 3.) For multi-domain samples, the detailed angular dependence of the magneto-current and torque data reveal which magnetic anomalies can be assigned to P1 or P2 polar domains, and help to establish a domain-specific magnetic phase diagram (Fig. 5a), as if the samples were polar mono-domain. Magnetic anomalies corresponding to P3 and P4 domains cannot be unambiguously assigned, mainly because the angle spanned by the magnetic field and their polar axes varies over a limited range, 54–90°, while the field is rotated in the (1\(\overline{1}\)0) plane.
In the polar mono-domain state (Fig. 5a), there are three magnetic phases showing up, the cycloidal, the Néel-type SkL and the FM state, in accord with former studies43,51. Note that phase boundaries in Fig. 5a are displayed, from one hand, as obtained from magneto-current data on a P1 mono-domain crystal (Fig. 4a). On the other hand, Fig. 5a also shows the phase boundaries, as obtained for a single type of domain embedded in a polar multi-domain crystal, when the orientation of the field is measured from the polar axis of that type of domain. Since there is no difference between the two cases, phase boundaries in Fig. 5a are representative to the magnetic states inside the polar domains. In fields applied along the polar axis, the cycloidal phase has coexisting domains with wavevectors oriented in different directions (in the plane perpendicular to the rhombohedral axis) up to its transformation to the SkL state42,43. By oblique fields, this cycloidal multi-domain state is turned to a cycloidal mono-domain state, since H⊥ selects the unique q-vector, which is perpendicular to this field component43. This repopulation of the cycloidal domains is directly detected by SANS experiments (see Supplementary Fig. 4) and also manifested in magnetic susceptibility and magneto-current data as a low-field upturn and a peak, respectively, at H⊥ ~ 40 mT, as discerned, e.g., in Fig. 6a, b. (For details see Supplementary Fig. 5.) The crossover regime from the cycloidal multi- to mono-domain state is also indicated in Fig. 5a. Another important observation is that for certain angles of oblique fields, there is a re-entrant cycloidal state, where the full sequence of magnetic transitions with increasing field is cycloidal → SkL → cycloidal → FM. This re-entrance of the cycloidal phase, found in magnetization, magneto-current and torque experiments for ϕ = 21–29°, has been predicted for oblique fields in GaV4Se852, but has not been observed yet43,51.
Magnetic field dependence of a, the real part of the ac susceptibility, b the magneto-current density, c the dissipative part of the torque, and d the SANS intensity, all measured in H∥ [001] (ϕ ~ 54°). Black/red curves were recorded on polar multi-/mono-domain crystals. The inset in a shows a magnified view of the anomaly around 100 mT for three different electric poling fields (red: +2.5 \(\frac{{\rm{kV}}}{{\rm{cm}}}\), green: 0 \(\frac{{\rm{kV}}}{{\rm{cm}}}\), black: −2.5\(\frac{{\rm{kV}}}{{\rm{cm}}}\)). The brown, blue, and red vertical dashed lines indicate the q-vector re-orientation, the anomaly observed in multi-domain samples and the cycloidal → FM transition, respectively. b Displays data for both sample #1 and #2 in mono- and multi-domain states.
Magnetic transition only observed in multi-domain crystals
In polar multi-domain states, besides the features assigned to magnetic transitions within the different types of polar domains, there are additional anomalies in the torque and magneto-current data, marked by asterisks in Fig. 4b, d, respectively. In case of magneto-current measurements, the corresponding angular range is highlighted by a rectangle in Fig. 4c and a zoom-in view of the magneto-current curves is given in Fig. 4d. In the torque data, there are additional weak features observed (Poggio, unpublished). However, here we only discuss anomalies simultaneously discerned in magnetization, magneto-current and torque data.
The key observation of the present work is the emergence of this additional magnetic transition in polar multi-domain samples, as shown in Fig. 5b. This change in the magnetic state is triggered by oblique fields and located in the middle of the cycloidal phase, where the cycloidal modulation with a unique q-vector is already established by the H⊥ component of the field. Figure 6 summarizes the signatures of this extra transition, based on various quantities measured in H∥[001]. This choice of the field orientation guarantees that all types of polar domains host the same magnetic state, irrespective of the magnitude of the field, since the [001] axis spans the same angle (54°) with the magnetic anisotropy axes of all the four types of polar domains. Thus, one would expect the same magnetic anomalies, irrespective of having a polar mono- or multi-domain sample, unless the presence of DWs introduces an additional magnetic state not existing inside the domains. The magnetic susceptibility has a sharp peak at ~100 mT for a polar multi-domain sample, which is strongly suppressed as the polar mono-domain state is approached by poling, though not fully achieved. We succeeded with more efficient poling in the magneto-current studies: Sharp steps in the magneto-current curves associated with this transition are clearly resolved on sample #1 and #2 with multi-domain states, while these anomalies are completely suppressed for both samples, when either the P1 or P2 mono-domain state is reached. This means that both j∥ and j⊥ show an anomaly at ~100 mT only in multi-domain samples. The dissipative part of the magnetic torque signal also shows a weak anomaly at this field, though it is better visible a few degrees away from the [001] direction. In this case the mono-domain state could not be studied due to the unfeasibility of electric poling. In the field dependence of the SANS intensity we could not observe any anomaly associated with this transition. This may be due to the signal to noise ratio and the limited field resolution in the SANS measurements.
The weakness of this magnetization anomaly also implies that it is associated with magnetic states confined to DWs. Namely, the jump in the magnetization, corresponding to the susceptibility peak observed at 100 mT with H∥[001], is <5% of the magnetization step observed upon the cycloidal to SkL transition in similar fields for H∥[111] (See Supplementary Fig. 6).
Another possibility would be that while the anomaly is only present in multi-domain crystals, as demonstrated by electric poling experiments, it is associated to a novel magnetic state triggered by but not confined to the DWs. However, in this case a broad anomaly is expected due to the large variation of the DW separation. In contrast, it is rather sharp with a full width of ≲3 mT. We can similarly exclude that this anomaly originates from DW pinning, domain–domain interactions or defects, as they cannot lead to a sharp transition, with a well-reproducible critical field in different multi-domain crystals. Moreover, the cycloidal mono-domain state within the polar domains is already established at lower magnetic fields, as it is clear from the hashed area in Fig. 5a, indicating the region where the cycloidal q-vector reorientation takes place.
Discussion
Our study demonstrates that the existence of DWs is a prerequisite for the emergence of the new magnetic state in GaV4Se8, as revealed by macroscopic magnetic and magnetoelectric properties. The density of DWs is rather high in this compound, especially if we compare the typical DW distance of ~100–500 nm to the wavelength of the Néel-type magnetic modulations of ~20 nm. The DWs in this compound do not only produce a sudden change in the direction of the magnetic anisotropy axis, but also change the orientation of the Dzyaloshinskii–Moriya vectors. We think that the mismatch between different modulated states, favored by different magnetic interactions at adjacent domains, can give rise to the formation of new spin textures at the DWs.
The magnetic frustration coming from the change in the Dzyaloshinskii–Moriya interaction at DWs should also suppress the stability range of the modulated states near DWs. It is because the critical magnetic field, where the modulated states transform to the FM state, scales with D2/J, where D is the strength of the Dzyaloshinskii–Moriya interaction and J is the isotropic Heisenberg exchange.
The corresponding scenario for the magnetic anomaly, observed exclusively in polar multi-domain samples, is that the DW-confined magnetic textures become FM at lower fields, when the cycloidal modulations still persist inside the domains. For that case, one can roughly estimate the extension of the confined magnetic states perpendicular to the DWs based on the average separation of the planar DWs and the typical magnitude of the magnetization jump observed at 100 mT in multi-domain crystals, which are ~300 nm and ~1% of the saturation magnetization, respectively. By assuming that the magnetic texture at the DW is switched from a conical state—with a uniform magnetization at least as large as in the bulk—to the fully polarized FM state, the volume fraction of the DW-confined states is estimated to be 1–2%. This yields an effective thickness of ~3–6 nm for the DW-confined magnetic states, which is somewhat smaller than the cycloidal pitch in the bulk (~20 nm). While the anomaly is clearly linked to the presence of polar DWs, in principle it may indicate the onset of DW-confined states instead of their transformation to the FM state. In this case, the DW-confined states must transform to the FM state at the same time as the cycloidal to FM transition happens inside the domains, due the lack of a second weak anomaly in Fig. 5b.
It is important to note that the two transition lines 1* and 2* in Fig. 4d fall on each other and form a single phase boundary in Fig. 5b, if they are respectively assigned to P1 and P2 domains, meaning that the angle of the magnetic field is measured from the corresponding polar axes. From this, we conclude that these confined magnetic states do not form at DWs between P1 and P2 domains, but at P1–P3 or P2–P4 DWs parallel to the (100) plane or at P1–P4 or P2–P3 DWs parallel to the (010) plane. As discussed earlier, the magnetic anisotropy axis of each domain spans the same angle with the field for H∥[001], thus, the same magnetic state exists inside all the four polar domains. In contrast, not all the DWs are magnetically equivalent for this specific field orientation: H∥[001] lies within the plane of the four types of DWs listed above and is perpendicular to the P1–P2 and P3–P4 DWs. Note that in the broad angular range, where the new state appears at the DWs, the corresponding domains host cycloids with different spin rotation planes. Thus, the edge state likely emerges as a consequence of imperfect matching of two cycloids. (For a schematic representation of the edge states, see Supplementary Fig. 7). A similar phenomenon has recently been observed for antiferromagnetic spin cycloids interfaced at polar DWs of BiFeO353,54. To reveal the spin texture of the new magnetic state requires real-space magnetic imaging, which seems to be highly challenging in GaV4Se8.
Recently, the influence of structural DWs on macroscopic (bulk) electronic properties has been extensively investigated20,23. In contrast, manifestations of spin textures confined to DWs in macroscopic magnetic properties have hardly been observed. In the present work, we found sharp magnetic and magnetoelectric anomalies in GaV4Se8 that we assign to a phase transition originating from magnetic states confined to polar DWs. Our rough estimate, based on the DW density and the observed magnetization jump, indicates that these states are confined to a ~3–6 nm wide vicinity of the DWs. On the basis of our finding, we anticipate that magnetic materials hosting structural DWs can generally provide a fertile ground for novel forms of magnetism.
Methods
Sample synthesis and characterization
Single crystals of GaV4Se8 with typical mass of 1–30 mg were grown by the chemical vapor transport method using iodine as the transport agent. The crystallographic orientation of the samples was determined by X-ray Laue and neutron diffraction.
Scanning probe microscopy
Scanning probe microscopy was performed on an Omicron low-temperature ultra-high vacuum atomic force microscope equipped with RHK Technology Inc. R9-controller electronics using Nanosensor SSS-QMFMR probes (spring constant k ≈ 3.4 N/m, resonance frequency f0 ≈ 77.7 kHz) for magnetic measurements as well as PtSi-FM probes (spring constant k ≈ 2.5 N/m, resonance frequency f0 ≈ 73.3 kHz) for all other measurements. Non-contact measurements were done at a frequency shift of Δf = −100 Hz, the oscillation amplitude was controlled to 10 nm, and local differences of the contact potential were compensated by running a Kelvin-probe force controller.
For MFM, the magnetization direction of the tip was fixed by applying a large magnetic field along the z direction. Images were recorded in a two-step process. Firstly, the topography of the sample was measured, and the two-dimensional slope was balanced. Secondly, the MFM tip was retracted by ~30 nm in order to record the magnetic forces only, while scanning the sample surface in the area of interest.
Frequency-modulated Kelvin-probe force microscopy (FM-KPFM) allows the determination of the local contact potential difference simultaneously to topography and dissipation in non-contact mode55,56,57. Typically, the Kelvin modulation voltage together with the dc compensation bias was applied to the tip with an amplitude of 5 V and a frequency of 4.1 kHz, while a bias of −145 V was applied to the sample backside. The resulting sideband in the cantilever motion spectrum is directly detected with a lock-in amplifier within the R9-controller electronics running at the detected cantilever frequency plus the applied modulation frequency. Nullifying the detected sideband signal by application of a bias to the tip allows compensating the conservative electrostatic forces and simultaneously quantifies the contact potential difference between tip and sample.
Data were analyzed with the Gwyddion software.
Magnetization measurements
The magnetization and ac-susceptibility measurements were performed following an initial zero-field cooling, using a magnetic property measurement system (MPMS) from quantum design. For ac-susceptibility measurements with electric field poling, a home made probe was used. Poling electric field was applied only during cooling.
Magneto-current measurements
For the pyro- and magneto-current measurements, contacts on two-parallel (111) faces of the crystals were applied using silver paint. The sample was cooled using an Oxford helium-flow cryostat. For changing the orientation of the magnetic field with respect to the electric contacts, the sample was mounted on a platform, which can be rotated by a stepper motor. To ensure low-noise measurements, the platform was equipped with two coaxial cables. For magneto-current measurements, the current was recorded using Keysight B2987A electrometer while the magnetic field was swept with a typical rate of 0.5–1 T/min. For pyrocurrent measurements, the current was recorded with the same electrometer while the temperature was swept from 3 to 50 K with a rate of about 6 K/min.
Torque magnetometry
Torque data were recorded with dynamic cantilever magnetometry (DCM)29,58. A single crystalline piece of GaV4Se8 (spacial dimensions in the order of 100 μm) was attached to the end of a commercial cantilever (Arrow-TL1, Nanoworld). In DCM, the cantilever is driven into self-oscillation at its resonance frequency. Changes in the dissipation ΔΓ = Γ − Γ0, induced by the torque from the sample, are measured as a function of the uniform applied magnetic field H, where Γ0 is the cantilever’s intrinsic mechanical dissipation at H = 0. Measurements of ΔΓ are particularly useful for identifying magnetic phase transitions29.
DCM measurements were carried out in a vibration-isolated closed-cycle cryostat. The pressure in the sample chamber is <10−6 mbar and the temperature can be stabilized between 4 and 300 K. Using an external rotatable superconducting magnet, magnetic fields up to 4.5 T can be applied along any direction spanning 120° in the plane of cantilever oscillation. A piezoelectric actuator mechanically drives the cantilever with a constant oscillation amplitude of a few tens of nanometers using a feedback loop implemented by a field-programmable gate array. The cantilever’s motion is read out using an optical fiber interferometer using 100 nW of laser light at 1550 nm59.
Small-angle neutron scattering
SANS was performed on a 11.6 mg single crystal sample of GaV4Se8. SANS patterns discussed in the main text were measured using the SANS-I instrument of SINQ at the Paul Scherrer Institut (PSI), Villigen, Switzerland. The wavelength of the incoming neutrons was 6 Å, the collimation and the sample-detector distances were set to 6 m. The magnetic field was applied in various directions within the (1\(\overline{1}\)0) plane. In addition, magnetic field dependence of the scattering data shown in the supplement was measured using the D11 and the D33 instruments at the Institut Laue-Langevin (ILL), Grenoble, France. The neutron wavelength of 5 Å was selected and the collimator-sample and the sample-detector distances were set to 5 m. In all experiments the sample together with the magnet is rotated and tilted, i.e., rocked in order to move the magnetic diffraction peaks through the Ewald sphere. The SANS patterns presented are the sum of intensities through the whole rocking angle range. Similar measurements were taken in the paramagnetic phase at 20 K, and subtracted from the data to obtain the magnetic scattering data.
Data availability
The measurement data from ILL are publicly available under the ILL DOI-s https://doi.org/10.5291/ILL-DATA.INTER-338 and https://doi.org/10.5291/ILL-DATA.5-42-438. The rest of the data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Resnick, D. J., Garland, J. C., Boyd, J. T., Shoemaker, S. & Newrock, R. S. Kosterlitz-Thouless transition in proximity-coupled superconducting arrays. Phys. Rev. Lett. 47, 1542–1545 (1981).
Ohtomo, A. & Hwang, H. Y. A high-mobility electron gas at the LaAlO3 /SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Wang, Q.-Y. et al. Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Chin. Phys. Lett. 29, 037402 (2012).
He, S. et al. Phase diagram and electronic indication of high-temperature superconductivity at 65 K in single-layer FeSe films. Nat. Mater. 12, 605–610 (2013).
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007).
Nakamura, J. et al. Aharonov-Bohm interference of fractional quantum Hall edge modes. Nat. Phys. 15, 563–569 (2019).
Cohen, Y. et al. Synthesizing a ν = 2/3 fractional quantum Hall effect edge state from counter-propagating ν = 1 and ν = 1/3 states. Nat. Commun. 10, 1920 (2019).
MacDonald, A. H. Edge states in the fractional-quantum-Hall-effect regime. Phys. Rev. Lett. 64, 220–223 (1990).
Andrei, E. Y. et al. Observation of a magnetically induced Wigner solid. Phys. Rev. Lett. 60, 2765–2768 (1988).
Shapir, I. et al. Imaging the electronic and Wigner crystal in one dimension. Science 364, 870–875 (2019).
Zurek, W. H. Cosmological experiments in superfluid helium? Nature 317, 505–508 (1985).
Choi, T. et al. Insulating interlocked ferroelectric and structural antiphase domain walls in multiferroic YMnO3. Nat. Mater. 9, 253–258 (2010).
Chae, S. C. et al. Self-organization, condensation, and annihilation of topological vortices and antivortices in a multiferroic. Proc. Natl. Acad. Sci. USA 107, 21366–21370 (2010).
Lilienblum, M. et al. Ferroelectricity in the multiferroic hexagonal manganites. Nat. Phys. 11, 1070–1073 (2015).
Ma, J. et al. Controllable conductive readout in self-assembled, topologically confined ferroelectric domain walls. Nat. Nanotechnol. 13, 947–952 (2018).
Seidel, J. Topological Structures in Ferroic Materials (Springer, New York, 2016).
Butykai, Á. et al. Characteristics of ferroelectric-ferroelastic domains in Néel-type skyrmion host GaV4S8. Sci. Rep. 7, 44663 (2017).
Farokhipoor, S. et al. Artificial chemical and magnetic structure at the domain walls of an epitaxial oxide. Nature 515, 379–383 (2014).
Ruff, E. et al. Conductivity contrast and tunneling charge transport in the vortexlike ferroelectric domain patterns of multiferroic hexagonal YMnO3. Phys. Rev. Lett. 118, 036803 (2017).
Schaab, J. et al. Electrical half-wave rectification at ferroelectric domain walls. Nat. Nanotechnol. 13, 1028–1034 (2018).
Seidel, J. et al. Conduction at domain walls in oxide multiferroics. Nat. Mater. 8, 229–234 (2009).
Werner, C. S. et al. Large and accessible conductivity of charged domain walls in lithium niobate. Sci. Rep. 7, 9862 (2017).
Matzen, S. et al. Super switching and control of in-plane ferroelectric nanodomains in strained thin films. Nat. Commun. 5, 4415 (2014).
Kan, D. et al. Tuning magnetic anisotropy by interfacially engineering the oxygen coordination environment in a transition metal oxide. Nat. Mater. 15, 432–437 (2016).
Liao, Z. et al. Controlled lateral anisotropy in correlated manganite heterostructures by interface-engineered oxygen octahedral coupling. Nat. Mater. 15, 425–431 (2016).
Yu, X. Z. et al. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 10, 106–109 (2011).
Sonntag, A., Hermenau, J., Krause, S. & Wiesendanger, R. Thermal stability of an interface-stabilized skyrmion lattice. Phys. Rev. Lett. 113, 077202 (2014).
Mehlin, A. et al. Stabilized skyrmion phase detected in MnSi nanowires by dynamic cantilever magnetometry. Nano Lett. 15, 4839–4844 (2015).
Zheng, F. et al. Experimental observation of chiral magnetic bobbers in B20-type FeGe. Nat. Nanotechnol. 13, 451–455 (2018).
Reschke, S. et al. Optical conductivity in multiferroic gav4s8 and gev4s8: Phonons and electronic transitions. Phys. Rev. B 96, 144302 (2017).
Reschke, S. et al. Lattice dynamics and electronic excitations in a large family of lacunar spinels with a breathing pyrochlore lattice structure. Phys. Rev. B 101, 075118 (2020).
Abd-Elmeguid, M. M. et al. Transition from Mott insulator to superconductor in GaNb4 Se8 and GaTa4Se8 under high pressure. Phys. Rev. Lett. 93, 126403 (2004).
Phuoc, V. T. et al. Optical conductivity measurements of GaTa4Se8 under high pressure: Evidence of a bandwidth-controlled insulator-to-metal Mott transition. Phys. Rev. Lett. 110, 037401 (2013).
Guiot, V. et al. Avalanche breakdown in GaTa4Se8−xTex narrow-gap Mott insulators. Nat. Commun. 4, 1722 (2013).
Dorolti, E. et al. Half-metallic ferromagnetism and large negative magnetoresistance in the new lacunar spinel GaTi3VS8. J. Am. Chem. Soc. 132, 5704–5710 (2010).
Kim, H.-S., Im, J., Han, M. J. & Jin, H. Spin-orbital entangled molecular jeff states in lacunar spinel compounds. Nat. Commun. 5, 3988 (2014).
Singh, K. et al. Orbital-ordering-driven multiferroicity and magnetoelectric coupling in GeV4S8. Phys. Rev. Lett. 113, 137602 (2014).
Wang, Z. et al. Polar dynamics at the Jahn-Teller transition in ferroelectric GaV4S8. Phys. Rev. Lett. 115, 207601 (2015).
Geirhos, K. et al. Orbital-order driven ferroelectricity and dipolar relaxation dynamics in multiferroic GaMo4S8. Phys. Rev. B. 98, 224306 (2018).
Ruff, E. et al. Polar and magnetic order in GaV4Se8. Phys. Rev. B. 96, 165119 (2017).
Kézsmárki, I. et al. Néel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8. Nat. Mater. 14, 1116–1122 (2015).
Bordács, S. et al. Equilibrium skyrmion lattice ground state in a polar easy-plane magnet. Sci. Rep. 7, 7584 (2017).
Butykai, Á. et al. Squeezing magnetic modulations by enhanced spin-orbit coupling of 4d electrons in the polar semiconductor GaMo4S8. Preprint at https://arxiv.org/abs/1910.11523 (2019).
Pocha, R., Johrendt, D. & Pöttgen, R. Electronic and structural instabilities in GaV4S8 and GaMo4S8. Chem. Mater. 12, 2882–2887 (2000).
Hlinka, J. et al. Lattice modes and the Jahn-Teller ferroelectric transition of GaV4S8. Phys. Rev. B. 94, 060104 (2016).
Bogdanov, A. N. & Yablonskii, D. A. Thermodynamically stable “vortices” in magnetically ordered crystals. The mixed state of magnets. Zh. Eksp. Teor. Fiz. 95, 178–180 (1989).
Neuber, E. et al. Architecture of nanoscale ferroelectric domains in GaMo4S8. J. Phys.-Condens. Mat. 30, 445402 (2018).
Ehlers, D. et al. Exchange anisotropy in the skyrmion host GaV4S8. J. Phys.-Condens. Mat. 29, 065803 (2017).
Ehlers, D. et al. Skyrmion dynamics under uniaxial anisotropy. Phys. Rev. B. 94, 014406 (2016).
Fujima, Y., Abe, N., Tokunaga, Y. & Arima, T. Thermodynamically stable skyrmion lattice at low temperatures in a bulk crystal of lacunar spinel GaV4Se8. Phys. Rev. B. 95, 180410 (2017).
Leonov, A. O. & Kézsmárki, I. Skyrmion robustness in noncentrosymmetric magnets with axial symmetry: the role of anisotropy and tilted magnetic fields. Phys. Rev. B. 96, 214413 (2017).
Chauleau, J.-Y. et al. Electric and antiferromagnetic chiral textures at multiferroic domain walls. Nat. Mater. 19, 386–390 (2020).
Xue, F., Yang, T. & Chen, L.-Q. Electric-field-induced switching dynamics of cycloidal spins in multiferroic BiFeO3: phase-field simulations. Preprint at https://arxiv.org/abs/1911.04023 (2019).
Weaver, J. M. R. & Abraham, D. W. High resolution atomic force microscopy potentiometry. J. Vac. Sci. Tecnol. B 9, 1559–1561 (1991).
Nonnenmacher, M., O’Boyle, M. P. & Wickramasinghe, H. K. Kelvin probe force microscopy. Appl. Phys. Lett. 58, 2921–2923 (1991).
Zerweck, U., Loppacher, C., Otto, T., Grafström, S. & Eng, L. M. Accuracy and resolution limits of Kelvin probe force microscopy. Phys. Rev. B. 71, 125424 (2005).
Gross, B. et al. Dynamic cantilever magnetometry of individual CoFeB nanotubes. Phys. Rev. B. 93, 064409 (2016).
Rugar, D., Mamin, H. J. & Guethner, P. Improved fiber-optic interferometer for atomic force microscopy. Appl. Phys. Lett. 55, 2588–2590 (1989).
Acknowledgements
We thank Á. Butykai for stimulating discussions. This work was supported by the DFG via the Transregional Research Collaboration TRR 80 From Electronic Correlations to Functionality (Augsburg/Munich/Stuttgart), via the Collaborative Research Center Correlated Magnetism: From Frustration to Topology (CRC1143) project no. 247310070, via the Center of Excellence—Complexity and Topology in Quantum Matter (ct.qmat)—EXC 2147, and via the DFG Priority Program SPP2137, Skyrmionics, under Grant Nos. KE 2370/1-1, EN 434/40-1, EN 434/38-1, MI 2004/3-1; by the Hungarian National Research, Development and Innovation Office NKFIH, ANN 122879 BME-Nanonotechnology FIKP grant (BME FIKP-NAT), by the Swiss National Science Foundation via Grants No. 200020-159893, the Sinergia network Nanoskyrmionics (Grant No. CRSII5-171003) the NCCR Quantum Science and Technology (QSIT).
Author information
Authors and Affiliations
Contributions
V.T. synthetized the crystals; B.G., A.M., S.P., and M.P. performed and analysed the torque measurements; K.G. and P.L. performed and analysed the pyro- and magneto-current measurements; B.G.Sz., S.B., J.S.W., R.C., and I.K. performed and analysed the SANS measurements; S.G. and S.W. performed and analysed the magnetization measurements; E.N., D.I., and P.M. performed and analyzed the AFM measurements; I.K. wrote the manuscript with contributions from K.G., A.O.L., P.M., and L.M.E.; I.K., M.P., and S.B. planned the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Geirhos, K., Gross, B., Szigeti, B.G. et al. Macroscopic manifestation of domain-wall magnetism and magnetoelectric effect in a Néel-type skyrmion host. npj Quantum Mater. 5, 44 (2020). https://doi.org/10.1038/s41535-020-0247-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0247-z
This article is cited by
-
Squeezing the periodicity of Néel-type magnetic modulations by enhanced Dzyaloshinskii-Moriya interaction of 4d electrons
npj Quantum Materials (2022)
-
Slowdown of photoexcited spin dynamics in the non-collinear spin-ordered phases in skyrmion host GaV4S8
Nature Communications (2022)
-
Giant conductivity of mobile non-oxide domain walls
Nature Communications (2021)
-
Vital role of magnetocrystalline anisotropy in cubic chiral skyrmion hosts
npj Quantum Materials (2021)