Abstract
The downscaling of silicon-based structures and proto-devices has now reached the single-atom scale, representing an important milestone for the development of a silicon-based quantum computer. One especially notable platform for atomic-scale device fabrication is the so-called Si:P δ-layer, consisting of an ultra-dense and sharp layer of dopants within a semiconductor host. Whilst several alternatives exist, it is on the Si:P platform that many quantum proto-devices have been successfully demonstrated. Motivated by this, both calculations and experiments have been dedicated to understanding the electronic structure of the Si:P δ-layer platform. In this work, we use high-resolution angle-resolved photoemission spectroscopy to reveal the structure of the electronic states which exist because of the high dopant density of the Si:P δ-layer. In contrast to published theoretical work, we resolve three distinct bands, the most occupied of which shows a large anisotropy and significant deviation from simple parabolic behaviour. We investigate the possible origins of this fine structure, and conclude that it is primarily a consequence of the dielectric constant being large (ca. double that of bulk Si). Incorporating this factor into tight-binding calculations leads to a major revision of band structure; specifically, the existence of a third band, the separation of the bands, and the departure from purely parabolic behaviour. This new understanding of the band structure has important implications for quantum proto-devices which are built on the Si:P δ-layer platform.
Similar content being viewed by others
Introduction
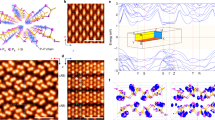
Si:P δ-doping offers potential for the realisation of true atomic-scale components for quantum computer applications1,2,3,4,5,6,7,8, whilst retaining compatibility with the simple processing, stability, and technological relevance of silicon. Understanding, manipulating, and controlling the properties of Si:P δ-layers, has therefore been the centre of an intense research effort, however, a real understanding of the electronic structure has remained elusive. Density functional theory (DFT) calculations and angle-resolved photoemission spectroscopy (ARPES) recently shed new light on these systems, giving the first glimpse of their electronic structure9,10,11,12,13,14,15,16,17,18: the metallic nature of Si:P δ-layers was believed to originate from two nearly-parabolic states, called 1Γ and 2Γ, dispersing across the Fermi level (EF) as a consequence of the strong electronic confinement created by the P dopants in the semiconducting Si bulk (see Fig. 1a, b). The energy separation of these states, which is called valley-splitting14, together with their many-body interactions15 is responsible for transport properties in this material system and ultimately the function of Si:P δ-layer-based quantum electronic devices.
a Schematic of the δ-layer sample and b the symmetric doping potential centred around the position of the P dopant plane. The strong potential created by the P atoms confines the conduction band, developing a 2D electronic structure which has been understood to be comprised of two states, labelled 1Γ (red) and 2Γ (blue). c The Brillouin Zone (BZ) of silicon showing the directions relevant for this work. The blue dashed lines show the 2D BZ, and the pink shading and lines show a 2D slice through the 3D BZ of silicon at the relevant value of kz for this work (darkest shade: 1st bulk BZ). The high symmetry directions kx, ky (red axes), and kxy (black axis) are also indicated. d Tight-binding calculations (following ref. 10) showing the 1Γ and 2Γ states dispersing across EF (with EF adjusted such that the minimum of the dispersion matches with the data in panels (f) and (g)) along the kxy and kx (or ky) directions (blue and green markers, respectively). e ARPES acquisition of a ‘dummy’ Si sample (i.e., Si bulk plus 2 nm epitaxial overlayer, but without the P dopant δ-layer), showing the absence of any states around EF. f ARPES acquisition along the kxy direction showing only two states. A momentum distribution curve (MDC) at the EF shows no presence of additional states. g ARPES measurement along the kx (or ky) direction showing the existence of three states, (marked with blue, red, and yellow lines to serve as a guide for the eye). As discussed in the main text, the agreement between the TB calculation (d) and the ARPES data in panels (f) and (g) is unsatisfactory. h An energy-dependent curve integrated in the range k∥ = 0 ± 0.015 Å−1, further confirming the occupied nature of the 3rd state. All ARPES measurements are performed using hν = 36 eV13,15.
In this work, we show that important details of the electronic band structure were previously reported incorrectly. We reveal the presence of additional anisotropic electronic states crossing EF, resolved only for specific directions in the BZ (see Fig. 1f, g). Whilst in the diagonal direction (kxy) only two electronic states can be seen, along the axial directions (kx and ky), a clear three-band structure is resolved which has not been predicted. The original 1Γ appears to actually consist of two sub-bands, indicated by the red and yellow parabolae in Fig. 1g. The presence of three states across EF cannot be reconciled with published DFT9,11,12 and tight-binding (TB) calculations10. This discrepancy is also seen in our TB calculations (Fig. 1d and see Supplementary Information), where only two bands, instead of three, are responsible for the metallic properties of the system. This opens an interesting question about the origin of the sub-band structure resolved by ARPES, as all the states which contribute to this sub-band structure are expected to contribute to the transport properties of Si:P δ-layers.
We examine some ingredients which have previously been ignored, such as spin–orbit coupling (SOC), the role of the dielectric constant, ϵ, and an asymmetric doping profile, to explain the origin of this sub-band structure. [Note: Although reports of SOC in Si:P δ-layers are generally absent, studies of SOC in Si:P derived structures do exist19.] We show that ϵ is expected to be dramatically increased in the vicinity of the high-density dopant layer, thereby causing a large increase in the efficiency of the screening. This causes the confinement to be stronger than previously expected, and hence for additional states originally predicted to be well above EF (as in Fig. 1d) to become occupied.
Discussion and results
Before further discussing the origin of the fine structure of Si:P δ-layers, we first present a qualitative discussion of the electronic structure and the parameters to which it is sensitive. First of all, the available calculations have predicted two nearly parabolic bands with a valley splitting of ≈30 meV9,10,11,12. It is worth noting that this value is somewhat controversial, and depends on a number of parameters within the model, such as the order/disorder of the dopants11. Our measurements reveal the presence of three bands, of which the most occupied bands have a valley splitting which is too small to resolve experimentally (i.e., <35 meV). In other words, the observed valley splitting is either small or zero. Furthermore, in the axial kx and ky directions, the dispersion of the most occupied band deviates significantly from parabolic behaviour, whereas in the diagonal direction (labelled kxy) the dispersion of these bands is very close to parabolic, and they appear to either be degenerate or to have a very small separation. The state with its minimum closest to the Fermi level (i.e., the blue parabola in Fig. 1f, g) is separated from the other bands by ≈220 meV, which is very large compared to our TB calculated valley splitting. In other words, it is unclear which of the three bands (if any) correspond to the calculated 1Γ and 2Γ. It is especially unclear whether the additional band is split off from 1Γ, or whether it actually corresponds to the calculated 2Γ (thereby implying that the least occupied band has another origin). In any case, it is clear that the calculated band structure deviates significantly from the experimentally observed band structure.
In principle, symmetry breaking in one form or another could give rise to additional bands. More specifically, the in-plane dopant order/disorder is not well known in practice, but is thought to influence the electronic structure18. In any case, whilst the band structure is influenced by the symmetry and ordering of the dopants, this is not able to account for the observed behaviour (see Supplementary Information).
This notion that dopant ordering is not a significant factor is also supported empirically: We have prepared three different δ-layer samples, in which the dopant ordering is dissimilar, however the electronic structure remains very similar. The spectra in Fig. 2a correspond to a ‘standard’ single-dose Si:P δ-layer with <1/4 of a monolayer (ML) of P dopants in an almost atomically sharp plane. Figure 2b corresponds to a similarly sharp ‘double dose’ with dopant density >1/4 ML and increased disorder20. Figure 2c corresponds to a ‘thick’ (1.5 nm) region with a similar (i.e., ≈25%) doping concentration (see Supplementary Information).
Fermi surface and electronic structures along the kxy and ky directions for a Si:P δ-layer grown with a P concentration a slightly less than 1/4 monolayer (ML), b more than 1/4 ML, and c by depositing P and Si together such to form a thicker layer (≈1.5nm) with a similar (≈25%) doping concentration. Blue, red, and yellow lines to serve as a guide for the eye. ARPES measurements are performed using hν=36eV13,15.
The measured band structure is very similar for all three preparations: The electronic structures of Fig. 2 map onto each other very well, needing only a small shift of the bands, to account for the different degrees of doping. Perhaps the most significant difference is that the least occupied band is shifted above the Fermi level when the doping density is lowest. The similarity of the band structure for these three different growth methods indicates that dopant ordering alone cannot be responsible for the mysterious third band.
Symmetry breaking (specifically, the breaking of in-plane inversion symmetry by the dopants in the δ-layer) together with SOC will lift degeneracy and thus give rise to bands which are non-degenerate with respect to their spin21,22. This could lead to 1Γ having two branches, with no splitting at k∥ = 0, anisotropic splitting at larger k∥, and a band structure which qualitatively matches the ARPES measurements. However, the expected energy splitting due to SOC is about 120× smaller than the observed energy separation of the two most occupied bands (refs. 23,24 and see Supplementary Information). We therefore discount SOC as a possible origin of the observed band structure.
Another possible factor which modifies the electronic structure is strain. By replacing a Si atom with a P dopant, some degree of strain will be introduced. On the other hand, Si (Z = 14) and P (Z = 15) are similar in size, and hence the strain is small: For Si:P δ-layers, the strain has been estimated to be between 0.1 and 0.9%9,12 (whereas the change in Si–P bond length for an isolated P dopant in an Si host is reported to be 1.7%25). This small degree of strain is insufficient to describe the existence of an extra band in the measured band structure (see Supplementary Information).
On the other hand, the modification of the dielectric constant ϵ in the vicinity of the δ-layer is surprisingly important and can significantly influence the electronic structure. The reason that δ-layer causes 2D electronic states to exist at all is because of the confinement caused by the layer of dopant atoms (see for example, Fig. 1b). The number of occupied states, and the energy separation of the states is directly related to the strength of the confining potential. The sharpness of this confinement potential strongly depends on the effectiveness of the screening within the vicinity of the δ-layer, and this in turn depends on the carrier density. Therefore, in order to describe the potential well, the screening (i.e., dielectric constant) needs to be well described. Since a larger dielectric constant is associated with more efficient screening. This means that the quantum well is less confined than previously thought (for example, ref. 10) and as a result, the splitting between some of the bands is reduced, and more bands become occupied.
For the moderate doping densities found in semiconducting Si wafers, ϵ is typically considered to be independent of dopant concentration, but for the extreme doping around the δ-layer, this view is no longer valid28: As the dopant density is increased, a subsequent increase in the susceptibility of the material, and thus in ϵ can be expected26,27,29. Following ref. 28, it is possible to estimate ϵ as a function of dopant density (ND, in units of cm−3), for P dopants in Si:
For the case of Si:P δ-layers, the 2D doping concentration is known to be close to 1/4 ML. Whilst there is some uncertainty involved in converting the 2D concentration to a 3D concentration, this problem has been addressed previously (see, for example refs. 20,30,31). Previous works suggest that in the vicinity of the δ-layer ND is 2 × 1020 cm−3 20,31, and our own previous work30 suggests that whilst the peak concentration is ≈6 × 1020 cm−3. However, we agree that the average concentration within 2–4 nm of the layer is ≈2 × 1020 cm−3. Using Eq. (1), we can therefore estimate that for ND = 2 × 1020 cm−3, ϵ ≈ 38, however at the peak of ND ≈ 6 × 1020 cm−3 it is conceivable that near to the dopant plane, ϵ could be as high as 70. In any case, it is clear that the dielectric constant may be several times higher than the value for weakly doped bulk Si.
We also point out that the role of the dielectric constant in the Slater–Koster TB theory is not the same as in ab-initio DFT. In DFT, typically the core and the valence electrons are considered, and the electronic density is computed by populating all these electronic states up to the Fermi level through self-consistent iteration of the Kohn–Sham equations. Hence, a dielectric constant of vacuum can be used, and the effective dielectric constant can be extracted from the method. In contrast, in the semi-empirical Slater–Koster TB method used here, the atomic basis functions responsible for valence bonding only are optimised to reproduce the bulk band-structure of the material without performing any self-consistent iterations of the charge density in the process. Hence, the Slater–Koster TB method in its original form cannot reproduce the dielectric constant of the material, and hence it is necessary to explicitly input a realistic value for ϵ in the Poisson equation. This is a standard technique in atomistic device simulations where the Poisson and Schrodinger/Green’s functions are solved self-consistently32,33,34.
The qualitative understanding is readily confirmed by TB calculations (see Fig. 3) in which ϵ has been increased only in the vicinity of the δ-layer (see Supplementary Information). Whilst it is not correct to use ϵ as a freely adjustable ‘fitting parameter’, it is interesting to see what happens if a range of values for ϵ are tested. Interestingly, by increasing ϵ the 1Γ − 2Γ valley-splitting stays roughly constant. However, an additional parabolic band minimum (identified from the calculations as 3Γ) is pulled down towards the Fermi level. For ϵ > 16, 3Γ starts to become occupied, and TB calculation looks more similar to the measured band structure. As ϵ continues to increase, additional parabolic band minima may also be pulled below the Fermi level, and for ϵ > 40, a fourth state also becomes partially occupied. [Note: In fact, this observation makes it possible to disentangle the role of strain: Even if we consider the small strain in the lattice to be important, then we expect a small change in the 1Γ − 2Γ valley splitting. However, because 3Γ arises from the higher excited orbital states of the 1Γ valley state, we expect the 1Γ − 3Γ valley splitting to be essentially unaffected by strain: i.e., the opposite behaviour to the TB calculation which includes enhancing ϵ.]
a Energy levels of 1Γ (red), 2Γ (blue), and 3Γ (black) as a function of dielectric constant. By increasing ϵ, keeping all other factors constant, the energy 1Γ−2Γ remains approximately constant. However, the separation 1Γ−3Γ significantly shrinks and the 3Γ state starts to cross EF. ϵ≈20 gives the best agreement with experimental data. b–f The k resolved TB calculations are shown for the axial kx and ky direction (green circle) and for the diagonal kxy direction (blue circle) for b ϵ=11.9 (i.e., for weakly doped Si, and consistent with previous calculations), c ϵ=14, d ϵ=20, e ϵ=40, and f ϵ=60.
It is clear that adjusting ϵ has a dramatic influence on the TB calculated band structure. Therefore, the next question to ask is ‘What is the most justifiable value to use?’ From the above simple argument of the estimated dopant density, we anticipate ϵ to be exceptionally large; i.e., in the range 38–70 (3–5 times higher than the bulk value). On the other hand, we can also use our measured ARPES data to make a self-consistent estimate, which we find to be somewhat lower. We therefore take the following approach: We perform the TB calculations for a range of values of ϵ (i.e., Fig. 3). As discussed previously, the increased values of ϵ correspond to a priori estimates of the carrier density. Since the resulting TB calculations give us full access to the electronic structure including the Fermi surface, we can use this output to estimate the filling, and hence to check that ND is consistent with the a priori assumed values. In other words, the self-consistency of the TB calculation is not implicit in the method, but by comparing the output estimate of ND with the input value of ND used to estimate ϵ, we can ensure that the carrier density, and therefore the dielectric constant and screening are indeed self-consistent. Finally, we can also ensure that these parameters match with ND extracted from the experiment.
The energy of the 1Γ, 2Γ, and 3Γ minima are plotted in Fig. 3a. By comparison with our experimental data, we find best agreement for ϵ ≈ 20: i.e., depending on the preparation, we generally observe the minimum of the most occupied state (1Γ) to be at EB ≈ 220 meV, and the minimum of the least occupied state (now assigned as 3Γ) to be at EB ≈ 40 meV. We also find good agreement with the TB electronic dispersions of Fig. 3b–d; The TB calculation indicates that the two most occupied bands (now assigned as 1Γ and 2Γ) are parabolic, with a small energy separation (30 meV) at k∥ = 0 and in the diagonal kxy direction, but have an increasing non-parabolic behaviour with increasing k in the axial x and y directions.
A value of ϵ of 20 is consistent with ND ≈ 6 × 1019 cm−3 28. Assuming that the dopant layer has a thickness of ≈0.5 nm15, this corresponds to a 2D carrier density of 1.2 × 1013. From the corresponding TB calculation with ϵ = 20 the 2D carrier density is extracted to be 7.6 × 1013 (and a similar extraction from the ARPES data gives 6 × 1013). In other words, the carrier density based on estimates of the size of the Fermi contours yields a value which is consistent with the assumption on which ϵ is based, but indicates that the carrier density is underestimated by assuming ϵ = 20 (i.e., this is a conservative estimate for ϵ). This could also be a consequence of one of the assumptions used: for example estimates of the thickness of the 2D layer vary and the conversion from 2D to 3D carrier density requires this to be known. In any case, the carrier density resulting from TB calculations for ϵ ≥ 20 is realistic.
Based on ARPES measurements and TB calculations, we conclude that the enhancement of ϵ due to the high dopant density is the origin of the additional electronic structure, however, some discrepancies with previous work remain. In previous studies on similar samples14, the 1Γ − 2Γ valley-splitting was reported to be ≈130 meV, whereas in this work, we conclude that the 1Γ − 2Γ splitting is <30 meV. Due to the lower sample quality and data quality in the earlier work, this was unresolvable and mistaken for a single band, and therefore the previously reported splitting of 130 meV presumably corresponded instead to the 1Γ (or 2Γ) to 3Γ splitting. On the other hand, this splitting is still small compared to the TB calculations and ARPES measurements here in which the 2Γ − 3Γ splitting is ≈200 meV. Whilst it is not possible to give a definitive explanation for this, we propose that it is most likely also a consequence of poorer sample quality; it is known that 1/4 ML dopant activation is only achievable when the Si surface is pristine, and that imperfections act to reduce this number. We therefore consider that the previously reported 130 meV valley splitting presumably corresponds to the (1Γ or 2Γ) to 3Γ splitting of a sample with a lower doping concentration than used in the current work.
Finally, we reiterate that a revision of the electronic structure of Si:P is necessary in which three nearly parabolic bands, 1Γ, 2Γ, and 3Γ all cross EF, contrary to only two bands as previously thought. Jointly, all three of these bands must be responsible for the transport properties of the system30,35 and carrier density. Importantly, the valley-splitting, i.e., separation between 1Γ and 2Γ seems to be relatively robust against variations in the sample preparation and can be estimated to be ≤35 meV. This is an important result which also shows how the properties of a device built upon a Si:P δ-layer platform are not dramatically affected by changes in the growth, but instead are reliable due to the robustness of the valley-splitting. Indeed, since the valley-splitting in devices built from the Si:P δ-layer platform affects the lifetime of carriers36, its correct value and interpretation is important for quantum device performance. Similarly, the presence of a third band crossing EF will have significant consequences for Si:P δ-layer-based quantum devices, and hence it is important that this is taken into consideration when developing device structures.
Methods
The ARPES measurements are carried out at the beamline I4 of the synchrotron facility ‘MAX-Lab’ (Lund, Sweden)37. The energy and momentum resolutions are better than 35 meV and 0.02 Å−1, respectively. The sample growth is monitored by low-energy-electron diffraction and X-ray photoemission spectroscopy. The temperature of the sample during data acquisitions is 100 K. The growth of the samples is carried out in situ; similarly to the growth method in refs. 13,14,15,16,17. For specific details on the growth see the Supplementary Information. The Si:P δ-doped layer’s band structure is modelled by an empirical sp3d5s* TB model coupled with the Poisson equation10 (see Supplementary Information for details about the dielectric constant).
Data availability
The datasets generated and analysed during the current study are available from the corresponding author on reasonable request.
References
Fuechsle, M. et al. A single-atom transistor. Nat. Nanotechnol. 7, 242–246 (2012).
Weber, B. et al. Ohm’s law survives to the atomic scale. Science 335, 64–67 (2012).
Zwanenburg, F. A. et al. Silicon quantum electronics. Rev. Mod. Phys. 85, 961 (2013).
Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633 (2018).
Fuechsle, M. et al. Spectroscopy of few-electron single-crystal silicon quantum dots. Nat. Nanotechnol. 5, 502–505 (2010).
Tettamanzi, G. C. et al. Probing the quantum states of a single atom transistor at microwave frequencies. ACS Nano 11, 2444–2451 (2017).
Broome, M. A. et al. Two-electron spin correlations in precision placed donors in silicon. Nat. Commun. 9, 980 (2018).
Kocj, M. et al. Spin read-out in atomic qubits in an all-epitaxial three-dimensional transistor. Nat. Nanotechnol. 14, 137–140 (2019).
Carter, D. et al. Electronic structure models of phosphorus δ -doped silicon. Phys. Rev. B 79, 033204 (2009).
Lee, S. et al. Electronic structure of realistically extended atomistically resolved disordered Si:P δ -doped layers. Phys. Rev. B 84, 205309 (2011).
Carter, D. J., Marks, N. A., Warschkow, O. & McKenzie, D. R. Phosphorus δ-doped silicon: mixed-atom pseudopotentials and dopant disorder effects. Nanotechnology 22, 065701 (2006).
Drumm, D. W. et al. Ab initio calculation of valley splitting in monolayer δ -doped phosphorus in silicon. Nanoscale Res. Lett. 8, 111 (2013).
Miwa, J. A., Hofmann, P., Simmons, M. Y. & Wells, J. W. Direct measurement of the band structure of a buried two-dimensional electron gas. Phys. Rev. Lett. 110, 136801 (2013).
Miwa, J. A. et al. Valley splitting in a silicon quantum device platform. Nano Lett. 14, 1515–1519 (2014).
Mazzola, F. et al. Determining the electronic confinement of a subsurface metallic state. ACS Nano 8, 10223–10228 (2014).
Mazzola, F. et al. Disentangling phonon and impurity interactions in δ-doped Si(001). Appl. Phys. Lett. 104, 173108 (2014).
Mazzola, F. et al. Simultaneous conduction and valence band quantization in ultrashallow high-density doping profiles in semiconductors. Phys. Rev. Lett. 120, 046403 (2018).
Carter, D. J., Warschkow, O., Marks, N. A. & McKenzie, D. R. Electronic structure of two interacting phosphorus δ-doped layers in silicon. Phys. Rev. B 87, 045204 (2013).
Weber, B. et al. Spin-orbit coupling in silicon for electrons bound to donors. npj Quantum Inf. 4, 61 (2018).
McKibbin, S. R. et al. Low resistivity, super-saturation phosphorus-in-silicon monolayer doping. Appl. Phys. Lett. 104, 123502 (2014).
Winkler, R. Spin–Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems (Springer, 2003).
Rotenberg, E., Chung, J. W. & Kevan, S. D. Spin-orbit coupling induced surface band splitting in Li/W(110) and Li/Mo(110). Phys. Rev. Lett. 82, 4066–4069 (1999).
Ferdous, R. et al. Valley dependent anisotropic spin splitting in silicon quantum dots. npj Quantum Inf. 4, 26 (2018).
Ferdous, R. et al. Interface-induced spin-orbit interaction in silicon quantum dots and prospects for scalability. Phys. Rev. B 97, 241401 (2018).
Overhof, H. & Gerstmann, U. Ab initio calculation of hyperfine and superhyperfine interactions for shallow donors in semiconductors. Phys. Rev. Lett. 92, 087602 (2004).
Bethin, J., Castner, T. G. & Lee, N. K. Polarizabilities of shallow donors in silicon. Solid State Commun. 14, 1321–1324 (1974).
Masumi, T. Unified treatment of dielectric enhancement and conduction-electron screening in the Mott transition in semiconductors. Phys. Rev. B 17, 3996–4003 (1978).
Ristic, S., Prijic, A. & Prijic, Z. Dependance of static dielectric constant of silicon on resistivity at room temperature. Serb. J. Electr. Eng. 1, 237–247 (2004).
Dhar, S. & Marshak, A. H. Static dielectric constant of heavily doped semiconductors. Solid-State Electron. 28, 763–766 (1985).
Polley, C. M. et al. Exploring the limits of N-type ultra-shallow junction formation. ACS Nano 7, 5499–5505 (2013).
Suzuki, K. et al. Maximum active concentration of ion-implanted phosphorus during solid-phase epitaxial recrystallization. IEEE Trans. Electron Devices 54, 1985–1993 (2007).
Luisier, M., Schenk, A. & Fichtner, A. W. Full-band atomistic study of source-to-drain tunneling in Si nanowire transistors. In Simulation of Semiconductor Processes and Devices 221–224 (2007).
Ilatikhameneh, H. et al. Tunnel field-effect transistors in 2-D transition metal dichalcogenide materials. IEEE J. Explor. Solid-State Comput. Devices Circuits 1, 12–18 (2015).
Chen, C. et al. Channel thickness optimization for ultrathin and 2-D chemically doped TFETs. IEEE Trans. Electron Devices 65, 4614–4621 (2018).
Polley, C. M. et al. Microscopic four-point-probe resistivity measurements of shallow, high density doping layers in silicon. Appl. Phys. Lett. 101, 262105 (2012).
Hsueh, Y. L. et al. Spin-lattice relaxation times of single donors and donor clusters in silicon. Phys. Rev. Lett. 113, 246406 (2014).
Jensen, B. N. et al. Design and performance of a spherical grating monochromator used at MAX I. Nucl. Instrum. Methods Phys. Res. A 394, 243–250 (1997).
Acknowledgements
J.W.W. acknowledges useful discussions with Prof. Jacob Linder and Dr. Simon Cooil. This work was partly supported by the Research Council of Norway through its Centres of Excellence funding scheme, Project Number 262633, ‘QuSpin’, and through the Fripro program, Project Numbers 250985 ‘FunTopoMat’, 262339 ‘NEAT’, and by the Villum Fonden through the Centre of Excellence for Dirac Materials (Grant No. 11744). J.A.M. acknowledges funding support from the Danish Council for Independent Research, Natural Sciences under the Sapere Aude program (Grant No. DFF-6108-00409) and the Aarhus University Research Foundation. P.D.C.K. acknowledges financial support from The Royal Society.
Author information
Authors and Affiliations
Contributions
F.M., X.-G.Z., C.M.P., T.B., J.A.M., and J.W.W. contributed to the data acquisition. F.M., J.A.M., and J.W.W. analysed the data. C.-Y.C. and R.R. carried out the calculations. F.M., T.B., P.D.C.K., P.H., J.A.M., and J.W.W. contributed to the interpretation of the data and calculations. All authors were involved in the drafting and final approval of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mazzola, F., Chen, CY., Rahman, R. et al. The sub-band structure of atomically sharp dopant profiles in silicon. npj Quantum Mater. 5, 34 (2020). https://doi.org/10.1038/s41535-020-0237-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0237-1
This article is cited by
-
Uncovering anisotropic effects of electric high-moment dipoles on the tunneling current in \(\delta\)-layer tunnel junctions
Scientific Reports (2023)
-
Revealing quantum effects in highly conductive δ-layer systems
Communications Physics (2021)