Abstract
The recent discovery of Sr-doped infinite-layer nickelate NdNiO2 offers a new platform for investigating unconventional superconductivity in nickelate-based compounds. Most intriguingly, the resistivity minimum and Hall coefficient drop were identified simultaneously in the experiment, reflecting a novel electronic structure and transport property of NdNiO2. Driven by this pioneering work, we present a first-principles calculation for the electronic and magnetic structure of undoped parent NdNiO2. By taking into account experimentally relevant interaction strength, we found that (π, π, π) antiferromagnetic NdNiO2 is a compensated bad metal with small Fermi pockets. However, due to the small exchange coupling between 3d-electrons of Ni and strong hybridization with 5d-electrons of Nd, the discovered antiferromagnetic ordering is very weak. Crucially, with the decreasing of temperature, there exists a phase transition between good paramagnetic metal and bad AFM metal. The estimated transition temperature is ~70–90 K, which is consistent with that for observing the resistivity minimum and Hall coefficient drop. In this regarding, our results provide a plausible physical interpretation for these significant experimental observations.
Similar content being viewed by others
Introduction
Since the discovery of high-temperature (high-Tc) superconductivity in cuprates1, extensive effort has been devoted to investigate unconventional superconductors, ranging from non-oxide compounds2,3 to iron-based materials4,5. Exploring high-Tc materials could provide a new platform to understand the fundamental physics behind high-Tc phenomenon, thus is quite valuable. Very recently, the discovery of superconductivity in Sr-doped NdNiO26 potentially raises the possibility to realize high-Tc in nickelate family7,8.
One key experimental observation for the infinite-layer NdNiO2 is that its resistivity exhibits a minimum ~70 K and an upturn at a lower temperature6. At the same time that the resistivity reaches minimum, the Hall coefficient drops towards a large value, signaling the loss of charge carriers6. Interestingly, no long-range magnetic order has been observed in powder neutron diffraction on NdNiO2 when temperature is down to 1.7 K6. This greatly challenges the existing theories, since it is generally believed that magnetism holds the key to understand unconventional superconductivity9,10,11,12. Therefore, it is highly desirable to study the magnetic properties of undoped parent NdNiO2 and elucidate its experimental indications.
In this work, the electronic and magnetic properties of NdNiO2 are systemically studied by first-principles calculations combined with classical Monte Carlo (MC) calculations. For the paramagnetic (PM) phase, its Fermi surface includes one large sheet and two electron pockets at Γ and A point, respectively. This can be approximately described by a three-band low-energy effective model that captures the main physics of exchange coupling mechanism, which is in line with previous works13,14,15,16,17,18. Moreover, by including the Hubbard-U, (π, π, π) anti-ferromagnetic (AFM) ordering is confirmed to be the magnetic ground state. Most significantly, the Fermi surface of AFM phase is simpler than that of PM phase, demonstrating an interaction induced elimination of Fermi pockets. Before NdNiO2 enters correlated insulator, it is a compensated metal with one small electron pocket formed by dxy orbital of Nd and four small hole pockets formed by \({d}_{{z}^{2}}\) orbital of Ni. The estimated phase transition temperature (TN) from PM phase to (π, π, π) AFM phase is ~70–90 K for moderate interaction strength of U = 5–6 eV. Through these studies, our results provide a physical understanding of two experimental observations. First, 3d-electrons of Ni tend to form AFM ordering ~70–90 K, coinciding with the minimum in resistivity and drop in Hall coefficient. Second, the (π, π, π) AFM ordering could be weak (compared with cuprates), because of small effective exchange coupling and strong hybridization with itinerant 5d-electrons of Nd. This could be the reason why AFM ordering is missing in previous studies, which calls for more careful neutron scattering measurements on NdNiO2.
Results
Electronic structure in PM phase
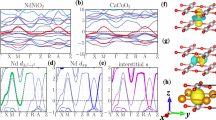
Firstly, we present the band structure of PM phase without Hubbard U. The orbital resolved band structure of PM phase is shown in Fig. 1b. Comparing with typical cuprates CaCuO213, two significant differences are noted: (1) there is a gap ~2.5 eV between 2p orbitals of O and 3d orbitals of Ni. According to Zaanen–Sawatzky–Allen classification scheme19, this indicates that the physics of NdNiO2 is close to Mott-Hubbard rather than charge-transfer13,20,21; (2) there are two bands crossing the Fermi level, in which one is mainly contributed by \({d}_{{x}^{2}-{y}^{2}}\) orbital of Ni (called pure-band) and the other one has a complicated orbital compositions (called mixed-band). In kz = 0 plane, the mixed-band is mainly contributed by \({d}_{{z}^{2}}\) orbital of Nd and Ni. The dispersion around Γ point is relatively small, and the pocket at Γ point is called heavy electron pocket (HEP). In kz = 0.5 plane, the mixed-band is mainly contributed by dxy (dxz, dyz, and \({d}_{{z}^{2}}\)) orbital of Nd (Ni). The dispersion around A point is relatively large, and the pocket at A point is called light electron pocket (LEP). As a comparison, one notices that there is only one pure-band crossing the Fermi level in CaCuO213. The Fermi surface of PM phase is shown in Fig. 1c. There is a large sheet contributed by the pure-band, as the case in CaCuO213. This Fermi surface is obviously two-dimensional (2D), because of the weak dispersion along Γ-Z. In addition, there are two electron pockets residing at Γ and A point, respectively, showing a feature of three-dimensional (3D) rather than 2D (see labels HEP and LEP in Fig. 1(c)). Therefore, the 3D metallic state will be hybridized with the 2D correlated state in NiO2 plane, suggesting NdNiO2 to be an “oxide-intermetalic” compound20,22.
a Atomic structure of tetragonal NdNiO2 and first Brillouin zone. The red and blue lines (labels) denotes the first Brillouin zone of PM phase and (π, π, π) AFM phase, respectively. The high symmetric line for band calculation are Γ(0, 0, 0)-X(0.5, 0, 0)-M(0.5, 0.5, 0)-Γ-Z(0, 0, 0.5)-R(0.5, 0, 0.5)-A(0.5, 0.5, 0.5)-Z. b Orbital resolved band structure of PM phase. The dxy, \({d}_{{z}^{2}}\), dxz+yz, and \({d}_{{x}^{2}-{y}^{2}}\) of Nd (spin-up Ni, spin-down Ni) are marked by black, red, blue, and pick-filled circles. The pz and px+y of O are marked by red, blue, and pick filled circles. The size of circles represents the orbital weights. c Perspective view of Fermi surfaces. LEP and HEP denotes light and heavy electron pocket, respectively. d The comparison between first-principles and Wannier-fitting bands around the Fermi-level. e Top and side view of three maximally localized Wannier functions.
The existence of mixed-band also reflects the inherent interactions between Nd 5d and Ni 3d electrons. To explore the low-energy physics of NdNiO2, a three-band model consisting of Ni \({d}_{{x}^{2}-{y}^{2}}\), Nd \({d}_{{z}^{2}}\) and Nd dxy orbitals is constructed by Wannier90 package. As shown Fig. 1d, one can see the good agreement between first-principles and Wannier-fitting bands near the Fermi level. The little deviation between DFT and Wannier-fitting bands above the Fermi level between Z and R is due to the hybridization between Nd 5d and Ni 3d orbitals. Such a hybridization causes the gap open which is missing in Wannier-fitting bands. The corresponding three maximally localized WFs are shown in Fig. 1e, demonstrating the main feature of \({d}_{{z}^{2}}\) (WF1) and dxy (WF2) orbital of Nd, and \({d}_{{x}^{2}-{y}^{2}}\) (WF3) orbital of Ni. However, these WFs still have some deviations from standard atomic orbitals, that is, WF1 and WF2 are mixed with \({d}_{{z}^{2}}\) orbital of Ni, and WF3 is mixed with px/y orbital of O in the NiO2 plane. According to the classical Goodenough–Kanamori–Anderson rules23,24,25, these deviations (or hybridizations) will give clues for the magnetic properties.
Magnetic properties
To determine the magnetic ground state of NdNiO2, six collinear spin configurations are taken into account in a 2 × 2 × 2 supercell, that is, AFM1 with q = (π, π, π), AFM2 with q = (π, π, 0), AFM3 with q = (0, 0, π), AFM4 with q = (π, 0, 0), AFM5 with q = (π, 0, π), and FM with q = (0, 0, 0), as shown in Fig. 2a. Within all Hubbard U ranges, we found that AFM1 configuration always has the lowest energy, as shown in Fig. 2b, indicating a stable (π, π, π) AFM phase with respect to electron–electron interactions and is in accordance with random phase approximation treatment16. This can be attributed to the special orbital distributions around the Fermi level. The intralayer NN exchange coupling is the typical 180∘ typed Ni–O–Ni superexchange coupling, that is, the coupling between \({d}_{{x}^{2}-{y}^{2}}\) orbital of Ni is mediated by px/y orbital of O (see WF3), preferring a (π, π) AFM phase in NiO2 plane. The interlayer NN exchange coupling is due to the superexchange between the Ni \({d}_{{z}^{2}}\) orbitals mediated by Nd \({d}_{{z}^{2}}\) orbital as shown in WF1, preferring a (π, π) AFM phase between NiO2 planes. Therefore, the superexchange coupling results in a stable (π, π, π) AFM phase in NdNiO2. Moreover, the noncollinear magnetic states are further checked by including the spin-orbit coupling (SOC). We found that the spin moment prefers along c direction with the magnetic anisotropic energy of ~0.5 meV/Ni. Thus, the tiny SOC effect can be safely neglected and the collinear magnetic states are used in the following phase transition temperature calculations.
a Illustration of six collinear spin configurations. The while and black ball represents local up and down spin moment, respectively. The four exchange coupling parameters are indicated by the blue arrows. b Energy comparison for the six collinear spin configurations with different values of Hubbard U. Energy of (π, π, π) AFM is set to zero.
In cuprates, the Fermi surface is unstable with electron–electron interactions, making its parent phase to be an AFM insulator. However, this is apparently not the case in NdNiO2, because of the extra electron pockets and the inherent interaction between Nd 5d and Ni 3d electrons. At U = 0 eV, there are two electron pockets at Γ point and two hole pockets along X–R direction as shown in Fig. 3a, b. Physically, the origin of these four pockets can be easily understood through the comparison of orbital resolved band structures between PM phase (Fig. 1b) and (π, π, π) AFM phase (Fig. 4). Because of the Zeeman field on Ni, its spin-up and -down bands are split away from each other. The original pure-band (\({d}_{{x}^{2}-{y}^{2}}\) orbital of Ni) in PM phase becomes partially occupied in spin-up channel (forming two hole pockets) and totally unoccupied in spin-down channel. Hence, the two hole pockets in AFM phase are inherited from large sheet in PM phase, showing a 2D character with negligible dispersion along Γ–Z direction. For the electron pockets at Γ point, the heavier one is mainly contributed by \({d}_{{z}^{2}}\) orbital of Nd and Ni, so it comes from the HEP at Γ point of PM phase. While for the lighter one, it comes from the LEP at A point of PM phase which is folded into the Γ point of (π, π, π) AFM phase [see Fig. 1a]. The orbital composition can also be used to check this folded band, which is contributed by dxy orbital of Nd, dxz/yz (\({d}_{{z}^{2}}\)) orbital of spin-down (-up) Ni.
a Band structures of (π, π, π) AFM phase with different values of Hubbard U. b–e Perspective view of the Fermi surfaces of (π, π, π) AFM with U = 0, 2, 4, and 6 eV. The two hole pockets in b–d are degenerated and can not be distinguished from this picture. The high symmetry k-points in e are labeled to guide the eye. f Schematic diagram of major self-doping channel at U = 0 and U = 6 eV. The red/blue color represents d orbital of Nd/Ni respectively.
The first, second, third, and forth row represents Nd, spin-up Ni, spin-down Ni, and O, respectively. The filled circles with different colors have the same meaning as those in Fig. 1. The name of d orbitals in the AFM supercell has been aligned to that of unit cell.
These pockets have a different evolution with the increasing value of Hubbard U. For electron pockets, the heavier one is very sensitive to Hubbard U and disappears at U = 1 eV. Meanwhile the lighter one does not disappear until U = 6 eV. In addition, the orbital components of lighter electron pockets are purified by electron–electron interaction and it is mainly contributed by dxy of Nd in the large U limit as shown in Fig. 4. The case for hole pockets is rather complicated. Firstly, the bands of hole pockets become flat with the increasing value of Hubbard U. Secondly, the original hole pockets formed by \({d}_{{x}^{2}-{y}^{2}}\) orbital of Ni gradually disappear, meanwhile, a new hole pocket formed by \({d}_{{z}^{2}}\) orbital of Ni appears along Γ–M as shown in Fig. 3d. At U = 6 eV, NdNiO2 is a compensated metal with a small electron pocket at Γ point and four hole pockets along Γ–M as displayed in Fig. 3e. Further increasing the value of Hubbard U, the system enters an AFM insulator, just like cuprates. Therefore, the metal-to-insulator phase transition point is near U ~ 6 eV. If Hubbard U is <6 eV, NdNiO2 is an AFM metal with relatively small amount of holes that are self-doped16,17,18,20,26 into d orbitals of Ni. Interestingly, there is an orbital switching from \(3{d}_{{x}^{2}-{y}^{2}}\) orbital of Ni at U = 0 eV to \(3{d}_{{z}^{2}}\) orbital of Ni at U = 6 eV in the NiO2 plane, as depicted in Fig. 3f. We speculate that this orbital switching may change the paradigm after doping8,27,28,29,30. Moreover, without the Hubbard U, the 2p orbital of O is far away from the Fermi level, just like the case of PM phase. However, with the increasing value of Hubbard U, the gap between 3d orbital of Ni and 2p orbital of O gradually decreases (Fig. 4), demonstrating an evolution from Mott-Hubbard metal to charge-transfer insulator.
For the magnetic ground state, so far, no consensus has been reached. For example, most of studies assumed the (π, π, 0) AFM order as the ground state, without a detailed energetic investigation, e.g. Gu et al.22, Botana et al.13, and Lee et al.8. Addtionally, Zhang et al.31 and Hepting et al.20 calculated band structures based on (π, π, π) AFM order. Most importantly, the detailed analysis of magnetic ground state is missing in all previous works. In this work, we compare a large number of magnetic configurations and found (π, π, π) (rather than (π, π, 0)) to be the magnetic ground state.
PM-AFM transition
In order to quantitatively describe such a phenomenon, the phase transition temperature is further calculated. For (π, π, π) AFM phase, the magnetic momentum of Ni increases from 0.58 μB (U = 0 eV) to 1.04 μB (U = 8 eV) and becomes gradually saturated, as shown in Fig. 5a. This is also consistent with the fact that \({d}_{{x}^{2}-{y}^{2}}\) orbital of Ni is closer to single occupation with the increasing value of Hubbard U. Therefore, Ni is spin one half (S = 1/2) in infinite-layer NdNiO2, just like the case in cuprates. To extract the exchange coupling parameters of J1, J2, J3, and J4 (as labeled in Fig. 2a), the total energy of five AFM configurations obtained from DFT + U calculations are mapped onto the Heisenberg spin Hamiltonian. In the 2 × 2 × 2 supercell, there are 8 Ni atoms and the total energy of different AFM configurations are:
where E0 is the reference energy without magnetic order. Only (π, π, π) and (π, π, 0) are stable at U = 0 eV, and we ignore results at U = 0 eV in the following discussions. The calculated exchange coupling parameters as a function of Hubbard U are shown in Fig. 5b. We would like to make several remarks here: (1) the NN intralayer exchange coupling (J1), mediated by \({d}_{{x}^{2}-{y}^{2}}\) orbital of Ni, demonstrates a 1/U law; (2) the NN interlayer exchange coupling (J2) is ~10 meV with little variation. The positive value of J2 indicates an AFM coupling between NiO2 planes; (3) the next NN intralayer exchange coupling (J3), mediated by dxy orbital of Nd, is comparable to J1 at large value of Hubbard U, which is dramatically different to that in infinite-layer SrFeO232,33,34. This large value could be attributed to the relative robustness of lighter electron pocket and orbital purification; (4) the next NN interlayer exchange coupling (J4) is ~0 meV, indicating the validity of our Hamiltonian up to the third NN; (5) J1, J2, and J3 have the same strength at large U, suggesting NdNiO2 is a 3D magnet rather than 2D magnet.
The Hubbard U dependence of a the magnetic momentum of Ni in (π, π, π) AFM phase, b the exchange coupling parameters, c specific heat (C) vs T with four J's, d the estimated TN with four J's, e specific heat C vs T with J1, J3 only and f the estimated TN with J1, J3 only. The shaded region in d highlights the possible TN of 70–90 K with a reasonable U = 5–6 eV.
Based on the above exchange coupling parameters, the phase transition temperature (TN) is calculated by classical Monte Carlo method in a 12 × 12 × 12 supercell based on the classical spin Hamiltonian:
where the spin exchange parameters Jij have been defined above. First, we calculate the specific heat (C) after the system reaches equilibrium at a each given temperature (T), as shown in Fig. 5c. Then, T is extracted from the peak position in the curve of C(T), as shown in Fig. 5c. For U = 1 eV, TN is as high as 220 K, which can be ascribed to the large value of J1. With the increasing value of Hubbard U, TN gradually decreases and becomes ~70 K at U = 6 eV. To further check the effect of interlayer exchange coupling on 3D magnet, an additional Monte Carlo calculation is performed without J2 and J4. As shown in Fig. 5e, the C(T) vs C(T) plot shows a broaden peak at a lower temperature. Since Mermin-Wagner theorem prohibit magnetic order in 2D isotropic Heisenberg model at any nonzero temperatures35, the broad peak in C(T) vs T plot implies the presence of short-range order. Regarding the small drop of TN (~30 K in Fig. 5f), our MC simulations indicate that the weak interactions between NiO2 planes.
Experimental relevance
To address the relevance of the current calculations and experimental observations, we first estimate the value of Hubbard interaction strength U. Although the exact value of Hubbard U cannot be directly extracted from the first-principles calculations, its value range can still be estimated based on similar compounds. The infinite-layer nickelate is believed to be a worse metal compared to elemental nickel with U ~ 3 eV36, which can be considered as a lower bound of Hubbard U. The Coulomb interaction in infinite-layer nickelates should be smaller than that in the charge-transfer insulator NiO with U ~ 8 eV37, which can be considered as a upper bound of Hubbard U. Therefore, a reasonable value of Hubbard U in NdNiO2 will be between 3 eV and 8 eV. In the following discussion, we would like to use the median value, U ~ 5–6 eV.
Second, if the interaction strength is around U ~ 5–6 eV, the estimated magnetic exchange interaction is around J1 ~ 10 meV, J2 ~ 10 meV, J3 ~ −13 meV (see Fig. 5b). This indicates that, effective exchange interactions in NdNiO2 are about one-order smaller than those of cuprates ~112 meV21,38,39,40,41,42,43,44. Also it results in a relative weaker magnetic ordering and lower Neel temperature TN in NdNiO2, compared with cuprates (see below).
Third, to further discuss the magnetic transition temperature, we show the Neel temperature dependence on interaction strength in Fig. 5d. Within the estimated interaction range U ~ 5–6 eV, we find the Neel temperature, which separates the PM phase from the (π, π, π) AFM phase, is near 70–90 K. Interestingly, this coincides with the minimum in resistivity and the drop in Hall coefficient6. It provides a novel understanding of minimum in resistivity, i.e. partial electrons tend to localize and form magnetic order, therefore the conducting carriers decreases. Thus, our calculation indicates that, the resistivity minimum and the drop in Hall coefficient relates to the magnetic phase transition at the Neel temperature.
Fourth, previous power neutron scattering measurement on NdNiO2 did not find the signal of AFM ordering45,46. This could be attributed to the following reason. The estimation of Neel temperature (in Fig. 5d) does not include the influence of conduction electrons. We notice that, there are small Nd 5d-electron pockets near the Fermi surface at the critical interaction strength (Fig. 3e). By concluding the hybridization effect between Nd 5d-electrons and Ni 3d-electrons, there are at least two influences. On one hand, it is expected that the local magnetic AFM ordering below the Neel temperature is further weakened. On the other hand, the magnetic phase transition is replaced by a crossover from normal metal to bad AFM metal around TN ~ 70–90 K, which is more likely to occur in the experiment6. Both of the above effects lead to further weaken the AFM ordering26, which could be hard to detect in neutron scattering measurement.
Lastly, some recent experiments fail to find bulk superconductivity in NdNiO2 systems, and the parent samples show strong insulating behaviors47. The insulating behavior could be attributed to strong inhomogenious disorder or improper introduction of H during the reaction with CaH248. Especially, it is worth noting, these experiments cannot rule out the possibility of weak AFM ordering, due to the presence of Ni impurities in their samples. (Actually this problem has been pointed out before45,46.) The strong ferromagnetic order from elemental Ni would dominate over and wash out the weak signal of AFM ordering from NdNiO2 as we suggested in this work.
Taken as a whole, we conclude that, our calculations provide a self-consistent understanding on the experimental observation6: the resistivity minimum and drop in Hall coefficient is related to the crossover from normal metal to bad AFM metal around TN ~ 70–90 K. The AFM ordering at lower temperature is weak due to the hybridization or self-doping effect, which is hard to detect in the previous measurements. In this regarding, the upcoming inelastic neutron scattering on high-quality samples is highly desired.
Discussion
In this work, we present a systematic study of the electronic and magnetic properties of parent compound NdNiO2 by first-principles calculations combined with classical Monte Carlo calculations. The Fermi surface of PM phase is quite large with two 3D-liked electron pockets, which is consistent with the previous work13,14,15,16,18. By tuning the interaction strength, before it enters correlated insulator, NdNiO2 is a compensated metal with one small electron pocket formed by dxy orbital of Nd and four small hole pockets formed by \({d}_{{z}^{2}}\) orbital of Ni. We identify the interaction selects a (π, π, π) AFM order as the correct magnetic ground state. In the reasonable estimation U = 5–6 eV20,37, we find several conclusions related to the experiment6: (1) the exchange-coupling parameters are ~10 meV, which is one order smaller than cuprates21,38,39,40,41,42,43,44 and results in a low TN compared with cuprates; (2) the self-doing effect from 5d orbital of Nd and 3d orbital of Ni may screen the local magnetic momentum in \({d}_{{x}^{2}-{y}^{2}}\) orbital of Ni, which gives a small magnetic momentum less than 1 μB and makes the long-range AFM order unstable6,45,49,46; (3) with the decreasing of temperature, there is a phase transition from PM phase to (π, π, π) AFM phase near 70–90 K. Therefore, there could exist a transition from normal metal to bad AFM metal around TN ~ 70–90 K, which provides a plausible understanding of minimum of resistivity and Hall coefficient drop in infinite-layer NdNiO26. We envision that our calculations will intrigue intensive interests for studying the magnetic properties of high-quality infinite-layer NdNiO2 samples.
Methods
The first-principles calculations are carried out with the plane wave projector augmented wave method as implemented in the Vienna ab initio simulations package (VASP)50,51,52. The Perdew–Burke–Ernzerhof (PBE) functionals of generalized gradient approximation (GGA) is used for PM phase53. To incorporate the electron-electron interactions, DFT + U is used for AFM phase, which can reproduce correctly the gross features of correlated-electrons in transition metal oxides54,55,56. There are two kinds of strongly localized orbitals in NdNiO2: 4f of Nd and 3d of Ni. The 4f electrons of Nd are expected to display the local magnetic moment as Nd3+ in Nd2CuO457. The hybridization between f electrons and superconducting plane is very complicated. In EuRbFe4As458, superconductivity in FeAs layers and ferromagnetism in Eu layers can coexist. In PrBa2Cu3O7, where the local environment of the 4f ion is the same as in NdNiO2, the antibonding coupling of the Pr \({f}_{z({x}^{2}-{y}^{2})}\) orbital to the O 2p orbitals makes PrBa2Cu3O7 not superconducting59. Recently, it has been proposed that the intra-atomic 4f–5d exchange coupling of Nd may change the understanding of the superconducting properties in NdNiO260. Since the local magnetic moment of Nd3+ is weakly coupled in NdNiO260, here we ignore the possibility of local moment formed by 4f electron of Nd3+ in our calculation by treating them as the core-level electrons and focus only on the magnetic order fromed by Ni. The Hubbard U (0–8 eV) term is added to 3d electrons of Ni. The energy cutoff of 600 eV, and Monkhorst-Pack k point mesh of 11 × 11 × 11 and 18 × 18 × 30 is used for PM and AFM phase, respectively. The maximally localized Wannier functions (WFs) are constructed by using Wannier90 package61,62. The structure of infinite-layer NdNiO2 is shown in Fig. 1a, including NiO2 layers sandwiched by Nd, which can be obtained from the perovskite NdNiO3 with reduction of apical O atoms in c direction45,46. Due to apical O vacancies, the lattice constant in c direction shrinks (smaller than a direction) and the space group becomes P4/mmm. The experimental lattice constant a = b = 3.92 Å and c = 3.28 Å are used in our calculations.
Data availability
The numerical datasets used in the analysis in this study, and in the figures of this work, are available from the corresponding author on reasonable request.
References
Bednorz, J. G. & Müller, K. A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B. 64, 189–193 (1986).
Nagamatsu, J., Nakagawa, N., Muranaka, T., Zenitani, Y. & Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 410, 63–64 (2001).
Drozdov, A. P., Eremets, M. I., Troyan, I. A., Ksenofontov., V. & Shylin, S. I. Conventional superconductivity at 203 kelvin at high perssures in the sulfur hydride system. Nature 525, 73–76 (2015).
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Iron-based layered superconductor La(O1−XFx)FeAs(x = 0.05 − 0.12) with Tc = 26 K. J. Am. Chem. Soc. 130, 3296–3297 (2008).
Wang, Q.-Y. et al. Interface-Induced high-temperature superconductivity in single unit-cell FeSe films. Chin. Phys. Lett. 29, 037402 (2012).
Li, D. et al. Superconductivity in an infinite-layer nickelate. Nature 572, 624–627 (2019).
Anisimov, V. I., Bukhvalov, D. & Rice, T. M. Electronic structure of possible nickelate analogs to the cuprates. Phys. Rev. B 59, 7901–7906 (1999).
Lee, K.-W. & Pickett, W. E. Infinite-layer LaNiO2 : Ni1+ is not Cu2+. Phys. Rev. B 70, 165109 (2004).
Patrick, A. L., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Dai, P., Hu, J. & Dagotto, E. Magnetism and its microscopic origin in iron-based high-temperature superconductors. Nat. Phys. 8, 709–718 (2012).
Dai, P. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896 (2015).
Botana, A. S. & Norman, M. R. Similarities and differences between infinite-layer nickelates and cuprates and implications for superconductivity. Phys. Rev. X 10, 011024 (2020).
Jiang, P.-H., Si, L., Liao, Z. & Zhong, Z.-C. Eletronic structure of rare-earth infinite-layer RNiO2 (R=La, Nd). Phys. Rev. B 100, 201106 (2019).
Gao, J.-C., Wang, Z.-J., Fang, C. & Weng, H.-M. Electronic structures and topological properties in nickelates \({{\rm{Ln}}}_{{\rm{n+1}}}{{\rm{Ni}}}_{{\rm{n}}}{{\rm{O}}}_{2{\rm{n}}+2}\). Preprint at https://arxiv.org/abs/1909.04657 (2019).
Wu, X. et al. Robust \({d}_{{x}^{2}-{y}^{2}}\)-wave superconductivity of infinite-layer nickelates. Phys. Rev. B 101, 060504 (2020).
Nomura, Y. et al. Formation of 2D single-component correlated electron system and band engineering in the nickelate superconductivity NdNiO2. Phys. Rev. B. 100, 205138 (2019).
Sakakibara, H. et al. Model construction and a possibility of cuprate-like pairing in a new d9 nickelate superconductor (Nd, Sr)NiO2. Preprint at https://arxiv.org/abs/1909.00060 (2019).
Zaanen, J., Sawatzky, G. A. & Allen, J. W. Band gaps and electronic structure of transition-metal compounds. Phys. Rev. Lett. 55, 418–421 (1985).
Hepting, M. et al. Electronic structure of the parent compound of superconducting infinite-layer nickelates. Nat. Mater. 19, 387–385 (2020).
Jiang, M., Berciu, M. & Sawatzky, G.A. The critical nature of the Ni spin state in doped NdNiO2. Priprint at https://arxiv.org/abs/1909.02557 (2019).
Gu, Y., Zhu, S., Wang, X., HuJ. & Chen, H. Hybridization and correlation effects in the electronic structure of infinite-layer nickelates. Preprint at https://arxiv.org/abs/1911.00814 (2019).
Goodenough, J. B. Theory of the role of covalence in the perovskite-type manganites [La, M(II)]MnO3. Phys. Rev. 100, 564 (1955).
Anderson, P. W. New approach to the theory of superexchange interactions. Phys. Rev. 115, 2 (1959).
Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 10, 87–89 (1959).
Zhang, G.-M., Yang, Y.-F. & Zhang, F.-C. Self-doped Mott insulator for parent compounds of nickelate superconductors. Phys. Rev. B 101, 020501 (2020).
Lechermann, F. Late transition-metal oxides with infinite-layer structure: nickelate vs. cuprate. Phys. Rev. B 101, 081110 (2020).
Zhang, Y.-H. & Vishwanath, A. Type II t-J model in superconducting nickelate Nd1−xSrxNiO2. Priprint at https://arxiv.org/abs/1909.12865 (2019).
Werner, P. & Hoshino, S. Nickel superconductors - multiorbital nature and spin freezing. Phys. Rev. B 101, 041104 (2020).
Hu, L.-H. & Wu, C. Two-band model for magnetism and superconductivity in nickelates. Phys. Rev. Res. 1, 032046 (2019).
Zhang, H. et al. Effective Hamiltonian for nickelate oxides Nd1−xSrxNiO2. Phys. Rev. Res. 2, 013214 (2020).
Tsujimoto, Y. et al. Infinite-layer iron oxide with a square-planar coordinate. Nature 450, 1062 (2007).
Hayward, M. A. & Rosseinsky, M. J. Materials chemistry: cool conditions for mobile ions. Nature 450, 960 (2007).
Xiang, H. J., Wei, S.-H. & Whangbo, M.-H. Origin of the structural and magnetic anomalies of the layered compound SeFeO2 : a density functional investigation. Phys. Rev. Lett. 100, 167207 (2008).
Mermin, N. D. & Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 100, 1133–1136 (1966).
Aryasetiawan, F., Karlsson, K., Jepsen, O. & Schönberger, U. Calculations of Hubbard U from first-principles. Phys. Rev. B 74, 125106 (2006).
Cococcioni, M. & de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA + U method. Phys. Rev. B 17, 1133 (1966).
Bourges, P., Casalta, H., Ivanov, A. S. & Petitgrand, D. Exchange coupling and spin susceptibility spectral weight in undoped monolayer cuprates. Phys. Rev. Lett. 79, 4906 (1997).
Coldea, R. et al. Spin waves and electronic interactions in La2CuO4. Phys. Rev. Lett. 86, 5377 (2001).
Braicovich, L. et al. Dispersion of magnetic excitations in the cuprate La2CuO4 and CaCuO2 compounds measured using resonant X-Ray scattering. Phys. Rev. Lett. 102, 167401 (2009).
Blumberg, G. et al. Two-magnon Raman scattering in cuprate superconductors: evolution of magnetic fluctuations with doping. Phys. Rev. B 49, 13295 (1994).
Blumberg, G. et al. Resonant two-magnon Raman scattering in cuprate antiferromagnetic insulators. Phys. Rev. B 53, R11930 (1996).
Ryee, S. et al. Induced magnetic two-dimensionality by hole doping in superconducting Nd1−xSrxNiO2. Phys. Rev. B 101, 064513 (2020).
Wan, X., Maier, T. A. & Savrasov, S. Y. Calculated magnetic exchange interactions in high-temperature superconductors. Phys. Rev. B 79, 155114 (2009).
Hayward, M. A., Green, M. A., Rosseinsky, M. J. & Sloan, J. Sodium hydride as a powerful reducing agent for topotactic oxide deintercalation: synthesis and characterization of the nickle(I) oxide LaNiO2. J. Am. Chem. Soc. 121, 8843–8854 (1999).
Hayward, M. A. & Rosseinsky, M. J. Synthesis of the infinite layer Ni(I) phase NdNiO2+x by low temperature reduction of NdNiO3 with sodium hydride. Solid State Sci. 5, 839–850 (2003).
Li, Q. et al. Absence of superconductivity in bulk Nd1−xSrxNiO2. Comms. Mater. 1, 16 (2020).
Si, L.et al. Topotactic hydrogen in nickelate superconductors and akin infinite-layer oxides ABO2. Preprint at https://arxiv.org/abs/1911.06917 (2019).
Fu, Y.et al. Electronic structures and spin fluctuations in nickelate oxide NdNiO2. Preprint at https://arxiv.org/abs/1911.03177 (2019).
Teter, M. P., Payne, M. C. & Allan, D. C. Solution of Schrödinger’s equation for large systems. Phys. Rev. B 40, 12255 (1989).
Kresse, G. & Furthmüller, J. Effective iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Anisimov, V. I., Zaanen, J. & Anderson, O. K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 44, 943–954 (1991).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study. Phys. Rev. B 57, 1505 (1998).
Rohrbach, A., Hafner, J. & Kresse, G. Electronic correlation effects in transition-metal sulfides. J. Phys.: Condens. Matter 15, 979–996 (2003).
Casalta, H., Bourges, P., d’Astuto, M., Petitgrand, D. & Ivanov, A. Magnetic behavior of Nd in Nd2CuO4 above 1.5 K. Phys. Rev. B 57, 471–475 (1998).
Liu, Y. et al. Superconductivity and ferromagnetism in hole-doped EuRbFe4As4. Phys. Rev. B 93, 214503 (2016).
Liechtenstein, A. I. & Mazin, I. I. Quantitative model for the superconductivity suppression in R1−xPrxBa2Cu3O7 with different rare earths. Phys. Rev. Lett. 74, 1000–1003 (1995).
Choi, M.Y., Lee, K.-W. & Pickett, W.E. Pickett, W. E. Role of 4f states in infinite-layer NdNiO2. arXiv pre-print 1911.02999 (2019).
Mostofi, A. A. et al. Wannier90: a tool for obtaining maximally-localized Wannier functions. Comput. Phys. Commun. 178, 685 (2008).
Marzari, N., Mostofi, A. A., Yats, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: theory and applications. Rev. Mod. Phys. 84, 1419–1475 (2012).
Acknowledgements
W.Z. thanks Chao Cao for sharing their unpublished DMFT results, and thanks Filip Ronning, H. H. Wen, G. M. Zhang for helpful discussion. This work was supported by NSFC (No. 11774325, 21603210, 21603205, and 21688102), National Key Research and Development Program of China (No. 2017YFA0204904 and 2016YFA0200604), Anhui Initiative in Quantum Information Technologies (No. AHY090400), Fundamental Research Funds for the Central Universities and the Start-up Funding from Westlake University. We thank Supercomputing Center at USTC for providing the computing resources.
Author information
Authors and Affiliations
Contributions
W.Z. and J.Y. proposed the idea. Z.L. carried out the calculations and drafted the article. All authors contribute to the analysis of date, writing, and revision of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, Z., Ren, Z., Zhu, W. et al. Electronic and magnetic structure of infinite-layer NdNiO2: trace of antiferromagnetic metal. npj Quantum Mater. 5, 31 (2020). https://doi.org/10.1038/s41535-020-0229-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0229-1
This article is cited by
-
Competing incommensurate spin fluctuations and magnetic excitations in infinite-layer nickelate superconductors
Communications Physics (2023)
-
Antiferromagnetic insulating state in layered nickelates at half filling
Scientific Reports (2022)
-
Magnetic and f-electron effects in LaNiO2 and NdNiO2 nickelates with cuprate-like \(3{d}_{{x}^{2}-{y}^{2}}\) band
Communications Physics (2021)
-
Nickelate superconductors—a renaissance of the one-band Hubbard model
npj Quantum Materials (2020)
-
Spin excitations in nickelate superconductors
Science China Physics, Mechanics & Astronomy (2020)